氮化钛居里温度的计算

李军

（西南大学，重庆400715）

早在2004 年，石墨烯就由安德烈·盖姆及其同事通过一种简单的透明胶带剥离方法制备[5-8]，它开启了研究和应用二维（2D）材料的新时代。石墨烯的一些特殊物理特性激发了所有人的研究热情，其中包括出色的光学透明度[12]，很好的电导率和导热率[13]，室温下超高的载流子迁移率[14]和还同时具有量子霍尔效应[15].同时研究人员已经通过实验和理论方法研究新型的二维石墨烯状物质：硅[16][17]，锑[18]和MXene。二维材料拥有者三维材料没有的优势，由于它的新颖的物理性质和化学性质。但是磁性二维材料不是很理想，只有很少的发现。具有双重性质的磁性半导体（铁磁和半导体）很可能会成为一种新型的自旋电子器件。大多数磁性半导体是过渡金属化合物。在最近几年中，已经出现了许多具有各种物理性质并有助于自旋电子学发展的二维过渡金属化合物。例如，具有高自旋极化的半金属单层TMN（TM = Cr，Mn，V）[9][10][11]。这些过渡金属化合物形成单层结构后，过渡金属原子的d 电子轨道是不对称的，从而导致某些独特的物理性质。此外，通过将磁性原子掺杂到没有磁性的半导体中来获得磁性半导体.二维磁性材料可广泛应用于许多领域，其中最有潜力的是自旋电子学领域，而对于该领域来说二维材料的居里温度的计算时非常重要的，也就是研究磁性材料的一个重要的物理性质。所以，我们运用一些方法去计算居里温度是对于我们研究二维材料作为自旋电子学器件必不可少的工作。

1 计算细节

所有原子和电子结构计算均使用密度泛函理论（DFT）[19]中的PBE 中和与HSE06 交换相关的功能完成，并以VASP 代码实现。由于Ti 原子中存在d 轨道电子（考虑到其强相关性），因此使用U（GGA + U）方法进行结构优化。我们应用在Z 方向上的15真空区域可防止层到层相互作用。平面波截断可以设置为500 eV。在结构松弛和电子计算中，11×11×1 布里渊区域使用25×25×1 K 点网格分别使用Monkhorst-Pack 方法进行抽样。能量和力计算的收敛标准设置为10-5eV /atom 和0.01 eV /。

2 计算结果

2.1 结构优化

六角形蜂窝状TiN 单分子层可以通过具有Fm3m 群组结构的块体上进行剥离。结构如图1 所示。 从图中我们可以看到，每个Ti 原子和N 原子之间存在三配位（类似于石墨烯结构），并且具有对称的D3h 点组。 TiN 单层的优化晶格常数为3.885，相应的Ti-N 键长为1.942。

图1

2.2 二维材料居里温度的计算

前面已经提到居里温度是磁性相变温度，这是磁性材料从铁磁性变为顺磁性的临界温度。它是研究磁性材料的重要物理性能。对于我们研究的二维单层材料来说，它在0 K 时具有铁磁基态。为了确定T＞0 K 时二维单层结构的优先磁基态结构，考虑了共线FM和AFM状态。通过将具有不同磁性结构的系统的总能量映射到Ising 模型方法，可以提取最近邻居交换耦合参数J。通常，与最近邻居交换耦合参数相比，可以忽略次近邻居交换耦合和次次近邻居交换。通常情况下，二维材料中产生磁性的原子间的相互作用，只有最近邻原子相互作用最强，其他近邻相互作用比起最近邻的至少弱几个量级，所以对于其他近邻相互作用对于系统的能量的影响微乎其微，所以一般不需要考虑。 Ising 模型用于估计二维单层材料的居里温度的这种用法称为平均场近似理论，运用平均场近似理论可以简化二维单层材料求解居里温度。这种最近邻的自旋相互作用可以近似等于交换耦合参数J，并且可以使用经典的哈密顿量通过自旋系统的总能量来描述二维伊辛模型[1]：

其中，Jij表示两个相邻的i 和j 自旋之间的磁交换耦合常数Si和Sj，和分别是二维真空方向上的平行或反平行自旋。通常，在该各向同性模型中，通过DFT 计算的能量仅需要映射到哈密顿量中，也就是说，可以通过FM 和AFM 自旋排列之间的交换能量来估算交换耦合常数。 根据先前对二维六边形晶体结构的居里温度的计算[1][2][3]，交换耦合常数J 可以表示为：

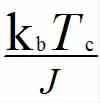
总而言之，计算磁性材料居里温度虽然有很多种方法，平均场近似为既简单又实用的方法，运用这种方法可以较为准确的估测出二维材料的居里温度。上述报告从原理上和从计算方法上探讨了二维材料居里温度的估算。