概率论模型在医疗工作中的应用

杨叶姿

（1、苏州外国语学校，江苏 苏州215011 2、武汉大学 数学与统计学院，湖北 武汉430072）

1 概述

2020 年3 月11 日，世界卫生组织评估：新型传染病可能在2020 年全球大流行[1，2]。在面对传染病问题，我国积累了大量经验，建立统一高效的指挥体系、构建全民参与严密防控体系、全力救治患者、拯救生命、依法及时公开透明发布病情信息，充分发挥科技支撑作用，实现了防控和救治两个战场协同作战，并有效的遏制传染病蔓延势头[3]。

我国虽然在宏观层面对传染病进行了有效控制，但在实际防控措施中，各机构也遇到了许多具体问题，比如：居民防控意识不强、医院的检测方法和治疗方案发展不成熟、科研机构的疫苗研发进展不乐观等[4]。本文将从概率统计的角度，对数据统计不准确、医疗检测效率低、存在误诊风险、疫苗研发的有效性问题建立模型，为提高疫情诊断、治疗效率，提供数学理论依据和改进建议。

2 谎报出行问题的应对

在控制传染疾病的举措中，各地都在进行全体居民出行及接触人群的调查与统计。若能够获得居民出行记录的准确信息，有关部门则可以估计交叉感染风险、无症状携带者信息等，从而对公共场所制定相应的开放措施。但在实际调查中，传染病流行期间出行问题属于敏感或隐私问题，被调查者可能担心出行后会被隔离或限制活动。因此，不排除少量居民隐瞒、谎报出行信息的情况，此行为给防控工作带来了干扰。本节设计一个出行记录敏感问题的调查方案，通过加入混淆的问题来保护被调查者隐私，根据全概率公式[5]，来估计被调查者中谎报出行记录的概率。

2.1 调查问卷的规则设计

根据调查方案的设计原则[6]，对未进行医学检测的居民设计调查问卷，该调查问卷的形式多样，比如自行申报、口头询问或网络问卷等。调查问卷的主要目的是：在出行情况的调查问卷反馈信息中，如何甄别真伪，获得谎报信息的真实情况。

问题规则：设计一个有红黄蓝三种颜色区域的圆盘，该圆盘上有一个可随机指向三种颜色区域的指针。被调查者转动指针随机指向一种颜色，并回答该颜色的对应问题。

（1）红色区域对应的问题：你有过谎报出行记录的行为吗？如果有过，请回答“1”，如果从未有过，请回答“0”；

（2）黄色区域问题：请直接回答“1”；

（3）蓝色区域问题：请直接回答“0”。

被调查者转动指针时，调查者无法看见转动情况，无法判断被调查者回答的是哪个问题。此试验中黄色和蓝色区域存在的意义：混淆调查者对于被调查者所回答问题的判断，以此来保护被调查者的个人信息隐私，消除被调查者心中的顾虑，使调查结果更加准确[7]。

2.2 概率模型

设A1为随机事件“指针指向红色区域”，A2为随机事件“指针指向黄色区域”，A1为随机事件“指针指向蓝色区域”。记P（Ai）=pi，i=1，2，3 该概率由调查者通过调节圆盘各颜色面积事先确定。设B 为事件“回答结果是1”，则由全概率公式得

其中P（B|Ai）表示在回答Ai问题时，回答结果是1 的概率。

不妨设被调查者有n 位，每位均独立作答，回答是“1”的人数为n1，则被调查者中有谎报出行记录的概率为

2.3 模型分析

2.4 数值模拟计算

借助数学工具软件Matlab 的随机生成数功能进行数据模拟分析，假设谎报出行的实际概率为0.005，p3固定为0.2 时，对于不同的p1和p2值，随着被调查者人数的变化，谎报出行记录的概率P（B|A1）都逐渐收敛到真实值0.005，具体如下图。

由第四张图可以发现：当p1越大、p2越小时，P（B|A1）收敛到真实值的速率越快。

2.5 数据验证

不妨将圆盘的颜色比例，设计为p1=0.75，p2=0.075 和p1=0.175。通过实地发放调查问卷，有效的调查结果是：总被调查者6839 人，536 人次回答结果是“1”。由公式（1）可计算出

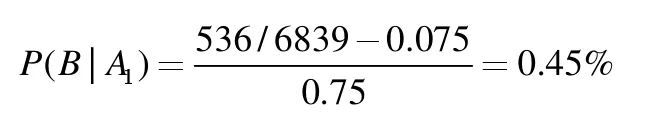
表示人群中谎报出行的概率为0.45%。由这个样本推断谎报出行记录的平均人数为

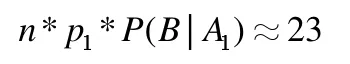
更一般的，假设城市人口总数为N，该城市居民患病率为p，城市中未被隔离/未发现的潜在传染病患者为

数值验证：某市截至2019 年末的常住人口为1121.2 万人[8]。截至2020 年7 月20 日，该市的传染病感染总人数为50340人。根据公式（2）可估算出患病率为p=0.449%。因此，未被隔离的潜在传染病患者的估计人数为

有关政府部门可以根据这个估算结果，来判断关于公共场所的开放程度和城市出行的隔离程度，制定相关措施。例如，若该结果较大，则公共场所应该限制人数并加强体温检测以及对群众佩戴口罩的监督；若该结果较小，则可恢复公共场所的正常运转。

另外在调查时，可以加入对年龄等个人资料的调查，可估算出未被隔离的潜在传染病患者，若低龄者比例很少，则学校可以由线上授课转为线下授课；若中年人比例较低，则可恢复经济活动的线下运转。

3 混合检测方案

在传染病重灾区，政府对全体居民进行医学检测。但由于人数众多，而检测设备的数量和检测速率有限，每一次检测的时间及经济成本大，本文设计了提高群体检测效率方案，即混合样本检测，并通过概率计算比较传统检测方法与本文方案的平均成本以及最佳混合样本数量。

具体方案：将多个人的检测样本混合在一起检测。如果混合的检测样本没有病毒，则这些人都不携带病毒；如果混合的检测样本含有病毒，则这些个人再分别检测，查出含有病毒的那个或那些人。这个方法目的在于减少检测的次数，以减小经济成本，提高检测效率。

设混合样本包含了n 个人的检测样本，每个人的患病率为p。

检测次数 1 1+n 概 率 （1-p）� 1-（1-p）�

E1表示传统检测方案的平均检测次数，E2表示采用混合检测方法的平均检测次数，则

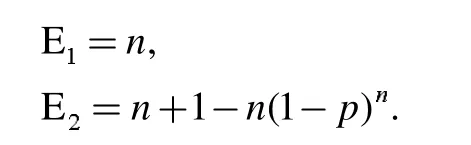
对固定的p，当n 满足n（1-p）n＞1 时，混合检测的平均次数少于传统检测的平均次数。

上图表明：混合方法与传统方法在不同样本量下的平均检测次数，并对比了不同患病率下混合方法应采取的最佳每组样本量。注意到传统方法中，检测次数等于样本量。

建议：当患病率低时，采用混合样本检测的方法检测效率更高。而患病率高时，采用直接检测单个检测样本当效率更高。患病率可以随时根据上一次检测结果来进行调整。除此之外，根据调查研究显示，中老年人相较于青年人和儿童的患病率要高许多[9]，因此，医院在将样本分组时，可以根据年龄段来分组。中老年人可减少每组样本数量，而青年人和儿童组可以增加每组样本数量。

4 降低医院误诊率方案

在医院进行医学检测时，存在一定的误诊率，被误诊的群体会承担巨大经济、心理压力和健康风险，同时，如果医院的检测效率不高，社会群众会感到不安。本节提出了降低医院误诊率方案，即对检测出患病的患者进行二次检测，通过贝叶斯公式和全概率公式计算出前后误诊率的变化，并给出科学建议。

4.1 理论依据

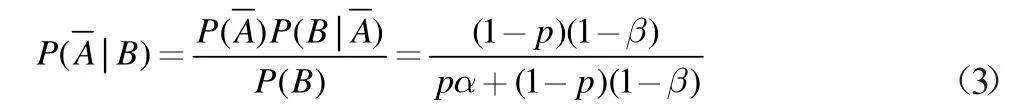
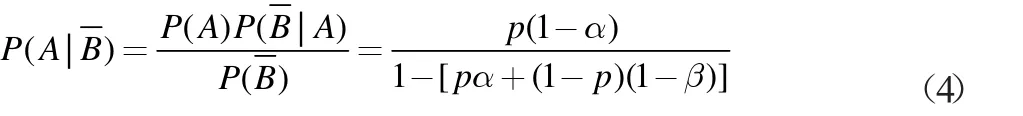
分析可得，当p 取值较小，α 和β 固定时，诊断出患病的人数中，实际不患病的比率很大，且远大于诊断出不患病的人数中实际患病的比率。

危害分析：

（1）对于诊断出患病而实际没有患病的患者来说，他们会承担不必要的压力和风险，因为他们需支付医疗费用，自己与家人也会承担一部分心理压力。其次，如果医院诊断他们患传染病，并将他们与其他传染病患者一起隔离，则本来不患病的人有可能被感染。另外，若医院的医疗资源紧缺，再分配给不患病的人会很浪费。

（2）对于诊断出无病而实际有病的患者来说，如果他们得不到及时的医治，患者会有生命安全的问题。而如果他们不被有效隔离，他们会传染给更多人，加重更多人的负担和风险。

因此，对于传染病来说，降低误诊率非常重要。

改善方法：多次诊断来降低误诊率。由于诊断出患病的人数中，不患病的比率很大，且远大于诊断出不患病的人数中患病的比率，第一次被诊断患病的人进行第二次单独诊断。

理论推导：设Bi为第i 次诊断患病，i=1，2。则两次诊断都是患病的概率

此时，如果两次诊断都是患病，但实际上被检测者未患病的概率为

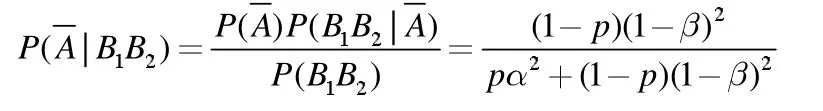
4.2 数值分析

利用2.5 中数据验证的该市患病率p=0.449%，现在医院的检测技术和设备很先进了，不妨取α=0.95，β=0.99，此时被检测者的患病率为P（B）=1.42%

而两次诊断都是患病但被检测者未患病的概率为

由此可见，第一次被检测出患病的群体中，通过二次检测使得被误诊患病的比率，从70%下降到2.398%，降低幅度达到96.57%。对于罕见病例，第一次检测出患病的群体来说，要及时进行第二次复查，可以大大被误诊率。

对于第一次检测结果为患病，第二次检测结果为不患病的人中，

（1）实际不患病的概率为

（2）实际患病的概率为

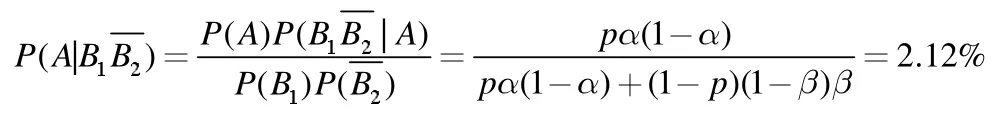
因此，对于第一次诊断结果为患病，第二次诊断结果为不患病的患者，实际情况为不患病的概率更大，所以对于这些人，建议医院的最终诊断为不患病。

4.3 建议

这个方法针对传播率低的疾病。因为第二次诊断时，原本诊断患病而实际患病的人有可能会被误诊，如果这些人不被有效隔离，病毒会扩散传染。对于传播率高的疾病建议第二次诊断第一次没有患病的人，但是这种方法耗费的时间和经济成本很大。所以具体医院采用的方法应结合该医院的误诊率、患病率和医疗能力来综合考量。

5 疫苗有效性

在有关机构研究新冠疫苗时，本节考虑计算疫苗有效性方案，来避免药物在试验时出现药物有效而试验否定、药物完全无效而试验通过这两种情况。

疫苗进行临床试验前，相关部门会设定一个通过率。如果治愈率超过这个通过率，则判定疫苗为有效；如果最终治愈率不超过这个通过率，则判定疫苗无效。但是，在判定药物是否有效时，存在非药物作用治愈率，即疾病的自然痊愈率和药物的安慰剂作用。该试验目的在于减小非药物作用治愈率对判断药物本身治疗能力的影响。但是此类试验有可能出现药物有效而试验否定，或者药物完全无效而试验通过这两种情况。本方案将测算两种导致试验失败的情况出现的可能性。

设自然痊愈率p1，疫苗通过率p2（p1＜p2）。记试验总人数为n。有效治愈人数为X。

（1）当疫苗有效时

（2）当疫苗完全无效时

另一方面，如果有k∈N 个实验者被治愈（k≥np2），则会判定药物有效的概率为

同理，如果有m∈N 个实验者被治愈（m≤np1），则判定药物无效的概率为

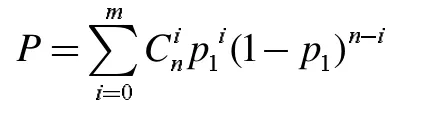
6 结论

本文首先设计了出行记录敏感问题调查设计方案，来调查测算谎报出行记录的人数比例。通过全概率公式计算出来估计结果，并通过分析比较调整了方案中的不同选项占比。由于结果表示在未诊断患病者中仍存在一部分潜在感染者，所以全民检测是有必要的。其次，因为在全民检测时的医疗设备的数量和效率有限等因素，设计了提高群体检测效率方案，即通过混合样本检测来加快检测效率。再次，利用统计概率，计算比较了不同方案的平均检测效率，并得到了在不同患病率的情况的最优检测方案。尽管检测效率可以提升，医院仍然存在一定的误诊率，于是设计了降低医院误诊率方案，即二次检测已确诊患病的患者，并通过全概率公式和贝叶斯公式来分别测算了一次检测和二次检测的误诊率。最后，由于对于本身患病却诊断不患病的误诊率难以降低，在未被隔离人群中不可避免的会存在患病者，为了控制疫情的传播，疫苗的研发非常重要，最后设计了计算疫苗有效性方案，并测算了两种导致试验失败的情况出现的可能性。希望以上四种模型可以帮助提高地方疫情防范工作的效率，以降低病毒传播率。