时间尺度上二阶Lagrange系统Noether对称性与守恒量
2021-01-21赵淑琼朱建青
赵淑琼,朱建青
(苏州科技大学数理学院,江苏 苏州 215009)
1988年,Hilger首次将离散和连续系统进行了统一,提出了时间尺度理论[1].对动力学方程进行时间尺度上的分析,可将方程内离散系统的差分方程和连续系统的微分方程相结合,从而更准确地描述了许多复杂动力学系统的物理本质.近年来,时间尺度已广泛应用于量子系统、动力学系统以及自然科学系统等[2-5].对于连续的和离散的时间变量,时间尺度理论可以建立更符合实际应用的数学模型来予以解决相应的动力学问题.例如将不同季节中昆虫繁殖行为看作动力学特征所提出的虫口模型[6]、关于拥有较长生产周期的商品产量和价格波动性进行动态均衡分析所提出的蜘蛛网模型[7]以及电路中电流改变率[8]等.
1918年,Noether基于Hamilton作用量在无限小变换下不变性的原理得到了Noether对称性与守恒量[9],Noether定理揭示了对称性和物理学守恒律之间的联系,即通过Noether对称性可以找到守恒量.随后,Karch和Desloge基于无限小变换下不变性首次提出了经典意义下Lagrange系统Noether定理[10].2004年,Bartosiewicz和Torres根据时间重参法将其推广到时间尺度上Lagrange系统的Noether对称性及其守恒量[11],并将离散系统与连续系统对称理论相统一.近年来,有关学者陆续给出了时间尺度上不同系统中相应的对称性与守恒量[12-18].
1848年-1858年间,Ostrogradsky和Jacobi开创了广义经典力学理论,广义经典力学系统是动力学系统中含有广义坐标对时间作高阶导数运算的Lagrange函数所构成的系统.自提出以来,它在力学、物理和数学方面应用广泛.关于广义经典力学Noether对称性的研究,已经有了许多进展,1973年,Anderson得到了广义经典力学中完整保守系统的Noether守恒律[19].乔永芬等人将结论推广到广义经典力学中完整非保守系统中[20-21].张毅等人基于正则作用量在r参数无限小下的广义准对称性研究了广义经典力学的Noether定理及其逆定理[22].另外Torres等人对时间尺度上的变分问题以及高阶变分问题进行了一定研究[23-26],为本文所用到的运算奠定了重要基础.但目前关于时间尺度上高阶Lagrange函数的动力学系统对称性与守恒量研究甚少,是一个较为新颖的课题,本文根据时间尺度上Hamilton作用量的不变性原理得到了时间尺度上二阶Lagrange系统Noether定理,并根据算例说明其应用.
1 时间尺度上二阶Lagrange系统的运动微分方程
设力学系统的位形由n个广义坐标qs(s=1,2,…,n)来表示,那么该系统Lagrange量
(1)
式中,I[qs(·)]为时间尺度上Hamilton作用量,其中
qsσ2(t)=(qs∘σ∘σ)(t),
式中,qsΔ2(t)为二阶delta导数,t∈T,L:R×Rn×Rn×Rn→R对其中各个元素都是C1的.
(2)
(3)
将(3)式代入(2)式可得,
(4)
即可得证.
根据文献[24],给出了时间尺度上高阶Lagrange系统运动方程
qsσr-1Δ(t),…,qsσΔr-1(t),qsΔr(t))=0,
(5)
其中,
根据上式可得时间尺度上二阶Lagrange系统的运动方程
(6)
2 时间尺度上二阶Lagrange系统Noether对称性及判据
对于时间尺度上二阶Lagrange系统,系统的Noether对称性是Hamilton作用量在无限小变换下的不变性.
由文献[13]可知,时间尺度上变分公式为
(7)
(8)
(9)
其中,α,α+dα为时间尺度T上定义的有界闭合线路.
另外由文献[27]可知,
(10)
对(8)式两边在时间尺度上求delta导数可得,
(11)
根据上式可得
δqsΔ2=qsΔ2(t,α+dα)-qsΔ2(t,α)=

(12)
通过(11)、(12)式可以得到
(13)
也可进一步推导得到
(14)
接下来考虑时间和坐标均变化的无限小变换群
(15)
在变换(15)下,时间尺度上二阶Lagrange系统Hamilton作用量(1)式可表示为
qs*(σΔ)*(t*),qs*(Δ2)*(t*))Δt*.
(16)

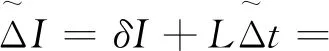
(17)

(18)
其中,
(19)
(20)
将(19)、(20)式代入时间尺度上二阶Lagrange系统的作用量即可得到(18)式.
在无限小变换(15)式下变分关系式可表示为
(21)
(22)
(23)
(24)

因此,由(17)式得到

(25)
对于无限小变换(15)式,若时间尺度上作用量(18)式在其上保持不变,那么

(26)
定义1在无限小变换(15)式作用下,如果作用量(1)式在该变换上有

(27)
成立,称变换(15)式为Noether意义下的广义对称变换.
根据广义对称变换定义,由(25)式可得
(28)
判据1在时间尺度上二阶Lagrange系统中,如果在无限小变换(15)式下有(28)式成立,则称变换为Noether意义下的广义对称变换.
定义2在无限小变换(15)作用下,如果作用量(1)式在该变换上成立
(29)

根据广义准对称变换,由(25)式可知
(30)

由t0,t1任意性可知,
(31)
判据2在时间尺度上二阶Lagrange系统中,如果在无限小变换(15)式下有(31)式成立,则称变换为Noether意义下的广义准对称变换.
3 时间尺度上二阶Lagrange系统Noether定理
在广义对称变换下,根据(26)式可得
(32)
将(6)式代入上式可得
(33)
对(33)式左右两边进行积分得到Noether守恒量
(34)
在广义准对称变换下,得到如下Noether守恒量
(35)
从而得到如下定理.
定理1如果无限小变换的生成元ξ0,ξs满足Noether等式(28),则时间尺度二阶Lagrange系统有Noether守恒量式(34).
定理2如果无限小变换的生成元ξ0,ξs和规范函数GN满足Noether等式(31),则时间尺度二阶Lagrange系统有Noether守恒量式(35).
推论1当T=R时,即σ(t)=0,μ(t)=0.由(34)式可以得到经典意义下二阶Lagrange系统下的Noether守恒量[20].
(36)
4 算例
设时间尺度
T={2n:n∈Z}∪{0},
(37)
系统的Lagrange函数为
(38)
下面研究该系统的对称性与守恒量.
首先,计算本题给出时间尺度的前跳算子以及步差函数
σ(t)=inf{2m:m∈[l+1,∞)}=2l+1=2t,
(39)
μ(t)=σ(t)-t=t.
(40)
其次,求生成元ξ0,ξs以及规范函数GN.Noether等式(31)给出
(41)
方程(41)有如下解
ξ0=1,ξs=t,GN=0.
(42)
最后,(42)式代入(35)式即得守恒量,
(43)
(43)式即为该系统对应的Noether对称性所导致的守恒量.
5 结论
本文研究时间尺度上二阶Lagrange力学系统的对称性,可有效地将连续系统与离散系统相统一.文章研究了时间尺度上二阶Lagrange系统Noether对称性问题.主要工作有:在时间尺度上根据二阶Lagrange系统的运动方程,给出了时间尺度上二阶Lagrange系统所对应的对称性定义及判据进而得到相应的Noether守恒量;最后当时间尺度取T=R时,即有
σ(t)=0,μ(t)=0,
则该守恒量可以退化到经典二阶Lagrange系统中Noether守恒量,并通过例子说明结果的有效性.而时间尺度是具有任意性的特征,因此本文的思想方法和结果更具有普遍性,可进一步拓展到时间尺度上高阶Lagrange系统Noether定理以及时间尺度上二阶Lagrange系统Lie对称性和Mei对称性等.
