低速冲击下纤维增强复合筋混凝土梁的动态响应

马志宏，马 钢，王志华

(太原理工大学 a.机械与运载学院，b.土木工程学院，太原 030024)

纤维增强复合筋(fiber reinforced polymer bar)因其密度小、质量轻、耐腐蚀以及良好的比强度和耐疲劳等特点，近年来被广泛应用到混凝土桥梁结构、防腐建筑和地下工程。国内学者从受弯承载力、挠度和裂缝的发展等方面对FRP筋混凝土构件的静态力学性能进行了大量的研究。董志强等[1]、郑乔文[2]、刘华杰[3]从试验、设计和性能预测方法等方面整理了FRP筋增强混凝土结构耐久性的研究进展，对FRP筋混凝土结构设计水平的提高、促进FRP筋的工程应用具有重要的借鉴意义。FRP筋混凝土结构除了受到静态荷载之外，还经常受到较大短时动态冲击荷载作用，而构件在冲击荷载作用下的动态力学响应往往不同于静态下的力学行为。李维博[4]、代小青[5]对冲击荷载下FRP与混凝土界面粘结力学性能进行了系统的研究，比较了动载与静载下界面特性的不同并对承受冲击荷载的FRP筋混凝结构的设计方法提出建议。赵灵雨[6]通过 CFRP 加固无腹筋混凝土梁在冲击荷载作用下的试验，研究了使用不同加固方式的混凝土梁的破坏力学性能。

上述成果主要集中在对FRP筋混凝土构件的动态粘结力学性能和FRP加固混凝土构件的动态性能试验的研究，但对于FRP筋单独作为受拉构件混凝土梁的动态响应的研究较少。本文对FRP筋梁在落锤冲击下响应特性展开研究，试验探讨了无腹筋FRP筋梁的破坏过程和破坏模式，通过对试验所得FRP筋混凝土梁的冲击力、跨中位移和支反力等数据分析，探讨了冲击过程中能量的转换与耗散情况，弥补了FRP筋梁构件在低速冲击下动态响应的研究空白，对于FRP筋混凝土梁在冲击荷载下的破坏分析及设计具有参考意义。

1 试验概况

1.1 材料特性

混凝土的强度设计等级为C40，水灰比为0.55.混凝土胶凝材料采用P·O 42.5的普通硅酸盐水泥，细骨料采用级配良好的天然中粗河砂，粗骨料采用粒径为5 mm的碎石。根据“混凝土结构试验方法标准”，制作三组尺寸为150 mm×150 mm×150 mm的标准立方块，在标准条件下养护28 d后测得混凝土的抗压强度为53 MPa.采用两种不同的FRP筋：CFRP筋(碳纤维增强复合筋)和BFRP筋(玄武岩纤维增强复合筋)。为使FRP筋与混凝土更好地粘结，采用了表面单缠绕FRP筋，如图1所示。由于FRP筋的应力应变基本上为线性关系，不存在与钢筋相似的屈服点和屈服平台，梁利利，樊成等[7-8]提出可取0.75倍的极限抗拉强度作为FRP筋的名义屈服点。本试验采用的碳纤维筋的极限抗拉强度为2 000 MPa，名义屈服强度为1 500 MPa，延伸率1.5%，弹性模量为160 GPa；玄武岩筋的极限抗拉强度为1 100 MPa，名义屈服强度为825 MPa，延伸率2.6%，弹性模量为55 GPa.

图1 FRP筋示意图Fig.1 Schematic diagram of FRP bars

1.2 试验梁参数及对比组

本试验采用无腹筋梁试件，无腹筋简支梁作为最简单的结构构件，一直是进行其他复杂构件研究的基础，与有腹筋梁相比，由于没有箍筋的作用，无腹筋简支梁的受力机理被大大简化，从而可以更直观地反映不同工况下纵向FRP筋的作用机理。FRP筋梁混凝土试件的尺寸如图2所示。FRP筋混凝土梁有三个变量：纵筋配筋率(0.6%，1.2%，1.8%)、冲击速度(2 m/s，3 m/s，4 m/s)和剪跨比(2.65，2，1.5)，以纵筋配筋率0.6%，冲击速度3 m/s，剪跨比2.65的构件作为对照组，分别改变纵筋配筋率、冲击速度、剪跨比，作为单变量实验组。表1为试件的试验参数。表1中C代表着碳纤维(Carbon fiber)，B代表玄武岩纤维(Basalt fiber)，ρ代表配筋率(Reinforcement ratio)，λ代表剪跨比(Shear-span ratio)，v代表速度(Velocity)。

图2 FRP筋混凝土梁尺寸Fig.2 Diagram of concrete beams with Fiber Reinforced Polymer Bars

1.3 试验装置及测量装置

试验设备如图3所示，采用Instron-9350落锤冲击试验机进行试验。锤头采用直径为25 mm的半球形锤头，采用附加钢板增加负重，整体质量为20.5 kg.锤头内部安装有力传感器，测量冲击力。通过升降落锤高度来改变冲击速度。在梁两支座处安放力传感器测量冲击过程中的支反力。在试验中传感器信号采样率统一为10 kHz；采用帧速率为10 000帧高速摄像机记录试验梁完整的冲击过程，并使用DIC进行数据处理，计算试验梁的位移；FRP筋跨中贴有应变片，采用多通道动态应变采集仪记录冲击过程中沿FRP筋轴向方向的应变。FRP筋混凝土梁加载装置见图4.

表1 试件设计分组Table 1 Specimen groups

图3 试验设备Fig.3 Test equipment

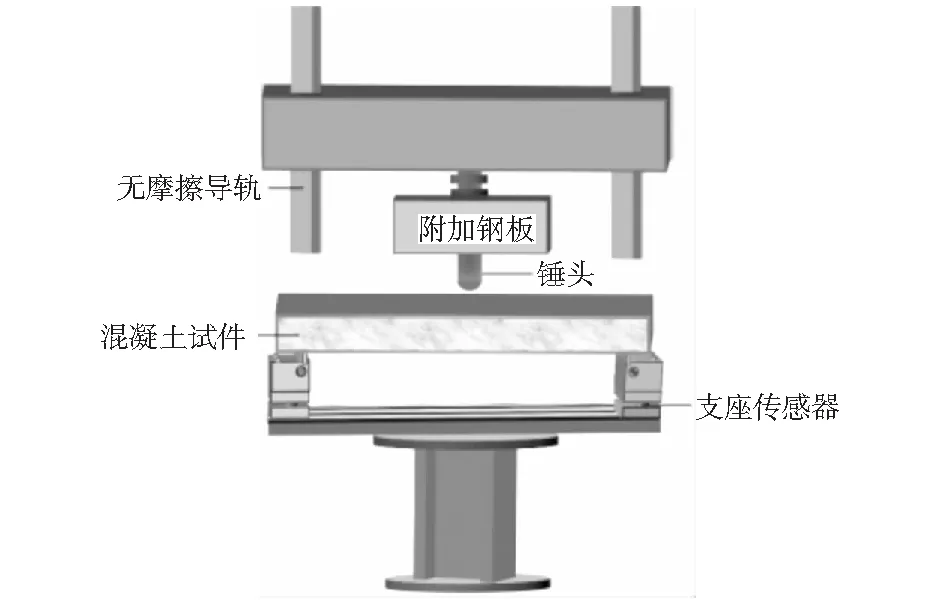
图4 FRP筋混凝土梁加载装置图Fig.4 Loading equipment of FRP reinforced beams

2 冲击试验结果

2.1 破坏形态

2.1.1不同纵向配筋下FRP筋混凝土梁的破坏形态

由图5可知， 两种FRP筋混凝土随着配筋率的增大裂缝宽度逐渐减小，且都呈现出竖向贯穿裂缝，这是由于FRP筋的弹性模量较低约为钢筋的60%.薛伟辰等[9-10]提出由于FRP筋的弹性模量低，FRP筋混凝土梁的挠度要比相应的钢筋混凝土梁大3倍左右。挠度增加较快，导致裂缝发展较快，甚至穿过受压区，使梁体被贯穿而破坏，同时很大程度上受到粘结性能的影响。由于FRP筋是各向异性材料，其纵向强度主要由纵向纤维的强度所决定。当FRP筋受拉时，其纵向应力在泊松效应的作用下变小，纵向应力降低，从而影响极限粘结强度的大小；当FRP筋受拉时，泊松效应会使得FRP筋在横截面上产生收缩，从而减低FRP筋与周围混凝土的机械咬合力和摩擦力并对粘结强度产生影响，这些原因造成裂缝扩展，进而导致裂缝高度迅速增加。

图5 不同纵向配筋率下FRP筋梁的破坏形态Fig.5 Failure modes of FRP beams with different longitudinal reinforcement ratios

2.1.2不同剪跨比下FRP筋混凝土梁的破坏形态

由图6可知，两种FRP筋混凝土梁在三组不同剪跨比下的破坏模态相似，随着剪跨比的减小，裂纹的形态由垂直裂缝向斜裂缝转变。同时由图7可知，试件CS-1剪跨比最大，对应的残余挠度最大2.62 mm；CS-3剪跨比最小，残余挠度最小0.04 mm.随着试件剪跨比的减小，CFRP筋梁构件的残余挠度也随之减小。BS-1剪跨比最大，对应的残余挠度最大5.1 mm，BS-3剪跨比最小，残余挠度0.05 mm，随剪跨比的变化，BERP筋梁与CFRP筋梁构件的残余挠度变化趋势基本一致。但通过比较两种不同筋的残余挠度可知，BS-1的残余挠度是CS-1的残余挠度的1.9倍，BS-3的残余挠度是CS-3的残余挠度的1.25倍，说明在相同剪跨比下，CFRP筋混凝土梁的残余挠度低于BFRP筋的残余挠度，且随着剪跨的减小，两者残余挠度之间的差距越来越小。

图6 不同剪跨比下FRP筋梁的破坏形态Fig.6 Failure modes of FRP beams with different shear span ratios

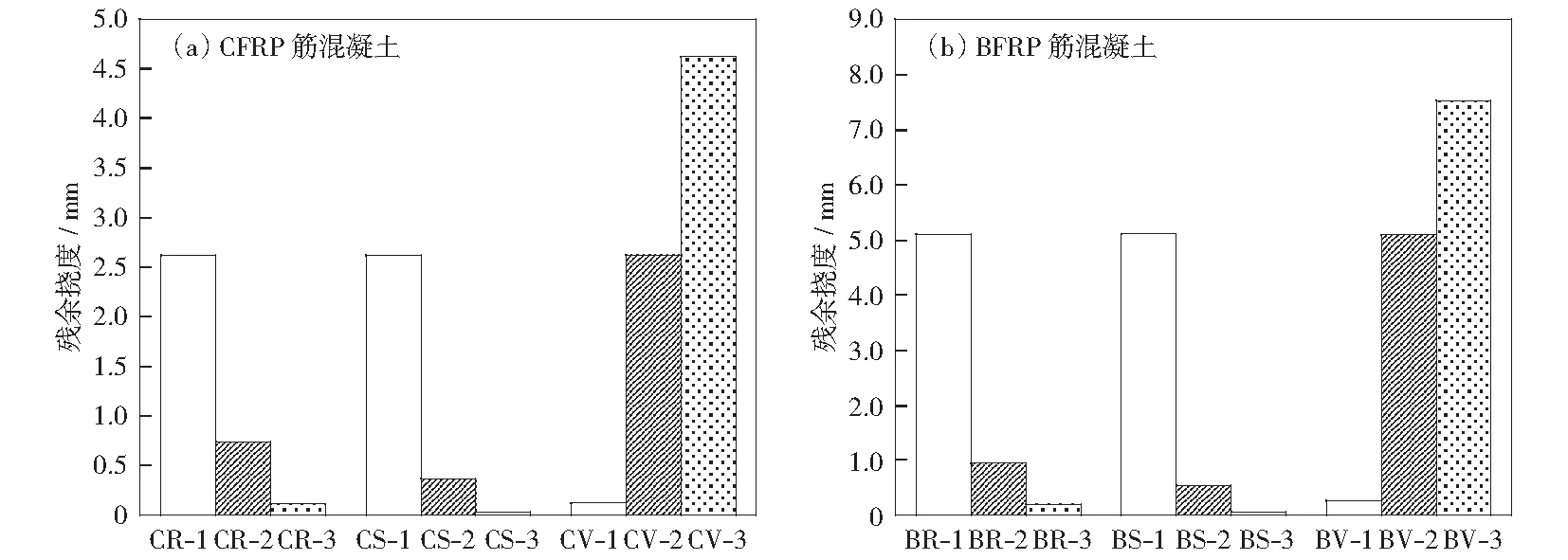
图7 不同工况下FRP筋混凝土梁的残余挠度Fig.7 Residual deflection of FRP reinforced beams under different working conditions

2.1.3不同冲击速度下FRP筋混凝土梁的破坏形态

图8(a)和8(b)为两种不同FRP筋混凝土梁在不同冲击速度下试件的破坏形态。冲击速度较小的试件与较大试件的破坏模式相比，跨中的斜裂缝分布数量要多，裂缝的扩展程度小于速度较大的试件。采用DJCK-2型裂缝宽度测试仪测量FRP筋梁的裂缝宽度，裂缝宽度柱状图如图9所示。试件CV-1速度最小，对应的裂缝宽度为0.15 mm；CV-3速度最大，裂缝宽度最大为0.72 mm.随着试件冲击速度的增大，CFRP筋梁构件的裂缝宽度也随之增大。BV-1速度最小，对应的裂缝裂缝宽度为0.22 mm，BV-3速度最大，裂缝宽度最大为1.2 mm.随冲击速度的变化，BFRP筋梁与CFRP筋梁构件的裂缝宽度变化趋势基本一致。但通过比较两种不同筋的裂缝宽度可知，BV-1的裂缝宽度是CV-1的裂缝宽度的1.5倍，BV-3的裂缝宽度是CV-3的裂缝宽度的1.6倍，表明在相同冲击速度下，BFRP筋混凝土梁的裂缝宽度是CFRP筋的裂缝宽度的1.5倍左右。

图8 不同冲击速度下FRP筋梁的破坏形态Fig.8 Failure modes of FRP reinforced beams under different impact speeds

图9 不同工况下FRP筋混凝土梁的裂缝宽度Fig.9 Crack width of FRP reinforced beams under different impact speeds

2.2 冲击力时程曲线和跨中位移时程曲线分析

由图10(a)和图10(b)中可知，刚开始梁受到落锤冲击，跨中位移迅速增加，出现冲击力峰值。当混凝土超过极限抗拉应变时，混凝土开裂，承载力迅速下降，中和轴逐渐上移，FRP筋承受大部分的拉力，跨中位移进一步增加达到峰值。随后FRP筋变形恢复，构件跨中位移减小。随着配筋率的增大，FRP筋混凝土冲击力峰值增幅较小，但跨中位移随配筋率的增大而明显减小。这是由于随着纵向配筋率的增加，FRP筋与混凝土的有效粘结面积越来越大，有效抑制了裂纹的发展，延缓了混凝土退出工作的时间。

由图11(a)和11(b)可知，CS-1的冲击力峰值为36.5 kN，CS-2和CS-3冲击力峰值分别为40.69，51.83 kN，相比CS-1分别提高了11.5%和42.8%；BS-1的冲击力峰值为29.1 kN，而BS-2和BS-3相比BS-1分别提高了7.3%和34.1%.通过比较两种不同筋的冲击力时程曲线和跨中位移时程曲线可知，剪跨比最大的CS-1冲击力峰值要比BS-1的冲击力峰值高25.4%，位移峰值比BS-1的位移峰值低23.5%， 剪跨比最小的CS-3的冲击力峰值要比BS-3的冲击力峰值高32.2%，位移峰值比BS-3的位移峰值低15%，说明在相同剪跨比下，CFRP筋混凝土梁与BFRP筋混凝土梁相比有更高的抗冲击力和较小的变形，且结合上述残余挠度和裂缝开展柱形图可知，CFRP筋混凝土梁的残余挠度和裂缝开展宽度均小于BFRP筋混凝土梁。综上所述，说明在相同剪跨比下CFRP筋的抗冲击性能优于BFRP筋。

由图12(a)和图12(b)可知，CV-1的冲击力峰值为28.9 kN，CV-2和CV-3冲击力峰值分别为36.5，49.83 kN，相比CV-1分别提高了28.9%和72.4%.冲击力峰值和跨中位移随着冲击速度的增大而明显增大，而冲击力作用时间随之减小。同时对比CV-3和BV-3的冲击力时程曲线和跨中位移时程曲线可知，BFRP筋混凝土梁与CFRP筋混凝土梁两时程曲线形态基本一致，在相同冲击速度下，CV-3的冲击力峰值要比BV-3的冲击力峰值高15.5%，位移峰值比BV-3的位移峰值低13.2%，说明CFRP筋梁的抗冲击性能优于BFRP筋梁的抗冲击性能。

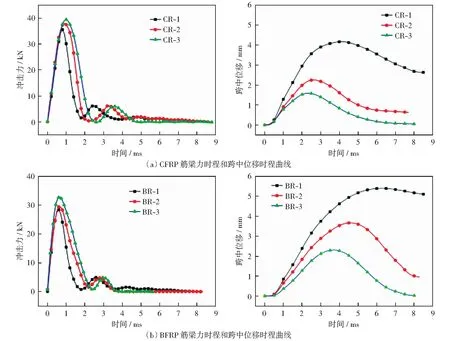
图10 不同纵向配筋率下FRP筋梁的力时程和跨中位移时程曲线Fig.10 Time history of impact and displacement for FRP beams with different longitudinal reinforcement ratios

图11 不同剪跨比下FRP筋梁的力时程和跨中位移时程曲线Fig.11 Time history of impact and displacement for FRP beams with different shear span ratios

图12 不同速度下FRP筋梁的力时程和跨中位移时程曲线Fig.12 Time history of impact and displacement for FRP beams under different impact speeds

3 冲击试验分析及讨论

3.1 破坏过程分析

由图13分析可知，梁构件的破坏过程可分为四个阶段。

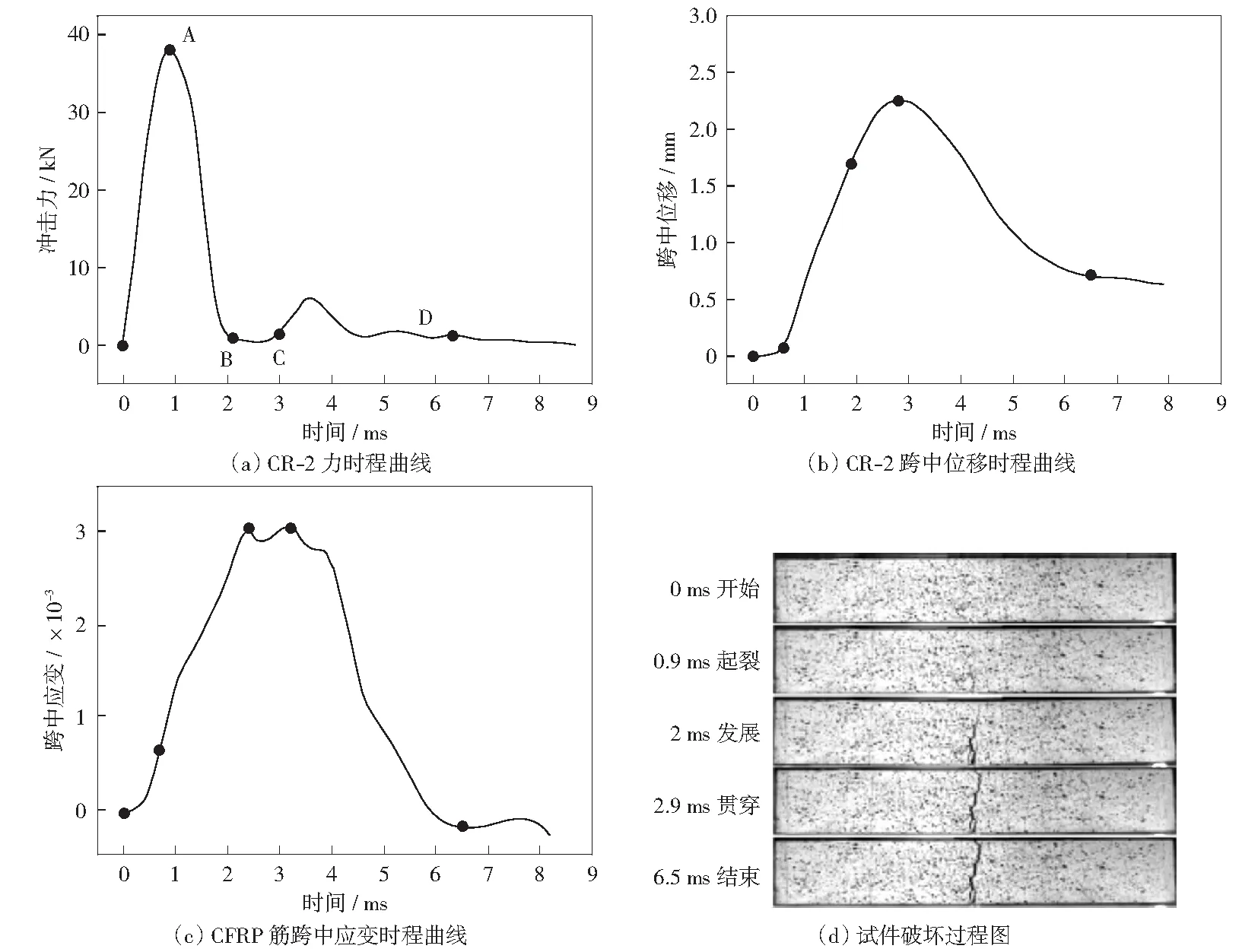
图13 破坏过程分析Fig.13 Failure process analysis

1) 冲击响应阶段(OA段(0～0.9 ms))：冲击力稳定上升，跨中位移几乎保持不变，此时FRP筋应变较小，FRP筋与混凝土保持良好的整体性，梁整体受压没有裂纹产生。

2) 损伤起裂阶段(AB段(0.9～2 ms))：混凝土出现裂缝，梁的刚度开始弱化，冲击力开始急剧下降，跨中位移迅速增加，主裂缝处FRP筋开始参与变形。

3) 裂缝发展阶段(BC段(2～2.9 ms))：在此阶段混凝土裂纹延伸或贯穿，FRP筋承受大部分拉力，但未达到名义屈服点，此阶段为FRP筋的主要受力阶段，跨中位移进一步增加，达到位移峰值。

4) 回弹阶段(CD段(2.9～6.5 ms))：在这一阶段，FRP筋应变开始减小，由于FRP筋与混凝土之间的粘结力，FRP筋使梁的变形恢复，梁的跨中位移减小。

3.2 惯性力的计算

在冲击荷载作用下，为了正确研究FRP筋混凝梁的结构安全性，对构件承载力进行估计是十分重要的。BENTUR et al[11]通过研究混凝土梁在冲击载荷下的力学行为，发现在落锤冲击试验中锤头力传感器测得锤头冲击力pt包含了两部分力：使混凝土构件变形的荷载pd和使梁构件产生加速度的惯性力pi.三者的关系为：

pt(t)=pd(t)+pi(t) .

(1)

式中：pd为等效变形荷载，N；pi为等效惯性力，N；t为时间，s.

向达等[12]发现惯性力主要是由于混凝土的损伤导致波通过混凝土时速度发生变化而在轴向产生加速度。许斌等[13-14]对混凝土梁构件进行了落锤冲击试验，结果显示当冲击力达到最大值时没有明显的竖向位移发生，试件没有整体耗能，冲击力基本用于梁的加速，因而要真实反映梁的抗冲击承载力就需要消除惯性力的影响。本文基于BENTUR et al[11]提出的惯性力计算方法对FRP筋混凝土梁的惯性力进行了计算。计算遵循以下基本假设：1) 截面应变保持平面；2) 未考虑混凝土的抗拉强度；3) 忽略剪力的影响；4) 未考虑混凝土与FRP筋粘结滑移的影响；5) 在冲击作用下FRP筋混凝土梁位移分布形式为正弦分布。

图14为广义惯性力的计算示意图，由此得出沿梁长度方向的位移表达式如下。

支座之间梁的位移：

(2)

支座之外梁的位移：

(3)

式中：u0(t)为梁跨中位移，m；x为距离左侧支座的距离(支座之间)，m；y为距离右侧支座的距离(支座之外)，m；l为梁跨度，m.

在计算梁上分布的惯性荷载pi时可根据虚功原理由作用在梁跨中的广义集中荷载等效替代，等效过程如下式所示:

(4)

(5)

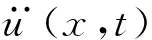
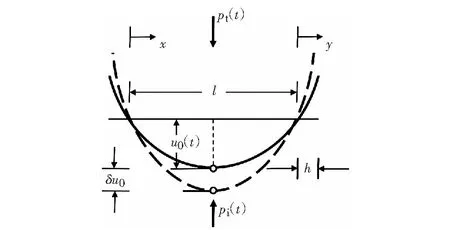
图14 广义惯性力的计算示意图Fig.14 Definition of terms for calculation of generalized inertial load

由图15(a)可知，冲击力向下为正，惯性力和支座反力向上为正。冲击力的第一个主波峰峰值略高于惯性力，此时支反力几乎为零，说明了第一个波形的冲击荷载主要使梁加速。随后支反力开始增加与除去第一个波峰的冲击力分布相似。

根据达朗贝尔原理，惯性力与支座反力之和等于冲击力。图15(b)将试件CR-2的惯性力、支反力两者之和的时程曲线与冲击力时程曲线进行了比较。结果表明，两曲线在趋势上一致且冲击力最大误差小于10%，验证了RC梁惯性力计算公式用于FRP筋混凝土梁依然能够保证其精度。

3.3 能量分析

为了分析梁能量的转换和耗散过程，可以将输入的总能量Wt分为两部分：引起梁运动的动能Wk和用于试件损伤与破坏过程中所吸收的能量Wf.通过将力-时程曲线与位移-时程曲线转化为力-位移曲线，并对力-位移曲线进行积分，计算出各部分能量。计算公式如下所示：

(6)

(7)

(8)

图15 冲击力、惯性力和支反力时程曲线Fig.15 Time history diagrams of impact force, inertia force, and reaction force

由图16分析可知，在0.9 ms之前的阶段，由于受到落锤冲击，CFRP筋混凝土梁动能快速增加。在0.9 ms以后，FRP筋混凝土梁试件开始出现裂缝，随着裂缝的发展和FRP筋的变形，耗能越来越大。此外，FRP筋的树脂强度低于混凝土的抗压强度和FRP筋中纤维的抗拉强度，在冲击过程中，梁试件中FRP筋发生了滑移，使得筋表面的树脂发生变形或横肋破坏。树脂作为FRP筋的一部分，在此过程中也消耗了一部分能量。最终输入的总能量全部转化为用于试件损伤与破坏过程中所吸收的能量。

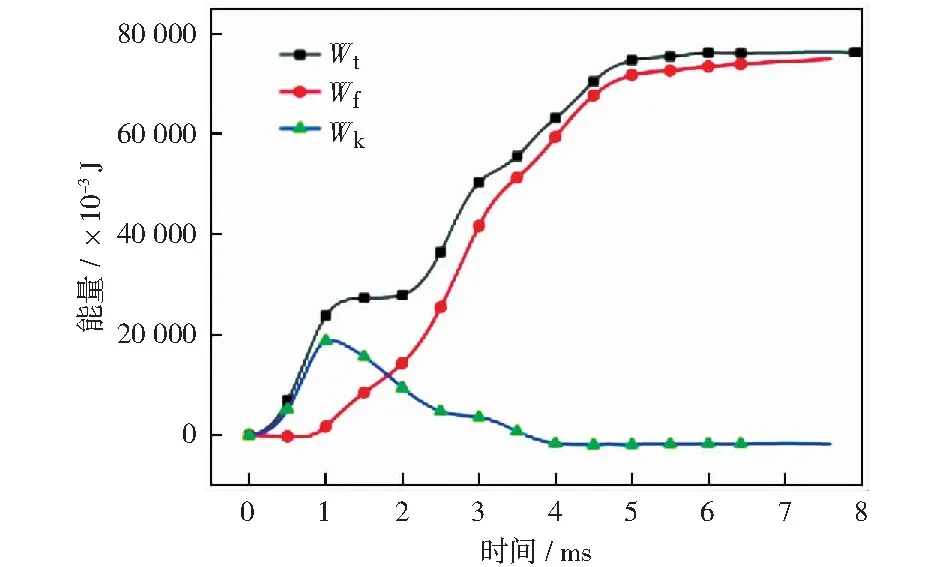
图16 能量变化时程曲线Fig.16 Energy-time history curves

4 结论

本文以FRP筋混凝土梁为研究对象，通过对冲击载荷下试件的破坏特点、受力机理以及能量吸收等方面的分析，得出了以下主要结论。

1) 利用落锤冲击试验机对不同种类FRP筋混凝土梁试件进行了试验，试验结果显示：两种FRP筋混凝土在三种不同工况下的破坏模态相似。随着配筋率的增大裂缝宽度逐渐减小，且都呈现出竖向贯穿裂缝；随着剪跨比的减小，裂纹的形态由垂直裂缝向斜裂缝转变，CFRP筋混凝土梁和BFRP筋的残余挠度之间的差距由1.9倍减小到1.25倍；随速度的增大，试件裂缝的数量减小宽度增大。在相同冲击速度下，BFRP筋混凝土梁的裂缝宽度是CFRP筋的裂缝宽度的1.5倍左右。

2) 结合冲击力、位移以及CFRP筋应变响应曲线，研究了FRP筋混凝土梁的破坏过程。通过分析可知，梁构件的破坏过程可分为四个阶段，即冲击响应阶段：冲击力稳定上升，梁整体受压没有裂纹产生；损伤起裂阶段：混凝土出现裂缝，梁的刚度开始弱化；裂缝发展阶段：FRP筋的主要受力阶段，跨中竖向位移达到峰值；回弹阶段：FRP筋应变减小，梁的变形恢复。

3) 在假定FRP筋混凝土梁在落锤冲击下的位移分布形式为正弦分布的基础上，利用虚功原理得到了广义惯性力的计算公式。通过对冲击力时程曲线与惯性力、支反力两者之和的时程曲线的比较分析，验证了RC梁惯性力计算公式用于FRP筋混凝土梁的计算依然能够保证其精度。最后利用力-位移曲线分析了FRP筋混凝土梁在低速冲击下的能量耗散及转换。