改进的Q-Learning算法及其在路径规划中的应用
2021-01-21毛国君顾世民
毛国君,顾世民
(福建工程学院 机器学习与智能科学研究所,福州 350118)
人类知识的获取是通过感知环境(Environment)并与之交互来完成的,因此所谓的智能学习就是智能体(Agent)不断适应环境来完善自己的过程。强化学习(reinforcement learning,RL)是机器学习的方法论之一,用于描述和解决智能体在与环境的交互过程中如何学习和优化策略的问题[1]。事实上,许多应用中的环境是动态变化和不确定性的,如机器人的路径规划问题,智能体必须在不确定性环境中主动地对周围环境进行探索[2-3]。在探索过程中不断地认知环境,形成适应环境的正确行为。
强化学习不同于目前广泛研究的监督学习(supervised learning)和无监督学习(unsupervised learning),它的学习不是被动地从已有数据中进行归纳或提取,而是一个主动适应环境并进行自我完善的过程。强化学习是从计算机科学、数学、神经学等多个相关学科发展而来的,已经成为机器学习的主要分支之一[4-5]。由于强化学习强调在环境变化情况下智能体的主动学习,因此近年受到广泛关注,并在机器人控制以及智能计算等领域得到应用。
基本的强化学习思想是通过智能体对当前环境状态的感知,并对可能采取的动作(Action)获得的回报(Reward))进行评价来完成的。图1给出了强化学习的基本模型[6]。

图1 强化学习的基本模型Fig.1 Reinforcement learning model
强化学习是一个“探索-利用”的迭代过程[6-7]。首先,智能体通过感知环境的当前状态,并采取某一个动作来探索环境,探索的结果一般以某种形式的奖励或者回报来表示。然后,对已经获得的回报进行评价,寻找在当前状态下的一个最优的动作加以利用。当然,“探索-利用”是一个不断反复循环的过程,直到获得满意的最终策略。
不同的强化学习算法在“探索”“利用”方法及其融合机制上会有所差异。就强化学习的经典算法Q-Learning而言,在探索阶段所用的方法是ε-贪心(ε-greedy)方法,即优先利用最大Q值对应的动作来向前推进探索。
传统的Q-Learning存在探索效率低下的致命问题[8]。实际上,探索与利用是强化学习的两个不可分割的部分,同时也是一对矛盾共同体。当智能体过多地探索环境时必然会导致效率下降,但当智能体在探索不充分情况下盲目地相信某种决策而加以利用时也会增加后续的探索代价。因此,制定一个合适的探索计划来平衡探索和利用的代价,以便在正确决策的同时尽可能地提高收敛速度,是强化学习的一个重要任务。
本文针对传统的Q-Learning算法收敛速度慢的问题,提出一个改进算法ε-Q-Learning.基本思想是通过动态地改变搜索因子参数来快速适应环境的变化,既可以提高探索效率,也可以避免陷入无效的局部搜索,因而提高全局优化的可能性。
1 相关工作
路径规划(Path planning)是机器人研究领域的一个关键性的工作,同时也是许多应用(如电子游戏、无人驾驶等)的基础。1986年,Khatib第一次提出用人工势场法(Artificial potential field method)解决了机器人躲避障碍物的问题,此后这个方法也成为许多路径规划研究与应用的基础[9]。然而,随着人工智能技术的研究进展,利用智能学习方法来解决路径规划问题成为新的发展趋势,其中强化学习扮演了十分重要的角色。例如:利用BP神经网络和Q-Learning算法,在未知环境下的自主避障问题被研究[10];将模糊逻辑引入到强化学习中[11];Agent的自主强化学习等[12-14]。我国学者也在机器人、无人机等强化学习模型方面开展了卓有成效的工作[15-16]。
此外,强化学习的模型或者算法基本都是基于马尔可夫(Markov)属性构造的[4-5]。马尔可夫属性是指一个系统下的状态只与当前状态有关,而与更早之前的状态无关,即公式(1):
P(st+1|st,st-1…s1)=P(st+1|st) .
(1)
基本的马尔可夫决策(MDP)[4]模型由一个四元组
其中,S表示环境中的所有状态集合;A表示是作用于环境的所有可能动作集合;P表示状态之间的转移概率;R表示采取某一动作到达下一状态后的回报。
基于MDP模型,目前的强化学习算法主要是围绕着回报的评价机制、状态与动作的影响估算等方面进行研究和实践,因而出现了不同的解决模型,也在算法的可用性等方面进行有效探索[17-18]。
目前的典型强化学习算法大致有3种,分别为Q-Learning算法、Sarsa算法和TD算法[4,16-17]。分析这些典型算法的理论基础,基本上是由2个实体和4个评价机制组成的。当然在不同的强化学习算法中可能依赖的评价机制或者函数有所侧重。
实体主要有环境和智能体。
1) 环境是学习的对象。一般而言,在一个确定时刻,一个环境一定有一个确定的状态(State),但是当智能体在该环境中活动后,其状态就会发生改变。因此智能体必须对其活动结果(下一个状态)有一个估算,并借此形成下一步的决策。
2) 智能体则是学习者。一般而言,智能体是通过采取动作(Action)来适应环境的。就是说,智能体需要通过不断地尝试某状态下可能动作的效果,来认知环境并采取恰当的动作来继续探索。
评价机制包括4个基本方面。
1.1 策略π
在强化学习过程中,智能体在某个状态采取什么样的动作到下一个状态是由策略控制的。简单地说,策略就是从状态到动作的映射。特别地,当环境存在障碍或者陷阱时,策略就必须保证下个动作不能碰到障碍或者掉入陷阱。策略的好坏决定了智能体行动的好坏,进而决定了整个算法的学习质量。
1.2 回报R(s)
回报R(s)是智能体处在状态s下可能形成正确决策的可能性:可能性大则回报值就大,反之亦然。强化学习的任务就是不断地探索来改变状态,达到寻优目的。因此,一个状态s的回报是在不断地探索中加以完善的。
给定一个探索的时间序列<1,2,…,t,t+1,…>,设当前时间为t,根据马尔可夫属性,则R(s)的理论值就是:
Rt(s)←f(Rt(s),Rt+1(s),…) .
(2)
其中,Rt(s)为状态s在t时刻的回报,f则代表对向前探索的回报值的综合评价函数。
基于回报估计是强化学习的理论基础,也是构建强化学习算法的基本依据。当然,不同的算法在实现路径上会有不同,在回报值的计算及其评价函数的设计上会有所区别[19]。
从公式(2)可以看出,一个状态s的理论回报值的计算是一个反复探索直到稳定的过程。特别地,当环境的状态空间很大或者情况复杂的情况下,这种探索可能耗时很长、甚至是无限的。因此,实际的算法经常使用的是有限T步的探索策略。此外,在回报值的综合评价函数方面,最常用的方法是“折扣累计回报”,即给定探索的步数T>0和折扣因子γ∈[0,1],基于有限折扣累计回报策略,t时刻的状态回报值计算如下:
R(s)←Rt(s)+γ×Rt+1(s)+…+γT×Rt+T(s) .
(3)
1.3 状态值函数V(s)
如上所述,环境的变化在强化学习中表现为状态的更新。值函数将理论上的回报值转化成可以计算的V值、并通过反复迭代来实现强化学习的目标。基于V值学习的模型和算法已经成为强化学习的一个重要方法。
给定一个时间t和当前状态st,值函数方法是一个“前探+回推”的过程。基于有限折扣累计回报策略,下面的公式(4)给出了对应值函数的计算方法:
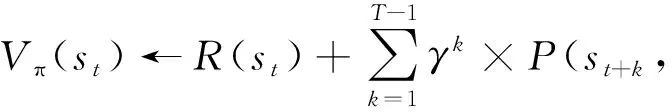
(4)
其中:π是学习的策略;R(st)是t时刻的回报(也被称为t时刻的即时回报);P(s1,s2)为状态s1可能转移到状态s2的概率;γ∈[0,1]是折扣因子,而且整个后面一项是前探T步的V值函数的综合评估,即相对于即时回报R(st)而言,这部分是t后可能的回报(强化学习中也被称为未来回报),它需要通过V值的迭代计算来完成。
1.4 动作值函数Q(s,a)
在强化学习中,状态的转移是通过执行动作来完成的。一个状态下实施了某种动作就到达一个新状态。这在机器人系统或者棋牌对弈系统中得到充分体现。例如,在围棋对弈系统中,每落一个棋子就意味着棋局(状态)发生改变,但是这种改变需要持续进行评价。同样,在机器人路线规划中,机器人每前进一步意味着新的状态产生,但是这并不意味着接近目标点,所以每个动作引发的状态更新都需要进行评价并累计到之前的奖励回报中。
假设一个环境用状态集S和动作集A来描述。给定t时刻的当前状态s∈S,动作a∈A是s状态下可以执行的一个候选动作,则π策略下的关于状态s和动作集a的回报可以用动作值函数来估计。公式(5)给出了对应的表达公式:

(5)
其中:R(st)和γ分别是t时刻的立即回报和折扣因子;A(*)是状态*可能采取的下动作集合,整个的后面一项就是t时刻的未来Q值的累计估计。
除了经典的上述3种算法外,还有在此3种算法基础上大量改进的强化学习算法,比如在Q-Learning中加入多个智能体,将TD与神经网络相结合以及将启发函数与Sarsa相结合等等,这些算法都在实验中表现出了优异的成绩。
2 Q-Learning算法分析
2.1 基本原理
Q-Learning是强化学习三种最流行的算法之一,是基于Q值迭代的无模型算法。如前所述,给定某一时刻的状态si和准备采取的动作ai,Q(si,ai)就是在该时刻的状态si下采取动作ai获得回报的估计值。理论上讲,当探索了一个给定时刻的状态si和所有可能动作A(si)后,就可以根据环境的反馈回报信息选取一个最优动作进入下一次状态si+1;如此反复直到终点或者人为终止,一次迭代过程结束。当然,一个状态的Q值也是随着探索的不断推进在不断更新中,直到所有状态的Q值相对稳定为止。
Q-Learning算法的特点是根据潜在的状态与动作来构建一张二维表(被称为Q-table)来存储Q值,然后通过查表方式获得Q值来寻找最优的动作。该方法具有简单直接的特点,在环境大小适中的应用场景中(如简单棋牌对弈等),已经证明非常有效。
Q-table的数据结构简单易用,表1给出了一个4个状态、2个动作的结构示意。

表1 Q-Table结构示意Table 1 Q-Table schematic
基于Q-table,Q-Learning算法主要使用公式(6)来更新Q值:
Q(s,a)←Q(s,a)+α×((R(s′)+γ×maxa′∈A(s′)
{Q(s′,a′)-Q(s,a)}) .
(6)
其中:s和s′分别是当前状态和下个状态,a则是使s到s′的有效动作,而A(s′)则是下状态s′可能采取的候选动作;α∈[0,1]被称为为学习率,用于调节学习过程中的可能误差;γ为折扣因子。
依据公式(6),Q-Learning算法在一个特定状态下将贪婪地对所有可能的路径进行探索,每前进一步都是在寻找当前状态下的局部最优解。
为了准确刻画改进的算法,本文采用的主要符号及其意义见表2.

表2 符号表Table 2 Symbols in this paper
算法1给出了Q-Learning算法的伪码描述。

Input: learning rate α, discount factor γ, greedy factor ε, reward matrix R(|S|,|A|), maximum forward steps maxStep, maximum number of Q-table modifications maxIter.Output: Q-table Q(|S|,|A|).Process:Initialize Q-table;所有Q(s,a)元素为0iter←0;Reapeat //循环更新Q表 s←start; 开始状态为start step←0; Repeat// 循环找终点terminal: For(each action a∈A(s)) call ε-greedy obtain a'∈A(s);//用贪婪策略前探 Q(s,a)←Q(s,a)+α*(R(s)+γ*(Q(s(a),a')-Q(s,a))); s←s(a'); step++; Until (step>=maxStep) or (s=terminal) iter←iter++;Until (iter>=maxIter) or (Q-table no again change)Return Q-Table.
值得注意地是,考虑到现有Q-Learning算法的描述大多过于简单[4,8],不利于读者阅读和本文后面算法的介绍。算法1把整个Q-Learning的主要步骤整合到一起,对细节进行了更详细描述。
简单地讲,Q-Learning算法除了必要的初始化外,主要是一个双层循环:
1) 在内层循环里要完成一次从起点到终点状态的探索,并对探索过的路径的Q值进行更新。它的理想出口是每次探索都能到达终点。这种(内循环)正常出口只意味着找到一条可行的路径来完成从起点到终点的工作,但它不一定是最优的,因此还需要通过Q-Table的迭代来寻优。当然,当内循环人为终止(超过步骤阈值)时,就说明本次探索失败,需要重新开始探索。此外,在一个状态下寻找下动作采用的是ε-greedy策略。
2) 外循环的正常结束条件是Q-table不再变化。这意味着经过多次迭代后,已经产生了从起点到终点状态的稳定情况,因而达到了优化的目标,最后的答案也就是从起点到终点的“最大Q值”形成的路径。当然,当外循环触动“意外的结束条件”时,就说明循环探索已经达到极限,没有必要继续下去了。
2.2 改进Q-Learning算法
强化学习和监督学习、半监督学习等其他学习方法不同,它需要不断探索环境并获得反馈。目前最常用的探索策略有两个:贪婪策略和Boltzmann策略[4-5]。
一般地讲,Boltzmann基本上是随机选择策略,缺乏探索的目的性,效率很难保证,特别是在复杂情况下很难完成。相对来说,贪婪策略增加了探索的目的性,但是很容易陷入局部优化,甚至经常“碰壁”而被迫终止。目前的算法也都致力于解决该问题,但是仍然存在很大的改进空间。
本文引入动态搜索因子ε,尝试改进Q-Learning算法。算法2给出了改进Q-Learning算法ε-Q-Learning的伪码描述。

Input: learning rate α, discount factor γ, basic greedy factor ε, greed incremental θ, reward matrix R(|S|,|A|), maxi-mum forward steps maxStep, maximum number of Q-table modifications maxIter.Output: The optimal path P.Process:Initialize Q-table;所有Q(s,a)元素为0iter←0;Reapeat //循环更新Q表 s←start; 开始状态为start step←0; Repeat// 循环找终点terminal: For(each action a∈A(s)) IF rand()<ε Then a'← a random forward action from s Else call ε-greedy get a'∈A(s);//用贪婪策略前探 Q(s,a)←Q(s,a)+α*(R(s)+γ*(Q(s(a),a')-Q(s,a)) End Do s←s(a'); step++;Until (step>=maxStep) or (s=terminal)iter←iter++;If (step>=maxStep) Then □←□+θElse Then □←□-θ;Until (iter>=maxIter) or (Q-table no again change);For (s=start To terminal) Do a←argmax{Q(s,a)|a∈A(s)} P←P+;Return P.
ε-Q-Learning主要改变是根据环境的反馈来动态调整贪婪因子ε.正如算法2中间描述那样,ε-greedy策略是通过条件rand()<ε来决定是随机选择还是选择最大Q值的下动作。很显然,ε越大则随机搜索下动作的概率就会增大,这在一定程度上避免陷入局部优化。
算法2引入动态的贪婪因子ε.简单地说,在算法2中,假如在一次从起点到终点的探索失败,则通过增大ε来使下一次探索的随机性增大,以免陷入之前的局部优化困境。反之,则通过减少ε来增加目的性。当然,算法2中的基础贪婪因子ε和增幅θ是一个经验值,也需要根据应用中环境的不断变化进行尝试实验来确定。
3 实验结果及分析
实验在Anaconda上采用36×36的迷宫环境模拟智能体运动进行仿真,将改进的ε-Q-Learning算法和传统的Q-Learning算法进行比较性实验。实验中使用的主要参数见表3.

表3 实验参数设置表Table 3 Main parameter setting for the experiments
智能体所在位置的坐标(x,y)对应Q-table的一个状态,智能体的动作选择有4种:北、南、西、东,分别用N、S、W、E来表示,这样Q-table的容量就是1 296×4.迷宫中还有障碍物,若进行动作选择后碰到障碍物和迷宫墙壁则智能体保持在原状态,否则进入下一个状态。智能体的开始位置设置在迷宫环境的(0,35)处,目标位置设置在(35,0)处。
根据上述的实验环境和参数设置,使用上面的算法1和2,我们进行了损失函数、运行效率和收敛性等方面的跟踪实验。实验结果如图2-5所示。在图中圆点表示的是ε-Q-Learning算法的值,线表示的是传统的Q-Learning算法的值。
3.1 损失比较
算法的损失函数所反映的是算法所形成的路径与最优路径的相似度。强化学习中已经出现了7种损失函数:平方误差损失函数、绝对误差损失函数、Huber损失函数、二元交叉熵损失函数、Hinge损失函数、多分类交叉熵损失函数、KL散度损失函数。本文采用是绝对误差损失函数,公式(7)给出了它的计算方法:
L=|y-f(x)|/maxIter .
(7)
式中:y表示每次迭代的路径的总回报,f(x)表示表示人为设置最优路径的总回报。显然,损失函数的值越小越好。图2给出了两种算法在损失函数值上的变化趋势。
分析图2,ε-Q-Learning算法和Q-Learning算法在迭代次数n<60时对环境模型的学习都不足够深入,且ε-Q-Learning算法也没有很好体现出其调节ε效果。然而,但当n超过60以后,由于ε-Q-Learning算法对环境模型的学习越来越深入,ε也越来越优化,ε-Q-Learning算法就显示出了它明显的优越性,其损失函数值渐渐小于传统的Q-Learning算法,且更快收敛于稳定值。
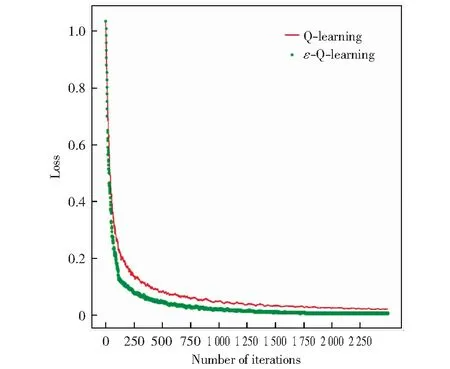
图2 算法损失函数图Fig.2 Loss function graph
3.2 运行效率比较
图3给出了两种算法的运行时间比较。
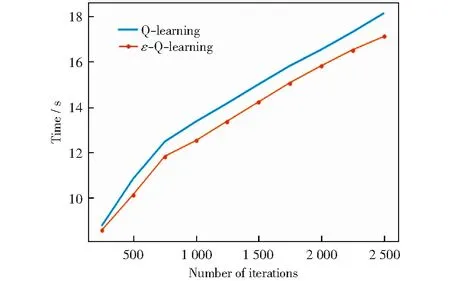
图3 算法时间图Fig.3 Executive time graph
从图3中可以看出,在250次迭代之前,ε-Q-Learning算法的运行时间和Q-Learning算法基本没有差距。然而,随着迭代次数的增多,ε-Q-Learning算法对环境越来越适应,学习效率提升,算法的运行效率更高。
3.3 回报函数值比较
迭代过程中总回报函数值的变化反映了算法的收敛情况。图4是两个算法的总回报的比较结果。
从图4中可以看出在n<60时,由于迭代次数太少,ε的调整效果并不明显,因此ε-Q-Learning算法中的回报值与Q-Learning算法大致相同。当n≥60时,由于ε-Q-Learning开始适应环境,当迭代500次后总的回报函数值基本不再变化。因此,从回报函数值的变化,可以推断出ε-Q-Learning算法要比Q-Learning算法的收敛性要好。

图4 算法总回报图Fig.4 Cumulative rewards graph
3.4 探索步数比较
总的探索步数反映学习算法寻优过程所付出的代价。一般而言,一个算法使用更少的步数而找到最优解,那么它的代价就小,因而性能也就要好。图5给出了两个算法随着迭代次数增加时累计的总步数的变化情况。
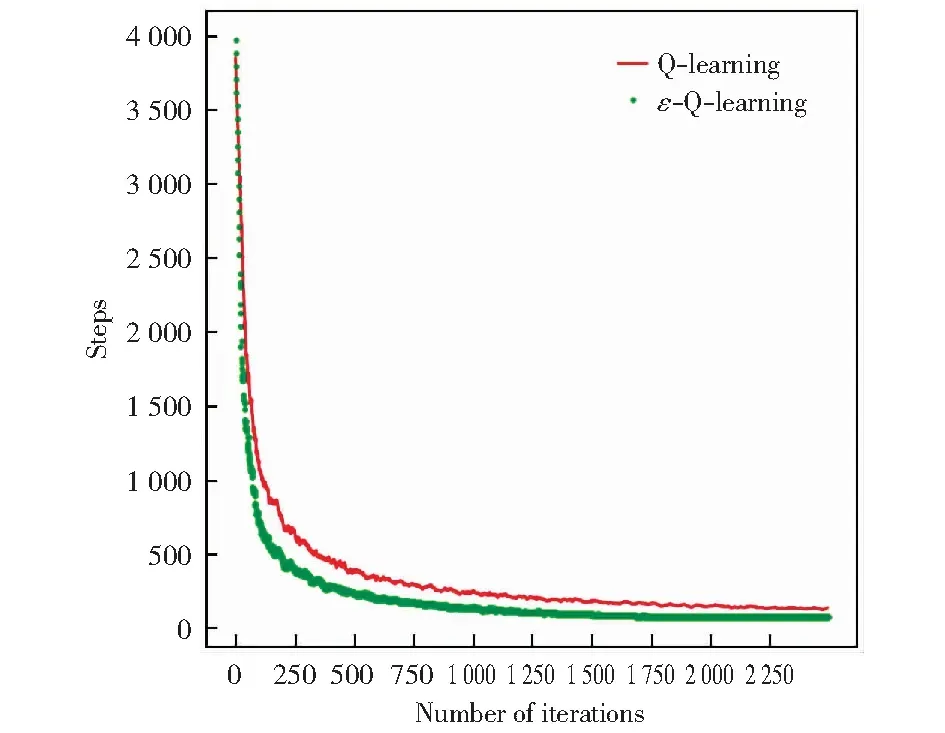
图5 算法步数图Fig.5 Cumulative step graph
从图5中可以看出,当n<5的时候,ε-Q-Learning算法的总步数是大于Q-Learning算法的,这很有可能是算法随机探索所造成的。当5≤n<60时,两种算法的总步数大致相当。但是,当n≥60时,ε-Q-Learning算法步数就逐渐开始小于Q-Learning算法的步数,而且随着迭代次数的增多,ε-Q-Learning算法的总步数基本稳定,收敛也比Q-Learning算法要好些。
4 总结
传统的Q-Learning算法在路径规划中存在收敛速度慢和易陷入局部优化等问题,本文提出了一种改进的ε-Q-Learning算法。通过引入动态的探索因子ε,不仅可以有效地提高算法的搜索效率,而且也能保证最终路径的优化。ε-Q-Learning算法根据每一次迭代的总步数来判断本次探索的有效性,并通过修改贪心算法的搜索因子ε来提高下次探索的成功率。特别是,动态的搜索因子技术可以有效地避免局部搜索困境,提高探索的成功率。实验结果表明,改进的ε-Q-Learning算法相比现有的Q-Learning算法,在收敛速度、运行效率和搜索代价等方面都表现出不同程度的优势。
