膨胀土一维湿化变形时效特性的半经验法研究

王金淑，吴光

(西南交通大学 地球科学与环境工程学院，四川 成都 611756)

0 引 言

膨胀土通常处于非饱和状态，其工程性状对含水率和吸力的变化均很敏感。膨胀土地基上的轻型结构物，由于非饱和膨胀土的膨胀压力随含水量和吸力的变化而变化，产生异常升降运动，给结构的正常使用带来巨大安全隐患。

近70年来，膨胀土胀缩体积变化的预测研究取得了很大进展，土体膨胀潜势的预测方法主要有：经验法[1]、固结仪法[2]和基质吸力法[3]。B.H.Rao等[4]、S.Vanapalli等[5]、S.K.Vanapalli等[6]总结了预测土壤膨胀潜势的方法，发现土体达到饱和时的最大膨胀潜势在工程中有重要意义。然而，由于环境变化[7]或其他因素[8]引起的土壤水分变化对土壤运动随时间的变化和强度也有着显著影响。因此，土体随时间变形的研究对膨胀土地基的可靠设计和膨胀土预润湿及控制润湿方案的评价都具有实用价值。

固结仪法因其操作简单易行，是室内测试膨胀土的变形时效特性的常用方法。然而由于其测试周期较长，费时费力，最近20年来，众多学者针对其变形时效性展开理论研究，J.Briaud等[3]提出，任何预测膨胀土变形时间效应的方法均包括基质吸力随时间的波动幅度和非饱和膨胀土本构方程两部分内容;H.H.Adem等[9]总结了膨胀土的隆起变形随时间变化的预测方法所涉及的基于固结理论、含水率和机制吸力的三类本构方程;HUNG H Q[10]基于Fredlund和Morgenstern建立的体积变化本构关系,提出了一种膨胀土随时间变化的理论方法，通过饱和-非饱和土体水流分析，估算土体截面基质吸力的变化，然后利用基质吸力的变化进行应力-变形分析，从而预测土体随时间的隆起。该方法的关键是三维本构面(孔隙比、正应力、基质吸力)的获取，由于传统实验室一般不具备基质吸力试验条件，而且这类实验通常昂贵且费时，因此在工程实践中难以推广。

H.H.Adem等[11]基于弹性模量法提出了估算土体隆起随时间变化的预测方法，结合计算土体与环境模型的VADOSE/W(Geo-Slope)软件对非饱和土体的结构本构关系进行综合分析，并且获得了理想的结果。由于弹性模量与基质吸力模量的关系是基于饱和土体假设并应用于非饱和土体中，因此与实际情况有一定出入。众多学者对膨胀土的起伏潜势展开研究，然而，关于土体吸水变形时效分析的各种方法均存在各种不足。

本文从膨胀土的渗透吸水试验角度出发，总结土体的湿化隆起与含水率、干密度和变化时间效应，基于试验结果的半经验规律和数值分析技术相结合，提出一种膨胀土湿化变形随时间变化的半经验本理论研究方法。结合Geo-Studio 2018R2 SEEP/W模块研究非饱和膨胀土中水分的运移规律，计算膨胀土的吸水变形随时间变化半经验曲线关系。

1 室内试验

1.1 试样制备与试验

本次试验基于固结试验仪和滤纸法测量土体的无荷载膨胀率和基质吸力。试验用土选自贵州省贵定县境内尖山营特大桥周边的灰白色膨胀土，其物理性质如表1所示。

表1 膨胀土的物理性质

设计试样的干密度为1.4～1.78 g/cm3，初始含水率为8.5%～32%，标准环刀试样的干密度含水率和自由组合，试样个数共设计41个，在固结仪上依据《土工试验方法标准》(GB/T 50123-1999)开展系统试验，获得不同初始条件下的无荷载膨胀率。

为便于后续数值模拟的参数选取，采用滤纸法对干密度为1.6 g/cm3、初始含水率为5.7%～27.9%的环刀试样开展基质吸力试验，如图1所示。两个环刀试样之间放置3张直径5 cm的双圈牌滤纸，用防水胶带密封闭合，放置到密封隔离瓶中，试样顶部放置支架和2张滤纸，用于测试基质吸力和总吸力。在自制恒温箱中，保持温度在28 ℃，持续两周。之后，取出滤纸测试吸水量，并采用率定曲线[12]计算基质吸力。

图1 基质吸力试验过程

1.2 试验结果与分析

1.2.1 无荷载膨胀率实验

试样在固结仪中的吸水渗透模式如图1所示，水分从试样底部穿过透水石与土体相接触。试样渗透吸水产生变形，典型无荷载膨胀率δ随时间变化的曲线和位置关系如图2所示，土体吸水6 h左右，试样膨胀率趋于稳定。

图2 膨胀率-时间关系

对所有试样的膨胀率数据与其对应的初始含水率和干密度进行数值模拟，如图3所示。纵、横坐标之间满足多项式拟合

(1)

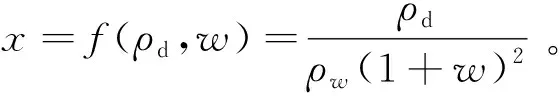
(2)

图3 最大膨胀率与初始含水率、干密度的关系曲线

取多项式的前3项时，拟合度大于0.9，考虑计算的简便性和准确性，仅取式(1)的前3项。由式(1)～(2)可得，试样吸水饱和后的膨胀率与初始含水率、干密度之间的关系式满足

(3)

式中:a0=111.845,a1=-157.32,a2=57.402,均为拟合参数，受土体结构性及矿物成分等影响；w0为初始含水率；ρw为水的密度，取1；ρd为土体的干密度，g/cm3。

试样完全渗透后，饱和含水率与初始含水率、干密度之间的关系如图4所示，满足幂指函数关系：

(4)

整理式(4)，得饱和含水率与初始含水率、干密度之间的函数表达式

wsat=b1(w0ρd)b2-1(1+w0ρd)b2，

(5)

式中：w0为初始含水率，%；干密度ρd的取值同上，其他取值见图4。

图4 饱和含水率与初始含水率、干密度的关系散点图

结合已有研究[13-14]，在无荷载状态下，土体的一维无荷载自由膨胀率满足

δ=alnw0+b，

(6)

式中：δ为无荷载膨胀率，%；w为吸水膨胀的过程含水率，%；a，b为拟合参数，与土体的初始含水率和干密度有关。

根据边界条件，w=w0时，δ=0；w=wsat时，δ=δsat，即

aln (w0)+b=0，

(7)

aln (wsat)+b=δsat。

(8)

由式(7)～(8)可得a,b的表达式

(9)

将式(9)代入式(6),可以得出土体试样的无荷载膨胀率与过程含水率的关系式

(10)

基于土力学基本公式可知，土体的质量含水率w与体积含水率θ之间满足关系式

θ=ρdw。

(11)

实际计算中，由于不同位置土体渗透吸水先后有顺序，将给定的计算土体剖面划分为若干(n)层，将不同第i层土的一维膨胀率与对应层厚(Δhi)相乘，可计算出该层厚吸水的膨胀量，膨胀土剖面的总隆起量是活动区内各层隆起量的总和，即

(12)

将式(3)、(5)、(10)～(11)代入式(12)可得，土体渗透吸水变形量与含水率、干密度以及体积含水率有关的表达式为

(13)

式(13)为由试验获得的一定厚度的膨胀土渗透吸水一维膨胀量经验计算公式。当材料参数(初始含水率、干密度)一定时，土体的湿化变形量是关于过程体积含水率的函数。

1.2.2 基质吸力试验

采用Fredlund-Xing(1994)模型可得不同类型土壤的土-水特征曲线(SWCC)，见图5。土体的体积含水率与基质吸力之间的关系式[15]为

(14)

式中:ψr为进气值,kPa；θs为饱和体积含水率；其他各个拟合参数的取值见图5。

本试验结果验证了Fredlund-Xing(1994)模型的准确性。

图5 土-水特征曲线

2 有限元过程模拟

2.1 渗流计算理论

渗透吸水作用下土体随时间变化为双向耦合过程。膨胀变形过程中，水的流速控制着超孔隙水压力的耗散并引起变形，而超孔隙水压力的产生与土体骨架对变形的抗力有关。因此，采用SEEP/W和SIGMA/W的组合模拟耦合变形。渗透过程中，饱和与非饱和区域的改变是动态变化的，此时质量流入和流出土体的变化率必须等于土体内质量的变化率，同时液态水在机械能梯度作用下的质量流量符合变密度流体的Darcy定律，将Darcy定律和质量守恒定律相结合，二维饱和—非饱和的渗流控制方程[16]为

研究表明，土-水特征曲线与非饱和土的性质之间存在关系[17]，可利用饱和渗透吸水和土水特征曲线预测非饱和土的渗透系数方程[18]，水力传导率的表达式方程为

Kw(ψ)=Ksat[1-(a′ψ)n-1(1+(a′ψ)n)-m]2÷

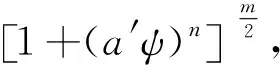
(16)

式中：Ksat为饱和土的渗透系数；ψ为基质吸力，kPa；拟合参数a′=1/a，参数m,n,a的取值同Fredlund-Xing(1994)模型。

式(15)～(16)为SEEP/W中体积含水率、孔隙水压力关于时间的关系。假设水密度在时空上是恒定的，结合质量守恒和Darcy定律，忽略水汽传递和热膨胀，常规的地下水流动方程[18]

(17)

式中，β为土体的结构压缩系数。式(17)描述了土体结构的孔隙水压力变化。

土体的体积变形服从D.G.Fredlund等[19]提出的土体结构本构模型

将土壤结构的体积应变关系(式(18))与孔隙水压力变化(式(17))联系起来，便可获得土体的体积变形随孔隙水压力的变化关系。

2.2 计算参数与边界条件

软件中应用了基质吸力模拟和土壤隆起预测两个步骤，考虑瞬态等温分析的二维问题，建模求解了地表水与能量平衡、地下热传导和变饱和流动的方程组。吸力模拟的边界条件如图2所示。在计算期间，沿底部边界保持0.03 m的压力水位。土体的初始孔隙水压力为-900 kPa，对应于土体的初始含水率9.5%和干密度1.46 g/cm3。试样的材料属性使用软件的估计值，如图6所示。

图6 膨胀土土-水特征曲线与渗透函数曲线

2.3 计算结果

由图7可知，试样在水平方向上的体积含水率完全相同，当吸水54 min后沿着试样轴线方向的体积含水率与距离呈指数函数分布，水从下往上渗流，试样底部首先吸水并达到饱和含水率状态，向远离底部方向体积含水率逐渐减小，这与实际渗流情况一致。

图7 渗透吸水54 min后的含水率分布图

由图8可知，沿着试样轴线方向，试样顶部最后吸水至饱和，3 h内，试样的所有位置均达到饱和状态。图9中在模拟过程中，不同时刻试样I-I′剖面随入渗的变化情况，说明前述入渗对土体体积含水率的影响。

图8 体积含水率-时间的关系

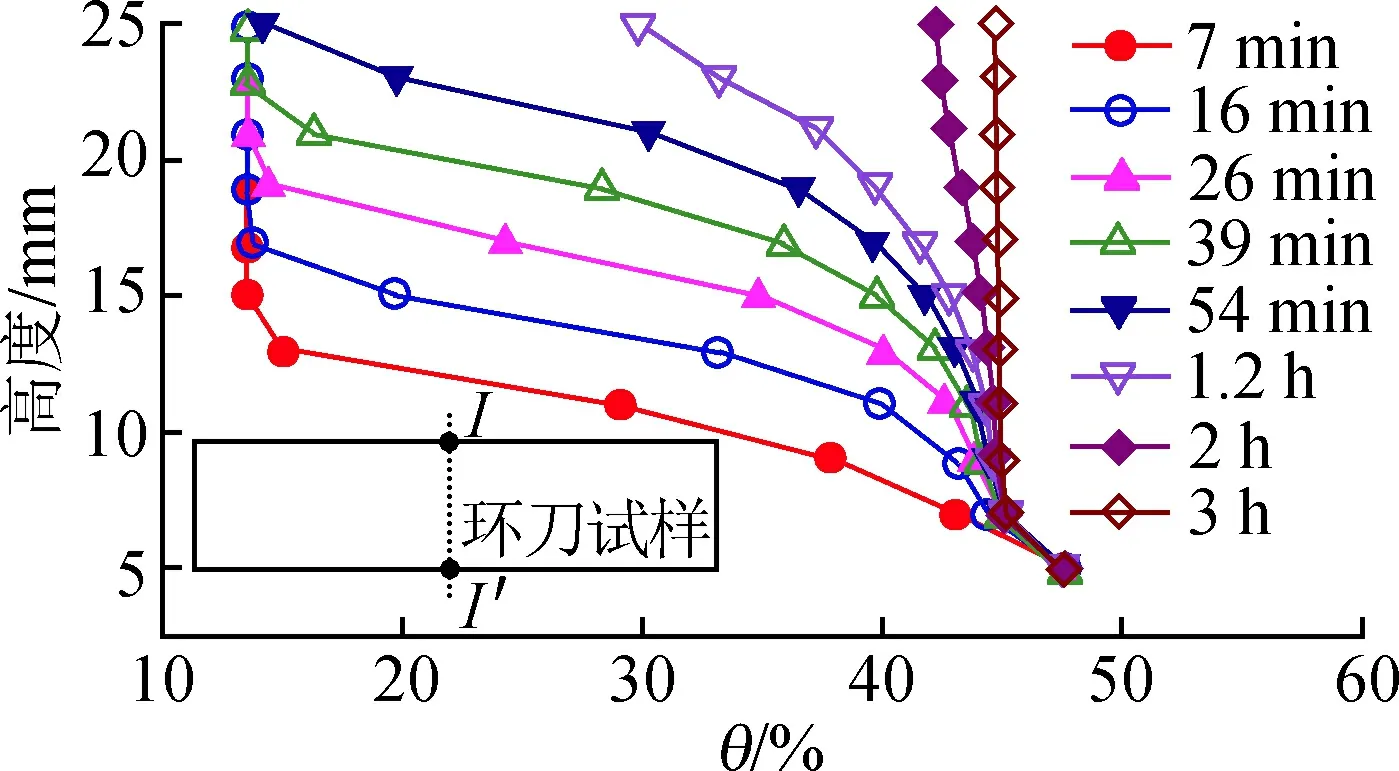
图9 3 h内试样20 mm剖面内体积含水率分布

根据土壤剖面中基质吸力随时间变化的估算值，可计算任意深度下的一维总升沉量。

2.4 对比与分析

根据土壤剖面中体积含水率随时间变化的估算值，将试样分成5层，每层厚4 mm，应用式(13)计算任意深度下的一维总升沉量，进而获得试样测试位置(图2)的吸水膨胀量，与室内实测值作对比，如图10所示，在具有相同的初始含水率和干密度条件下，计算值与试验测试结果拟合度较好。另外，应用Geostudio软件体积变形模块计算膨胀量随时间的变化过程同样与测试值之间高度一致。对比发现，计算值较测试值偏高，软件模拟值较试验值偏低，经验计算值偏高的原因可能是采用了一维计算，而实际试样内部产生的是二维复杂耦合变形；软件计算值较测试值偏低的可能原因是模拟中应用的弹性模量是固定值，实际吸水膨胀时试样的弹性模量是变化的。数值模拟和经验计算均能将试样吸水的变形时效性趋势呈现出来，从实际工程中的保守计算角度考虑，本文提出的计算值相对较合理。

图10 测试值与计算值的对比

3 试验验证

以H.Q.Vu等[20]关于膨胀土层的一维隆起预测的研究为例，检验本文半经验方法的可靠性。计算模型为厚5 m的地层，上部结构为轻质薄板，降雨强度为1.73 mm/d时，降雨入渗，分别计算薄板右侧附近距离地表0 m(A点)、1.5 m(B点)和3.5 m(C点)位置处的隆起量。计算过程中涉及的材料各参数如表2所示。

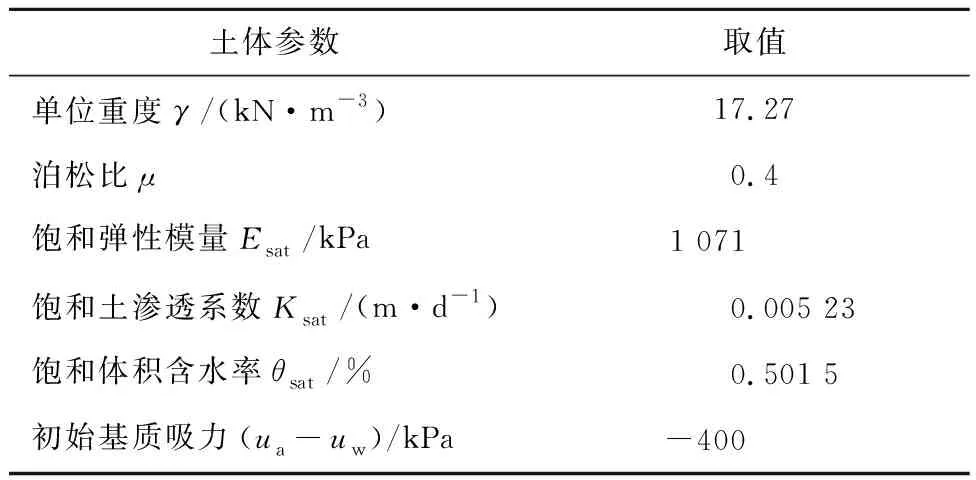
表2 土体计算参数表

土水特征曲线和水力传导率曲线同H.Q Vu等[20]和H.H.Adem等[11]文中的曲线。由初始基质吸力值与SWCC可知,案例中土体的初始体积含水率为0.379；由土体的单位和土体力学基本公式可知，初始干密度为1.34 g/cm3；由土体的饱和含水率和初始体积含水率代入式(13)可得出，分母部分取值为0.28，而由式(5)计算出的式(13)中的分母部分为0.31，两者基本一致。

由于式(3)中a0,a1和a2取值受到土体矿物成分影响。当a0=111.845,a1= -157.32,a2= 57.402时，土体最大膨胀率为5.38%，此时隆起量-时间关系曲线较H.Q.Vu等[20]的值偏小，说明案例中的膨胀土胀缩特性较本文研究对象明显，即吸水膨胀率更大；本案例中a0=113.845，a1= -157.32，a2= 57.402时，δsat=7.5，计算值与H.Q.Vu等、H.H.Adem等计算值对比,如图11所示。

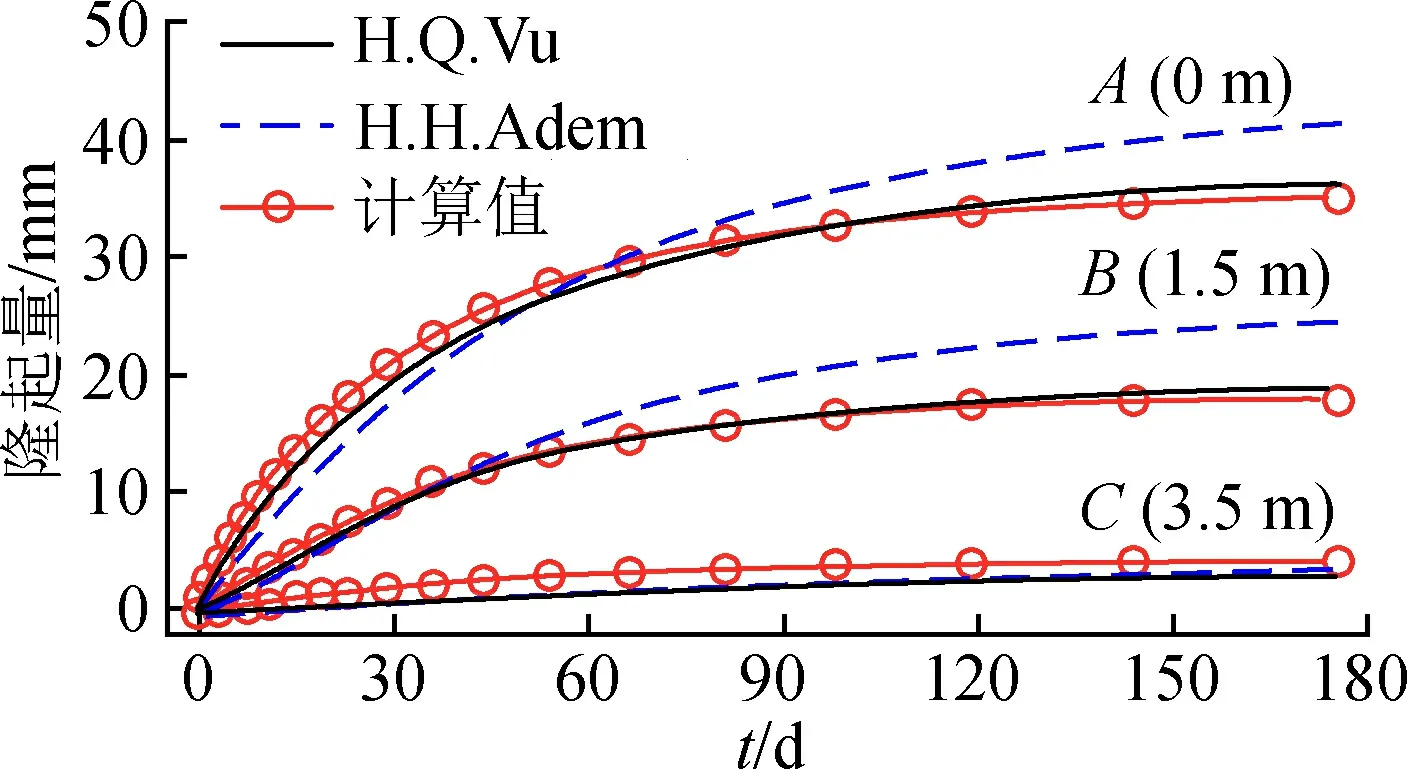
图11 采用经验计算、MEBM和H.Q.Vu 方法的隆起预测值曲线

对比发现，半经验计算值与H.Q.Vu等、H.H.Adem等的方法计算结果趋势相同，且本文提出的方法与H.Q.Vu等的拟合度更高，说明半经验计算理论可应用于膨胀土的一维隆起预测。同时说明，影响膨胀土体隆起量的关键参数是土体的最大饱和膨胀率，本文建立的饱和膨胀率计算公式理论上仅适用于贵州贵定膨胀土，对于其他类型土体膨胀率求解公式中拟合参数则需做适当调整。

4 结 论

(1)重塑膨胀土吸水膨胀6 h左右时，膨胀量达到总膨胀量的90%，之后趋于稳定。吸水饱和后的膨胀率与土体的初始含水率、干密度之间呈复合多项式关系；饱和含水率与初始含水率、干密度之间呈复合幂指函数关系。

(2)通过试验规律和理论分析可知，试样吸水过程中的膨胀量与对应时刻和位置的含水率之间存在函数关系。

(3)滤纸法获得土体的基质吸力与体积含水率的关系用Fredlund-Xing(1994)模型拟合，高度一致，验证了Fredlund-Xing(1994)模型的正确性。

(4)半经验公式与SEEP/W软件相结合，计算分析可知，土体膨胀量随时间变化与室内测试值一致高度。通过案例应用检验了该半经验方法的可靠性，说明本文提出的与有限元相结合的经验计算公式可应用于膨胀土的一维隆起预测，精度满足工程实践的需要。鉴于本文并未考虑膨胀土的裂隙性对变形的影响，这一部分还有待进一步研究。