横向滚花装配凸轮轴连接强度理论分析与实验研究

刘俊利，焦豪奇，关洪涛，张青华，王华伟，闫艳燕

(1.河南理工大学 机械与动力工程学院，河南 焦作 454000；2.河南中轴控股集团股份有限公司，河南 焦作 454000)

0 引 言

装配式凸轮轴是将轴管、凸轮、轴颈和法兰端头等零部件按各自的性能要求分别选材加工，然后通过不同的连接方法装配于一体的[1]。与传统凸轮轴加工方法相比，装配式凸轮轴兼有材料匹配灵活、结构紧凑、精密化、轻量化、低成本、低能耗等优点，并且便于实现凸轮轴生产过程的柔性化、自动化和智能化[2-3]。其中，横向滚花连接能够实现常温下局部滚花变形，对轴管与凸轮的加工精度要求较低，能在一台设备上完成自动上料与装配，具有较低的设备采购及维护成本，是凸轮轴生产厂家的首选方案[4]。但是横向滚花凸轮轴生产中涉及的加工制造参数较多，目前的研究多数是从单一参数变量对连接强度的影响进行分析，没有具体理论计算公式以阐述每一个参数与连接强度之间的关系[5-7]。企业开发新产品时需要凭借经验和不断实验以确定各个加工制造参数，实验周期长、试制成本高。本文通过对横向滚花连接装配过程和失效形式进行分析，推导出横向滚花连接静扭矩的计算公式，以期为各部件加工参数的确定提供依据。

1 横向滚花连接强度分析

1.1 装配关系的力学等效模型

装配过程中，凸轮的内孔花键将轴管上的齿峰剪切或挤入齿谷，形成异型材料镶嵌和不连续圆柱面过盈装配，这两部分是动态变化和相互影响的。为简化该装配模型，将该过程简化为剪切轴齿和过盈装配两个相对独立的过程。装配完成后，内孔键槽与轴齿镶嵌形成类花键连接，凸轮内孔与轴管表面形成过盈连接，如图1所示。横向滚花凸轮轴承受的扭矩简化为2个部分：由异材镶嵌形成的类花键连接力矩和过盈装配产生的摩擦力矩，如式(1)所示，

T=T′1+T′2，

(1)

式中：T为横向滚花凸轮轴承受的扭矩；T′1为横向滚花类花键连接承受扭矩，N·m；T′2为横向滚花过盈连接承受扭矩，N·m。

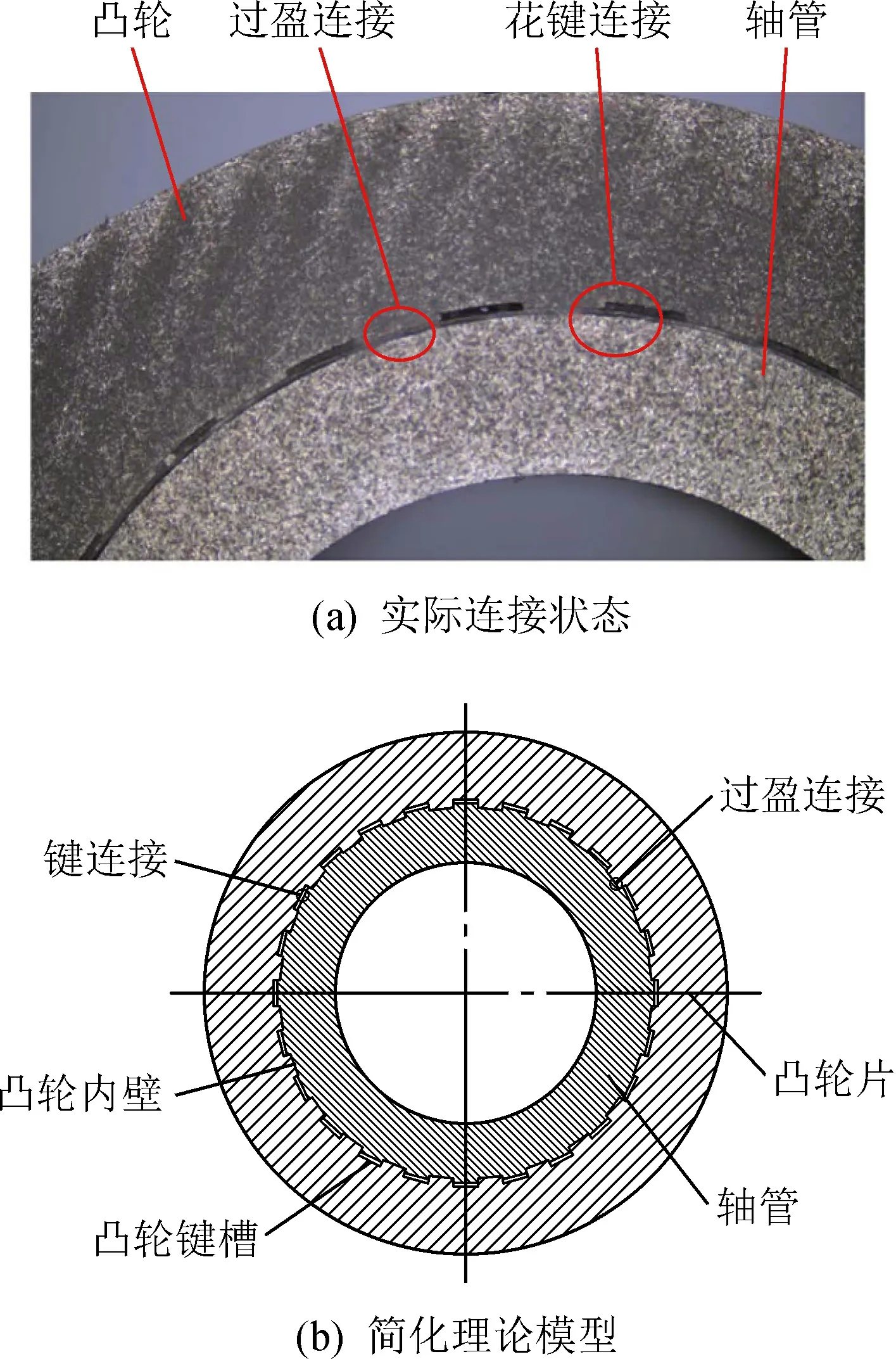
图1 装配完成后连接状态

1.2 基于异材镶嵌的花键连接强度分析

横向滚花连接凸轮材料的屈服强度和硬度比轴管材料高，装配过程中轴管被凸轮内孔花键剪切出齿槽,形成异型材料镶嵌连接，如图2所示。可以将其简化为花键连接，按照花键的压溃强度进行计算与校核。

正常花键联接强度进行计算时，假定载荷在花键的工作面上均匀分布,单齿工作面上压力的合力F作用在平均直径dm处，传递的转矩为[8]

(2)

式中：T1为正常花键连接承受力矩,N·m；Z为花键齿数；F为单齿工作面上压力的合力，N；dm为花键的平均直径，mm。

图2 装配后轴管和凸轮状态

引入系数Ψ表示实际载荷在各键齿上分配不均的影响，花键连接所能承受的应力不大于较弱材料的许用应力，即

(3)

式中：σH为工作齿面所受的应力，MPa；Ψ为载荷分布不均匀系数；l为齿的有效工作长度，mm；h为花键齿侧面的工作高度，mm；[σp]为花键连接的许用挤压应力，MPa。

横向滚花凸轮轴的花键连接是由凸轮剪切轴管上的螺纹形成的，由于螺纹上有齿峰和齿谷，花键连接侧面接触长度并不等于凸轮的厚度，因此需要引入修正系数K1，则

(4)

式中，K1为花键侧面接触系数，取值与齿形和过盈量有关。

1.3 基于弹性摩擦的过盈装配连接强度分析

横向滚花装配的过盈连接可以简化为厚壁圆筒过盈连接进行受力分析，如图3所示[9-10]。只传递扭矩时扭矩计算公式为

(5)

式中:T2为过盈连接传递的扭矩，N·m；P为最小径向压力，MPa；d为配合公称直径，mm；l为配合长度，mm；f为配合面间的摩擦系数，f=0.1～0.12[11-12]。

影响涉水领域“两法衔接”机制有效构建的关键瓶颈，既有水行政执法信息共享机制不健全、涉水刑事实体立法空白等制约因素的限制，也有证据转化和移送监督制度不完善等制度性约束。

横向滚花装配的装配过盈量比较大，接触面发生了弹塑性变形，根据参考文献[13-14],接触面处的径向压力为

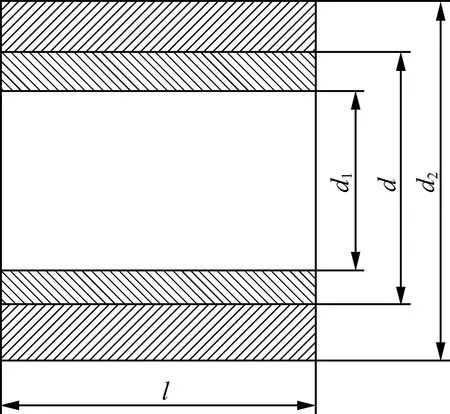
图3 厚壁圆筒示意图

(6)

(7)

(8)

式中：C1为被包容件的刚性系数；C2为包容件的刚性系数；d为配合的公称直径，mm；d1，d2分别为被包容件的内径与包容件的外径，mm；μ1，μ2分别为被包容件与包容件材料的泊松比；δ为过盈配合连接的过盈量，mm；P为配合面间所需的最小径向压力，MPa;E1，E2分别为被包容件和包容件材料的弹性模量，MPa。

图4 压入法装配时配合表面擦去部分示意图

当采用压入法装配时，配合表面的微观峰尖被擦去或压平一部分，如图4所示，此时过盈量应考虑被擦去的部分，如式(9)～(10)所示。

δ=Δ+2(S1+S2)，

(9)

Si=1.6Rai，i=1,2，

(10)

式中:Δ为理论过盈量;S1，S2分别为被包容件和包容件表面被擦去或压平的深度，mm；R，ai分别为被包容件和包容件配合面粗糙度轮廓算术平均偏差，mm，其值随表面粗糙度而异。

图5 实际接触长度

图6 影响参数K2示意图

横向滚花过盈连接是轴管剪切变形后露出的新表面与凸轮内孔的过盈接触，不是连续的圆柱面，如图5所示。实际接触面积和滚花的齿形和装配过盈量有关系，需要引入修正系数K2，K2的取值与齿形、过盈量等参数有关，如图6所示，计算公式为

(11)

式中：K2为实际接触长度修正系数；L为滚花齿宽，mm；L1为装配完成后接触长度，mm；H1为装配过盈量，mm；H为齿高，mm。

将式(4)和式(12)代入式(1)，得到横向滚花连接能够承受的扭矩T的理论计算公式，即

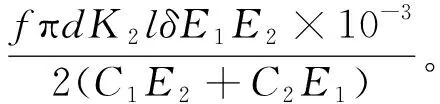
(13)

2 装配及扭转过程的有限元分析

2.1 装配过程的有限元模型建立

在实际生产中，某发动机凸轮轴扭矩要求为80 N·m，为了验证和优化理论计算公式(13)，根据设计经验及理论推导公式,设计出轴管和凸轮参数如表1和表2所示，材料参数如表3所示，理论计算扭矩T=406.8 N·m。

表1 轴管加工参数

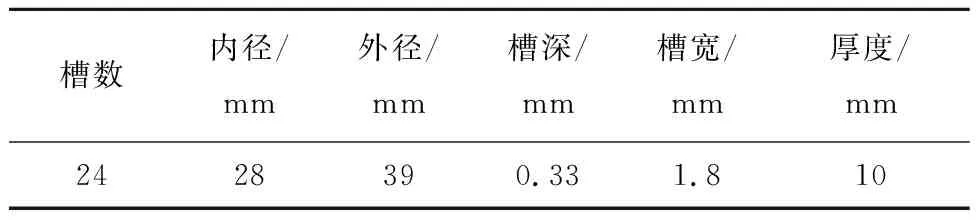
表2 凸轮加工参数

表3 凸轮及轴材料参数

根据设计的各加工制造参数建立三维模型，运用ABAQUS软件进行装配和扭转过程仿真分析。装配和扭转过程涉及到材料切除、塑性变形等问题，被切除材料45号钢的塑性参数如表4所示[15-16]。

表4 45号钢的Johnson-Cook参数

横向滚花连接装配过程及装配后的轴管连接状态对承受扭矩的大小影响很大，为了使仿真分析更接近实际转动破坏情况，采取整体模型在大型工作站上仿真。划分网格时轴管滚花部位和凸轮内孔拉槽部位是剪切破坏、塑性变形、过盈配合等相互作用的主要发生区域，网格需要细化，设置参数为0.08；轴管靠近内孔部位及凸轮靠近外表面的部位受力很小，网格划分得比较大，设置参数为0.8，并避免出现网格畸变。

2.2 装配及扭转过程分析

装配过程动态分析(装配力)：凸轮外表面设置固定约束，将轴管上表面耦合到中心点，设置恒定速向轴管运动。装配及扭转过程中轴管的应力如图7～8所示，装配完成后剪切形成新面与凸轮内孔形成过盈配合。

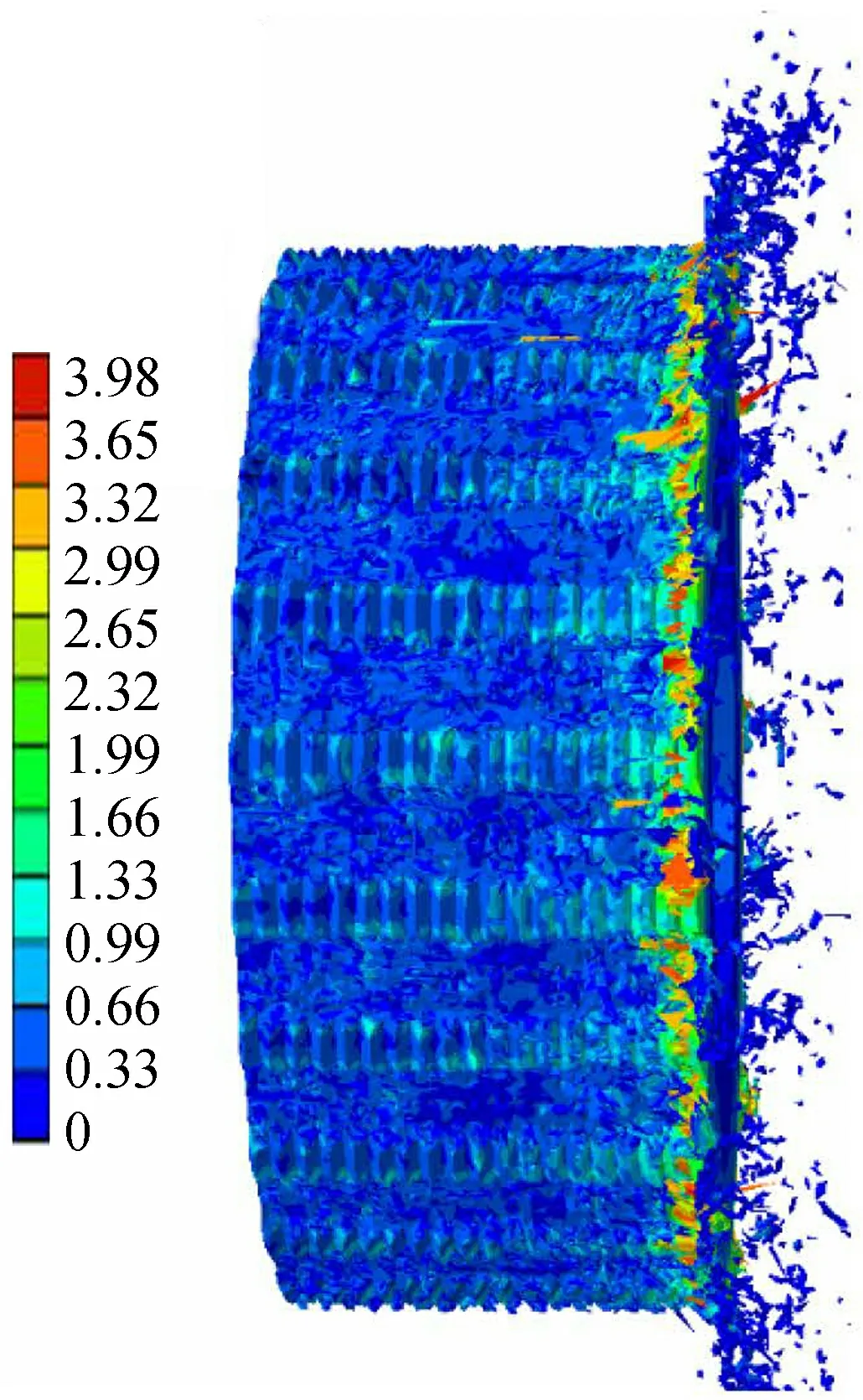
图7 装配过程轴管应力

图8 扭转过程轴管应力

静态破坏扭矩：固定约束设置为传递，匀速运动设置为未激活，对上表面耦合点设置转动角速度，凸轮和轴管发生一定角度的相对转动。随着角度的增加，扭矩升高到最大值485.96 N·m，之后在320～490 N·m间起伏，最后下降到5 N·m附近，连接完全失效，如图9所示。仿真结果比理

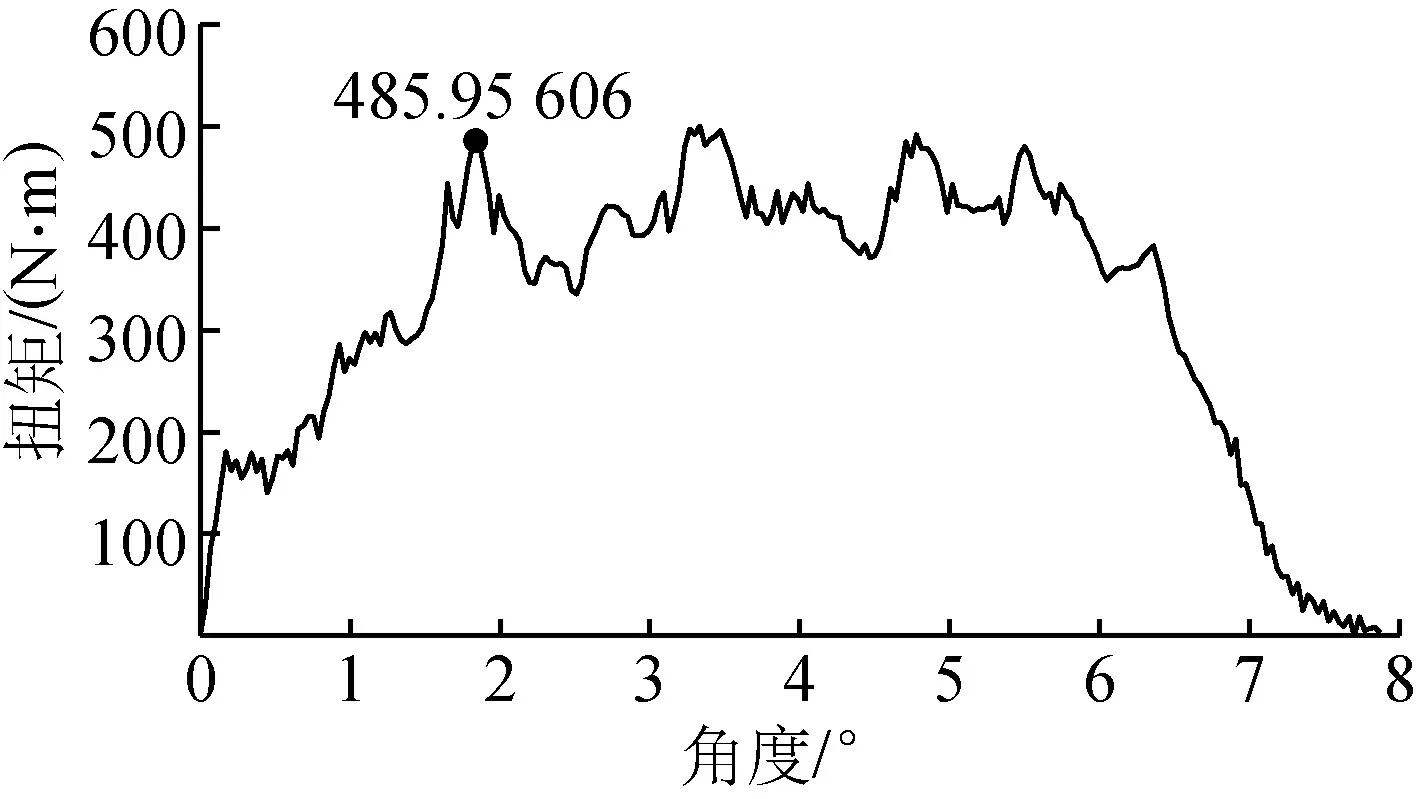
图9 扭矩仿真数据

论分析的最大扭矩要大一些，一方面仿真是完全按照理想的状态进行计算的,没有考虑到接触不均匀等影响因素；另一方面被切削材料一部分填充到滚花的齿底部分和凸轮形成摩擦副,也能够承受一定的扭矩。

3 同参数装配后的扭矩实验分析

按照理论计算及仿真模拟结果，确定满足发动机扭矩要求的轴管与凸轮参数，加工制造轴管与凸轮并利用某公司数控装配平台完成滚花和装配工作。凸轮轴破坏扭矩的测定需要对凸轮进行固定，同时对轴管施加扭矩，随着扭矩的增大，凸轮与轴管发生相对转动，连接失效，将发生相对转动时扭矩作为凸轮轴能够承受的最大扭矩。实验室的扭矩实验平台是测试杆状材料扭转强度的实验设备，可以检测装配凸轮轴连接强度，由于凸轮特殊的轮廓形状，需要设计专用夹具对实验平台进行改造，如图10所示。通过扭矩测试软件设定旋转角速度,使凸轮一端匀速转动,同时记录旋转角度和扭矩的大小。工作原理如图11所示。

图10 扭矩实验平台

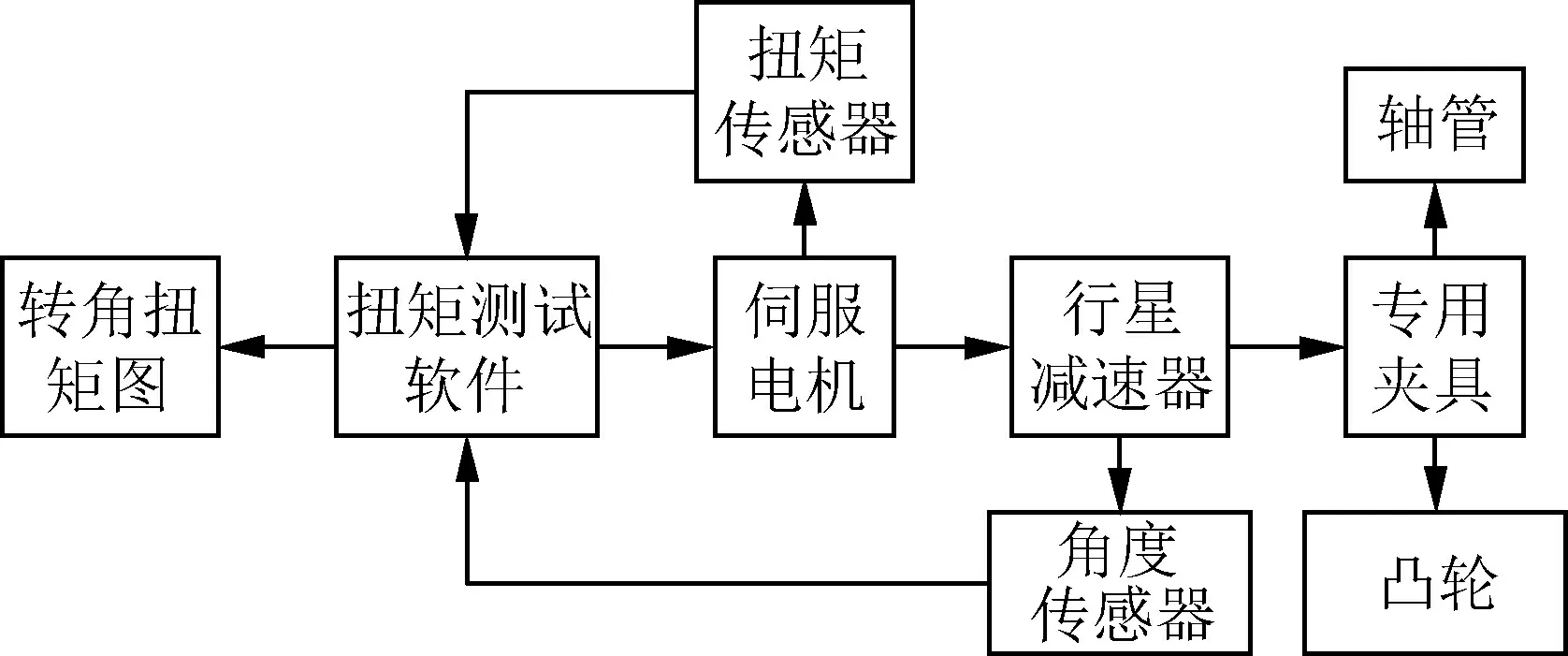
图11 扭矩实验工作原理

对同一横向滚花连接凸轮轴上2组凸轮进行扭矩破坏测试，得到的2组实验力矩随角度变化的趋势一样：经过配合间隙的很小角度之后,扭矩随着转动角度迅速增大,达到最大值，随后扭矩迅速下降,最终扭矩在110 N·m附近震荡，如图12所示。

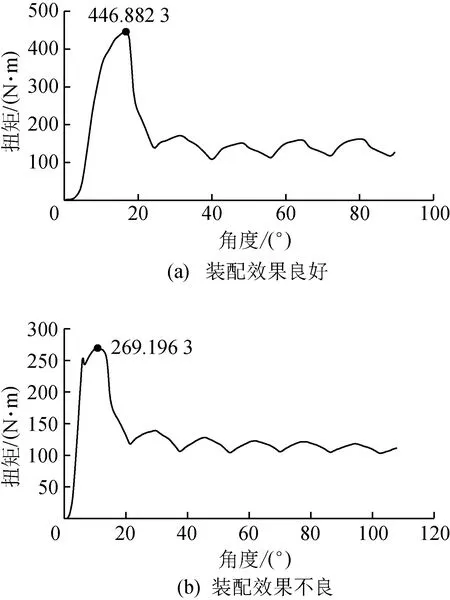
图12 扭矩实验数据

由图12可知，两组静态破坏扭矩相差较大，其原因是：凸轮和轴管加工制造过程存在误差，装配过程中滚花成型效果不理想造成滚花高度不够，装配后没能形成理想的类花键结构，如图13所示；轴管与凸轮不同心等因素对横向滚花连接静态破坏扭矩影响很大，如图14所示。为了减小静态破坏扭矩浮动区间，在设计阶段应当对轴管外径和凸轮内孔尺寸设置合理的公差范围，在滚花和装配阶段提高装配设备精度，这也是目前横向滚花凸轮轴制造面临的一个难题。

图13 滚花效果不良

图14 装配同心度不良

4 结 论

(1)对横向滚花连接装配过程和装配后的轴管连接状态进行了分析，横向滚花连接静扭矩失效过程可以简化为2个相对独立的部分：类似花键连接的压溃失效和厚壁圆筒过盈配合连接。

(2)根据花键连接和过盈配合2个扭矩计算公式，结合横向滚花连接实际情况引入了修正系数K1和K2，推导出横向滚花连接能够承受的最大静扭矩的理论计算公式。

(3)按照计算公式，对设计的横向滚花连接凸轮轴进行建模仿真和加工装配，然后进行破坏实验，对理论计算的破坏静扭矩进行了验证。结果表明：仿真和实验的连接失效过程与理论分析的连接失效过程相吻合;数值上理论计算结果比实验结果低8.97%，仿真结果比实验结果高8.74%。根据仿真和实验结果，针对不同齿形可以对系数K1，K2优化，从而减小理论计算误差。

(4)研究结果表明，可以采用理论计算确定加工工艺参数，运用模拟仿真进行优化，最后通过实验验证的方法进行新产品设计，从而减少设计工作量和设计成本，缩短产品的研发周期。