凹穴型微通道液-液两相流动特性
2021-01-20李慧玲赵玉婷周乃香张井志
雷 丽, 李慧玲, 赵玉婷, 周乃香, 张井志,3
(1. 山东大学 能源与动力工程学院, 山东 济南 250061;2. 山东省城乡规划设计研究院, 山东 济南 250013;3. 山东大学 动力工程及工程热物理博士后科研流动站, 山东 济南 250061)
1 前 言
微化工技术可以优化设备性能,降低能耗及物耗,与传统化工技术相比有明显优势[1-3]。由于装置小型化,该技术可以大幅度提高传质/传热速率,具有容易控制流态的优点[4]。微通道是微化工技术的主要组成部分,常见的流动为气-液[5-7]与液-液[8-10]两相流,而液-液两相流在硝化、萃取、聚合和药物化学等方面具有重要的应用价值[11]。液滴尺寸的精确操控是微流控技术研究的关键[12],例如 Zhu 等[13-15]、王晓军等[10]、Yao 等[8]利用实验或数值模拟的方法,分析微通道内两相流动特性。当通道壁面未完全湿润时,挤压机制向剪切机制转换的临界毛细管数减小。液滴长度与流量比呈线性关系,与毛细管数呈幂率关系。
文献中对平直微通道液滴的规律研究较多,对于复杂微通道结构的研究仍有不足。Yin 等[16]实验分析内含挡板的T 型微通道的气泡流动特性,指出流型主要有泰勒泡状流、泰勒流、破裂泰勒流。折流板微通道内气泡流经折流板区域时,经历挤压、伸长、变形、加速、甚至破裂的动态演化过程。Park 等[17-18]采用新型多级多孔分馏(multi-orifice flow fractionation,MOFF)的微流控方法,利用一系列收缩/扩张微通道中产生的惯性升力和动量变化诱导的惯性力,对不同尺寸的微球实现连续分离。Bhagat 等[19]利用惯性微流体处理稀释血液的高通量尺寸分离方法,以高吞吐量和高分辨率的优势从血液中成功分离出稀有细胞。对于扇形凹穴型微通道,夏国栋等[20-22]利用数值模拟方法指出在较大雷诺数条件下,扇形凹穴型微通道的流动与传热可归结为边界层的破坏、喷射节流效应及层流滞止区的相互作用。目前对于液滴在凹穴型微通道中,液滴的长度、形状的变化、流型的转变研究还不够深入。本文以质量分数为0.5%十二烷基硫酸钠(sodium dodecyl sulfate,SDS)的蒸馏水为连续相,硅油为离散相,分析凹穴微通道内两相液滴长度、形状及流型的变化规律,并提出凹穴型通道内流型的判定依据。
2 实验系统
如图1 所示为T 型凹穴微通道液-液两相流实验系统示意图。实验系统主要包括3 个部分:微量原料输送及废液收集系统、T 型微通道实验测试系统、数据采集系统。离散相和连续相由2 台微量注射泵(型号分别 LSP02-1B 和 LSP01-1A)驱动注入实验段。微通道采用雕刻机对亚克力玻璃平板精密加工获得,微槽道芯片与盖板通过螺栓密封连接。微通道分为两部分:长度为l1=7.5 mm 的平直段、直通道两侧间隔 l2=290 μm 加工一个 l3× h = 470 μm× 390 μm 的凹穴段。T 型微通道截面形状为矩形,截面尺寸为 W ×H = 500 μm × 415 μm,详细的尺寸见表1。高速摄像机与电脑相连,并与实验段垂直放置,通过 100 W的背光源提供所需的光照强度,用于清晰捕捉微通道内液-液两相流型。
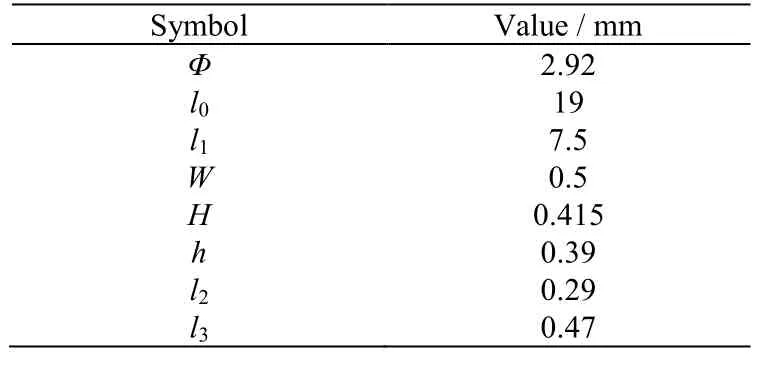
表1 凹穴型微通道结构尺寸Table 1 Structural parameters of the microchannel with reentrant cavities

图1 实验系统示意图Fig.1 Schematic diagram of the experimental setup
实验过程中,硅油为离散相,添加质量分数为0.5% SDS 的蒸馏水为连续相。流体黏度由乌氏黏度计(LVDV-II,Brookfield,USA)测量,离散相与连续相黏度分别为 μd= 0.01 Pa·s 和 μc= 0.000 92 Pa·s。连续相与离散相间的表面张力由表面张力仪(Dataphysics,Germany,DCAT11EC)获得,其值为σ = 0.011 8 N⋅m-1。本文采用矩阵实验室(Matlab)中的Canny 算法处理微通道内两相流动不同时刻的图像,获得液滴形状和液滴长度Ld。
3 实验结果与讨论
3.1 平直段内微液滴长度变化规律
本文实验中,连续相与离散相体积流量变化范围分别为qV,c= 5 ~ 200 mL⋅h-1,qV,d= 1~ 9 mL⋅h-1,平直段内对应的流型主要是弹状流和滴状流。图2 为2 种流型下液滴形成过程的示意图。由图可知,2 种流型下液滴的形成位置及形成时间有明显差异。图2(a)中液滴形成过程分为2 个阶段:填充阶段和挤压阶段[23]。对于填充阶段(t = 0 ~ 53 ms),液滴伸出长度与通道宽度相近。对于挤压阶段(t = 53 ~ 196 ms),随着离散相填充通道直至几乎占据整个通道,压差在液滴上、下游的液相间逐渐增大。当压差力的不稳定作用克服表面张力的稳定作用时,两相界面被拉伸、断裂,形成周期性的弹状液滴[13]。滴状流的形成过程如图2(b),当t = 0 ~ 17 ms,离散相占据部分通道,对连续相的流动产生阻塞作用。界面张力与剪切力对液滴破裂的作用相反,界面张力保持两相界面相对稳定。由于连续相流量较大,两相剪切力占主导作用,两相界面快速拉伸、破裂形成滴状液滴。从图(a)、(b)对比可得,弹状流的形成时间远高于滴状流。
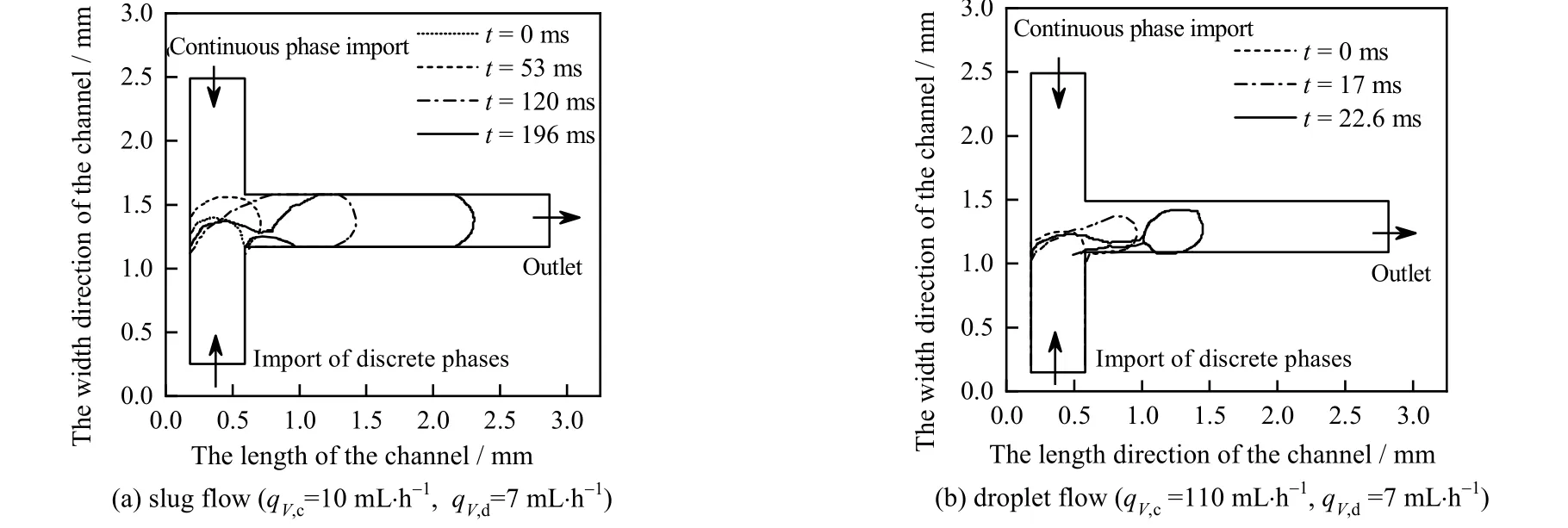
图2 液滴形成过程Fig.2 Formation processes of droplets
液-液两相流量是影响微通道内液滴尺寸的重要因素[24],液滴的无量纲长度 Ld/W 随两相流量比 q、连续相毛细管数Cac的变化规律如图3 所示。其中q 与Cac的表达式如下:

由图3 可知,Ld/W 随着q 的增大逐渐增大,随着Cac增大逐渐减小。当q 一定时,Ld/W 随着qV,d的减小而逐渐增大。对于液-液两相流来说,两相密度差所产生的惯性力作用较小,因此液滴形成主要靠表面张力、黏性剪切力及压差的共同作用。随着Cac的增大、q 的减小,液滴的形成从挤压模式逐渐转变为剪切模式,液滴的长度逐渐减小。当Cac< 0.005,Ld/W >1.5 时,通道内两相流在挤压模式下形成弹状液滴。此时Cac较小,两相之间的速度差较小,剪切力较弱。在持续增大的压差力与界面张力作用下,两相界面挤压、拉伸、断裂,形成弹状液滴。当0.005<Cac<0.01 时,通道内为过渡流。过渡模式下,新液滴会对连续相的流动产生部分或者暂时阻塞作用,液滴破裂动力从压差力与界面张力共同作用转化为压差力与黏性剪切力共同作用。Glawdel 等[25]通过实验确定了过渡阶段中,液滴形成的 3 个连续阶段:滞后、填充和收缩。后2 个阶段与挤压阶段相似,而初始滞后阶段的特征是在前一个液滴被夹断后,界面向离散相入口通道后退。
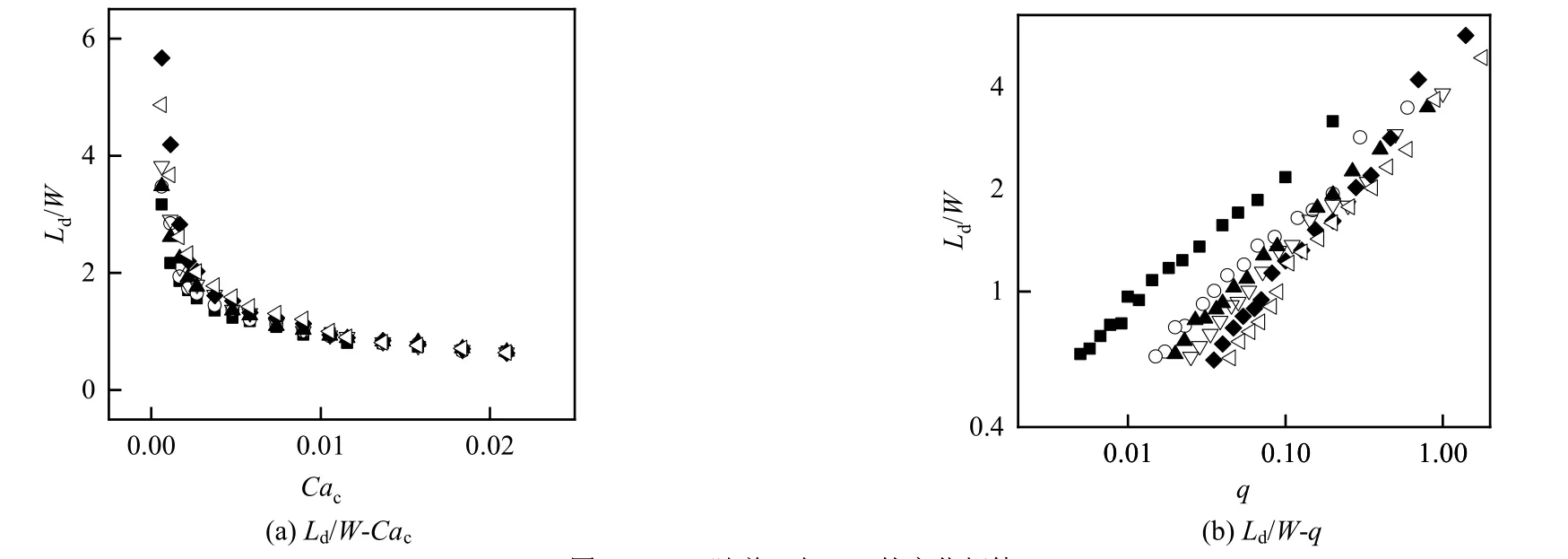
图3 Ld/W 随着q 与Cac 的变化规律Fig.3 Effects of q and Cac on Ld/W
当Cac>0.01,Ld/W<1,通道内两相流在剪切模式下形成滴状液滴。当Cac>0.01,增大qV,d对Ld/W 的影响较弱。随着 qV,c增大,连续相与离散相之间的速度差增大,剪切作用逐渐增强。当剪切力的拖拽作用足以克服界面张力的稳定作用时,离散相快速破裂形成微液滴。
3.2 凹穴段内液滴形状变化特点
图4 为3 种典型实验工况下,液滴在凹穴段内形状变化的示意图,其中3 幅图对应的直通道内Ld/W分别为3、1.8、0.8。如图4(a),当t = 0 ~ 46 ms 时,随着液滴进入凹穴通道,由于流道增大使其运动速度降低,液滴头部逐渐膨胀直至最大。在t = 46 ~ 68 ms 时,液滴经过凹穴结构时,中间区域会发生膨胀。当t = 92 ms 时,液滴的头部和尾部都处于膨胀状态。随着时间的推移,液滴形状在凹穴型结构内周期性变化。随着连续相流量的增加,液滴形状变化如图 4(b)。液滴进入矩形通道头部逐渐膨胀。在表面张力稳定两相界面的作用下,液滴逐渐膨胀为扁平的饼形。图4(c)所示,随qV,c进一步增大,液滴长度小于通道宽度。液滴通过凹穴通道时,形状基本无变化。由此可得,不同长度的液滴在凹穴型通道内形状变化明显不同。随着连续相流量的增加,凹穴通道对液滴形状变化的影响逐渐减小。液滴在凹穴型通道中不断膨胀与收缩,对周围流场起到扰动作用,对于两相之间的传质、传热起到强化作用。
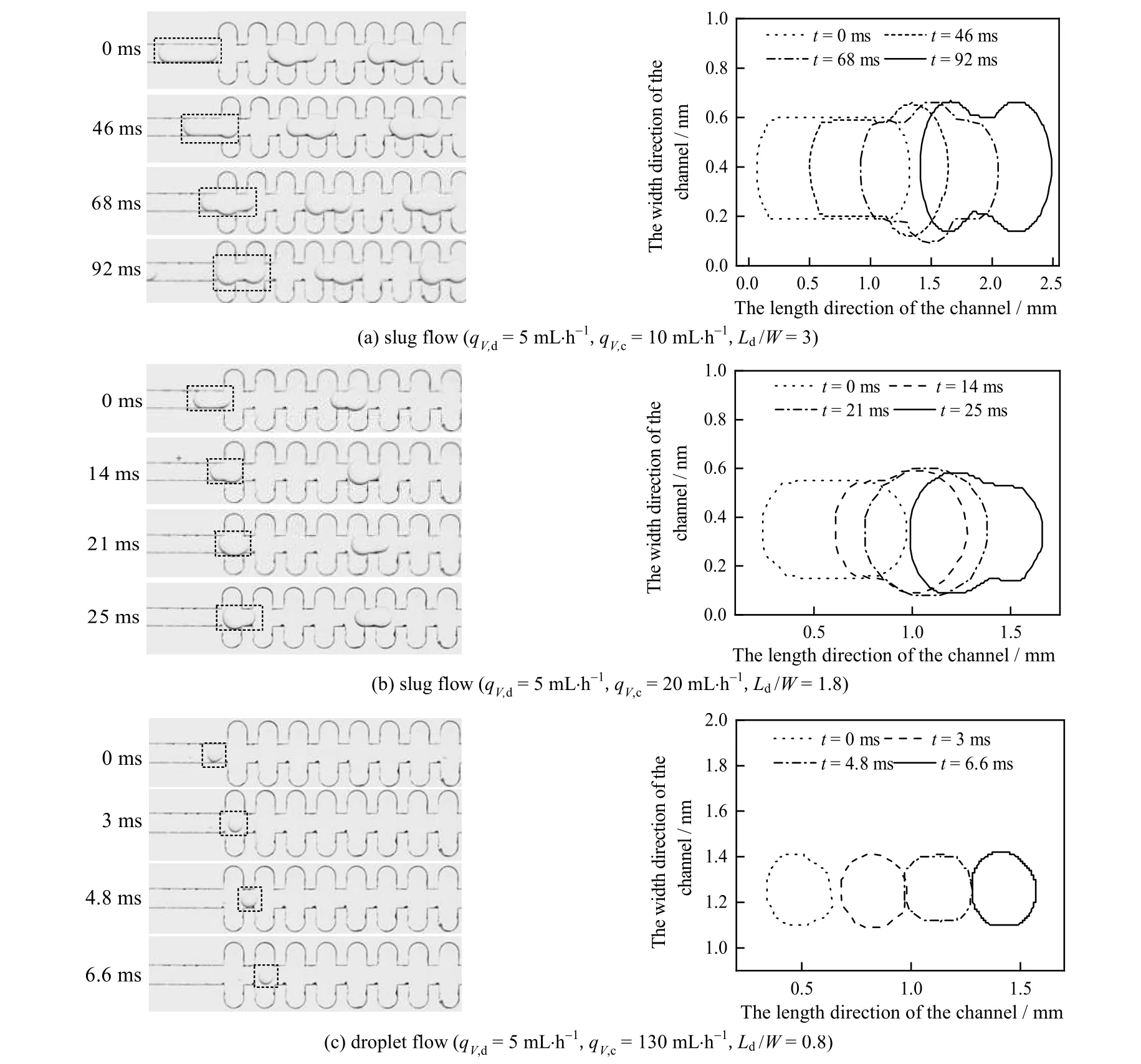
图4 液滴形状变化过程Fig.4 Evolution of droplet shapes
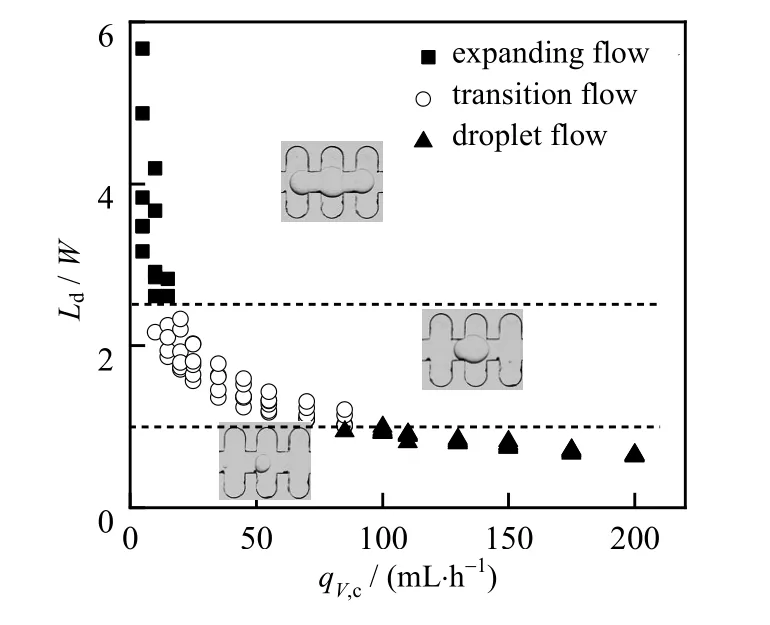
图5 凹穴型微通道流型图Fig.5 Flow patterns in microchannels with reentrant cavities
3.3 凹穴型微通道液滴流型的判定
在凹穴型通道内,液滴受通道结构的影响,不断膨胀与收缩。在离散相与连续相流量的影响下,液滴呈现不同的形状。如图5 所示,依据Ld/W 判定凹穴型通道内液滴流型,主要有膨胀流、过渡流及滴状流。当Ld/W >2.5,液滴在凹穴型通道内占据2 个及2 个以上的矩形凹穴,且膨胀现象较为明显,故为膨胀流。由于凹穴通道结构尺寸的限制,液滴在矩形通道中只能膨胀形似峰状。液滴在直通道内流动时,长度浮动范围大致为-0.025 mm< ΔLd< 0.025 mm (ΔLd:相邻两幅图像,同一个液滴长度的变化量)。当Ld/W≤1 时,矩形通道对于液滴膨胀的影响可忽略不计,通道内主要为滴状流。当1<Ld/W≤2.5,通道内流型为过渡流型。液滴在凹穴通道经过同样的头部和尾部膨胀的周期性形状变化,受限于液滴长度,液滴形状仅能出现单峰状突起。
3.4 凹穴型微通道液滴膨胀宽度和长度的变化规律
凹穴型通道内,液滴膨胀宽度的变化规律如图6 所示。ΔWd的定义如下:

式中:Wd为液滴膨胀的最大宽度,mm。
由图6 可得,ΔWd/W 随着Cac增大逐渐减小,随着q 的增大而增大。当ΔWd/W<0.25 时,随着q的减小,液滴长度变短,同时通道内液柱的推动作用增强,液滴通过扩大流道的速率增加,导致液滴膨胀程度减弱。当ΔWd/W≥0.3 时,液滴的膨胀程度取决于液滴占据凹穴型通道的长度。液滴在凹穴型通道中的膨胀形态基本一致,因此在通道宽度方向,随着 q 的增大,液滴的膨胀宽度增大速率逐渐变缓。
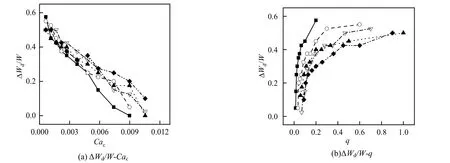
图6 ΔWd/W 随 Cac 与 q 的变化规律Fig.6 Effects of Cac and q on ΔWd/W
如图7 所示为不同通道液滴长度的变化规律,由图7(a)可知,液滴在T 型交汇处形成后,其长度在平直段内的浮动范围较小,连续相流量对液滴长度波动特性的影响可忽略。由 7(b)可知,与直通道相比,液滴在凹穴型通道内长度的变化范围相对较大,振幅为直通道的 3~5.6 倍。液滴在不断扩张与收缩的通道内流动时,长度呈现周期性变化。当qV,d为定量时,随着qV,c的增大,Ld的浮动范围逐渐减小,周期时间逐渐减少。当 qV,c较低时,通道内对应的流型为弹状流,液滴能占据 2 个及以上的扩张区域(如图4(a)所示),膨胀程度相对较大,液滴长度变化的振幅大。随qV,c的增大,液滴长度逐渐减小,膨胀程度减弱。通道内流体对液滴的推动作用随两相流量的增加逐渐增大,液滴完成膨胀与收缩的周期时间逐渐减小。
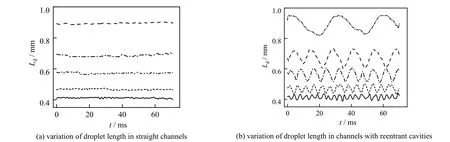
图7 不同通道液滴长度的变化规律(qV,d = 5 mL⋅h-1) Fig.7 Variation profiles of droplet length in different channels (qV,d = 5 mL⋅h-1)
3.5 凹穴型通道内液滴膨胀面积的变化规律
讨论无量纲的膨胀面积Sd/SA随两相流量比、毛细管数的变化规律。其中,Sd与SA的定义式如下:

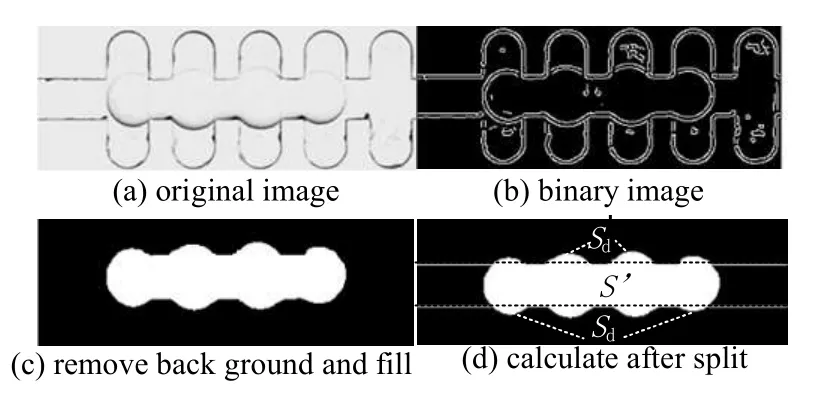
图8 膨胀面积计算方法 Fig.8 Calculation of expansion areas
式中:S 为液滴面积,mm2;S′为位于直通道内液滴的面积,mm2;SA为直通道截面面积,mm2;Sd为液滴膨胀面积,mm2。
无量纲液滴膨胀面积计算过程如图8 所示,利用Matlab 软件截取大小一致的图像,结合Canny 算法对图像进行二值化处理并填充,最后根据Sd、S′的定义将液滴分割计算得到无量纲膨胀面积参数。
如图9 所示为Sd/SA随q 和Cac的变化规律,从图中可看出,Sd/SA随q 的增大逐渐增大,随Cac的增大逐渐减小。当q 一定时,Sd/SA随着qV,d的增大逐渐减小。由图9(a)可知,当Sd/SA≈ 0.4 时,随着q 的增大、Cac的减小,Sd/SA有一个明显的跃变过程,即凹穴通道内流型由过渡流转变为膨胀流。当q >0.2 时,Cac<0.001,Ld/W >2.5,长度较大的液滴占据越多的矩形通道,液滴扩张膨胀就越剧烈。当Cac>0.001,随Cac的增大,液滴长度逐渐减小,Sd/SA随Cac的增大逐渐减小存在线性关系。当1 图9 Sd/SA 随Cac 与q 的变化规律 Fig.9 Effects of Cac and q on Sd/SA 本文通过设计微通道结构尺寸,结合Matlab 中的Canny 算法,分析了T 型凹穴型微通道结构中硅油和蒸馏水(质量分数为0.5% SDS)的液-液两相流动的液滴长度、液滴形状变化、液滴膨胀面积及流型,主要得到以下结论: (1) 滴状流与弹状流的形成机理不同,前者主要靠剪切机制作用,剪切力与表面张力起主导作用;后者受挤压机制作用,连续相积累的压差力与表面张力起主导作用。Ld/W 随q 的增大逐渐增大,随Cac的增大逐渐减小。当q 一定时,Ld/W 随qV,d的减小逐渐增大。 (2) 基于Ld/W 无量纲参数,判定凹穴型通道内的两相流型。Ld/W>2.5,凹穴型通道内的流型为膨胀流;1 ≤Ld/W≤2.5,为过渡流;Ld/W<1,凹穴结构对液滴膨胀的影响可忽略。 (3) 凹穴型通道内的液滴长度呈周期性变化,变化振幅较大。当qV,d一定时,随着qV,c增大液滴变化的振幅逐渐减小,周期变短。Sd/SA随q 的增大逐渐增大,随Cac的增大逐渐减小。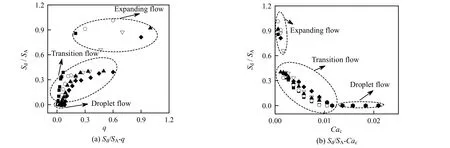
4 结 论
