航空发动机气膜浮环密封上浮性能研究*

马 也 王庆锋 施任杰 张馨宇 李庆展 李双喜

(北京化工大学机电工程学院 北京 100029)

浮环密封结构形式简单，轴向尺寸小，安全性好，在现代密封技术领域中占据重要地位。随着科技的发展,机械设备所处的工艺环境逐渐恶劣，对浮环密封性能要求更高[1]。开车前由于自重浮环内壁贴在跑道上，开车后在浮环内壁与跑道之间的楔形间隙内产生动压效应，浮环受到垂直向上的力，内壁脱离跑道[2]向上浮起。气体浮动性能相对液体来说较差，若浮环不能上浮，将会导致浮环内壁与跑道之间发生磨损甚至崩坏，严重影响密封系统的安全性，因此对浮环上浮性能的研究是非常有必要的。

国内外学者针对浮环动态运行过程做了大量的研究。为计算不同工况下动力学系数，文献[3-4]改进了浮环密封的数值模型并得到了精度更高的结果。文献[5-6]则基于雷诺方程研究了温度、槽型及变形量对浮环动力学系数的影响。HA等[7]经过有限元迭代与傅里叶变换求解了浮环的偏心率、泄漏率等密封参数，并认为浮环密封的泄漏率与动力学系数准确计算的关键在于浮环中心位置的确定。DIETZEN和NORDMANN[8]利用有限差分法得到了湍流模型的解,并利用纳维-斯托克斯方程得到了浮环密封的流场与压力场分布,进而得到了密封系统的动态系数。马利军[9]通过对高温镶装气膜浮环的节流长度以及密封径向间隙进行数值模拟以及试验研究发现，增加节流长度可以有效增加浮环内表面与流体介质的接触面积，浮环的上浮力会增大，并认为偏心率较大时浮环气膜刚度随着转速增大而增大，浮环的自我调节能力较强。

为研究浮环与跑道的振动随转速变化情况，西安交通大学浮环小组搭建密封试验台，得到了密封组件的运动轨迹图并提出了一套浮环动力学系数的理论计算方法[10]。徐庆余等[11]认为浮环的运动状态为一个二自由度非线性振动并根据短轴承润滑理论推导出了浮环油膜力的计算式与浮环轴心轨迹的计算方法,并进行了试验验证。ARGHIR等[12]研究了多因素耦合(库仑力、惯性力、转子振动等)情况下浮环的运动状态，并建立了一种更为便捷的理论分析模型。

前人研究对象大多为液膜浮环,对气膜浮环的研究较少，且对上浮转速的具体计算方法的研究较少。本文作者针对航空发动机主轴承箱的气膜浮环密封系统，建立了浮环上浮转速计算的有限元模型并搭建了试验台，分别探究了先增速后增压和先增压后增速2种开车情况下浮环各密封参数与上浮转速之间的关系。

1 工作原理和上浮过程

浮环密封是一种流阻型密封，通过石墨环内侧与跑道外侧之间的微小间隙实现节流作用。文中研究的浮环为整体式镶装浮环，浮环外侧为金属镶装环，内侧为石墨环。镶装式浮环结合了金属环与石墨环的优点，石墨环存在能够防止环与跑道发生剧烈的刚性碰撞，同时由于镶装环的存在浮环也不会轻易地发生脆性断裂。文中研究的航空发动机浮环密封组件的结构如图1所示。

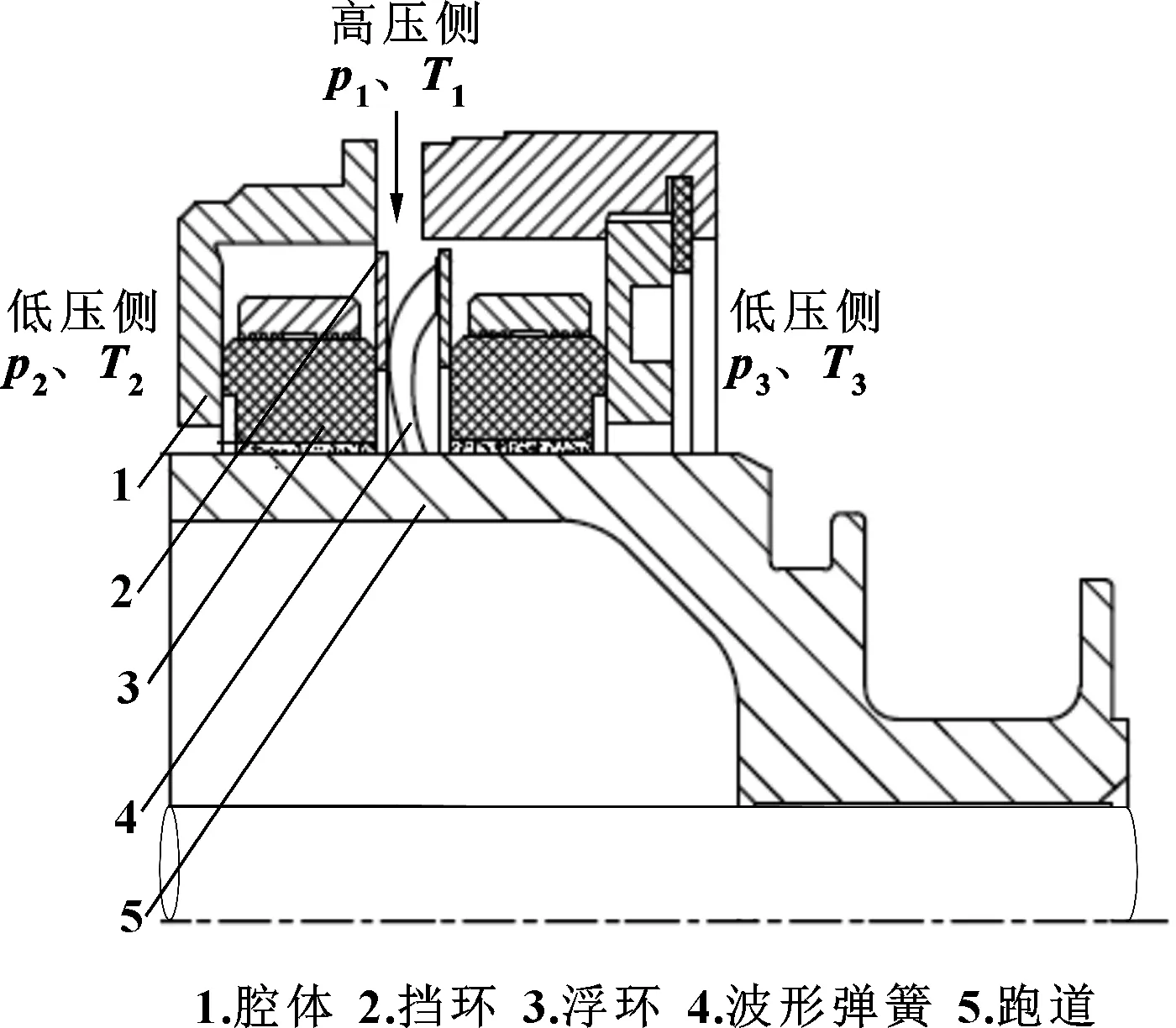
图1 浮环密封组件结构Fig 1 Floating ring seal structure

浮环上浮性能判定指标主要包括从开车到工作状态浮环能否上浮、上浮力大小、临界上浮转速的数值3个方面，当工作转速大于临界上浮转速时就认为浮环能够上浮。上浮转速主要受上浮力与上浮阻力影响，开车前浮环由于自重贴在跑道上，开车后跑道旋转，流体会对浮环产生一个向上的推力，称为上浮力。另外侧壁弹簧以及两侧压差会对浮环产生一个阻碍其上浮的摩擦力，这个摩擦力和浮环自重之和称为上浮阻力。当上浮力略大于上浮阻力时浮环就会上浮，此时的跑道的转速称为上浮转速。

2 上浮性能计算流程

2.1 上浮阻力

两侧浮环工作状态类似，文中仅对其中一个浮环进行分析。根据图1，浮环工作状态下浮环最大上浮阻力：

F=R+G

(1)

式中:F为浮环临界状态的上浮阻力；R为浮环端面摩擦力；G为浮环自重。

端面摩擦力：

R=(Fd+Fs)μ

(2)

式中：Fd为端面压紧力；Fs为波簧弹力；μ为石墨环与合金钢端面摩擦因数，取μ=0.07。

同时根据轴向方向力平衡关系，端面压紧力：

Fd=F1-F2-F3+Fs

(3)

式中:F1为高压侧工作压力；F2为低压侧工作压力；F3为侧端面气膜反力。

浮环气膜反力参考机械密封动静环间气膜反力计算，代入公式可得：

F3=p2A2+λ(p1-p2)A2

(4)

整理后可得：

F=[(p1-p2)(A1-λA2)+2Fs]μ+G

(5)

式中：p1为高压侧压力；p2为低压侧压力；A1为高压侧环形端面面积；A2为低压侧环形端面面积；λ为气膜反压系数，取λ=0.7。

2.2 动态间隙计算

浮环上浮力受气膜厚度影响，故提取上浮力之前需先确定密封组件的动态间隙。温度及转速的变化均会对动态间隙造成影响，以某航空发动机浮环密封装置为参考，采用Ansys-Workbench静力学分析模块，分别建立浮环模型与跑道模型，根据实际工况施加过盈载荷、温度载荷、转速载荷等边界条件进行有限元分析。模型中的材料参数和结构参数分别如表1、表2所示。

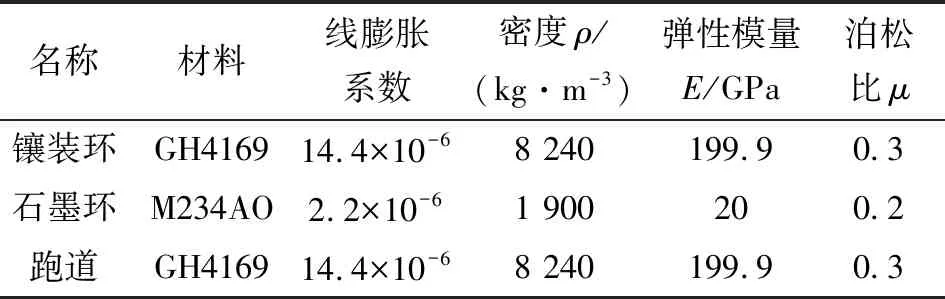
表1 模型中的材料参数

表2 模型中的结构参数 单位:mm

计算完成后提取跑道外壁径向变形计算结果如图2所示，浮环内壁径向变形结果如图3所示。

图2 跑道径向变形Fig 2 Radial deformation of the runway

图3 浮环径向变形Fig 3 Radial deformation of the floating ring

从图2和图3可以看出,浮环与跑道变形值在轴向上变化不大，故可取上下限的平均值以便后续气膜模型的建立。则平均气膜膜厚为

H=δR+δR1-δR2

(6)

式中:H为浮环平均动态半径间隙；δR为浮环初始半径间隙；δR1为浮环工作状态平均半径变形量；δR2为跑道工作状态平均半径变形量。

2.3 气膜浮环有限元模拟分析

浮环开车前的状态如图4所示，建立气膜模型前需先确定偏心距e0。

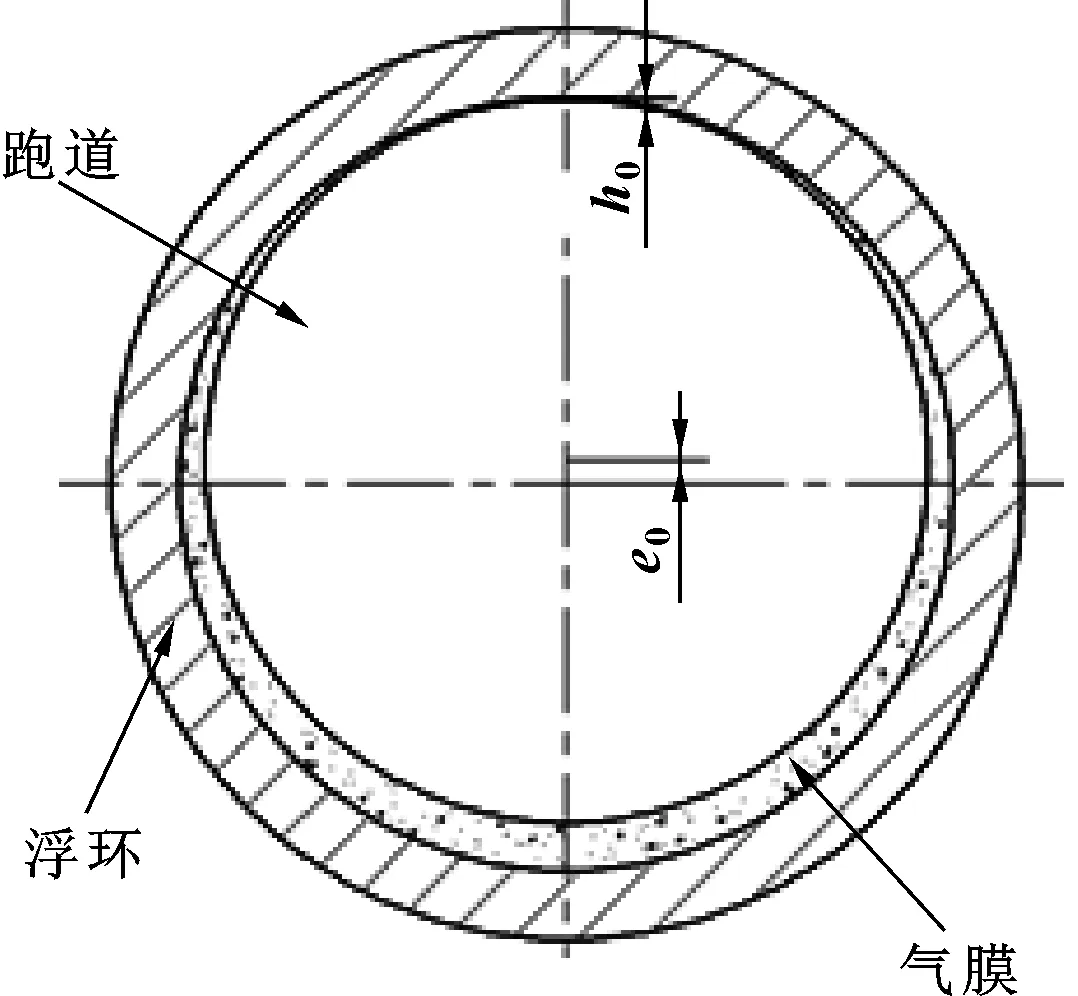
图4 浮环开车前状态示意Fig 4 Schematic of the floating ring state before operating

图4中h0称为接触气膜厚度，当最小气膜厚度hmin大于或等于接触气膜厚度，密封面分开，浮环开始上浮，接触气膜厚度[13-16]定义为

(7)

式中:Ra1为跑道外表面粗糙度;Ra2为石墨环内壁表面粗糙度。

则初始偏心距：

e0=H-h0=H-0.003 35

采用Workbench中的Fluent模块建立偏心气膜分析模型。分别命名边界：air-in，air-out，mobile-face，fixed-face。固定fixed-face并在mobile-face施加指定转速，在air-in端面加载高压侧压力，在air-out端面施加高压侧压力。气膜模型及对应的操作参数分别如图5和表3所示。

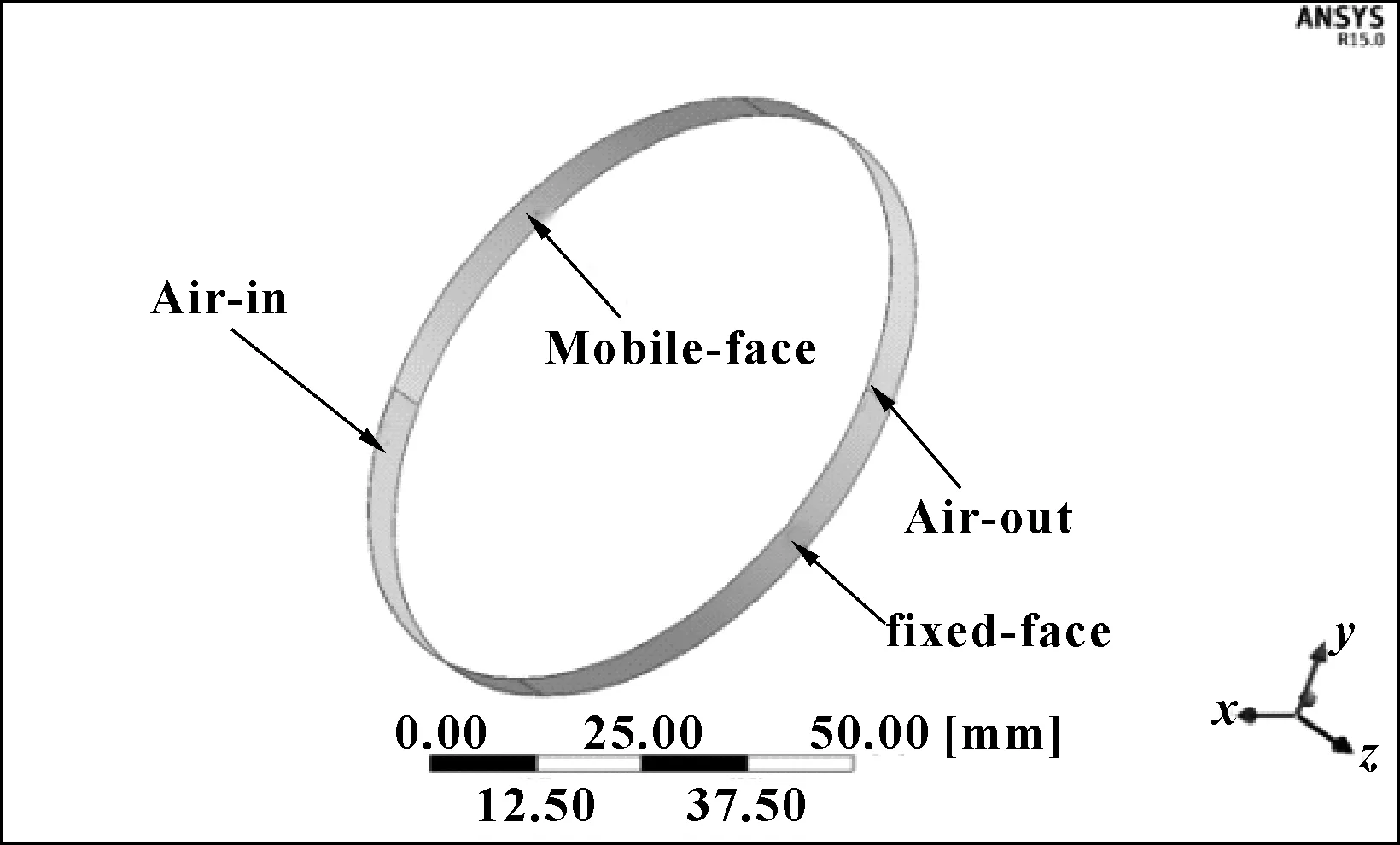
图5 气膜有限元模型Fig 5 gas film finite element model

表3 气膜模型中的操作参数Table 3 Operating parameters in the gas film model

计算完成后提取的气膜压力云图如图6所示，可知气膜压力沿轴向并不是均匀分布的，沿旋转方向在点A(膜厚最小处)前端形成一个高压区，高压区的压力大于入口压力。在点A后端形成一个低压区，低压区的压力小于出口压力。分析是由于点A处膜厚较小，气体在通过点A时“憋压”，导致点A前端压力较高。同时气体来不及通过点A，故在点A后端压力较低。

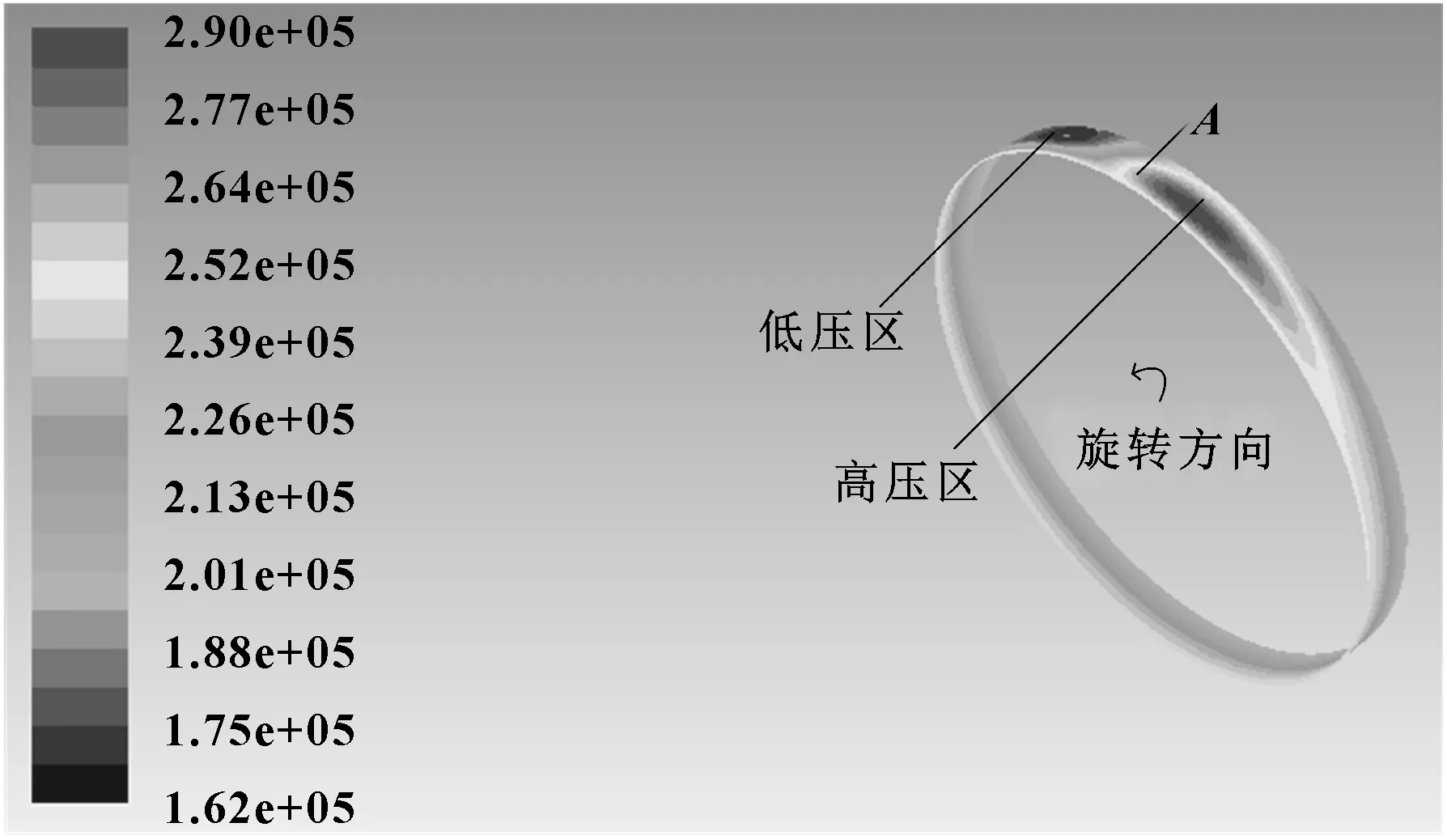
图6 气膜压力云图Fig 6 Gas film pressure cloud map

设置不同的转速，分别提取对应计算结果下y方向的上浮力。当上浮力略大于上浮阻力时，对应的转速即为理论上的浮环临界上浮转速。总结前文，可得到气膜浮环上浮转速的计算流程如图7所示。

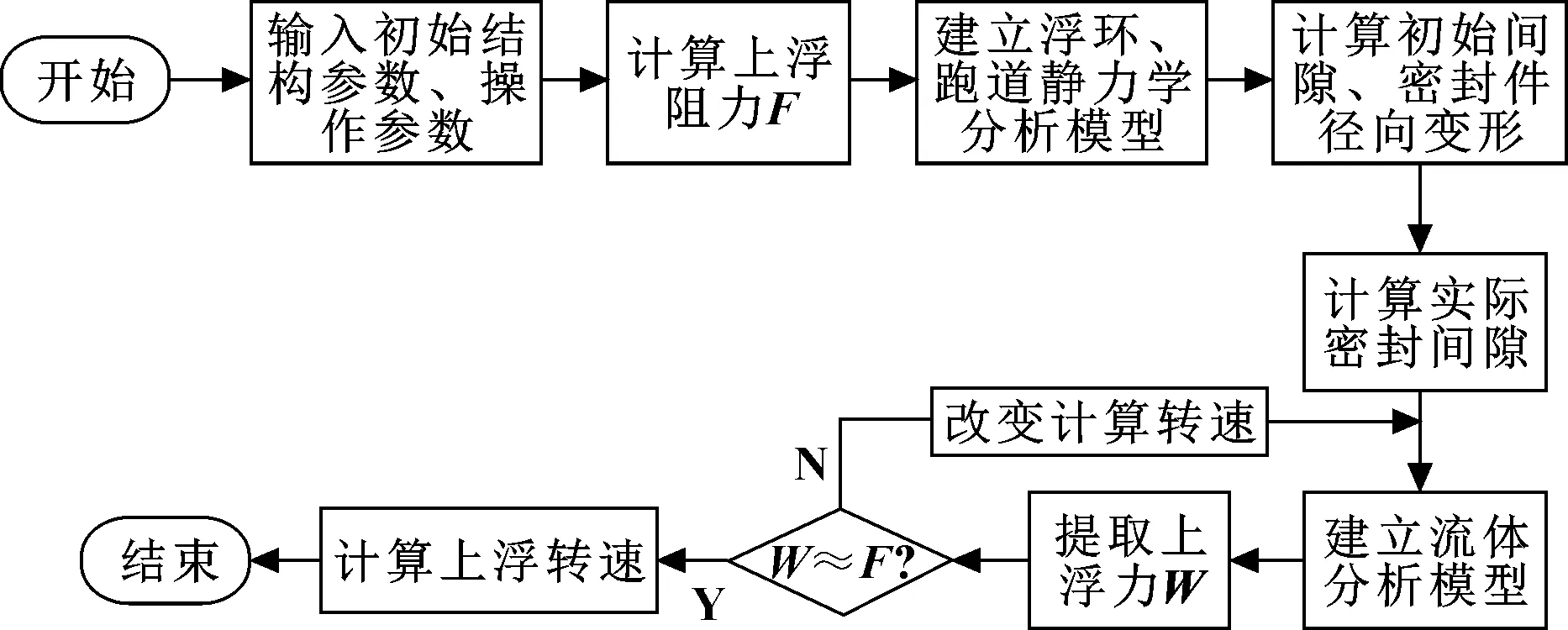
图7 上浮转速计算流程Fig 7 Flow of floating speed calculation

同时若固定转速为浮环工作状态的转速，改变模型的偏心率(偏心距与动态间隙的比值)，当上浮力等于上浮阻力时，对应的偏心率即为浮环工作状态的偏心率，提取得到的泄漏率为工作状态的泄漏率。分别设置不同的偏心率计算提取对应的泄漏率和上浮力，得到偏心率-上浮力-泄漏率关系如图8所示。

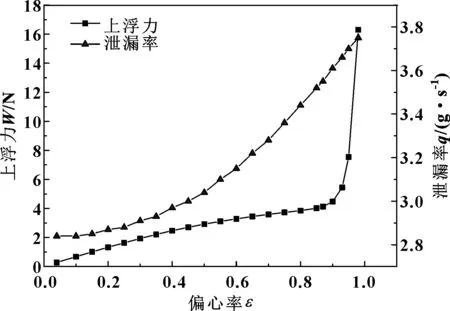
图8 上浮力和泄漏率随偏心率的变化Fig 8 Variation of buoyancy and leakage with eccentricity

从图8可以看出，当偏心率小于0.9，气膜浮环的上浮力与偏心率成低斜率的线性关系；而当偏心率大于0.9时，上浮力发生畸变，仅0.05的偏心率变化导致上浮力增加了10 N。浮环的泄漏率随偏心率的增加而增加且呈近似二次关系，这与液膜浮环的压差流动[17]类似，原因是浮环两侧压差较小，节流通道里的空气可近似看为不可压缩流体。同时可知偏心率较小的浮环泄漏量较小，密封性能更佳。

3 上浮转速影响因素分析

发动机开车时需根据实际情况选择操作条件的 施加顺序，一般来说分2种情况：一是先增压至工作压力再增速；二是先增速到工作转速再增压，2种情况下的临界上浮转速并不相同。根据图7所示的上浮转速计算流程，分别探究密封系统在2种情况下各参数对上浮转速的影响并进行对比分析。

3.1 节流长度

节流长度即石墨环内表面的宽度。保持轴宽比(镶装环与石墨环宽度比值)不变，其他参数按表1—3，改变节流长度，建立密封组件模型得到动态间隙并建立气膜模型,计算得到的节流长度与上浮转速关系如图9所示。

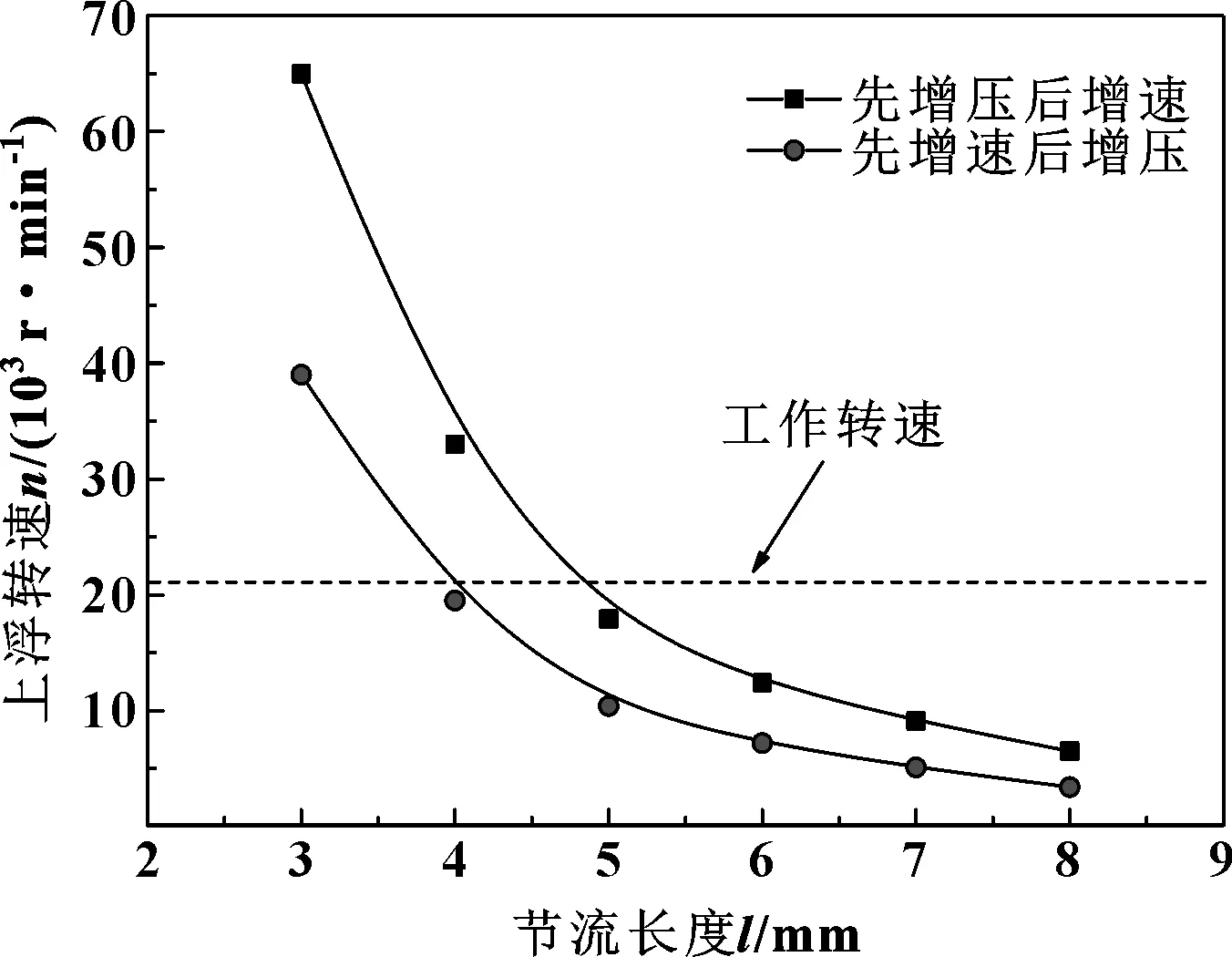
图9 上浮转速随节流长度的变化Fig 9 Variation of floating speed with throttle length

从图9可以看出，2种情况下上浮转速随节流长度变化的趋势相同，且先增速后增压时的浮环上浮转速较低，上浮性能较好。当节流长度较小时上浮转速变化比较灵敏，节流长度较大上浮转速变化趋于平缓。另外节流长度对上浮转速的影响非常大，当节流长度为3 mm时上浮转速甚至达到了65 000 r/min，远远超过了此航空发动机的工作转速20 900 r/min(图中虚线)，此时的浮环是不能上浮的。而当节流长度较大时浮环的上浮转速很低，上浮性能较好。但太大的节流长度会使密封结构占据更多的轴向空间。因此在实际设计气膜浮环时需充分考虑节流长度对上浮转速的影响。建议节流长度取5～7 mm为宜。

3.2 载荷系数

载荷系数K既是几何参数也是力学参数，在这里其为高压侧与低压侧端面面积之比，即K=A1/A2。取载荷系数1.5～6，探讨载荷系数与上浮转速关系，如图10所示。

由图10可知先增速后增压时浮环上浮转速较低，上浮性能较好。先增速后增压时上浮转速几乎不变，这是由于浮环两侧没有压差，上浮阻力与上浮力并不会受A2的变化影响，故上浮转速稳定不变。先增压后增速时上浮转速随载荷系数的增大而增大且斜率逐渐减小，这是由于当载荷系数增大时A2减小，由上浮阻力计算式(5)可知上浮阻力随之增大，故上浮转速增大。2种情况下载荷系数从极小取到极大的过程，浮环总能够上浮，工程设计时建议取载荷系数1.5～3。

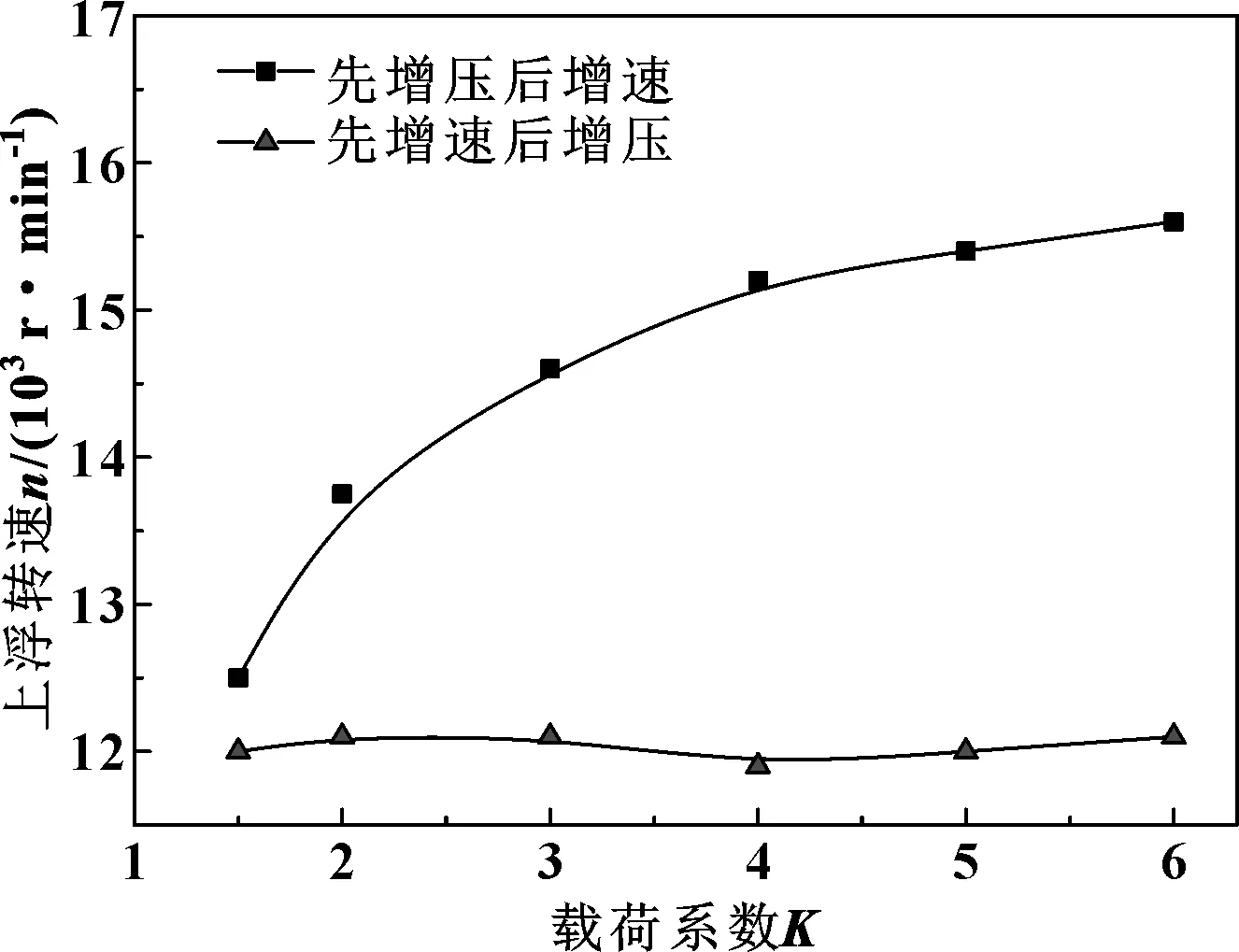
图10 上浮转速随载荷系数的变化Fig 10 Variation of floating speed with load factor

3.3 径向间隙

考虑到实际浮环的泄漏要求，根据经验使浮环的工作间隙取到0.02～0.07 mm，建立模型并分析计算，得到的径向间隙与上浮转速关系如图11所示。

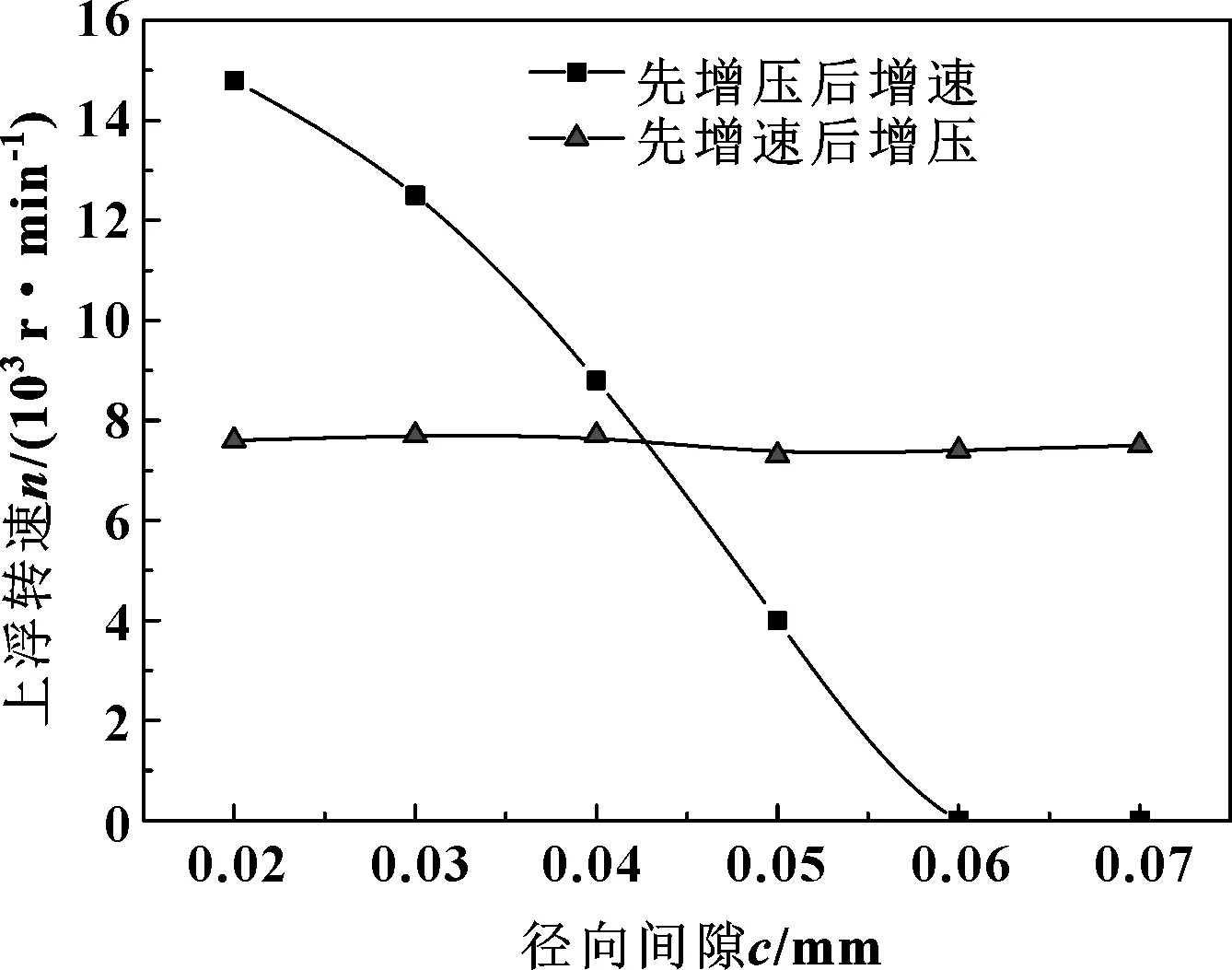
图11 上浮转速随径向间隙的变化Fig 11 Variation of floating speed with radial clearance

由图11可知，间隙较大时先增压后增速时浮环上浮性能较好，间隙较小时先增速后增压时浮环上浮性能较好。先增压后增速时上浮转速随着径向间隙的增大逐渐减小，且当径向间隙达到0.06时上浮转速为0，此时仅靠压差的作用浮环就能浮起。这是由于环向间隙的变化导致气体流沿环向并不相同，即使在静止状态流体运动产生的上浮力也足以克服上浮阻力使浮环上浮。先增速后增压时浮环两侧压差为0，气体流动时没有轴向的分速度故上浮转速较为稳定，径向间隙的变化并不会对上浮转速产生大的影响。

3.4 波簧弹力

保持其他条件不变，取波簧弹力4～14 N,探讨波簧弹力与上浮转速关系，如图12所示。可知在一定范围内2种情况下的上浮转速均随波簧弹力的增大线性增大，浮环在整个波簧弹力取值范围内均可上浮。

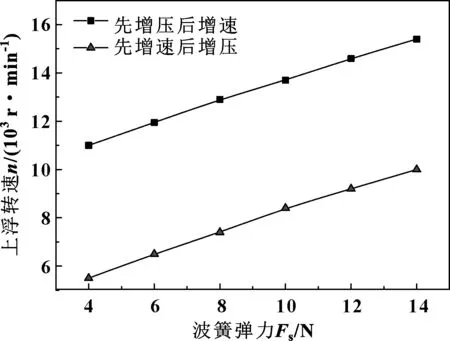
图12 上浮转速随波簧弹力的变化Fig 12 Variation of floating speed with wave spring elastic

3.5 工作温度

温度的变化会影响动态间隙以及空气黏度从而影响上浮转速，改变密封组件的操作温度得到相应的动态间隙，建立气膜模型施加边界条件，计算得到的工作温度与上浮转速关系如图13所示。

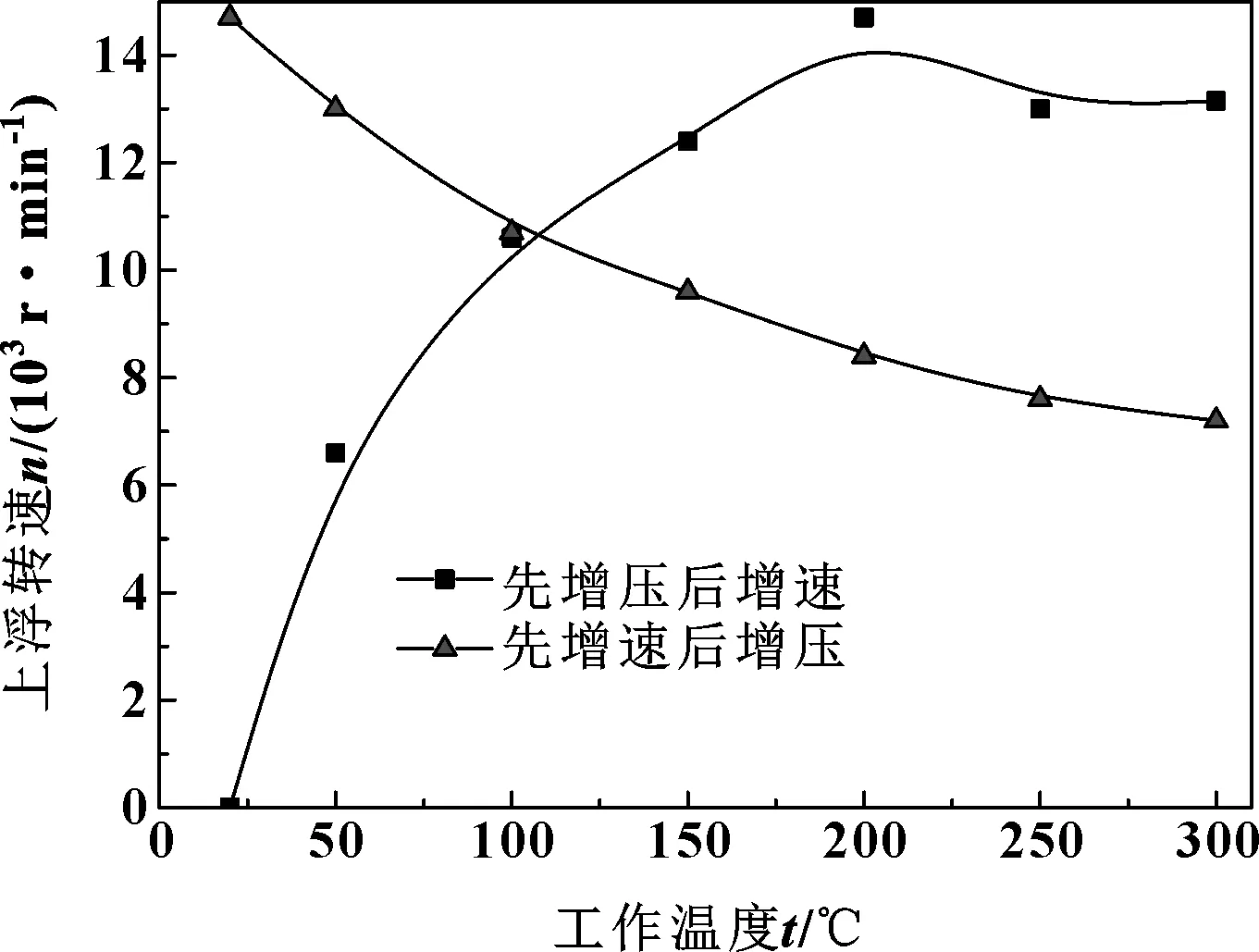
图13 上浮转速随工作温度的变化Fig 13 Variation of floating speed with operating temperature

由图13分析可知，先增压后增速时上浮转速同时受间隙变化和空气黏度变化的影响，温度从20 ℃增加至200 ℃上浮转速从0增加到了14 000 r/min，这是由于当温度升高时，动态间隙减小导致上浮转速增大。而当温度大于200 ℃上浮转速反而有减小趋势，这是由于当温度升高到一定程度，空气黏度变化产生的负作用超过了间隙变化产生的正作用。先增速后增压时，间隙的变化对上浮转速不再产生影响(如图11所示)，而空气黏度的降低导致了上浮转速的降低。

3.6 高低压侧压差

压力的变化会影响侧壁的摩擦力与流体的轴向流速，取高低压侧压差0～0.12 MPa建立模型并计算，得到压差与上浮转速关系，如图14所示。可知随浮环两侧上浮转速与压差正相关且在取值范围内浮环均能上浮。

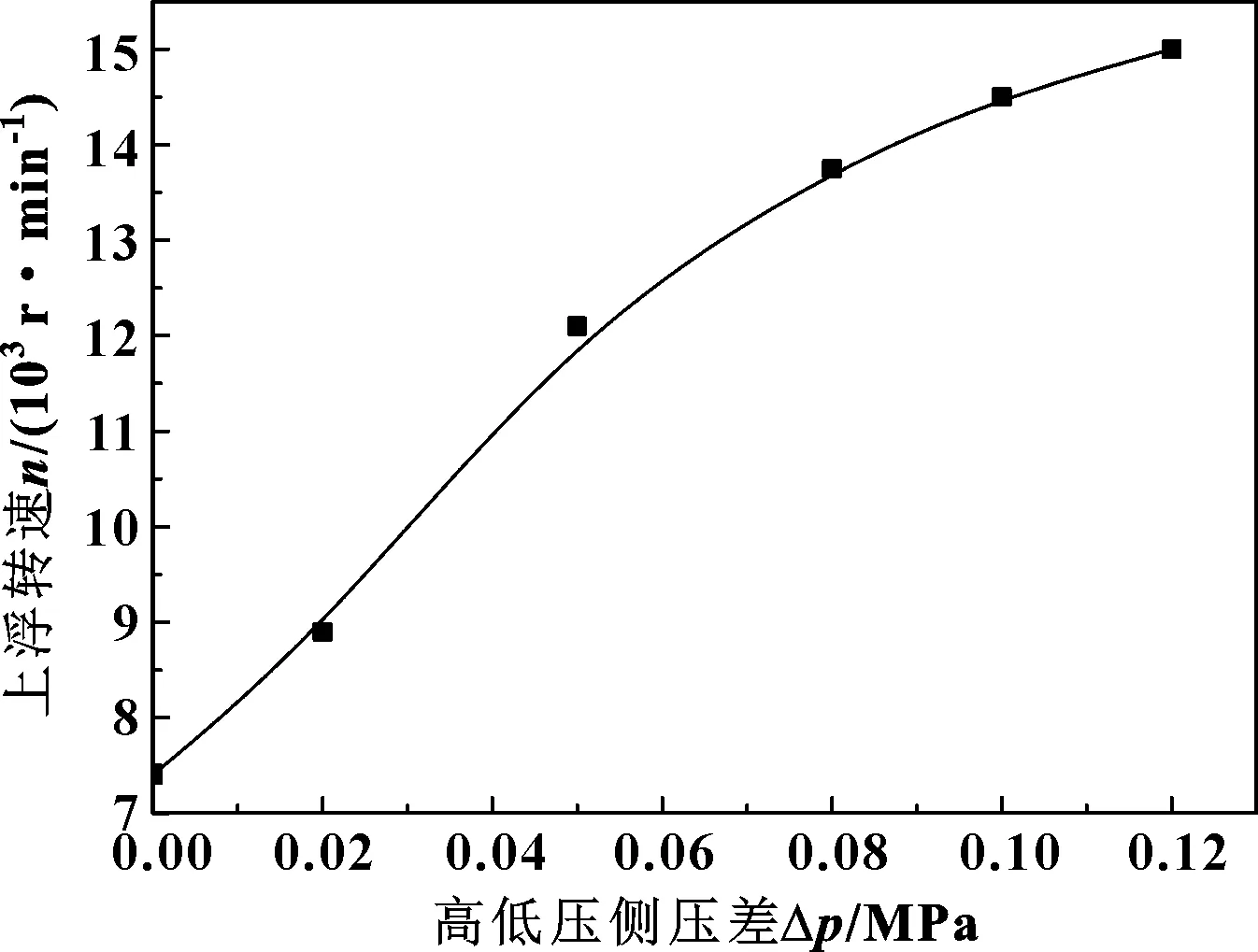
图14 上浮转速随压差的变化Fig 14 Variation of floating speed with pressure difference

4 气膜浮环上浮转速试验验证

为验证有限元分析的正确性，开发了浮环密封上浮转速试验装置。图15(a)所示为试验主体装置，图15(b)所示为浮环密封组件。试验前通过位移传感器探测口推动浮环使其贴合在跑道上，再安装位移传感器并开车;逐渐增加转速,当传感器检测到位移变量时，此时的转速即为上浮转速。

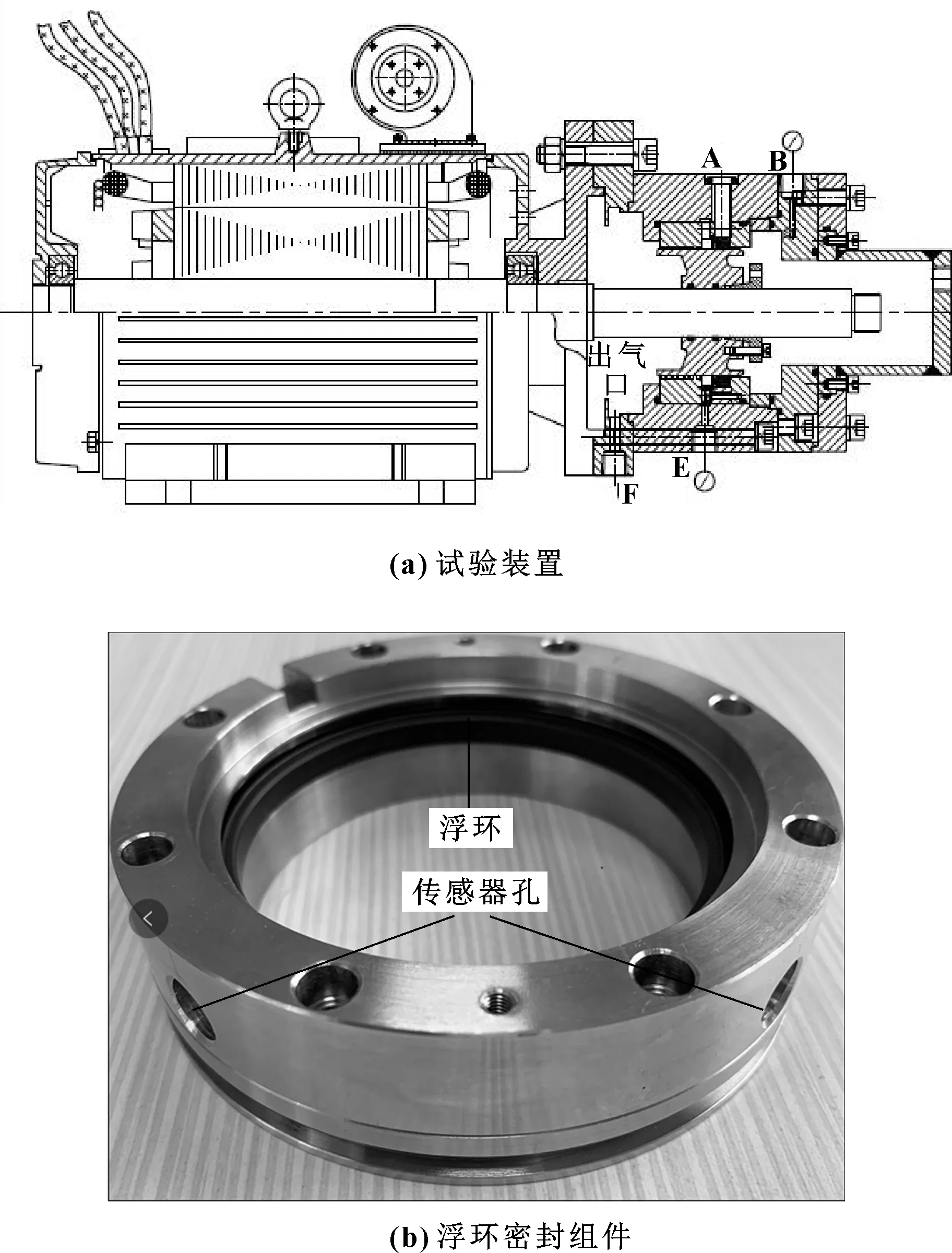
图15 试验装置及浮环密封组件Fig 15 Test device(a)and floating ring seal assembly(b)

验证试验采用先增压后增速的方式，浮环初始半径间隙实测值为0.042 mm。为方便试验,出口压力取常压，温度取常温，得到不同压差下上浮转速理论值与试验值对比如图16所示。取出口压力为常压，压差0.05 MPa，得到不同温度下上浮转速理论值与试验值对比如图17所示。

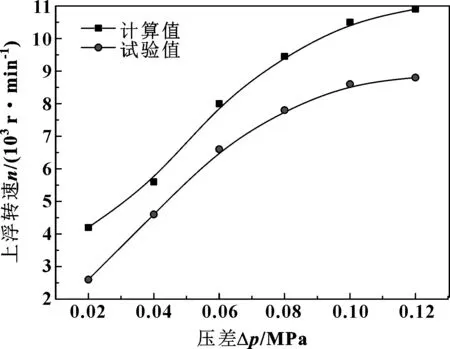
图16 不同压差下上浮转速计算值和试验值对比Fig 16 Comparison of calculated and experimental values of floating speed under different pressure differences

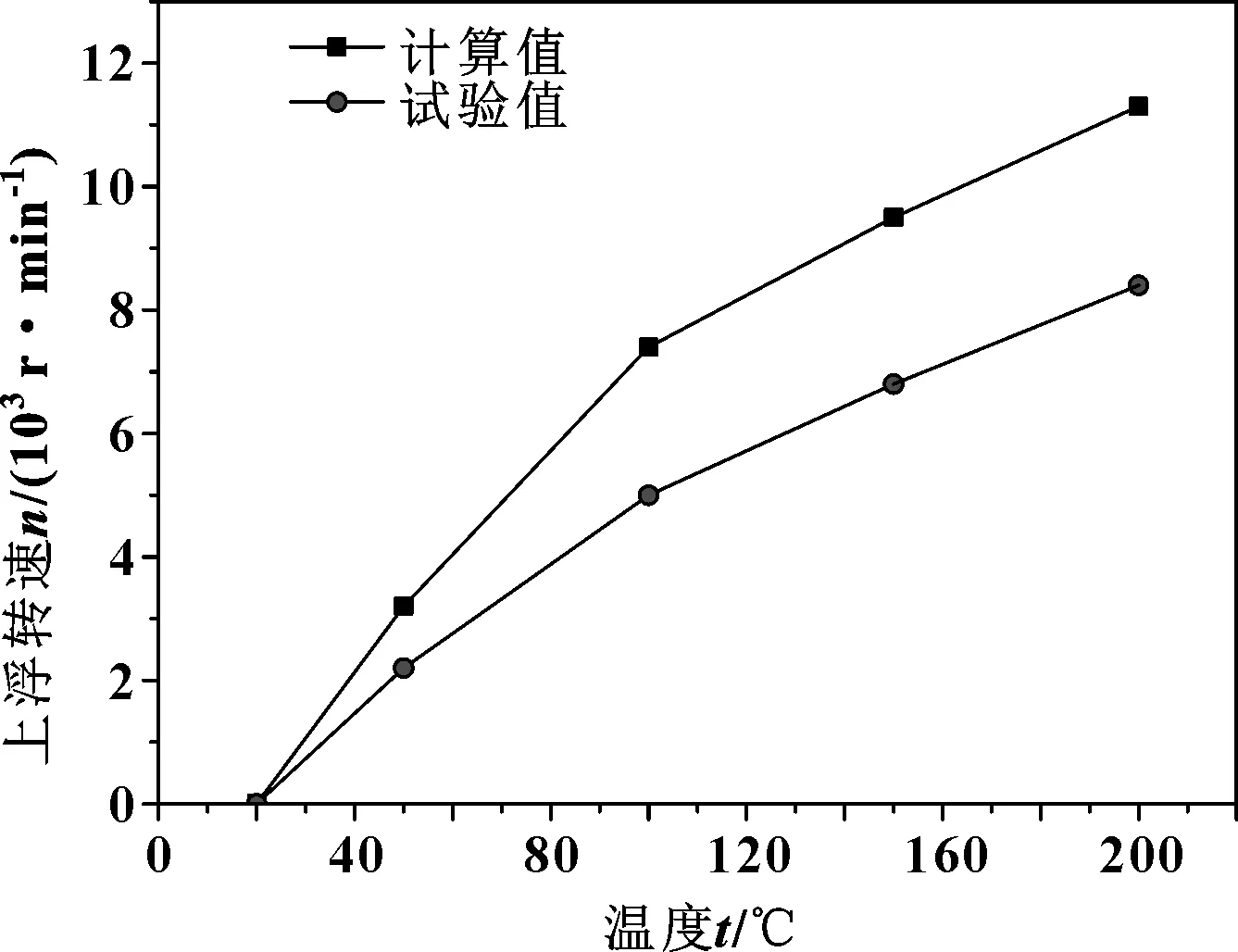
图17 不同温度下上浮转速计算值和试验值对比Fig 17 Comparison of calculated and experimental values of floating speed under different temperature

由图16、图17可知，上浮转速有限元模拟值与计算值变化趋势相同。由于试验过程存在不可控误差，故模拟值与试验值大小存在一定差异，但在可接受范围内，故可认为文中所进行的有限元分析结果是可靠的。

5 结论

(1)气膜浮环的上浮力随偏心率增大而增大且存在一个畸变过程，泄漏率与偏心率正相关且低压差下呈近似二次关系，偏心率较小的浮环密封性能更佳。

(2)节流长度对上浮转速影响极大，节流过小将导致浮环不能上浮，工程设计时推荐节流长度5～7 mm；载荷系数对上浮转速的影响稍小，工程设计时推荐取1.5～3。

(3)不同的操作方式下各密封参数对气膜浮环上浮性能的影响呈现很大的差异性。先增速后增压时上浮转速与载荷系数、波簧弹力、压差正相关，与节流长度和径向间隙负相关；先增压后增速时上浮转速与波簧弹力正相关，与节流长度、工作温度负相关，与载荷系数、径向间隙几乎不相关。综合来说先增速后增压时上浮性能较好，有条件时开车前应先进行上浮性能的分析再选择操作条件施加的顺序。