干气密封滑动密封端面高频微幅摩擦振动研究*
2021-01-20孙宝财丁雪兴严如奇陈金林
孙宝财 丁雪兴 严如奇 陈金林
(1.兰州理工大学石油化工学院 甘肃兰州 730050;2.甘肃省特种设备检验检测研究院 甘肃兰州 730050)
理论上讲,干气密封只有在启动、停止阶段两端面才会出现接触摩擦[1]。但是,在实际工程应用过程中,由于加工制造、装配误差和工作环境的影响,干气密封端面在正常的运行阶段也会发生接触摩擦的情况[2],此时,干气密封端面将处于无任何润滑的干摩擦状态之下。物体结构表面一般都具有一定的粗糙度,故动、静环端面相互接触时,真正的接触只发生在个别粗糙峰(即微凸体)的顶部,接触点呈离散分布状态,而大部分区域都是有间隙的[3]。这就意味着两密封端面处于干摩擦状态时,将会发生微凸体间的随机接触与碰撞,进而引起摩擦振动。与此同时,伴随着密封端面的划伤和磨损、噪声、温升等现象,最终,整个密封系统将会在这些因素的累积作用下失稳,直至失效。
目前,干气密封的摩擦、磨损等研究逐步引起了人们的关注。HUANG等[4-5]用声发射技术对干气密封启动、停止阶段,以及运行过程中的碰摩引起的摩擦进行了测试分析,并指出用声发射技术能够有效地检测密封端面的碰摩。丁雪兴等[1-2]通过对螺旋槽干气密封环进行摩擦性能试验,分析了不同工况下的密封环磨损量、摩擦因数之间的变化规律。除此之外,关于干气密封摩擦相关的研究还鲜见报道。摩擦振动是机械运动摩擦副在摩擦磨损过程中产生的普遍现象,蕴含着许多反映系统摩擦学特征和摩擦状态的信息[6-7]。因此,对干气密封端面进行干摩擦状态下的摩擦振动研究具有至关重要的意义。
1931年,DEN HARTON[8]最早开始了摩擦振动的分析研究,通过建立微分方程来描述单自由度系统的黏滑运动,提出了一种近似且摩擦因数恒定的理想干摩擦模型。PANOVKO和GUBANOVA[9]运用数值方法对摩擦振动里面的自激振动进行了研究,并指出自激振动仅仅发生在一定速度范围之内。之后,YEH[10]将HARTOG的精确解法推广至含有一个干摩擦环节的两自由度系统。FEENY和MOON[11]研究和探讨了非光滑的库仑摩擦振子的动力学行为,并给出停滞范围的解析表达式和图解。ELMER[12]对无阻尼和不同摩擦函数时的质量块带的黏滑和纯滑动振动进行了研究,提出了黏滑和纯滑动振动之间转换的表达式。DANKOWICZ和NORDMARK[13]通过变化正压力来确定摩擦振动解的产生和分岔。THOMSEN和FIDLIN[14]给出了一个非线性摩擦模型的黏滑振动的幅值、频率的近似表达式,之后,又用摄动法分析了滑动阶段和黏滑阶段。丁旺才等[15]对含干摩擦振动系统的非线性动力学进行了分析,给出了判定系统滑动状态与黏着状态分界点的理论方法,分析了由干摩擦引起的黏滑振动。MASSI等[16]从摩擦界面出发研究摩擦表层的变形、接触表面的粗糙度等与摩擦噪声的内在联系,认为由于表面形貌使得摩擦力存在动态分量,从而激励结构发生共振与尖叫。田永伟和杨建刚[17]针对摩擦转子系统动力特性建立一种耦合分析模型,对旋转机械动静碰摩耦合振动进行了分析。GDANIEC等[18]采用LuCre摩擦模型对单自由度摩擦振子进行了研究,发现速度和摩擦因数会诱发振动中的分岔和混沌现象。张海涛和丁千[19]利用同伦方法研究了纯滑动和黏滞-滑动形式的干摩擦自激振动。GOLA和LIU[20]在切向方向采用不考虑微观滑移的摩擦模型,在法向方向用线性弹簧模拟法向载荷的变化,建立了模拟发动机叶片阻尼器运动的七自由度模型,并和实验结果进行了对比,验证了模型的有效性。李小彭等[21]建立了含有Stribeck摩擦模型的具有代表性的质量-弹簧-带摩擦自激振动系统非线性动力学模型,对其分岔特性及其控制进行了研究。之后,李小彭等[22]、潘五九等[23]又对车辆制动盘制动工况进行抽象综合,给出了两自由度系统的物理和数学模型,对结合面微观形貌对由摩擦和系统结构双重引起的模态耦合系统不稳定性进行了分析研究。
上述研究均是在干摩擦状态下对黏滑和纯滑动振动进行研究,并从一个自由度扩展到两自由度系统,所涉及的摩擦模型也逐步从静态摩擦模型向动态摩擦模型过渡。然而,与之类似的干气密封端面间的纯滑动摩擦振动研究还未见报道。本文作者通过对密封端面在干摩擦状态下进行受力分析,基于分形理论建立了干气密封端面间考虑微观形貌与接触特性对宏观系统影响的两自由度摩擦振动系统模型,并对其摩擦振动规律以及影响因素进行了数值分析与讨论,为深入研究干气密封摩擦振动提供了一定基础。
1 密封端面物理与数学摩擦振动模型
1.1 密封端面振动系统物理模型
干气密封动环与静环在干摩擦状态时形成的摩擦副如图1所示。滑动粗糙表面(动环)在法向载荷p作用下沿着固定粗糙表面(静环)滑动。对静环来说滑动摩擦产生切向力Qx,在整个接触面内平行于x轴,并与动环滑动方向相同。两密封面在滑动过程中,在法向载荷p与滑动摩擦产生的切向力Qx共同作用下,在整个接触面内,部分微凸体处于塑性接触状态,其在接触过程中耗散接触力所做的功,表现为阻尼作用;部分微凸体处于弹性接触状态,其在接触过程中发生弹性变形而存储接触力所做的功,表现为刚度作用。此外,在滑动过程中,表面微凸体的起伏将会引起动环在法向(z轴方向)的振动,因此需要考虑微观形貌对摩擦振动的影响。
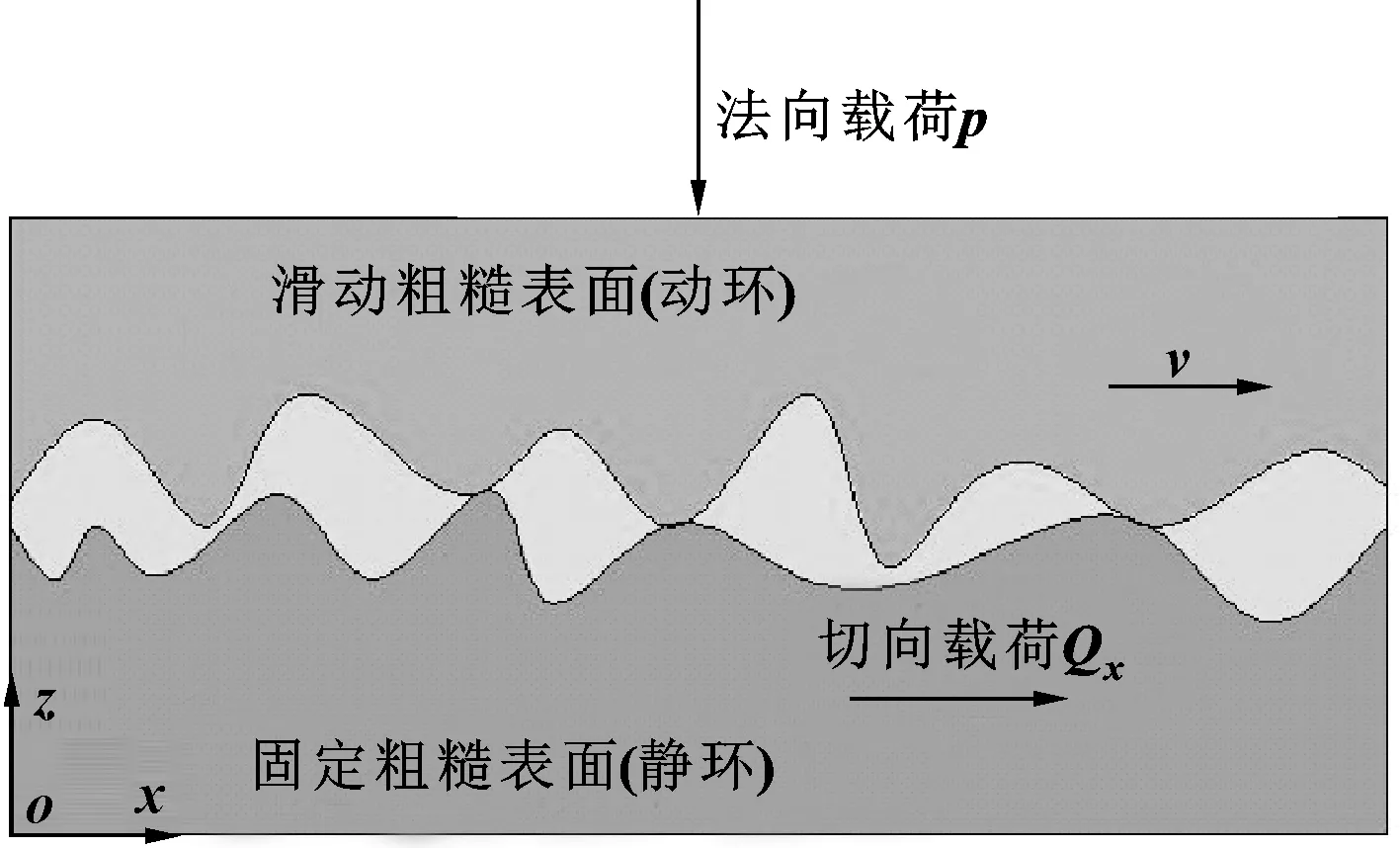
图1 滑动摩擦下动环与静环之间的接触Fig 1 Contact between moving ring and stationary ring under sliding friction
为了研究干气密封在干摩擦状态下的摩擦振动,并简化该问题的复杂度,做出如下假设:
(1)将干气密封硬质环与软质环的接触简化为滑动刚性理想光滑平面与固定粗糙表面的接触;
(2)为刻画在滑动过程中微凸体起伏引起动环在法向(z轴方向)的振动,假定静环粗糙表面按分形参数构成的余弦规律变化;
(3)将摩擦振动分为正交的2个方向:垂直于密封端面的法向(z轴方向),平行于密封端面的切向(x轴方向);
(4)接触刚度分为法向接触刚度与切向接触刚度;
(5)接触阻尼分为法向接触阻尼与切向接触阻尼;
(6)以动环为振动研究对象。
基于以上分析,抽象并建立了干气密封在干摩擦状态下考虑微观接触特性对宏观系统影响的两自由度摩擦振动系统模型,如图2所示。
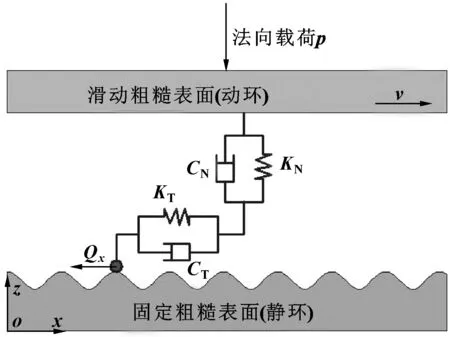
图2 干气密封两自由度摩擦振动系统模型Fig 2 Model of dry gas seal two degrees of freedom friction vibration system
图2中,KN、KT表示动环与静环滑动摩擦界面之间的法向接触刚度与切向接触刚度(N/m);CN、CT表示摩擦界面之间的法向接触阻尼与切向接触阻尼(N·s/m);p代表法向载荷(N),Qx为滑动摩擦产生的切向力(N),Qx=fp,其中f为摩擦因数。
1.2 密封端面法向位移激励建模
两密封面在滑动过程中,表面微凸体的起伏将会引起动环在法向(z轴方向)的振动,即微凸体起伏引起的法向位移成为激励。因此,需要构建密封端面法向位移激励的表达式。
具有分形特征的粗糙表面的轮廓曲线可用W-M函数来描述[24],其数学表达式如下。
(1)
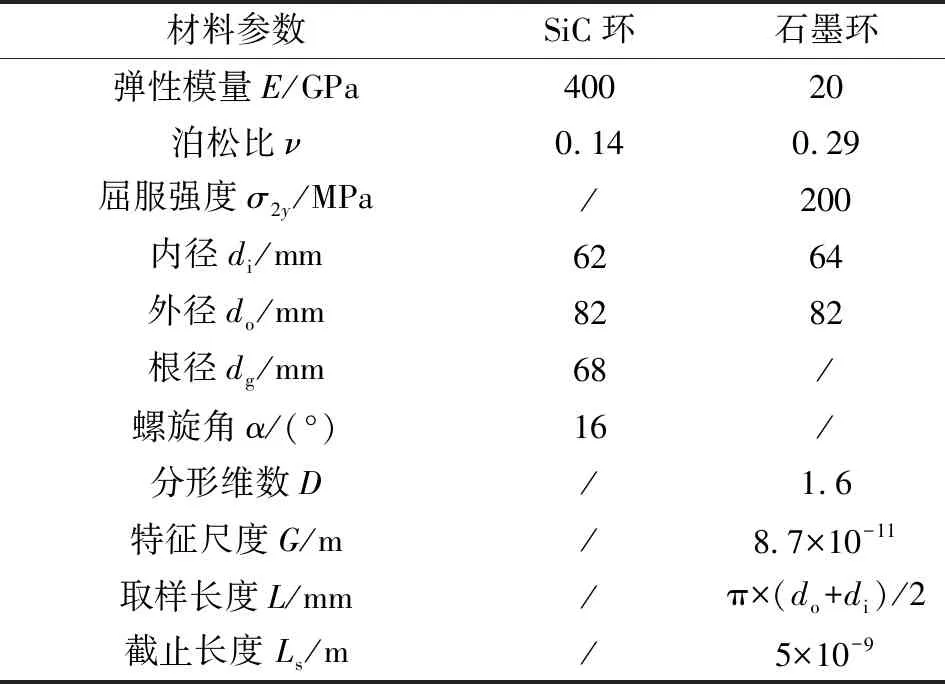
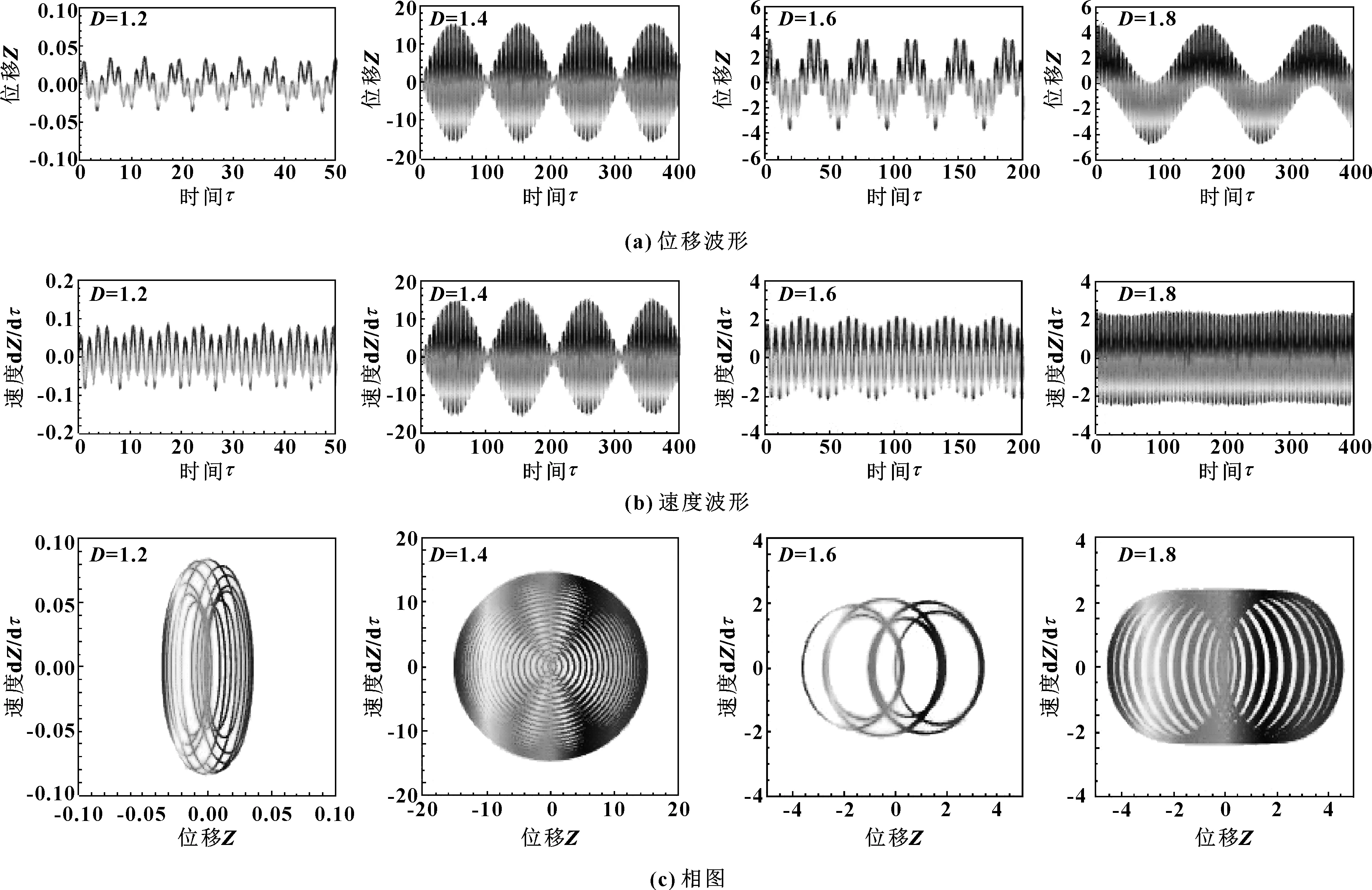
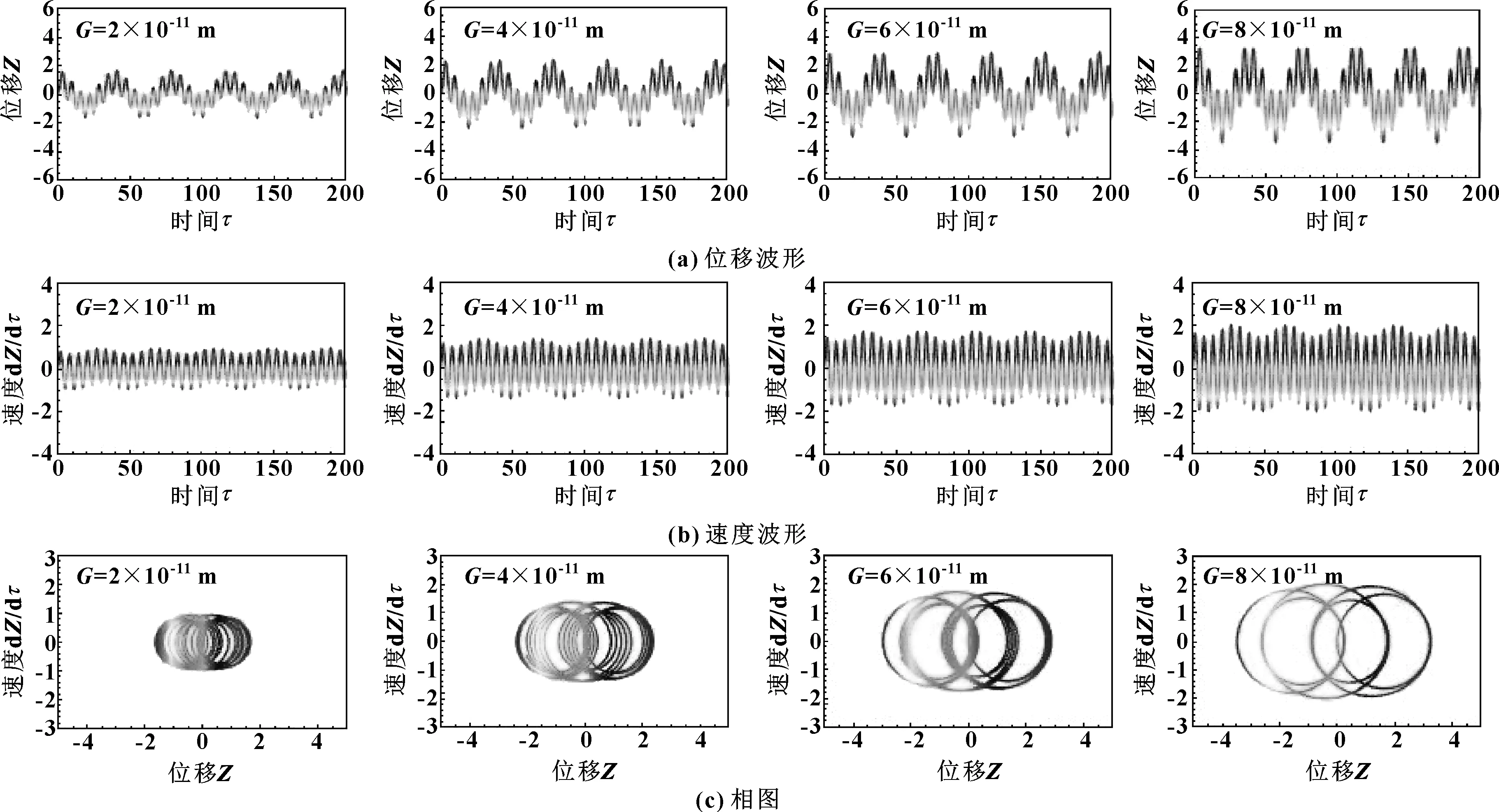
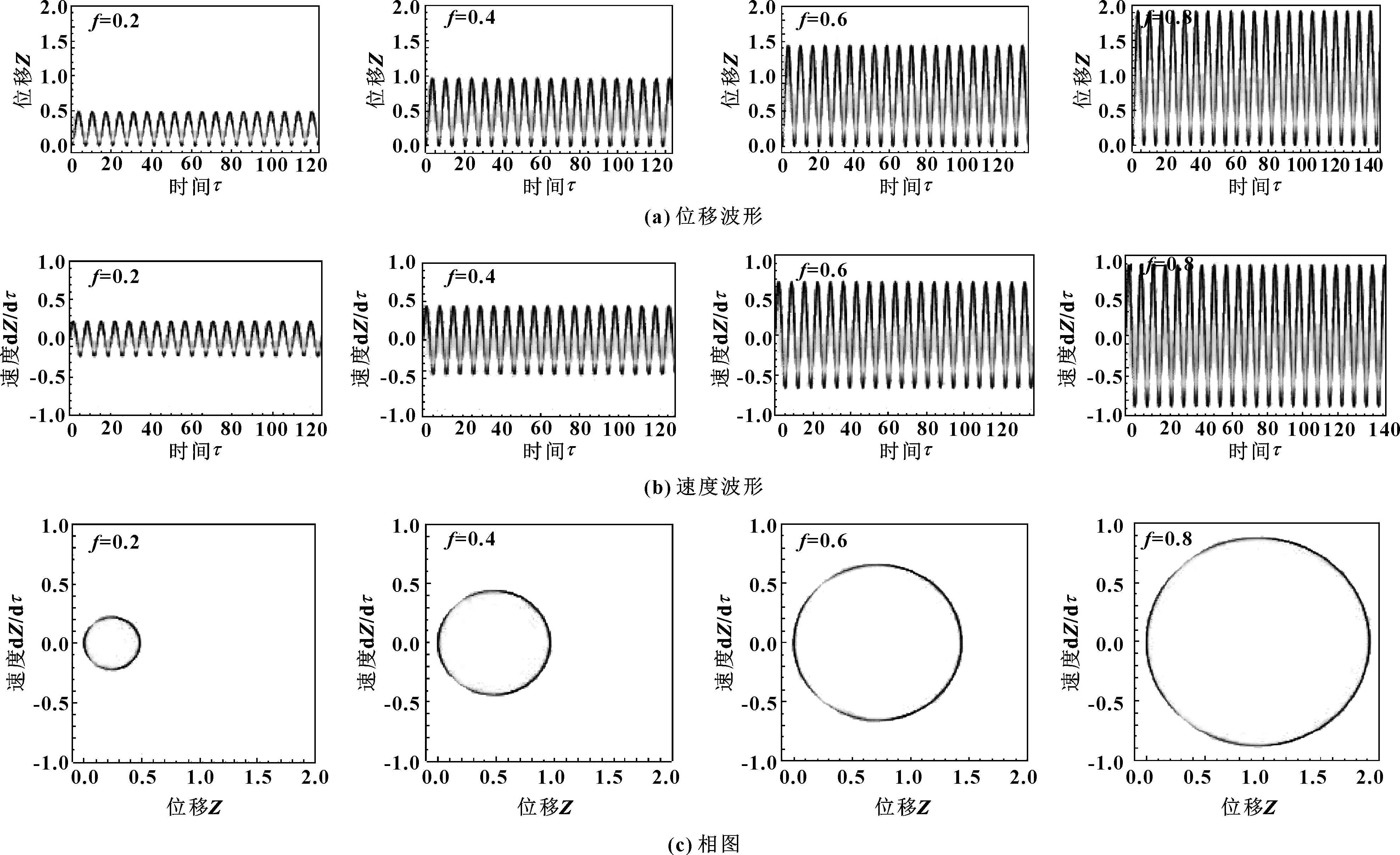
式中:D为分形维数(1 由式(1)可知,变形前单个微凸体可以定义[3]为 (2) 式中:lb为基底长度(m)。 通过以上简化与假设以及式(2),微凸体起伏引起的法向位移激励可以定义为(文后所出现的z(x),均表示法向方向的激励) z(x)=Zgcos(Ωt) (t≥0) (3) 基于前文构建的干气密封端面振动系统物理模型与法向位移激励,建立干气密封在干摩擦状态下考虑微观形貌与接触特性对宏观系统影响的两自由度摩擦振动系统数学模型。对图2所示系统,其动力学方程为 (4) 为便于分析该动力系统,将方程(4)化为量纲一化形式: (5) 该动力系统方程,包含有接触阻尼、接触刚度以及激励,其更接近实际情况。当前,在文中暂只考虑无阻尼下系统的稳态解。则方程(5)在不考虑阻尼的情况下为 (6) 对于式μk,t中所涉及的切向接触刚度与法向接触刚度,分别引用文献[25-26]中公式,具体如下: (7a) (7b) (7c) (8a) (8b) (8c) 通过对式(7)与式(8)进行分析不难发现,切向接触刚度与法向接触刚度的比值为一定值,且与材料本身有关。 (9a) (9b) (9c) 文中将硬质环(动环SiC)简化为刚性理想光滑平面,软质环(静环碳石墨)简化为粗糙表面进行摩擦振动分析。动环SiC、静环碳石墨相关参数引自参考文献[26] ,具体见表1。由于静环自身几何结构因素,在表1中个别参数将不予考虑。 采用控制变量法分析不同分形维数对振动系统的影响。将表1数据代入式(6),并取载荷3 000 N、摩擦因数f=0.15、转速3 000 r/min,可得不同分形维数取值下振动系统的变化规律。但从式(6)可以看出,μk,t在材料一定时不受分形维数、特征尺度、转速的影响,所以在材料、工况一定,且在不考虑阻尼的情况下,系统切向方向的振动规律只与摩擦因数有关,将不受分形维数、特征尺度、转速的影响,而法向方向的振动规律则均与上述因素有关。因此,下面将分别就法向方向与切向方向的振动规律进行分析讨论。 表1 算例计算参数 当系统初始参数一定,分形维数D分别取1.2、1.4、1.6、1.8时,系统法向振动位移波形、速度波形、相图如图3所示。 图3 不同分形维数下的法向振动规律Fig 3 Normal vibration law under different fractal dimensions (a)displacement waveform;(b)speed waveform;(c)phase diagram 从图3可以得出: (1)随着分形维数D的增大,法向振动位移与速度均先增大后减小,然后略有提高。但值得注意的是,在分形维数D=1.4时出现拍振,从这一现象可以推测必然存在某一分形维数使法向振动出现共振。分形维数D分别取1.2、1.4、1.6、1.8时,可得相应的Ω0分别为3.71、0.938、0.167、0.037。由此可以判定,出现共振的分形维数在1.3左右。为避免工程实际应用中密封面出现共振现象,密封面分形维数应大于1.4。 (2)当分形维数D>1.4时,法向振动呈现出一种高频微幅的稳定振动现象(如,分形维数D=1.6时,法向固有频率ωN=2.387×106(约380 kHz),法向振动位移幅值Zg=2.206×10-8m)。从位移波形图中可以看出,这种高频微幅振动在较小的范围内变动,且以周期重复出现性质相似的方式振动,即以准周期的规律变化,而且分形维数越大,这种准周期规律越显著。 采用同样的分析方法将表1数据代入式(6),当系统初始参数一定,特征尺度分别取2×10-11、4×10-11、6×10-11、8×10-11m时,系统法向振动位移波形、速度波形、相图如图4所示。 从图4可以得出: (1)法向振动位移与速度均随着特征尺度G的增大而增大,而且该法向振动同样呈现出高频微幅振动的规律; (2)通过与图3的对比不难发现,同样是表征粗糙表面的分形参数,分形维数对法向振动的影响比特征尺度的影响更加明显。 图4 不同特征尺度下的法向振动规律Fig 4 Normal vibration law under different characteristic scale (a)displacement waveform;(b)speed waveform;(c)phase diagram 当密封端面分形维数、特征尺度、摩擦因数一定时,分析了转速对系统法向振动规律的影响。转速分别取3 000、9 000、15 000、21 000 r/min时,系统法向振动位移波形、速度波形、相图如图5所示。 图5 不同转速下的法向振动规律Fig 5 Normal vibration law at different rotational speed (a)displacement waveform;(b)speed waveform;(c)phase diagram 从图5可以得出: (1)随着转速的增大,法向振动位移与速度均先增大后减小,并在转速的增大过程中,同样出现了拍振现象。通过进一步分析计算,当密封环转速在18 000 r/min(此时密封环面的平均滑动速度为67.86 m/s)时,密封端面出现共振现象。 (2)从相图可以看出,法向振动规律仍表现出准周期性,而且转速对这种准周期性的影响较大。同时,随着转速的增大,这种高频微幅振动表现得越强烈。 当摩擦界面分形维数、特征尺度、转速一定时,分析了摩擦因数对系统法向振动规律的影响。摩擦因数分别取0.2、0.4、0.6、0.8时,系统法向振动位移波形、速度波形、相图如图6所示。 图6 不同摩擦因数下的法向振动规律Fig 6 Normal vibration law under different friction coefficients (a)displacement waveform;(b)speed waveform;(c)phase diagram 从图6可以得出: (1)随着摩擦因数的增大,法向振动位移与速度均增大,而且同样呈现出准周期的高频微幅振动规律。 (2)尽管法向振动位移随摩擦因数的增大而增大,但摩擦因数对其的改变量却并不显著。因此,摩擦因数对法向振动位移来说不是一个敏感因素。 当密封端面分形维数、特征尺度、转速一定时,分析了摩擦因数对系统切向振动规律的影响,摩擦因数分别取0.2、0.4、0.6、0.8时,系统切向振动位移波形、速度波形、相图如图7所示。 从图7可以得出: (1)随着摩擦因数的增大,切向振动位移与速度均增大,而且以周期性的高频微幅振动规律变化。 (2)切向振动位移表现出明显的方向性,即切向振动位移与摩擦力方向一致,与运动方向相反。相比于摩擦因数对系统法向振动的影响,摩擦因数对切向振动的影响更加明显。 图7 不同摩擦因数下的切向振动规律Fig 7 Tangential vibration law under different friction coefficients (a)displacement waveform;(b)speed waveform;(c)phase diagram (1)基于分形理论建立了干气密封在干摩擦状态下考虑微观形貌与接触特性对宏观系统影响的两自由度摩擦振动系统模型。同时,根据描述粗糙表面轮廓曲线的W-M函数,构建了包含分形参数的密封端面法向位移激励。 (2)随着分形维数和转速的增大,法向振动位移与速度均先增大后减小;当密封环面分形维数在1.3左右,以及平均滑动速度为67.86 m/s时会导致密封端面在法向出现共振现象;随着特征尺度与摩擦因数的增大,法向振动位移与速度均增大。 (3)法向振动以准周期的高频微幅振动规律变化,相比于特征尺度,分形维数对法向振动的影响更加显著,而摩擦因数对法向振动来说不是一个敏感因素。 (4)随着摩擦因数的增大,切向振动位移与速度均增大,而且以周期性的高频微幅振动规律变化。然而,摩擦因数对切向振动的影响比对法向振动的影响要明显。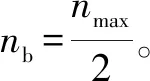
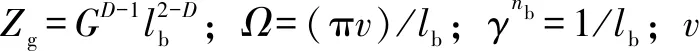
1.3 密封端面振动系统数学模型
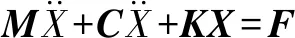
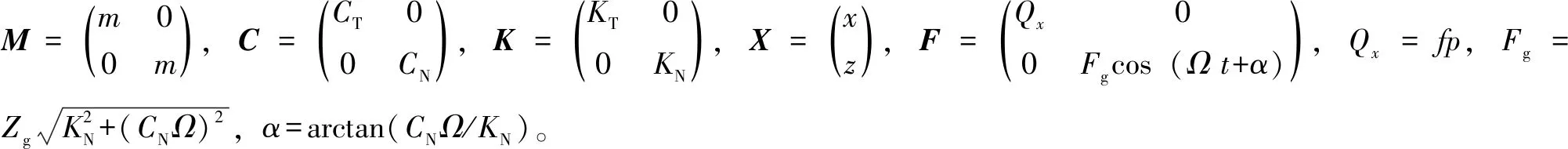
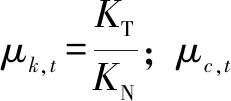
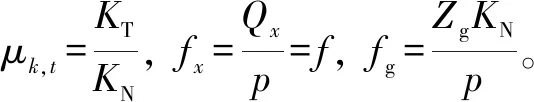
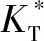
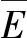
2 理论模型数值分析
2.1 分形维数对系统法向振动规律的影响
2.2 特征尺度对系统法向振动规律的影响
2.3 转速对系统法向振动规律的影响

2.4 摩擦因数对系统法向振动规律的影响
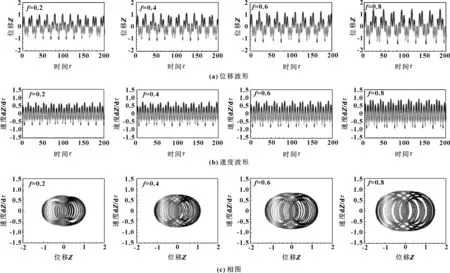
2.5 摩擦因数对系统切向振动规律的影响
3 结论
