双站极坐标法在混凝土坝变形监测中的应用

占晓明 李见阳 袁珊丽

（浙江华东测绘与工程安全技术有限公司，浙江 杭州 310014）

0.引言

大坝外部变形监测是大坝安全监测的重要内容，现有各类监测方法都必须满足国家或行业规范要求[1]。混凝土坝变形监测主要采用视准线、引张线、正倒垂线，其余还有交会法、大气或真空激光准直系统等[2]。垂线、引张线以及激光准直系统均需在大坝上布设永久观测仪器，施工过程复杂，成本较高。视准线和交会法一般采用高精度全站仪，仅需布置工作基点和监测点，观测方便，操作简单，成本较低，非常适用于各类中小型大坝。视准线法，因其原理限制，测线需布置成直线，且测线长度一般不宜过长，因此其仅适用于中小型的重力坝或闸坝等，不适用于拱坝和大范围的边坡监测。交会法因其具有成本低、适用条件广、操作简便等优点，在水电站大坝及边坡的变形监测中广泛应用。

单站极坐标法作为交会法的一种，其外业操作简便，成果计算简单。但由于单站极坐标法受仪器精度限制，难以满足混凝土坝变形监测精度要求。如采用TS30 全站仪，工作基点距离监测点300m 时，监测点位移理论估算精度为±1.4mm，无法满足《混凝土坝安全监测技术规范DL/T 5178-2016》的要求。

双站极坐标法作为单站极坐标法的改进方法，其较单站极坐标法增加了检核与校验条件，提高了可靠性和观测精度[3]。但双站极坐标法的实测精度能否满足《混凝土坝安全监测技术规范DL/T 5178-2016》的要求，相关研究较少。本文以宝泉水电站下水库大坝变形监测为例，从数据预处理、理论精度估算、实测精度分析等方面对该方法的可行性、适用条件进行了分析，得出一些结论，供类似工程参考。

1.数据预处理

实测变形监测数据中包含了真实变形及测量误差，如不进行预处理，进行精度分析时，其中误差统计结果会明显失真。常用的数据预处理方法是对数据序列进行数据平稳性检验（趋势性判断）和趋势项剔除。

1.1 平稳性检验

变形监测数据是时间序列的一种，时间序列的平稳性是进行时间序列分析的一个基本前提，尽管实际生活的多数时间序列都符合平稳性（广义平稳）条件，但在通常情况下仍需对数据序列进行平稳性检验。

平稳性检验的方法有许多种，应根据变形监测成果序列的实际情况选择合适的平稳性检验方法。

本文介绍一种简单实用的平稳性检验法，该方法只涉及一组数据，而不需要假设数据的分布规律[4]。该方法是平稳性非参数检验方法的一种，也称游程检验法，其使用简单，非常适用于变形监测数据的平稳性检验。

在保持随机序列原有顺序的情况下，游程定义为具有相同符号的序列，这种符号可把观测值分成两个相互排斥的类。例如观测序列的值xi（i=1，2，…N）其均值，用符号“+”表示xi≥，而“-”表示xi＜。按符号“+”和“-”的出现顺序将原系列写成如下形式，例如

“+”号和“-”共14个，分7个游程。每个游程的长短在这里并不重要。游程太多或太少都被认为是存在非平稳趋势[4]。游程检验所判断的原假设为：“样本是平稳的”。采用的样本统计量有：N1=一种符号出现的总数；N2=另一种符号出现的总数；γ=游程总数。

当任意一种符号出现的总数超过15 时，即可以基于正态分布来进行稳定性检验。

构建统计量：

对于α=0.05 的显著水平，如果|Z|≤1.96（两倍中误差），则可接受原假设，数据是平稳的（没有趋势性），否则就拒绝原假设。

1.2 趋势项剔除

1.2.1 差分法

差分法是实践中最常用的剔除趋势项的方法，主要原理为各期成果间依次相减，得出每期的变化量，再以每期的变化量为样本统计其中误差。

差分法仅适用于趋势项比较平稳的情形，无差别地使用该方法同样会导致结果失真，统计精度偏低。

变形监测成果精度分析中，通常是基于每期成果的变化量进行。其基本原理即是通过差分法消除各期观测成果间的误差“同类项”。但是，误差的成因十分复杂。不同期次的观测成果，其误差影响因素（监测人员、监测仪器、监测环境）不可能完全一致。因此，通过差分不能完有效剔除趋势项。

1.2.2 滑动平均法

为了更好地表示测量结果，抑制误差的影响，常对动态数据进行平滑和滤波，即认为小区间数据是平稳的，而对其进行某种局部平均，以减少误差影响[5]。沿全长N 个数据逐一小区间上进行不断局部平均，即可得出较平滑的测量结果[6]。其处理步骤如下：

第一步：设观测值｛x1，x2，…xn｝，如果周期为偶数，如d=2q，则有：

如果周期是奇数，如d=2q+1，则用公式（6）：

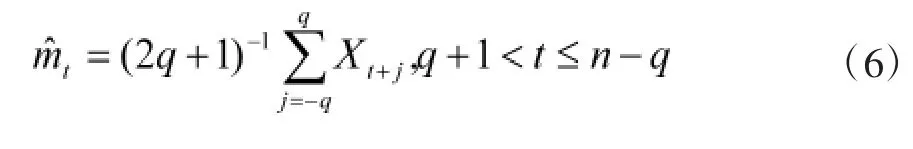
第二步：估计周期项

对于k=1，…，d，计算偏差：

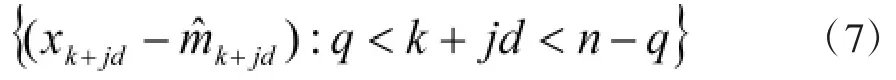
由于偏差平均值之和不为零。故sk的估计：

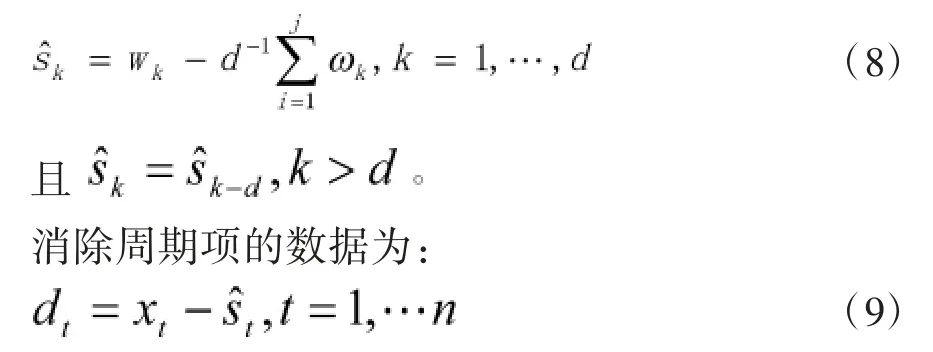
2.精度计算方法

2.1理论精度估算

宝泉水电站下水库变形监测采用双站极坐标法，其原理是两次独立单站极坐标法成果取算术平均。

双站极坐标法的理论估算精度估算公式为：

式中，S1为工作基点A至被监测点的水平距离；S1为工作基点B至被监测点的水平距离；mα为测角中误差，取仪器标称测角精度：±0.5″；ms为测边中误差，可根据本项目采用的徕卡TS30 全站仪标称测距精度±（0.6mm+1ppm×S）进行估算；S为测站至监测点距离，ρ=206265。

该理论精度估算方法只考虑了监测方法和监测仪器，忽略了监测人员和监测环境的影响，因此其理论预估精度通常要高于实测精度。但是，在短距离测量情况下，全站仪的实测精度通常要优于标称精度。综合以上两方面因素，应用公式（10）估算的理论精度与实测精度基本一致。

从理论精度估算公式可以看出，双站极坐标法精度主要受测角精度、测距精度以及测站至测点间距离影响。在仪器标称精度确定的情况下，测角精度和测距精度主要受距离长短影响。因此，双站极坐标法主要通过控制工作基点与监测点间距离来控制误差。

当监测点距离两个工作基点距离均为300m 时，监测点位移的理论精度刚好满足《混凝土坝安全监测技术规范DL/T 5178-2016》要求±1.0mm。

由此可见，当监测点至测站距离不长时（一般不超过300m）时，采用高精度全站仪的双站极坐标法理论精度可以满足混凝土坝变形监测要求。

宝泉水电站下水库各大坝变形监测点至A 工作基点（编号A2）的距离为52.3m～436.8m，各大坝变形监测点至测站B（编号L2-1）距离为130.5m 至478.9m，其理论预估精度统计表（如表1 所示）。由表1 可见，变形监测点的理论预估精度为±0.9mm～1.1mm，基本满足《混凝土坝安全监测技术规范DL/T 5178-2016》的要求。

表1 下水库大坝变形监测理论预估精度统计表

2.2实测精度计算

经过趋势项剔除的数据，按照公式（11）进行统计其中误差用于精度评估。

式中，v为改正数，取多期算术平均值与各期观测值之差，即νi=xi-x。

3.实例分析

宝泉水电站位于河南省新乡市，工程由上水库大坝工程、下水库大坝工程、引水发电系统、开关站等几部分组成。其中，下水库大坝为浆砌石大坝改建的混凝土大坝，坝高107.5m，工程建于1974 年，1994 年建成，主要以灌溉为主，运行至今大坝和库岸边坡安全稳定，没有出现任何问题。

为监测大坝变形，在坝顶防浪墙上布设了12 个变形监测点。以整个溢流坝段为分界段，将12 个位移监测点分别布置在大坝的左右坝段，每两个监测点间距为30m，其中D2-01～D2-06 布置在左坝段，D2-07～D2-12 布置在右坝段。测点布置图（如图1 所示）：

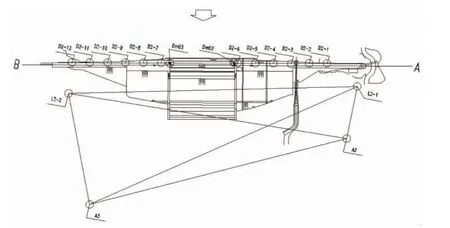
图1 下水库大坝变形监测点布置图

图2 D2-4、D2-5、D2-6 上下游方向过程线图

下水库大坝变形监测自2018 年1 月改用徕卡TS30 高精度全站仪双站极坐标法进行监测，工作基点分别为A2、L2-1，监测频次为每月2 次，监测过程中严格进行了气象参数测定，成果计算时采用两次单站成果取算术平均。

选取2018 年1 月至2020 年7 月，共计60 期的变形监测成果进行分析。其中D2-4、D2-5、D2-6 三个监测点上下游方向的过程线（如图2 所示）。从图2 可见，D2-4、D2-5、D2-6 三个监测点上下游方向最大变化幅度约20mm，月变化量平均3mm～5mm，且存在明显的趋势性变化，需对监测序列进行预处理。

本文先采用游程检验法对成果序列进行平稳性检验，检验结果（如表2 所示）。检验结果显示：所有测点的监测成果序列均未通过平稳性检验，存在趋势性位移。

表2 下水库大坝变形监测序列平稳性检验结果

根据上述检验结果，分别采用差分法和滑动平均法对成果序列进行趋势项剔除，再统计各点理论预估中误差、采用不同方法剔除了趋势项后的中误差，各项中误差统计（如表3 所示）：

表3 下水库大坝变形监测精度统计表

由表3 可见，各点理论精度估算值为±0.9mm～±1.1mm。趋势项剔除前，实测中误差为±2.2mm～±3.8mm，明显低于理论预估精度。采用差分法进行趋势项剔除后，其中误差为±1.8mm～±2.5mm，而采用滑动平均法的中误差为±0.9mm～±1.2mm，后者与理论预估中误差基本一致。可见监测成果中有显著趋势性位移时，滑动平均法比差分法效果更好。

从表3 可见，采用滑动平均法趋势项剔除后的实测中误差为±0.9mm～±1.2mm，多数测点实测中误差略微超过混凝土坝安全监测技术规范中要求的混凝土坝外部变形监测精度优于±1mm。主要原因为监测点距离工作基点较远（至少1 个工作基点距离监测点超过300m）。

实践中，除规范要求精度外，还应根据变形量综合确定监测方法是否可行。宝泉水电站下水库大坝虽然从水电站管理角度定为混凝土坝，但其是在浆砌石重力坝的基础上改造而来。其坝高91m 以下为原浆砌石坝体，只有加高的26m 坝体为混凝土坝体。因此宝泉水电站下水库大坝较常规的混凝土重力大坝变形大，实测最大变形幅度约20mm。

大坝变形监测实践中，一般要求监测成果的误差要显著小于变形量。国际测量工作者联合会（FIG）变形监测研究小组提出测量误差应小于变形量的1/20～1/10，国内外部分学者提出应在1/10～1/4 之间[7]。

从表3 统计中误差可见，实测精度达到变形量的1/22～1/16，完全满足上述要求，可见双站极坐标法进行混凝土坝变形监测是可行的。

4.结论

本文基于实测数据，对双站极坐标法进行理论估算精度和实测精度统计分析得出以下结论：

（1）双站极坐标法具有操作简便、计算简单、成果可靠、成本低等优点，采用双站极坐标法进行混凝土坝变形监测是可行的。

（2）采用极坐标法进行混凝土坝变形监测时，应严格控制监测点至工作基点距离，一般不超过300m。超过300m 时，应进行专项技术设计，并核算监测点的位移精度是否满足相应规范要求。

（3）当变形监测成果中存在显著趋势性位移时，进行成果实测精度分析前应进行数据预处理，剔除成果中的趋势项。滑动平均法比差分法的趋势项剔除效果更好。