压缩热效应对单晶硅密度测量的影响

钟家栋, 孙 斌, 赵玉晓, 马鑫钰, 张竟月, 张殿龙

(1.中国计量大学, 浙江 杭州 310000; 2.中国计量科学研究院, 北京 100029)

1 引 言

密度的精准测量对国民经济和国防科研的发展有重要影响[1,2],单晶硅球作为密度的量传基准,对其进行高精度的测量十分关键。固体基准单晶硅球体的密度测量主要分为绝对测量法与相对测量法[3]。绝对测量法是指使用非接触相移干涉法测量单晶硅球体积,然后使用载有质量副基准的真空比较器测量单晶硅球的质量,从而计算其密度值,对密度的绝对测量其实就是对质量和长度的绝对测量。单晶硅球体密度绝对测量法测量精度高,但是存在仪器昂贵、实验周期长等缺点[4]。相对测量法主要是指液体静力称重法、磁力称重法和稳态悬浮法,通过和一个已知密度的标准单晶硅球体进行比较,进而计算待测单晶硅球的密度[4]。该类方法比绝对测量法更容易实现,是绝对测量法的重要补充,对单晶硅球体密度实现等精度的量值传递。在液体静力称重法中,由于液体表面张力的影响,密度量值传递的准确度受到限制,难以提高密度量传的准确性[5]。磁力称重法为了消除直接称量带来的液体表面张力[5,6],使用非接触的磁力称重,但是由于壳体和工作液体的磁效应,目前测量不确定度只有5×10-6。稳态悬浮法是将待测固体浸没于液体中,通过调节液体的成分、温度以及压强来使得待测固体稳态悬浮于液体中,通过此时待测固体所受重力与浮力间的平衡来计算固体密度[7]。改变液体的比例成分对其密度影响较大,配置成功之后一般就保持不变了,相当于密度的初步调节。温度对液体密度的影响相对液体成分更好控制,但是考虑到温度传递速度较慢,每次调节都需要2 h的等待,所以将其作为粗调密度的方法。压强变化对液体密度的影响不仅微小而且反应快,因此可视为密度的微小调节,压强悬浮法目前也是最为广泛的研究方法[8]。

稳态悬浮法普遍采用改变静压力与温度的方式来进行对近单晶硅液体(DSL-2329)密度的微量调节。由于压缩热效应,在微调时改变静压力也会使得液体温度发生变化,间接导致液体密度改变,从而影响单晶硅球密度测量结果。本文通过实验分析,探究压缩热效应对DSL-2329液体温度的影响。此方法适用于对各种形状的纯硅材料进行密度测量。

2 理论原理

近单晶硅液体(DSL-2329)在工作液体成分比例恒定时,由液体热物理性可知,工作液体(DSL-2329)的密度可以表示为:

ρl(t,p)=ρl(t0,p0)[1-γl(t-t0)+

Kl(p-p0)]

(1)

式中:γl和Kl分别为液体的等压热膨胀系数和等温压缩系数;t0和p0分别为参考温度与压强,一般分别取20 ℃和101 325 Pa；ρl(t0,p0)为工作液体在参考温度与压强时的密度。

单晶硅球体的密度与温度和压强的关系可以表示为:

ρSi(t,p)=ρl,Si(t0,p0)[1-γSi(t-t0)+

KSi(p-p0)]

(2)

式中:ρl,Si(t0,p0)为单晶硅球体在参考温度与压强下的密度;γSi和KSi分别为液体的等压热膨胀系数和等温压缩系数。

稳态悬浮法通过调节容器内温度与压强,使得单晶硅球体S1和S2分别在各自的温度压强条件下稳态悬浮于液体DSL-2329中。那么,在平衡状态下,硅球和液体的密度相等:

ρl(t1,p1)=ρSi1(t1,p1)

(3)

ρl(t2,p2)=ρSi2(t2,p2)

(4)

式中:t1,p1分别为硅球S1稳态悬浮时的温度与压强；ρl(t2,p2)为硅球S2稳态悬浮时的温度与压强。由式(1)～式(4)可推算出2个单晶硅球体之间相对密度差为:

(5)

由式(5)可知,对于相对密度差,温度项的影响值远大于压强项,通过线性公式变换,忽略掉高次小量,可以式(6)计算2个单晶硅球的相对密度差:

(Kl-KSi)(p2-p1)

(6)

式(6)就是经典的压强稳态悬浮法公式。其中单晶硅材料的热膨胀系数和压缩系数均远小于液体DSL-2329。其中,KSi=(1.022±0.01)×10-11Pa-1,γSi=(7.67±0.1)×10-6K-1。而液体DSL-2329的压缩系数Kl和膨胀系数γl由式(7)和式(8)测量:

(7)

(8)

使用高精度的恒温水浴控制整个环境在非常小的温度波动下,使得2个单晶硅球体的温度t2和t1相等,通过控制压强,使得2个单晶硅球体分别到达自己各自的稳态悬浮状态,由单晶硅材料和液体DSL-2329的物理系数以及各个状态下的压强可以计算2个单晶硅球相对密度差:

(9)

在用稳态悬浮法测量的时候,向液体施加压强可以增大液体密度,但是同时也会导致液体温度升高,而温度升高会导致液体密度下降,因此加压之后会导致短时间内施加压强的效果被抵消一部分,这就是压缩热效应。考虑到压缩热效应的存在,施加压强后不能立即获得该压强下的液体密度,而是需要等待温度达到平衡。为了消除压缩热效应,获得稳定的平衡状态,需要探究压缩热效应的大小与影响时间长短。

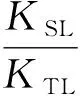
在衡熵条件下,压强变化导致液体的温度变化可以这样计算:

(10)

式中:T为液体DSL-2329温度;cp为液体的比热容;γl为热膨胀系数;ρl为液体密度。

由于压强升高引起的温度变化也会影响液体的密度值。两者共同影响下液体密度的变化值与仅仅由压强变化引起的密度值变化值的比值即液体绝热压缩率与等温压缩率的比值:

(11)

式中:Δρp为仅由压强变化带来的密度变化值;Δρt为仅因压强升高导致的温度上升进而产生的液体密度变化值。ΔρpΔρt可以分别为:

Δρp=KTLΔp

(12)

Δρt=-γlΔt

(13)

式中Δp,Δt分别表示压强和温度的变化值,由式(10)可以求得由于压强变化引起的温度变化值:

(14)

通过式(1)～式(14)可得:

(15)

3 实验结果

测量系统基本构造如图1所示,在恒温实验室中,工作液体DSL-2329和2个待测的单晶硅球体置入封闭的容器中,恒温水浴为整个环境提供稳定的温度环境,铂电阻温度计实时测量恒温水浴中的温度,同时向计算机传输水浴的温度信息,验证实验时温度波动在允许范围内。CCD相机采用物方远心光学镜头,拍摄单晶硅球体在DSL-2329液体中的图像,向计算机传输图像信息。压强控制器负责向封闭容器提供额外压强,同时向计算机传输压强数据。使用C++语言编写基于对话框的MFC工程:其中编写的图像处理程序检测硅球的竖直位移情况,实时显示硅球竖直位移值;MFC工程编写的串口通信模块,实时显示压强值,并且分析硅球的竖直位移值对压强进行输出指令,调控压强大小,使得单晶硅球体在制定竖直高度获得稳态悬浮状态。

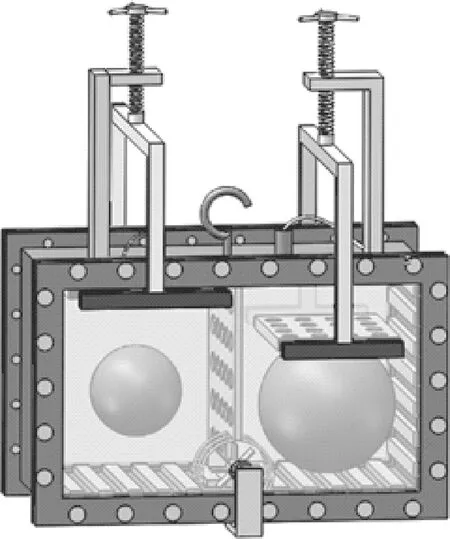
图1 比较容器示意图Fig.1 Comparing container diagrams

单晶硅比较容器是用来盛放硅球和工作液体DSL-2329的,将液体装入比较容器,再将2个待比较的单晶硅球体浸没于液体中,封闭容器。整个容器需要置入恒温水浴中,而且将会施加一定压强,因此密封性需要足够好。容器采用整块不锈钢材料线切割制成,前后部分使用钢化玻璃便于观察单晶硅球体的运动状态。玻璃与不锈钢框架之间使用聚四氟乙烯衔接,因为为聚四氟乙烯具有稳定的化学特性,能抗化学腐蚀,不溶于有机溶液。不锈钢内侧垫有一层聚四氟乙烯,这是为了保护单晶硅,防止硅球在容器内部上浮下沉时与不锈钢材料进行撞击,避免单晶硅材料的磨损。整个容器经过加压测试密封性后才能使用。

如图1所示,在容器中间使用四聚氟乙稀的隔板将2个硅球隔开,这是为了防止两者运动时互相影响。为了使工作液体均匀分布在容器中,中间的隔板需要打孔,而且内部安装1个磁力棒,这样在实验之前在容器外部使用磁铁转动内部的磁力搅拌棒,可以使内部液体快速均匀分布。为了在实验过程中,待测单晶硅球体的运动状态不受另1个的影响,需要控制另1个硅球静止不动。因此给比较容器安装了磁力升降杆,在放入工作液体与待测单晶硅球体后,封装容器之前,将2块嵌有磁铁的四聚氟乙稀板子放入容器。镶嵌的磁铁外部包裹着四聚氟乙稀保护磁铁。在容器外部的升降杆也镶嵌磁铁,靠磁力吸引着内部的磁铁,从而带着容器内部的四聚氟乙稀板上下运动。当调节压强使得1个硅球的稳态悬浮时,另1个硅球需要依靠磁力升降杆将其压于容器底部,防止干扰待测的硅球。经过抗压测试,该容器可以在加压80 kPa的条件下正常工作。图2所示为恒温水浴装置图。

图2 恒温水浴装置Fig.2 Constant temperature water bath device

恒温水浴用于放置密度比较容器,针对单晶硅球密度测量的高精度技术要求。该设备内部采用双循环水浴恒温,尺寸为1 219 mm×1 118 mm×559 mm,温度控制范围是0～110 ℃,温度调节的分辨率为0.002 ℃。在精密恒温器里的环形加热器连接着一个直流电源,该电源的输出是由基于计算机的PID算法控制,这样放置在测量元件附近的温度传感器输出的结果就与精确恒温器的目标温度一致。一个搅拌棒被放置在冷却线圈中。为了防止加热和冷却的水直接和测量元件接触,一个防护板被安装在测量元件附近。整个水浴放置在隔振台上,比较容器放置水域中。

为了准确测量工作液体的膨胀系数,使用振动管密度计测量液体在不同温度下的密度值,使用式(10)计算。由于最后使用的测量环境温度为21.200～21.300 ℃,测量参考温度设为21.200 ℃。使用振动管密度计测量工作液体在21.000～21.500 ℃范围内间隔0.05 ℃的密度值,计算其膨胀系数,如图3所示。

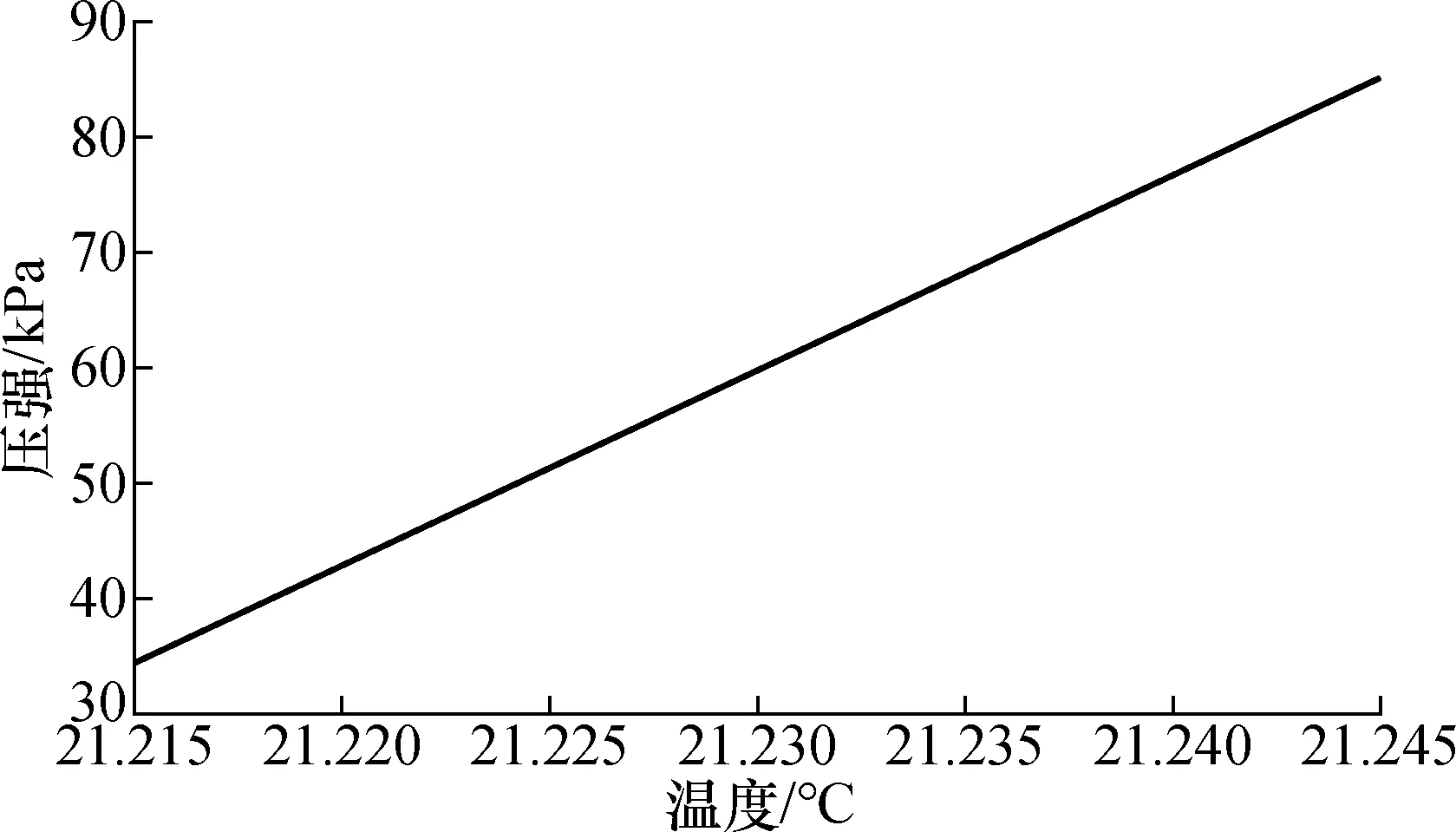
图3 液体密度不变时温度与压强的线性关系Fig.3 Linear relationship between temperature and pressure with constant liquid density

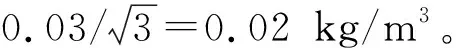
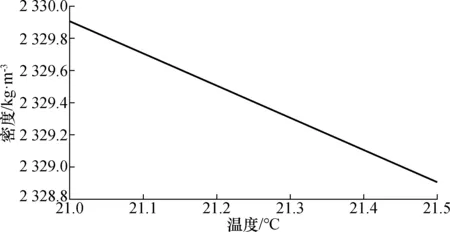
图4 液体DSL-2329在不同温度下的密度值Fig.4 Density of liquid DSL-2329 at different temperatures

得到液体DSL-2329的膨胀系数之后,利用式(8)计算液体的压缩系数。对同一个硅球进行测量,控制压强使得在不同温度下硅球保持稳态悬浮,这样液体DSL-2329的密度可视为保持不变,满足式(8)的使用条件。如图5所示为液体密度保持不变时温度与压强的线性关系图。

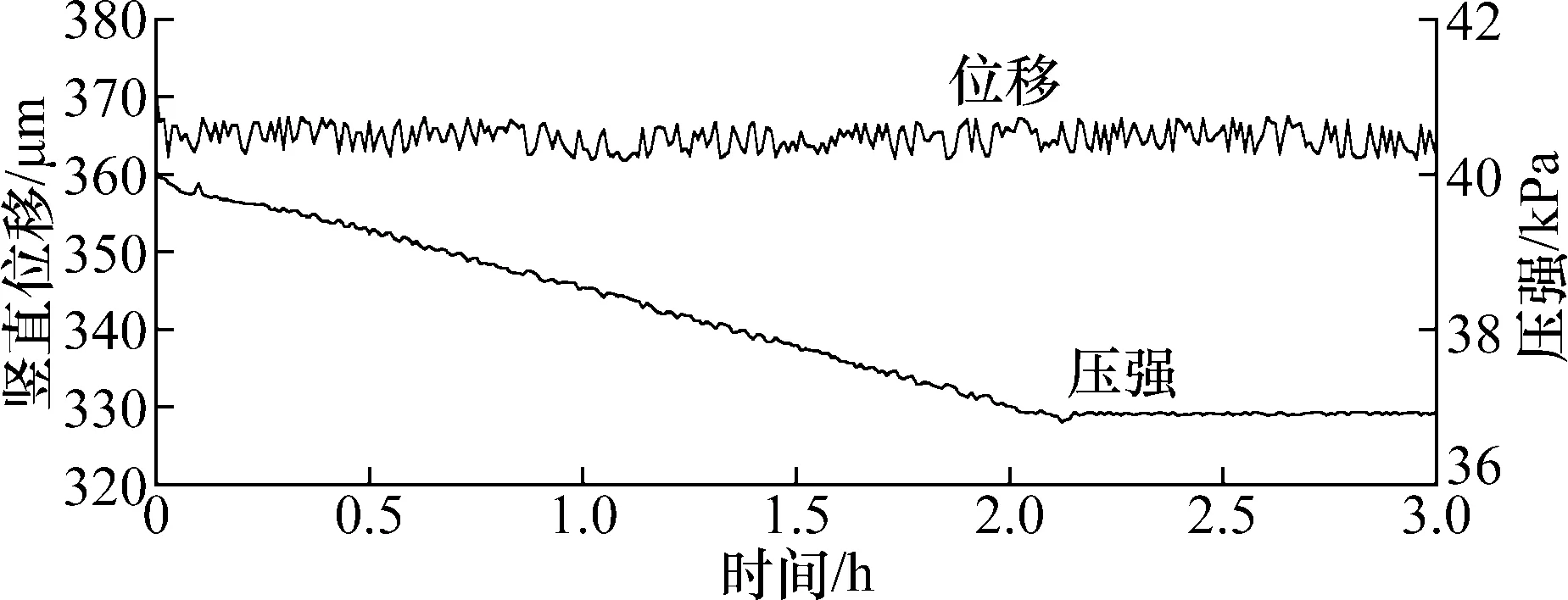
图5 压缩热效应对稳态悬浮的影响Fig.5 Effect of compression thermal effect on steady suspension

经过式(8)计算可以得到液体DSL-2329的压缩系数Kl为(5.10±0.05)×10-10Pa-1。

由式(10)～式(15)可知通过等温压缩系数Kl和比热c的值可以计算出(∂T/∂p)s=0.15 μK·Pa-1以及1.389 2KSL=KTL。这说明增加1 Pa压强导致液体温度升高0.15×10-4℃,这样增加1 Pa压强导致的液体密度变大相当于产生0.72 Pa的效果,然后在恒温水浴的作用下,升高的温度会慢慢减小,最后才能产生1 Pa压强的加压效果。这期间可视为硅球的密度不变,温度减小的过程中,同时减小压强可以使得硅球稳态悬浮于同一高度,保证液体的密度始终等于硅球的密度。这样就可以用压强的变化反应温度的变化。

使用图形子系统检测硅球S2的竖直位置,通过调节压强改变硅球的悬浮状态。经过一系列测试得知硅球S2约在40 kPa可以悬浮。控制压强到达 20 kPa,硅球沉与容器底部不动,然后将压强快速升至42 kPa,可观察到硅球快速上升,调节压强大小使硅球稳态悬浮于液体DSL-2329中时,调控压强使得硅球稳定在该位置,可以发现,压强与温度一直在缓慢减小最后趋于稳定,如图6与表1所示。经过实验可以发现,压缩热效应导致一开始需要施加更多的压强以弥补温度升高造成的影响。然后在恒温水浴的作用下,温度逐渐下降,为了保持硅球悬浮于同一高度,即保持密度恒定,需要减小压强。理论压强与实际压强约差3 kPa,可以通过加入液体精密测温模块来检测压缩热效应带来的影响,经过压缩热效应后的单晶硅密度测量结果与未经过压缩热效应的密度测量结果约有1.25×10-4kg/m3的误差。最后发现,经过2.5 h,压强趋于稳定,即压缩热效应产生的温度被恒温水浴抹平,此消除误差。

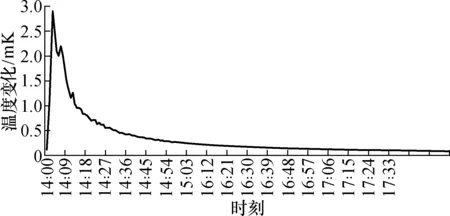
图6 压缩热效应温度变化曲线Fig.6 Temperature curve of compression thermal effect

表1 压缩热效应对压强的影响Tab.1 Effect of compression heat on pressure

4 结 论

实验结果表明,压强变化量越小,测得的恒熵压缩系数与液体恒温压缩系数的比值与理论值0.72越接近,压缩热效应带来的温度变化不可忽略,带来的温度变化需要大概需要2.5 h才能消除,效果换算为压强为增加压强的28%。为了减小压强变化带来的压缩热效应,可以减小压强的变化量,这样就需要先调试硅球悬浮,得到压强估计值,然后将压强值调至估计值附近,等待3 h后再进行细微的压强调控。这样做可以避免压强的大幅度变化,减小压缩热效应的影响。

[参考文献]

[1] 郭立功, 刘子勇, 罗志勇, 等. 容量密度计量领域纯水密度国际研究现状[J]. 计量技术, 2012, (11): 28-30.

[2] 罗志勇. 质量自然基准的研究进展及发展方向[J]. 计量学报, 2004, 25(2): 138-141.

Luo Z Y. The Progress and Development Trend of Mass Natural Standard[J].ActaMetrologicaSinica, 2004, 25(2): 138-141.

[3] Luo Z Y,Gu Y Z,Zhang J T,etal. Interferometric Measurement of the Diameter of a Silicon Sphere With a Mechanical Scanning Method[J].IEEETransactionsonInstrumentation&Measurement, 2010, 59(11): 2991-2996.

[4] 罗志勇,王金涛,刘翔,等. 阿伏加德罗常数测量与千克重新定义[J]. 计量学报, 2018, 39(3): 377-380.

Luo Z Y, Wang J T, Liu X,etal. Avogadro Constant Determination and Kilogram Redefinition[J].ActaMetrologicaSinica, 2018, 39(3): 377-380.

[5] 顾英姿, 陈朝晖, 许常红, 等. 液体静力称量法液体密度测量及其不确定度评定[J]. 计量技术, 2006, (6): 8-11.

[6] 顾英姿, 罗志勇, 陈朝晖, 等. 液体表面张力对静力称量法固体密度测量的影响[J]. 计量学报, 2013, 34(3): 247-250.

Gu Y Z, Luo Z Y, Chen C H,etal. Study on Influence of Liquid Surface Tension on Solid Density Measurement by Hydrostatic Weighing[J].ActaMetrologicaSinica, 2013, 34(3): 247-250.

[7] Waseda A, Fujii K. Density comparison measurement of silicon by pressure of flotation method[J].IEEETransactionsonInstrumentation&Measurement, 2001, 50(2): 604-607.

[8] 刘子勇, 王金涛, 许常红, 等. 基于压浮原理的单晶硅球密度比较测量方法研究[J]. 计量学报, 2013, 34(2): 97-100.

Liu Z Y, Wang J T, Xu C H,etal. Research on Comparison Measurement of Single-crystal Silicon Sphere Density Based on Pressure Floatation Method[J].ActaMetrologicaSinica, 2013, 34(2): 97-100.