不同开裂状态下预应力混凝土连续箱梁受力性能评估试验研究

李克忠，曹国辉，杨李根

（1.湖南大学设计研究院有限公司，湖南长沙，410082；2.长沙华艺工程设计有限公司，湖南长沙，410000；3.湖南城市学院土木工程学院，湖南益阳，413000；4.湘潭大学土木工程与力学学院，湖南湘潭，411105）

箱形截面具有良好的结构性能，在现代桥梁建设中得到广泛应用。随着道路等级提高和交通功能的变化，在城市立交桥和高架桥中不断采用钢筋混凝土箱梁桥，并趋于采用带横向大悬臂的横断面形式。然而，近几年来对箱梁桥进行调查发现，不少箱梁桥出现许多较宽裂缝，甚至一些运行时间不长的预应力构件也出现此类情况[1-2]。人们就这些裂缝对桥梁结构安全性的影响、结构的承载能力等进行了大量研究，如：CAO等[3]进行了开裂状态下简支箱梁的弯曲破坏试验研究；张志权等[4]研究了混凝土箱梁桥底板纵向裂缝对结构整体受力性能的影响；王海军等[5]从动力特性方面研究了裂缝对预应力混凝土连续箱梁安全的影响；SHENA 等[6]研究了初始裂缝对1 座60 年历史的箱梁桥受力的影响；WANG等[7]分析了预应力混凝土箱梁顶板横向裂缝对结构受力的影响。针对开裂状态下预应力连续箱梁桥的受力评估，国内外学者和工程技术人员也开展了研究，如：王凌波等[8]基于裂缝统计特征参数，建立了预应力连续箱梁桥裂后计算模型，利用承载力折减系数评估结构的剩余承载能力；徐向锋等[9]对预应力箱梁裂后的刚度分布特性进行了研究，提出了箱梁裂后刚度损伤评估方法；张勇夫[10]通过对梁端预应力张拉过程进行计算模拟，分析了预应力张拉过程中梁端应力变化并评估了梁端底板斜向裂缝对桥梁结构整体受力的影响；林贤坤等[11]研究了基于运行试验模态分析的模态挠度法应用于桥梁状态评估的可行性与有效性；HU 等[12]对扭转和弯曲载荷单独作用和联合作用情况下开裂箱梁的残余承载力评估进行了研究，得出了弯扭联合作用下的评估方程；FISCHER等[13]通过使用3D 有限元模型和物理非线性分析方法并结合现场调查对当地1座箱梁桥进行了系统评估。总体来说，这些评估方法比较复杂，很难简单、快速地初步估算开裂桥梁的受力情况。为此，本文作者对三跨预应力混凝土连续箱梁模型进行试验，得出以弹性计算结果估算开裂结构受力状态的修正系数，并提出裂缝宽度比值与承载率的函数关系，以便对桥梁实际受力状态、承载潜力和安全性进行初步估算和评估。

1 模型试验概况

1.1 模型概况

模型比例为1：4，模型横断面为等截面单箱单室混凝土箱梁，顶板宽为3.00 m，底板宽1.35 m；两端及中间支座位置设置横隔板，每跨8.16 m，共3 跨，边墩支座中心至梁端距离为0.2 m，总长24.88 m。模型平面如图1 所示，模型截面尺寸及配筋如图2 所示。模型箱梁的混凝土材料为C40，箱梁模型非预应力筋采用HRB335级钢筋，共配置48 孔1φs15.2（即公称直径为15.2 mm 的钢绞线，1个孔道中布置1 束）预应力筋束，其中26 孔布置体内预应力筋，20孔布置体外预应力筋，2孔布置临时索。钢筋的力学性能见表1，混凝土的力学性能见表2。

图1 模型1/2平面图Fig.1 Plan of 1/2 box girder model

图2 模型截面尺寸及配筋Fig.2 Section details and steel bar layout of box girder model

表1 普通钢筋的力学性能Table 1 Properties of steel bars

表2 混凝土的力学性能Table 2 Properties of upper plate concrete

1.2 测点布置

在边跨1/4 截面（A-A）和跨中截面（B-B，D-D和F-F）及中间支座截面（C-C和E-E）预埋振弦式应变计测试梁体内混凝土应变，如图3所示。在每跨1/4跨和3/4跨截面在底板位置对称安装百分表测量竖向挠度变化，百分表均安装在箱梁腹板与底板交接位置，每侧各1 个。另在每跨的L/2 截面翼缘板底部对称安装百分表测试悬臂端最大挠度（其中，L 为跨径），具体布置如图4 所示。采用500 kN 级球冠型桥梁专用橡胶支座，其中，中跨右端2号支座两侧为固定支座，其余均为滑动支座。

图3 控制截面体内混凝土应变计布置Fig.3 Layout of concrete strain in control section

图4 控制截面挠度测点布置Fig.4 Layouts of measuring points for control section

1.3 荷载的等效、加载方式及工况

根据相似原理，模型自重补载+二期恒载为1 100 kN，采用均布荷载的方式施加。汽车荷载效应采用等效集中荷载的方式模拟。按照应力等效原则将汽车荷载等效为集中力。

式中：Pm和Pp分别为模型和原型受到的集中荷载；Am和Ap分别为模型和原型的面积；σm和σp分别为集中荷载作用下模型和原型产生的应力。取应力相似系数Cσ＝1，几何相似系数Cl＝1/4，则由式（1）可知集中荷载相似系数Cp＝1/16。1.0 倍正常使用汽车荷载等效集中力为每跨跨中80 kN。

加载时在每跨跨中设置2个油压千斤顶，每个千斤顶连接1个电子秤，精确测试加载。主要加载工况如下：工况1，三跨同时加载；工况2，第一、第三跨同时加载。

1.4 预应力张拉

本试验预应力采用后张法实施，钢束采用穿心式千斤顶进行张拉，其锚固端采用锥形锚具。设置三弦智能型穿心式力传感器测量预应力张拉和加载过程中预应力筋的应力变化情况，张拉控制应力为0.75fpk=1 395 MPa（fpk为预应力钢筋抗拉强度标准值）。在张拉过程中，测试各钢绞线的有效预应力。预应力筋张拉时的基本参数如表3所示。

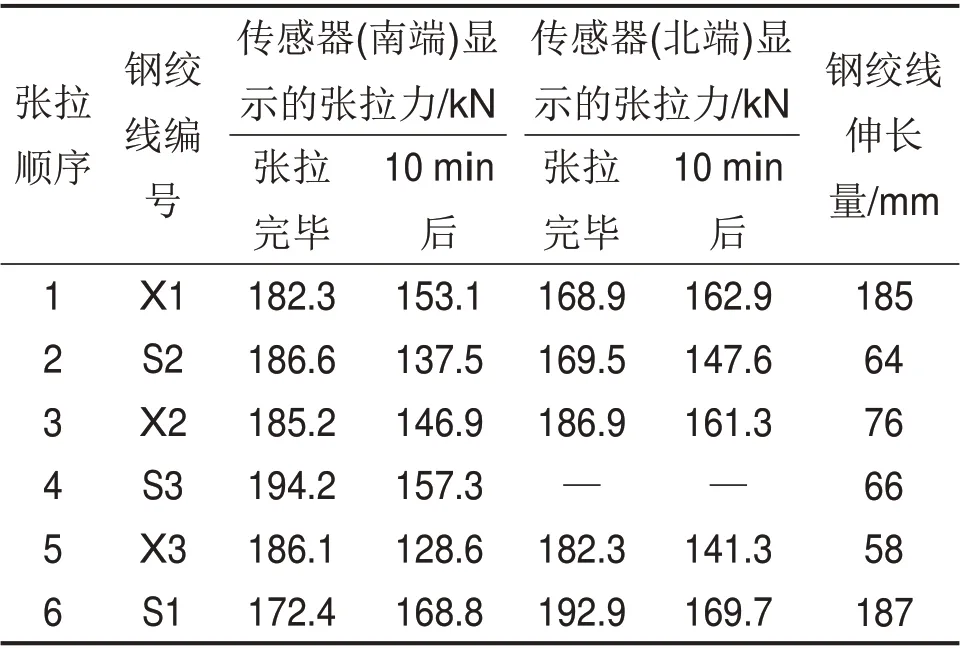
表3 预应力筋张拉时基本参数Table 3 Basic parameters of tension of prestressed tendon

2 理论计算

预应力混凝土结构在开裂前呈现弹性工作状态，而一旦开裂后，结构就开始表现出非线性特征。目前对混凝土结构分析计算主要有2 种方法[14]：1）弹性分析计算；2）非弹性分析计算。弹性分析计算简单易行，应用较广泛，但很难获得截面开裂后的真实结果。非弹性分析计算能得出较真实的结构受力，但计算复杂，一般需要专业人员才能进行，且费时费力，目前还很难普遍推广应用。本文建立弹性分析和非线性分析2 个模型，并将其梁体跨中挠度与特征截面混凝土应力应变计算结果与对应的试验结果进行分析、对比。

1）弹性分析模型。采用梁单元进行模拟，共33 个节点，32 个单元，如图5 所示。预应力筋按实际形状输入，预应力损失按规范[15]给定的方法自动进行计算。

图5 弹性分析计算模型Fig.5 Elastic calculation model

2）非弹性分析模型。采用有限元软件MARC进行分析计算，采用实体单元，按照对称原则取一半进行建模，中间采用对称支承，整个模型共计6 372个节点，6 360个单元，如图6所示。预应力筋采用桁架单元进行模拟，有效预应力按表3取值；混凝土弹性模量按表2取值。

图6 非线性分析计算模型Fig.6 Nonlinear calculation model

3 试验结果及分析

在施加完自重补载和二期恒载后，结构基本处于弹性工作状态，未出现裂缝。当集中荷载施加到300 kN（约正常使用汽车荷载的1.2 倍）时，模型出现受力裂缝，即开裂荷载为汽车荷载的1.2倍。

3.1 挠度分析

第三跨跨中荷载－挠度曲线如图7所示。从图7可见：当荷载大于300 kN时，随着荷载增加，模型挠度逐渐呈明显的非线性增大趋势；当荷载小于等于300 kN（开裂荷载）时，荷载－挠度曲线基本呈直线，即结构基本处于弹性受力阶段；当荷载大于300 kN 时，随着荷载增加，挠度增长速率变大，荷载－挠度曲线呈明显的非线性特征。第一、三跨跨中挠度的实测值与理论值见表4。

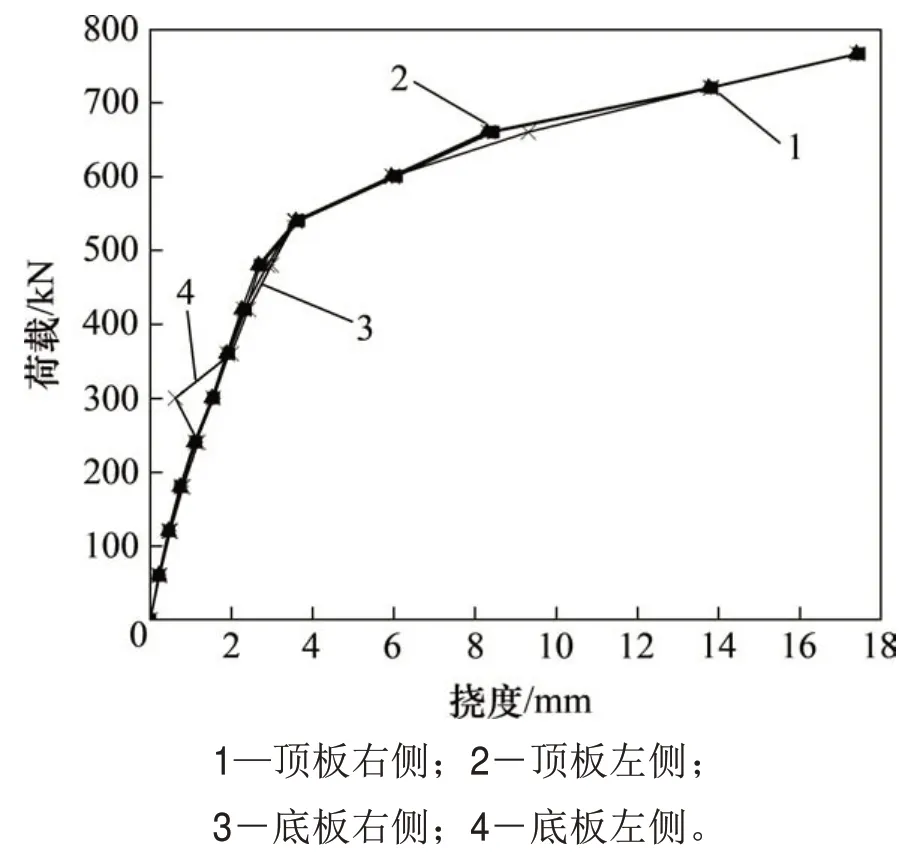
图7 第三跨跨中荷载与挠度的关系Fig.7 Relationship between load and displacement for the third mid-span

由表4可知：

1）模型开裂前，梁体跨中挠度弹性分析结果、非线性分析结果和试验实测结果三者之间基本吻合；模型开裂后，梁体跨中挠度弹性理论计算结果与试验实测结果的误差逐渐增大，而非线性理论计算结果和试验实测结果较吻合，验证了试验实测结果的可靠性。

2）开裂后，当加载量小于正常使用汽车荷载的2.0 倍时，工况1 和工况2 各跨中挠度试验实测结果与弹性分析结果之比基本在1.25～1.93 之间；当加载量增加至正常使用汽车荷载的3.0倍时，试验梁体跨中挠度急剧增大。根据有关部门对桥梁超载的统计结果，超载量基本在1.0倍设计荷载左右，因此，在桥梁运行期间，3.0 倍荷载基本不会出现。取2.0倍荷载以内的试验实测结果与弹性分析结果之比进行数理统计分析，得出采用弹性分析法对类似开裂桥梁估算其挠度时，其修正系数可取1.5～2.0。

3.2 混凝土应力分析

由图8 所示的支座处混凝土应变-荷载曲线可知：在荷载加载初期，荷载-应变曲线基本呈直线；随着荷载增加，当混凝土开裂后，应变呈现明显的非线性，部分区域的应变在开裂的瞬间发生突变。第一跨跨中截面和2号支座处截面应力理论值与实测值见表5。

由表5 可知：开裂荷载（1.2 倍汽车荷载）之前，特征截面应力的弹性分析计算结果、非线性分析计算结果和试验实测结果总体比较吻合，实测结果与理论结果的相对误差较小，部分截面相对误差稍大；开裂后，截面应力的试验实测结果与弹性分析计算结果之间的相对误差逐渐增大，在2.0倍荷载时两者之比大部分在1.3 至2.6 之间。选取1.2倍至2.0倍荷载之间的试验实测结果与弹性分析计算结果之比进行数理统计分析。由于试验结果中应变自身的离散性和局部性较大，故采用弹性分析法估算类似开裂结构应力时，其修正系数可采用1.5～2.5。

表4 梁体跨中挠度理论计算结果与试验实测结果Table 4 Theoretical results and measured results of displacement for mid-span of beam

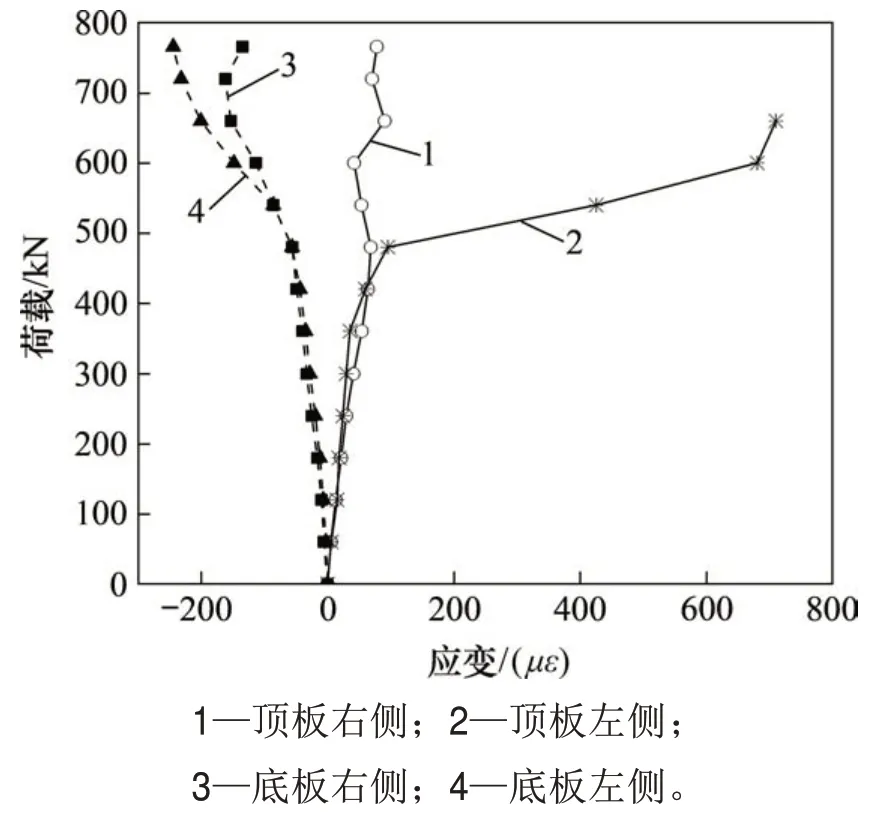
图8 支座处混凝土荷载-应变曲线Fig.8 Load-stress curves of concrete near support

4 基于裂缝宽度对承载能力进行评估

4.1 裂缝宽度的计算

“公路钢筋混凝土及预应力混凝土桥涵设计规范”[15]（以下简称“规范”）考虑了影响裂缝宽度的各主要因素。规范中裂缝宽度计算公式主要是以矩形、T 形和I 形截面试验构件的研究结果为基础得出；对于系数C3，并没有给出箱形截面受弯时的值，只是近似当作其他受弯构件的值，取1.0。而箱形截面因为截面钢筋布置、配筋率、构造和截面换算存在差异，并受施工质量、环境温度等影响，实际裂缝开展情况与规范公式计算结果存在差异[16]。实践结果[17-18]表明，对于混凝土箱梁结构的开裂情况及力学行为，直接借用矩形、T形等开口截面的研究结果描述是不准确的。所以，规范计算公式中部分参数需要根据混凝土箱形截面特点等进行修正，规范计算公式方法及影响因素基本不变。文献[19]通过预应力混凝土箱梁模型试验，分别对短期荷载作用和长期荷载作用下实测最大裂缝宽度与规范计算宽度进行对比，根据试验结果建议取系数C3=1.25。

表5 应力的理论值与实测值Table 5 Measured values and theoretical values of stress

4.2 基于裂缝宽度对结构承载能力进行评估

基于裂缝宽度对结构承载能力进行评估的试验方法如下。

1）根据试验结果得出各级荷载作用下各截面的实测弯矩M1；根据截面的预应力钢筋和普通钢筋的配置，按照规范计算截面的极限弯矩承载能力Mu，进而得出M1/Mu（承载率）。

2）根据规范的裂缝宽度计算公式，取修正系数C3=1.25，荷载按实际桥梁荷载取值，计算最大荷载作用下裂缝的宽度Wfk，由试验得出各级荷载作用下结构的裂缝宽度W1，进而得出W1/Wfk（即裂缝宽度比）。

3）根据各级荷载作用下M1/Mu（承载率）和W1/Wfk（裂缝宽度比）的关系，采用数理统计的方法对结果进行分析，拟合两者之间的关系。

模型在各级荷载作用下裂缝分布如图9 所示。图9中，裂缝主要集中在各跨跨中底板和支座负弯矩箱梁翼缘，部分底板裂缝扩展至腹板。裂缝F2，E1，E3，C2，C3，C1，C4，B5，B8 和B10 的宽度分别为0.333，0.193，0.234，0.097，0.083，0.178，0.114，0.063，0.147 和0.098 mm。各关键截面的截面承载率（M1/Mu）与裂缝宽度比（W1/Wfk）的关系见图10（a）和图10（b）。从图10（a）和图10（b）可以看出：各截面的承载率与裂缝宽度比值在早期两者基本呈线性关系；随着承载率增加，裂缝宽度比的增大速率逐渐大于承载率的增大速率；当裂缝宽度比大于1.0时，离散性较大，而在实际桥梁结构中，此种裂缝宽度出现的概率较小，因此，在选取承载率和裂缝宽度比进行拟合时，去掉裂缝宽度比大于1.0对应的各组数据，曲线拟合见图10（c），得出如下线性公式：

图9 箱梁模型裂缝分布Fig.9 Crack distribution of box girder model

图10 截面承载率与裂缝宽度比值的关系Fig.10 Relationship between crack width ratio and bearing capacity ratio

相关系数R=0.876 97。式（2）中，M1为实际结构所承受的弯矩；Mu为极限状态下结构所能承受的弯矩；W1为当前状态下结构的裂缝宽度；Wfk为极限状态下结构的计算裂缝宽度。

在桥梁的日常养护中，当前状态下结构的裂缝宽度W1可通过观测直接获得，Wfk根据桥梁设计资料和实际承载情况根据规范计算得出，此时，可根据式（2）得出结构在此裂缝宽度时的承载率，进而可得出桥梁的承载能力，由此可以判断桥梁运行时是否需要限载，若需限载，则限载量是多少等。

5 结论

1）对特征截面（支点、1/4跨、1/2跨截面）混凝土应力、应变及梁体跨中挠度弹性分析计算结果、非线性分析计算结果和试验实测结果进行对比，得出了结构开裂状态下以弹性分析计算结果估算结构挠度和混凝土应力的修正系数，即对类似开裂桥梁，采用弹性分析法估算其挠度时，其修正系数可取1.5～2.0，采用弹性分析法估算其应力时，修正系数可取1.5～2.5。

2）为了更加准确反映箱梁截面实际裂缝开展情况，对“公路钢筋混凝土及预应力混凝土桥涵设计规范”中正常使用极限状态下的最大裂缝宽度计算公式进行参数修正，取修正系数C3=1.25。

3）根据裂缝宽度比（W1/Wfk）与截面承载率（M1/Mu）之间函数关系，得到了对结构承载潜力和安全性进行初步评估的计算公式，这对定量分析开裂桥梁的受力状态有一定指导作用。