粗骨料膏体低温流变性能及回归模型

尹升华，刘家明，陈威，邵亚建，吴立波，王筱添

（1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京，100083；2.北京科技大学土木与资源工程学院，北京，100083）

近年来，伴随着国家对保护环境要求和采矿行业对经济的追求，催生了一种经济、高效和环保的充填采矿技术即膏体充填。膏体是一种塌落度为18~25 cm、粒级小于20 μm 的颗粒质量分数超过15%、屈服应力在200 Pa 以下时泌水率为5%的牙膏状浆体[1]。粗骨料膏体则是一种以全尾砂为主要集料，根据需求添加废石、戈壁集料、河沙和炉渣等材料复合而成一种非牛顿流体[2-3]。充填膏体一般通过管道输送方式填充地下采空区，因此，新鲜膏体应具备足够的流动性和可输送性。为评价膏体管道输送可行性及可靠性，国内外学者对充填膏体流变性能开展了大量研究。刘泉声等[4]得出在水泥浆温度和水化时间耦合作用下，对于水灰比分别为0.5 和0.7 的料浆，剪切力随着温度升高而增大，而对于水灰比分别为1.0，1.5 和2.0 的料浆，剪切力随着温度降低而减小；PETIT等[5]分析了时间和温度对流动砂浆流变性能综合影响，认为砂浆屈服应力及塑性黏度在时间和温度耦合作用下呈线性变化；薛振林等[6]分析了浆料质量分数（74%，76%，78%和80%），温度（30，40，50和60 ℃）和灰砂比（0.100，0.125，0.167及0.250）对流变参数的影响规律，认为料浆屈服应力影响权重由高到低依次为质量分数、温度和灰砂比。WU 等[7]在水泥水化过程及温度耦合作用下，建立了膏体充填流变特性数学模型，发现膏体预测流变特性与实测流变特性具有较好的一致性。水泥水化温度及水化过程对水泥流变特性和流动性具有重要影响。

充填膏体从制备站到待充采空区输送过程中会遇到各种各样的能量转换以及热量交替，如管道内壁与膏体之间的摩擦，部分动能转化为热能。在长距离输送过程中，充填膏体水化反应释放不可忽视的热量等[8-9]。MAHLABA等[10-11]研究充填膏体流变特性时只考虑了单因素如水泥掺量、剪切时间、质量分数、矿渣和粉煤灰掺量，常常忽略温度、静置时间和配比等多因素对膏体流变性能的影响。北方冬季室外温度低至0 ℃时，会增大输送管道堵塞风险；膏体停泵重启时，膏体静置时间过长会造成膏体管道泵压过大，诱发管道喷浆事故以及因配比不同造成无法输送等其他问题。因此，研究充填膏体在温度（低温）、静置时间和配比对流变特性（屈服应力以及黏度等等）的影响就显得至关重要[12-13]。

本文以金川某矿为研究背景，采用全尾砂、废石和棒磨砂为充填物料，首先，研究物料理化性质，全面了解充填料物理化学特性；其次，运用BROOKFIELD R/S plus 型流变仪、TC-550 制冷型循环浴槽等实验仪器，对全尾砂粗骨料膏体进行流变模型分析，并探究温度、静置时间和尾骨比（全尾砂与废石、棒磨砂质量之比）对膏体流变特性的影响；最后，提出各因素耦合作用下膏体流变特性的回归模型，预测膏体流变特性影响规律，为膏体管道输送提供理论依据。

1 实验

1.1 实验材料

膏体流变特性测试实验材料包括全尾砂、废石、棒磨砂和水泥。全尾砂取自金川选矿厂浓密后泵池；废石及棒磨砂取自二矿区充填粗骨料仓；水泥为PC32.5R型普通硅酸盐水泥，来自市售。充填料物理性质如表1 所示，由表1 可知：全尾砂、废石和棒磨砂相对密度相近，水泥相对密度与市售所给参考值相同；全尾砂孔隙率大于废石和棒磨砂孔隙率。采用X线荧光光谱实验（XRF）分析充填物料主要化学成分，结果如表2 所示，由表2可知：全尾砂主要成分为SiO2，MgO 和Fe2O3，废石主要成分为SiO2，CaO 和MgO，棒磨砂主要成分为SiO2，Al2O3和CaO。

表1 充填料物理性质Table 1 Physical properties of filling materials

利用LMS-30型激光粒度分析仪分析全尾砂粒度，利用人工标准筛分析废石和棒磨砂粒度[14]，其结果如图1所示。由图1可知：全尾砂主要为粒径小于100 μm颗粒；不均匀系数为0.087，曲率系数为1.237；其中0.074 mm以下粒径占80%，属于均匀细骨料。废石主要粒径为4~15 mm；不均匀系数为25.038，曲率系数为7.727。棒磨砂主要粒径为0.45~6.00 mm；不均匀系数为2.073，曲率系数为0.366。综合分析可知，充填料整体级配良好，有利于料浆制备，可用于井下充填。

图1 各物料粒径分布Fig.1 Particle size distribution of each material

表2 物料主要化学成分（质量分数）Table 2 Main chemical constituents of materials（mass fraction）%

1.2 实验方案

为全面分析温度、尾骨比以及静置时间对膏体流变特性的影响，实验分为2个阶段。阶段1选取质量分数（79%）、灰砂比（1：6），静置时间（0 min）、温度（1，5，9，13，17 及21 ℃）和尾骨比（8.0：1.0：1.0，7.0：1.5：1.5，6.0：2.0：2.0 及5.0：2.5：2.5）作为实验因素与水平，探究温度与尾骨比对膏体流变特性的影响。阶段2选取质量分数（79%）、灰砂比（1：6），尾骨比（6.0：2.0：2.0）、温度（1，5，9，13，17 及21 ℃）和静置时间（15，30，60，90及120 min）作为实验因素与水平，研究温度与静置时间耦合下对膏体流变特性的影响[15-16]。具体实验设计方案如表3所示。

1.3 实验设备与方法

实验测试采用TC-550 制冷/加热型循环浴槽（-20~100 ℃）；BROOKFIELD R/S plus 型流变仪，配备规格v40-20的桨式转子（桨叶直径D为20 mm，高度H 为40 mm）。实验时，将物料配制成400 mL膏体料浆置于温控杯内（上覆保鲜膜防止料浆内水分挥发及空气进入）；待膏体到达设定温度，再对膏体进行流变测试实验，测试程序采用控制剪切速率法（CSR），即先保持恒定剪切速率220 s-1进行2 min（确保膏体达到应力松弛状态），再以0.1 s-1剪切速率逐渐递减至0 s-1，整个实验过程持续220 s。

2 全尾砂粗骨料膏体流变模型

目前，描述膏体流变行为模型主要有宾汉体（Bingham）模型、H-B（Herchel-Bulkley）模型、幂律（Power-law）模型以及Ostwald 模型[17]。为探究全尾砂-粗骨料膏体流变模型，图2 所示为在质量分数为79%、灰砂比为1：6、尾骨比为6.0：2.0：2.0（矿山常用配比）下，不同温度和尾骨比下的剪切应力曲线。

由图2（a）可知：在尾骨比为6.0：2.0：2.0条件下，全尾砂粗骨料膏体剪切应力随着剪切速率增加而增加，且上升斜率越来越大；在相同剪切速率下，膏体剪切应力随温度升高逐渐减小。由图2（b）可知：在温度9 ℃（接近北方冬季井下输送管道温度）条件下，全尾砂粗骨料膏体剪切应力随尾骨比增大而增大，即随尾砂质量分数增多，剪切应力逐渐增大。

综上分析可知，在不同温度和尾骨比条件下，其全尾砂粗骨料膏体剪切应力与剪切速率之比（斜率）随剪切速率增加而增大，即不符合宾汉体模型，而符合H-B模型。因此，对温度1，5，9，13，17和27 ℃进行H-B模型拟合，其结果分别如图3和表4所示。由图3 及表4 可知：在尾骨比为6.0：2.0：2.0条件下，H-B模型拟合曲线的R2都在0.99以上，拟合效果显著，且流动指数都大于1，即全尾砂粗骨料膏体属于H-B 模型中膨胀体。这是因为膏体流变特性会随水泥质量分数增加，浆体由宾汉姆流体逐渐转变为膨胀体，且在灰砂比1：6~1：4条件下，膏体呈现剪切增稠特性（膨胀体）[18]。由于本实验所配灰砂比为1：6，因此，全尾砂-粗骨料膏体呈屈服膨胀体，其模型见式（1）[19]。

表3 膏体流变特性实验方案Table 3 Test scheme of rheological properties of cemented paste backfill

图2 不同温度及尾骨比下剪切应力Fig.2 Shear stress at different temperatures and tailings-aggregate ratios

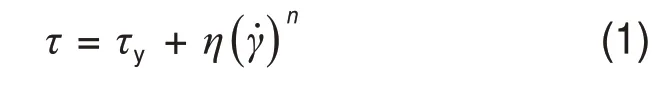
式中：τ为剪切应力，Pa；τy为屈服应力，Pa；η为H-B 黏度，Pa·s；γ˙为剪切速率，s-1；n 为流动指数，n>1表明全尾砂-粗骨料膏体为屈服膨胀体，n<1表明全尾砂-粗骨料膏体为屈服假塑性体。

图3 不同温度下H-B流变模型拟合曲线图Fig.3 H-B rheological model fitting curve at different temperatures

表4 不同温度下H-B流变模型拟合分析Table 4 Fitting analysis of H-B rheological model at different temperatures

3 全尾砂粗骨料膏体的流变特性影响因素

根据H-B模型，探究温度（低温）与尾骨比对HB 模型中屈服应力、H-B 黏度和流动指数的影响。图4所示为不同温度和尾骨比下，屈服应力、H-B黏度和流动指数曲线。

由图4（a）可见：当尾骨比分别为6.0：2.0：2.0 和5.0：2.5：2.5 时，温度1~21 ℃均可进行现场充填作业；当尾骨比分别为8.0：1.0：1.0 和7.0：1.5：1.5 时，5 ℃以上才可以进行现场充填工作。因此，需要尽可能控制充填用水在5 ℃以上。此外，在质量分数为79%、灰砂比为1：6和相同尾骨比下，屈服应力随温度升高呈负指数下降。这是因为当温度从1 ℃升至21 ℃时，膏体内部絮团及絮网间稳定结构被破坏，释放出一定量自由水，导致料浆流动性增强，屈服应力随之降低[20]。屈服应力下降斜率越来越小，是因为温度对水泥水化速率及水化过程也有一定影响，水泥水化速率及水化过程在固定温度内存在最佳状态，因此，屈服应力在1~21 ℃时，曲线下降斜率不尽相同[21]。在相同温度下，随着尾骨比中尾砂质量分数增多，其屈服应力越来越大，可见尾砂质量分数是影响屈服应力主要因素。这是因为金川全尾砂属于极细尾砂，当尾骨比中全尾砂含量增多时，膏体中细颗粒越多，其料浆比表面积越大。因此，需要更多自由水以包裹和湿润细颗粒。

由图4（b）可见：当尾骨比分别为5.0：2.5：2.5 和6.0：2.0：2.0 时，H-B 黏度随温度升高而逐渐降低；当尾骨比分别为7.0：1.5：1.5 和8.0：1.0：1.0 时，H-B黏度随温度升高先上升后下降，说明H-B 黏度随温度变化规律受尾骨比影响。此外，在相同温度下，随着尾骨比中尾砂质量分数增多，其H-B 黏度逐渐增大，且尾骨比增加速率比温度增加速率要大，即尾骨比对H-B黏度的影响大于温度对H-B黏度的影响。

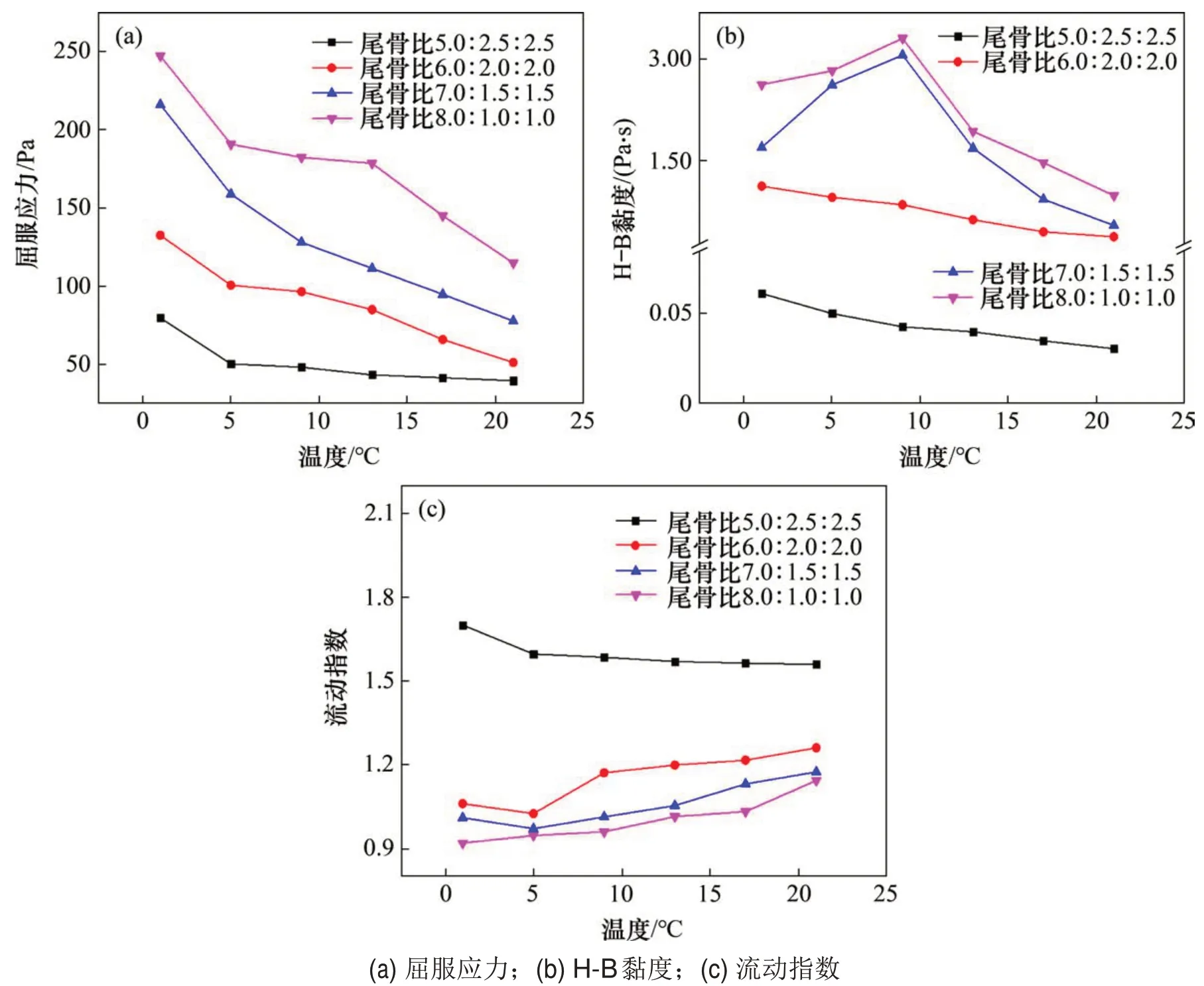
图4 不同温度下不同粗骨料的H-B模型流变参数Fig.4 Rheological parameters of H-B model with different temperatures and coarse aggregates

由图4（c）可见：当尾骨比分别为6.0：2.0：2.0，7.0：1.5：1.5 和8.0：1.0：1.0 时，随着温度的升高，流动指数整体呈增加趋势；当尾骨比在5.0：2.5：2.5时，流动指数随温度升高而减小；在尾骨比分别为7.0：1.5：1.5 和8.0：1.0：1.0 条件下，当温度为1~9 ℃时，流动指数小于1，当温度在10~21 ℃时，流动指数大于1。说明随着温度升高，膏体由H-B模型屈服假塑性体转变为宾汉姆流体再转为H-B模型屈服膨胀体。

4 静置时间对全尾砂粗骨料膏体流变特性的影响

图5 所示为在质量分数为79%、尾骨比为6.0：2.0：2.0 时，不同静置时间（15，30，60，90 和120 min）与温度下屈服应力、H-B黏度、流动指数曲线图。由图5可知：在尾骨比6.0：2.0：2.0条件下，屈服应力随着静置时间呈二次函数增加；H-B黏度随着静置时间呈线性函数增加。这是因为水泥水化硬化作用随膏体静置时间不断增强；絮网结构逐渐发育，水化产物将全尾砂、废石和棒磨砂颗粒紧密连接，浆体内部抵抗外界扰动能力增强，因此，屈服应力与H-B黏度也逐渐提高。

由图5（a）可知：在尾骨比为6.0：2.0：2.0 和相同静置时间下，屈服应力随温度升高而降低，且下降幅度逐渐缩小。说明在静置时间与温度耦合作用下，静置时间不影响温度与屈服应力之间负指数关系。由图5（b）可知，在温度为1 ℃，静置时间由15 min上升至120 min时，H-B黏度增加0.001 5 Pa·s；在静置时间为15 min，温度由1 ℃上升至21 ℃时，H-B黏度增加0.176 8 Pa·s。说明温度对H-B 黏度影响大于静置时间对H-B 黏度的影响。由图6（c）可知：在尾骨比6.0：2.0：2.0条件下，流动指数随静置时间延长基本不增加，这说明不同静置时间对流动指数影响不大；在相同静置时间下，流动指数随温度升高而缓慢上升，且在1~21 ℃时，流动指数都大于1，即膏体都处于屈服膨胀体状态。

图5 不同静置时间的流变特性参数Fig.5 Rheological characteristic parameters with different standing time

5 膏体流变参数回归模型

由图5可知：屈服应力随温度升高呈负指数函数下降；当骨料比1.0≤φ≤1.5时（尾骨比换算成尾骨料比φ，如表5所示），H-B黏度随温度升高呈线性函数下降；当骨料比1.5<φ≤4.0 时，H-B 黏度与温度呈二次增函数关系。流动指数与温度呈线性减函数关系（骨料比φ=1）；当骨料比1.0<φ≤4.0时，流动指数与温度呈线性增函数关系。在相同尾骨比下，某一温度屈服应力、H-B黏度和流动指数都可以通过函数平移或斜移得到其他尾骨比点。根据膏体各流变参数随温度变化特征，屈服应力、H-B黏度和流动指数可用式（2）~（4）表示[22]。

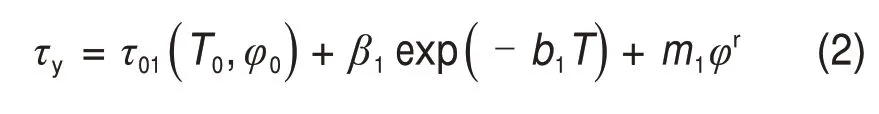
表5 尾骨比与骨料比换算Table 5 Calculation between tailing aggregate ratio and fine-coarse aggregate ratio

式中：T为温度；T0为21 ℃；φ0为1；τ01，η01和n01分别为T0和φ0时刻的屈服应力、H-B黏度和流动指数；其余为待定参数。

由图6可知：当固定温度时，屈服应力随静置时间呈二次函数变化，H-B黏度和流动指数随静置时间呈线性函数变化。在同一温度下，流动参数均可以通过平移或斜移得到其他温度点。根据膏体各流变参数随静置时间的变化特征，静置时间t和温度T时刻屈服应力、H-B黏度和流动指数可用式（5）~（7）表示。

式中：t为静置时间；t0为0 min；τ02，η02和n02分别为T0和t0时刻的屈服应力、H-B黏度和流动指数。

将式（2），（3）和（4）分别代入式（5），（6）和（7），得到关于温度T、骨料比φ 和静置时间t 关于屈服应力、H-B 黏度和流动指数回归模型，如式（8）~（10）所示。

式中：τ03，η03和n03分别为T0，t0和φ0时刻的屈服应力、H-B黏度和流动指数。

采用式（8）~（9）对实验数据进行拟合，得出模型中待定系数，其函数见式（11）~（13），对其进行假设检验、系数检验和统计分析，结果见表6。由表6可知：回归模型拟合效果显著。影响屈服应力顺序由大到小依次为骨料比、温度和静置时间。影响H-B 黏度（η）和流动指数顺序由大到小依次为骨料比、温度和静置时间。

表6 各计算模型统计分析Table 6 Statistical analysis of each calculation model

6 结论

1）全尾砂粗骨料膏体符合H-B 模型；在相同剪切速率下，剪切应力随温度升高而减小，随尾骨比值增大而增加，随静置时间延长而增加。

2）屈服应力随温度升高呈负指数函数下降，随静置时间呈二次函数上升，随尾骨比增大而增加。H-B 黏度随静置时间延长和尾骨比增大而增加，随温度的变化受尾骨比影响，当尾骨比分别为5.0：2.5：2.5 和6.0：2.0：2.0 时，H-B 黏度随温度升高而逐渐降低，当尾骨比分别为7.0：1.5：1.5 和8.0：1.0：1.0时，H-B黏度随温度升高先上升后下降。温度、尾骨比和静置时间对流动指数影响不大。

3）影响屈服应力、H-B黏度和流动指数顺序由大到小依次为骨料比、温度和静置时间。在尾骨比分别为7.0：1.5：1.5 和8.0：1.0：1.0 时，随着温度升高，膏体先由屈服假塑性体转变为宾汉姆流体再转变为型屈服膨胀体。

4）建立了关于骨料比、温度和静置时间的流变特性回归模型，拟合效果较好。