利用Halo轨道仿真开展嫦娥四号中继星与月面设备干涉基线的研究*

武宇翔，温卫斌，平劲松，朱新颖，张洪波，孔德庆，戴 舜，薛喜平，李 臣

(1. 中国科学院国家天文台，北京 100101；2. 中国科学院月球与深空探测重点实验室，北京 100101；3. 中国科学院大学，北京 100049)

1 Halo轨道和中继卫星

我国的嫦娥工程已经进行了多次任务，嫦娥四号探测器首次实现了月球背面着陆探测。由于月球背面的着陆器无法与地面直接进行通信，为了建立着陆器、巡视器与地球之间的联系，我国发射了中继通讯卫星 “鹊桥号”，通过它把获得的科学数据传回地球。这颗中继星运行在地月拉格朗日点L2附近的使命轨道上[1-4]。中继通信卫星搭载的低频射电探测仪和月球着陆器上搭载的射电频谱仪为空间低频射电干涉测量创造了条件[5]。

月球背面屏蔽了来自地球的各种信号，给低频射电观测提供了宁静的环境，可以在0.1～40 MHz的频段开展低频射电天文观测[6]。由于低频射电波的波长较长，为达到较高的空间分辨率，可参照甚长基线干涉测量(Very Long Baseline Interferometry, VLBI)技术，借助月面、中继星和地面的低频射电观测设备联合进行协同观测，甚至是干涉测量。为了考察这种空间干涉测量的可行性，我们建立理论和仿真模型进行模拟实验，其中的一个重点是模拟中继星到月面设备的基线并计算基线长度。为此，本文讨论了Halo轨道模型在空间低频射电干涉测量模拟中的适用性。

嫦娥四号任务选择南极-艾特肯盆地(Southpole-Atiken)作为着陆区，着陆器及巡视器在这一地区开展科学探测，并获得了有关月幔物质的探测数据[7]。通过开展形貌分析、物质组成、月壤和月表浅层结构的综合探测，有望获得诸多有关月球形成的新证据[8]。2018年5月21日，中继通信卫星 “鹊桥号” 成功发射，进入地月L2点附近的使命轨道，其中，L2点是指限制性三体问题(Restricted Three Body Problem, RTBP)的5个特解，被称作拉格朗日平动点中位于较小大天体外侧的共线点，文[9]进行过系统性的总结。利用地月L2点附近轨道部署中继卫星开展月球背面的探索这一构想由文[10]提出，文[11-12]研究丰富了平动点轨道力学的理论体系，文[13-15]给出了Halo轨道的三阶近似解析解，广泛应用于三体问题，在文[16]提出在平动点建立空间站的设想之后，文[17]提出了中继通信链路和月球采样高速公路。第一次平动点轨道探测是日地L1的ISEE-3，美国的ARTEMIS任务首先进行了地月平动点的验证飞行；嫦娥二号探访了日地L2点的Lissajous轨道；嫦娥5T1月球再入返回试验任务进入了地月L2点Lissajous轨道；嫦娥四号中继星则使用地月L2点附近的Halo轨道[18-19]，国内也有多项与中继星使命轨道相关的建模仿真以及实际测量研究[20-21]。

为了开展空间低频射电干涉测量系统的相关研究，本文构建了地月L2点附近的Halo轨道，并比较模型与中继星实际使用的理论轨道之间的关系，对模型与理论轨道的偏差进行了比较，并分析了模型对星上设备与月面设备形成基线长度的影响，评价模型的仿真效果。

2 平动点轨道的相关理论

限制性三体问题描述了一个质量小的物体在两个大天体附近空间受万有引力作用的情况，在特殊情况下，小物体受到来自大天体的引力能满足自身向心加速度所需，从而稳定运行。这种稳定平动的5个特解被称为 “拉格朗日平动点”，其中，L2点是位于两个大天体连线上、较小的天体外侧的平动点，在这一点上可以找到一些轨道使得小物体能以较低的能耗、较长的时间维持在稳定的位置。然而L2点并不是一个稳定点，所以这类轨道都不是完美的周期轨道，依然需要时常进行轨道维持机动，常见的L2点轨道有Lyapunov轨道、Lissajous轨道和Halo轨道。

在地月系空间定义一个右手直角坐标系，并称之为旋转坐标系(Rotation System)，它的原点始终是地月连线的瞬时平动点L2，x轴方向与地球指向月球的方向相同，z轴与地月之间的旋转角速度方向相同。在这个坐标系内，Lissajous轨道和Halo轨道的运动都可以描述为 “Az=0” 的平面内与平面外的两种振动的叠加。平动点轨道的一般表达式为

(1)

其中，Ay和Az分别为旋转坐标系下面内和面外振幅；λ为面内振动频率；ν为垂直于面的振动频率；φ和ψ分别为面内外振动的初始相位。

一种Lissajous轨道的示例如图1(a)，这种轨道在地月旋转面内周期与面外周期并不相同，所以轨道呈现Lissajous曲线的形式，卫星在经过中央位置时，有可能被月球遮挡，不能建立对地球的联系。而Halo轨道(如图1(b))的尺寸较大，且面内周期与面外周期相同，它不会被遮挡，能够保证在全程保持同时对月背和地球的直视，保证地面-中继星-月球背面的通讯连续性。Halo轨道的表达式为

(2)

此时，面内振动和面外振动的频率相等且为λ。描述Halo轨道的尺寸一般用Ax和Az两个参数，分别是面内振幅和面外振幅。Halo轨道实际上是一个集合，被称为轨道族(Family)，因此，对Halo轨道的模拟还需要进一步简化，并且Halo轨道的稳定性有限，随着时间的变化，航天器会逐渐偏离标称轨道(Standard Orbit)。文[12]给出了一个用准周期(Quasi-periodic)轨道描述Halo轨道的数值构造方法，这种方法计算量较小，且能够较好地描述Halo轨道的特征。它的基本形式是

(3)

各参数意义见文[12]。在描述振幅时，也可以用y方向的面内振幅Ay与面外振幅Az两个参数。为了保证面内与面外的频率相等，Ay和Az应该有以下关系[12]：

(4)

利用这个关系式可以得到Ay的最小值是46 793 km，由此可以得到Halo轨道的一般表达式与Az之间的关系。

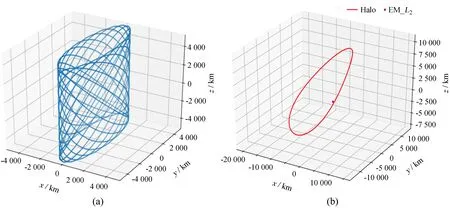
图1(a)Lissajous轨道和(b)Halo轨道示例Fig.1 Examples of (a) Lissajous orbit and (b) Halo orbit

3 利用中继星轨道的验证实验

为检验Halo轨道模型，选取嫦娥四号中继星 “鹊桥号” 于2019年12月22日0时0分0秒到12月23日23时59分59秒实际使用的理论轨道[19](以下简称实际轨道)，每个数据点的间隔为1 s。实际轨道数据包含北京时间、地心坐标系统下中继星的位置坐标(km)以及速度矢量(km/s)。根据嫦娥四号中继星所在使命轨道的相关参数，调整模型内的面外振幅Az和初始相位θ，使得模型与实际轨道匹配[20-21]。对Halo轨道的模拟实际上是对使命轨道的标称轨道进行模拟，卫星进行多次轨道机动(Orbit Maneuver)以确保卫星不远离标称轨道，但综合考虑轨道稳定性，并节省推进剂以延长任务寿命，实际轨道与标称轨道也有所差别。

为了清晰地表现轨道的特征，选择旋转坐标系对实际轨道数据和模型数据进行对比。首先将实际轨道的时间系统和空间坐标系进行转换，将时间统一到地球时(Terrestrial Time, TT)，能够兼顾地球附近时间和行星历表的精度要求[22]。在进行空间坐标系转换时选用喷气推进实验室(Jet Propulsion Laboratory, JPL)的DE430行星历表。

首先，将时间统一到地球时。由于中继星轨道处于地月附近的空间，为获取相应时刻的行星历表数据，应当采用地球时代替历书时读取历表，在保证精度的前提下统一模型和实际轨道数据的时间基准。首先将北京时间转换到格林尼治时间的协调世界时，然后使用国际地球自转服务(International Earth Rotation Service, IERS)发布的地球指向参数(Earth Orientation Parameters, EOP)将协调世界时转换到UT1时间，计算跳秒(Leap Seconds)后将时间转换到地球时即可。图2是这一过程的示意图。

图2 时间系统转换Fig.2 Transforming of time system

通过地面深空站测距、测速和VLBI测量数据估算和预报中继星实际轨道的位置和速度，这种信息采用的参考系应为地心地固坐标系。若要使用实际的测量数据，应该将这种坐标转化到合适的空间坐标系。地心地固坐标系包含地球自转、章动岁差等因素，且这些因素与月球附近卫星运动以及月球本身的天平动无关。在地心地固坐标系中描述中继卫星平台和月面着陆器平台的运动规律复杂且不能体现特征，需要将其转换到合适的坐标系。为了呈现Halo轨道的主要特征(近似于一个竖立的圆环)，应将轨道数据转换到旋转坐标系中，直观地对轨道数据和模型进行比较。

坐标转换的流程如图3，地固坐标系是原点位于地球质心，且固结于地球，随地球一同运动的坐标系。首先将地心坐标系转换到国际地球参考系(International Terrestrial Reference System, ITRS)；再利用国际地球自转服务发布的地球指向参数数据，调整极移、地球自转角和章动-岁差，将坐标转换到地心天球参考系(Geocentric Celestial Reference System, GCRS)以及国际天球参考系(International Celestial Reference System, ICRS)。

图3 空间坐标系统转换Fig.3 Transforming of reference system

下一步将坐标转换到旋转坐标系。由于旋转坐标系与地月有关，首先得到某时刻地球和月球的质心，由两者连线得到旋转坐标系的x轴，月球围绕地球公转的角速度方向即为z轴，根据右手螺旋法则可以得到y轴的方向，由此可以将国际天球参考系下中继星的位置转换到旋转坐标系，转化结果如图4。图4中，蓝色粗线是实际轨道数据，从12月22日0时至12月23日24时中继星在旋转坐标系中的轨迹，称为观测数据(图中 “O”)；红色细线是与这段时间的实际轨道对应的Halo轨道模型在一个整周期内的轨迹，称为计算数据(图中 “C”)。由图4可以看出在这段时间内，实际轨道与Halo轨道模型符合较好。实际数据与Halo轨道模型重合的部分做差，并对差值取模，可以得到图5。

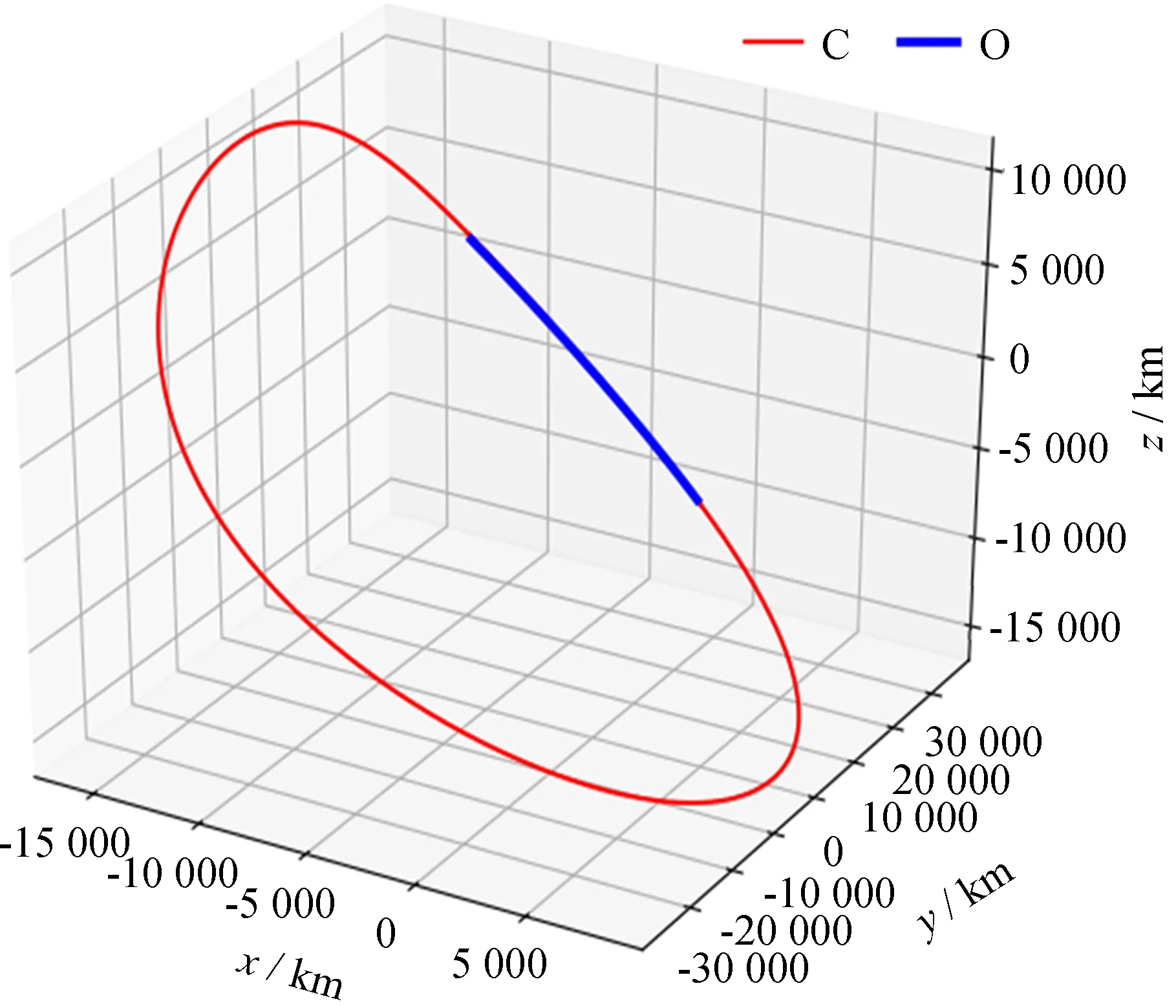
图4 Halo轨道模型与部分中继星轨迹Fig.4 Halo model and part of relay satellite orbit

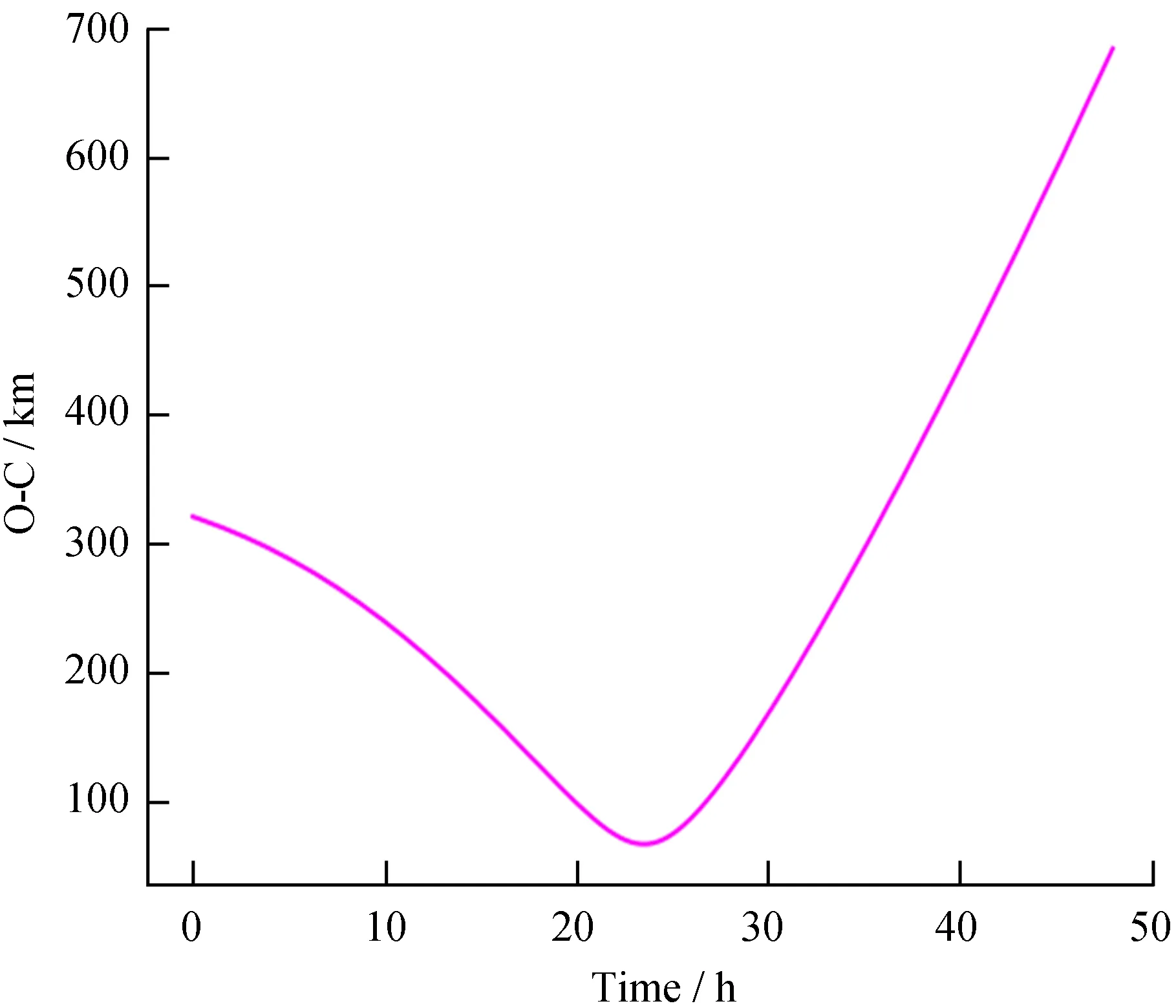
图5 观测轨道与模型轨道的差Fig.5 Differences between observation and model orbits

从图5可以看到，这段数据总体符合较好，总的误差值不超过700 km，说明模型参数与实际情况接近。但观测数据和模型数据之差在中段的变化趋势发生了变化，说明实际轨道有更加复杂的运动形式没有被模型完全描述。

这里的Halo轨道模型将应用于空间射电干涉测量的研究，所以需要考察模型与理论轨道在干涉测量中的差别。首先考察中继星与月面设备干涉时形成的基线。基线是指干涉测量中两个天线单元之间的距离，随着基线的变化，两个天线单元对同一目标的观测信号能够形成干涉，为了顺利开展干涉测量，需要基线的长度以及基线与目标源的方向。

如果在月球背面位于地月连线上的一点有一个低频探测设备，它与中继卫星上的低频探测设备进行干涉测量，那么它们之间的基线是从月面设备指向中继卫星的向量，长度就是这个向量的模。利用观测数据和模型数据可以分别求出这段时间内的基线及长度，基线长度随着时间的变化如图6。图6是从2019年12月22日开始，基于观测数据和模型数据分别计算基线长度随时间变化的情况。其中横坐标是从12月22日0时起经过的时间(单位：小时)，纵坐标是此时刻基线的长度；蓝色线条代表观测数据得到的基线长度，红色线条代表模型数据得到的基线长度。总体来说它们的变化趋势一致，为了比较两者的差异，对两条基线长度做差得到观测数据和模型数据的基线长度之差随时间的变化关系如图7，从图7可以看到，两种情况下基线长度的差距不大，普遍在几十千米范围内。甚长基线干涉测量的相关处理需要时延的误差在一定范围内，时延误差的重要组成部分是几何时延误差，即对基线长度的计算应与真实值尽可能一致。相关处理对时延误差的要求可以描述为[22]

(5)

其中，N为谱通道个数；B为带宽。如果以嫦娥四号着陆器低频射电频谱仪的相关性能参数为参照，进行甚长基线干涉测量相关处理需要的时延误差应低于0.819 ms，对应的基线长度误差应低于245 km。几何时延虽然是总时延的主要部分，其他的因素(如传播介质造成的时延)也会对最终时延的估计产生影响，所以，基线长度估计误差造成的时延估计误差应该小于上述计算值。如图7，随着卫星继续运行，它的轨道逐渐回到标称轨道附近，后半段的差值最大只有50.94 km，平均值30.00 km，可以认为在这一阶段，模型对实际轨道的符合效果较好。

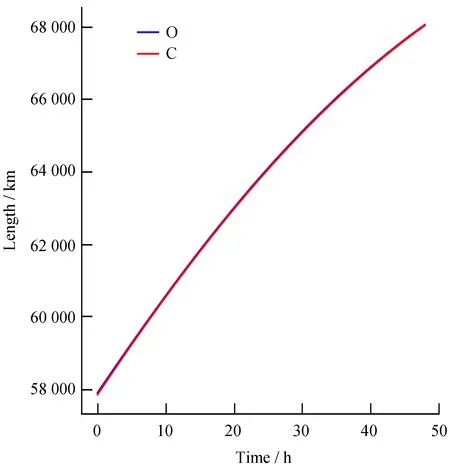
图6 观测基线与模型基线长度Fig.6 Baseline lengths of observation and calculation

图7 两种基线长度之差Fig.7 Differences of baseline lengths

4 讨论和展望

数据显示模型与中继卫星的理论轨道之间存在一定的差距，可能的原因有两个：(1)出于计算简便的考虑，这个模型实际上是为了特定的目的，利用一个周期化的Halo轨道代替实际的使命轨道，在满足问题探究需求的前提下，Halo轨道模型与理论轨道之间存在较小的差异；(2)中继卫星实际运行的使命轨道并非Halo轨道族，而是以理论轨道为标称轨道设计的运行轨道，在保证位置稳定且符合功能需求的同时，尽可能降低推进剂消耗，延长任务寿命，同时易于进行轨道维持控制。这两个因素会显著影响模型与实际轨道的符合程度。

本文采用一个准周期的Halo轨道模型，与嫦娥四号中继卫星 “鹊桥号” 的理论轨道数据进行了比对，两者与月面着陆器形成的基线长度的差异较小，两种基线长度差平均值为30.00 km。

在高频频带，干涉测量拟采用条纹搜索方法，对基线精度需求是波长的数千倍，即百千米左右，可以认为这种模型基本满足空间低频射电干涉模拟实验的要求。在空间低频射电干涉测量得以实施之前，可以通过建立模型、数值模拟的方法对干涉测量系统的组成、方法和性能进行计算和预测，计算结果将为实施空间低频射电干涉测量提供参考。