基于节点重要性和局部扩展的重叠社区发现算法*

郭 峰 尤凯丽 李昕泽

（北方工业大学信息学院 北京 100000）

1 引言

社区发现是复杂网络［1～3］及数据挖掘领域中关键的研究内容。社区结构［4～6］作为复杂网络的共同特征，是网络图中最普遍、最重要的属性之一，表现在社区内部节点之间的连接要比社区外其他部分节点的连接要更加紧密［5］。通过社区发现可以帮助我们了解和分析病毒传播行为，有助于推断病毒的传播机制，从而快速地采取有效防范、制定应对措施。社区发现问题具有重要的研究价值和科学意义，近年来，如何对社区结构进行快速、准确地划分成为众多学者研究的热点。

社区结构具有一些明显的属性和特征［7］，使得在重叠社区划分方法上出现不同的优秀思想。2002年，Girvan和Newman基于分裂思想提出经典的GN算法［8］，为复杂网络研究开辟了新的道路；2005年，Palla等对原有非重叠社区发现方法进行扩展，首次提出基于派系过滤思想的重叠社区发现算法CPM［9］。随后，各种重叠社区发现思想层出不穷，典型算法有围绕CPM算法中寻找相邻k阶完全子图的核心思想，Farkas等提出对加权网络的社区划分算法CPMm［10］、Kumpula等提出快速的派系过滤算法SCP［11］等。2007年Raghavan首次运用标签传播思想对图进行划分，提出著名的非重叠社区发现算法LPA［12］。其后，在LPA算法基础上，Steve等引入多标签和隶属度概念提出重叠社区发现算法COPRA［13］；Xie等引入Listener和Speaker概念提出SLPA算法［14］；Xie等结合派系相似度，以派系为载体进行标签传播，提出CSLPA算法［15］等。

局部扩展方法是重叠社区发现任务中比较常用且成功的策略之一。Lancichinetti等提出的LFM算法［16］是局部扩展思想中的一个典型算法，但该算法受参数影响及初始节点的随机选择，导致检测精度不稳定，算法不具有鲁棒性。Shen等引入树状图概念提出EAGLE算法［17］，还提出了一种评估重叠社区的模块化度量EQ；与EAGLE算法思想相同的还有Huang等提出的DenShrik算法［18］和Lee等提出的GCE算法［19］等，但DenShrik与EAGLE类似，需要在检测小规模社区时手动调节阈值，GCE算法对初始节点进行贪婪扩展，并设计函数计算社区之间的距离来删除相似社区，但在人工网络上的表现效果比在大规模密集型网络上表现效果更好。

如何在复杂网络图中准确、快速找出重叠节点和社区、有效地划分社区结构是本文研究的重点。

2 算法

2.1 DocNet

DOCNet算法［20］是2014年Delel Rhouma等提出的基于局部扩展的一种重叠社区发现方法。该算法的主要策略是：找到最重要的节点与其邻节点形成一个初始社区，筛选达到规定质量函数标准的节点加入初始社区，遍历各个节点对初始社区其进行扩展。DOCNet算法发现重叠社区的过程可以总结为两个阶段，即构建初始社区和社区扩展。

1）构建初始社区

DOCNet算法选取最重要的节点及其邻节点组成初始社区，节点重要性随着其邻节点的增加以及这些邻节点之间边数的增加而增加，也就是说，当一个节点成为网络中“有影响力的中心节点”时，其重要性就会增加。节点重要性是度量一个节点是否能够形成初始社区C的重要因素。

文中将节点重要性N I(u)定义为式（1）：

其中cf c(u)代表聚类系数， ||B(u)代表节点u的邻节点数。

2）社区扩展

初始社区形成后，DOCNet算法遍历社区相邻节点，定义节点u对社区C的隶属度来判断选取哪个节点加入到社区C。隶属度di st moy定义如式（2）所示：

其中dist(u，v)代表节点u，v之间的最短距离，即从节点u到节点v的最短路径的边数。

选取出加入社区C的候选节点u后，DOCNet算法通过定义质量函数来判定节点u是否能加入社区C。质量函数通过社区内外部联系来限定一个社区，当加入节点u后的IC(C)比原来的IC(C)大时，则说明u可以加入社区C。计算方式如式（3）所示：

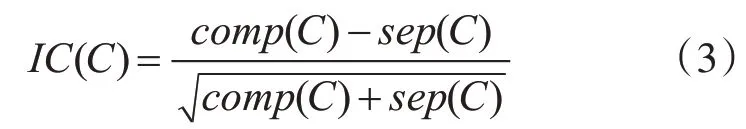
其中comp(C)是社区C内的边数，sep(C)是社区C内节点与社区外节点相连的边数。

DOCNet算法过程简单，在复杂网络以及社区之间的重叠率高的网络上有着很高的稳定性，但仍存在一定的局限性，本文提出DOCLLE（Discover Overlapping Communities by LeaderRank and Local Expansion）算法，在节点重要性和隶属度两个方面对其进行改进。

2.2 DOCLLE

初始节点的选取是局部扩展方法中关键的第一步，对最终的社区划分结果影响很大［21～22］。针对节点重要性的计算，本文采用更优的排序算法LeaderRank对图中各节点进行排序。在扩展过程中，DOCNet算法采用平均距离来计算节点归属度，使得算法运行时间变长，本文结合节点间相似度概念，在局部范围计算节点对社区的隶属度，减小了计算范围，并具有一定的准确性。

2.2.1 节点重要性

LeaderRank重要性排名算法是对PageRank算法的扩展，该算法加入延迟及自适应概率等思想有效地解决了PageRank算法中每个节点的随机跳转概率都相同且最优参数不具有普适性的问题，在标识图中节点重要性上有很好的性能。

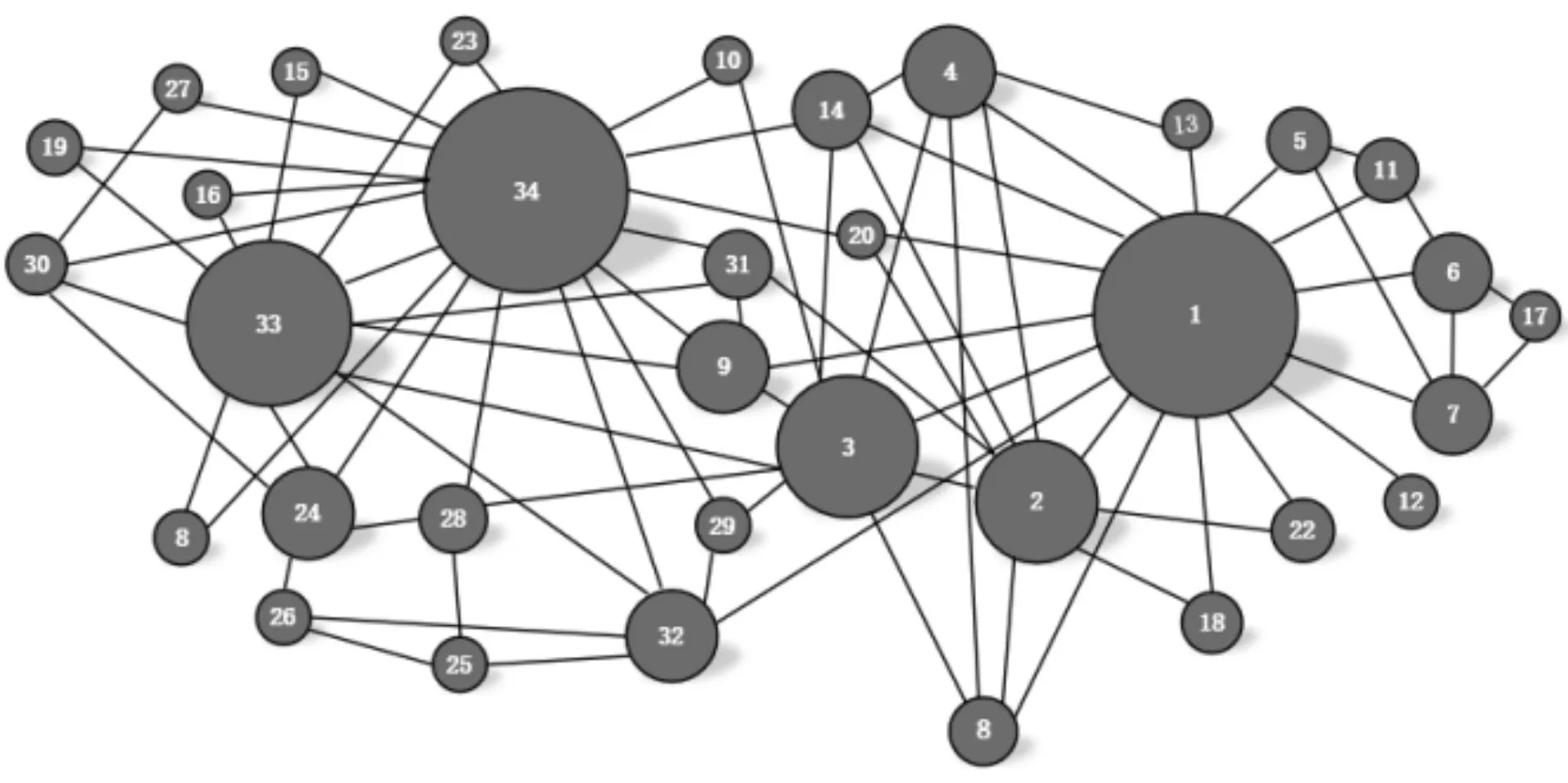
图1 Zachary空手道数据集各节点重要性

在有向图和无向图上应用LeaderRank算法后发现，该算法在两种类型的图上均具有良好的性能，图1所示为LeaderRank算法在无向网络图Zachary空手道俱乐部人员关系图上对各个节点的重要性排序结果。

2.2.2 隶属度

DOCNet算法采用节点到社区各点的平均距离值来衡量节点对该社区的归属度，算法运算过程需要计算两个节点间的最短距离，处理节点数较多的网络图时所需时间较长。文中所提DOCLLE算法采用局部范围内计算节点间的相似度的方式来衡量节点对社区的隶属度，不需要遍历全局节点，提高了运算效率。杰卡德（Jaccard）系数是衡量两个集合之间相似度的指标，常用于比较有限样本集之间的相似性与差异性。集合A、B的交集在两个集合的并集中所占的比例即为杰卡德系数，如式（4）所示，Jaccard系数值越大，样本相似度越高。

节点间相似度可以用杰卡德相似度系数来衡量，为适应图中节点特征，对杰卡德系数进行更改，更改后的杰卡德节点相似度Si m(i)，j如式（5）所示：

节点对社区的隶属度大小与该节点与社区内部各节点之间的关联程度有关。DOCLLE算法在候选节点集中选择加入社区中的节点时，定义了如式（6）中所示的节点隶属度Bl(u，C)：

其中C为每次迭代过程中的初始社区集合，P是C的边界邻节点集合，ω、φ分别是C和P中的节点，e uω为节点u与社区C中节点的连边数，e uφ为节点u与社区P中连边数。

2.3 算法描述

基于局部扩展的核心思想，文中有效地改善了DocNet算法的局限之处。算法主要分为三个步骤：1）通过LeaderRank算法获取图中所有节点的重要性并用LR表示，将LR按重要性大小降序排列并选择第一个节点作为初始节点，与其邻节点共同构成初始社区C；2）对LR进行遍历，通过式（6）依次计算C的边界邻节点对C的隶属度大小，用Bldegree表示，在Bldegree中依次选择隶属度最大的节点加入初始社区C；3）通过式（3）定义的质量函数计算加入新节点后的社区质量，衡量该节点是否可以加入初始社区中；LR中节点全部遍历后，算法终止。

3 实验

3.1 人工生成网络评估

LFR人工生成基准网络能够生成给定参数的网络图，其中混合参数μ代表了每个节点到其社区外部节点之间的连边比例，μ值越大，合成网络中的社区间边数越多，社区内的边数较少，从而使社区结构更难检测。其他参数设置如表1所示。

表1 人工生成网络参数设置

人工生成网络benchmark根据设定的参数生成相应的网络图，社区个数是已知的，这里采用标准化互信息NMI（Normalized Mutual Information）［23］对算法进行检验。NMI的取值范围为0～1，值越大，说明社区发现结果越准确。将DOCLLE与DOCNet算法在以上各组人工生成网络图上进行实验，实验结果如图2所示。

人工生成网络参数的组合设置使得各组网络图规模、复杂度都有所区分，从图2中可以看出，在网络图节点数达到5000时，DocNet算法的NMI值呈下降趋势，在第7，8，9组实验的网络图中的社区划分结果并不好，而DOCLLE算法则呈上升趋势，社区划分能力比较稳定，能够在节点较多的网络中表现出很好的重叠社区发现效果。

图2 DocNet与DOCLLE在人工网络下NMI值对比

图3 DocNet与DOCLLE在GN网络中不同μ值下NMI值对比

为进一步检验DOCLLE算法，另外选择在GN基准网络在不同μ值下的网络图上进行实验，从图3中可看出，μ值大小对算法检测到的社区划分质量有很大的影响。随着μ值增加，NMI减小，这意味在同等节点数的网络规模下，随着网络变得更加复杂，算法计算出的划分结果与真实社区划分情况相差更远。虽然如此，DOCLLE算法在复杂的网络上表现出了比DocNet算法更好的重叠社区划分性能，划分结果更加准确。

3.2 真实网络评估

为检验在真实的重叠网络上DOCLLE算法的效果，文中在Zachary、Dolphins、Footbal、Netscience四个真实数据集进行实验。其社区规模是增大的，Netscience中1589个节点，2742条边。图4展示了DOCLLE算法在Zachary数据集上的社区划分情况，图中的节点表示俱乐部成员，图中的边表示两个成员之间有关联。算法能够识别出重叠节点，将该社团分为两个社区，各包含21个节点，其中绿色节点为两个社区间的重叠节点，以其为边界将Zachary社区结构进行了明确的划分。

图4 DOCLLE在Zachary上的社区划分结果

对真实网络来说，社区个数是未知的，采用以下比较适合衡量社区结构［23］的评价系数：社区连接紧密度指标EQ［17］和模块化指标Qov［24］对算法进行检验。评价系数的取值范围均为（0～1），值越大说明算法效果越好。

将文中提出的DOCLLE算法与局部扩展经典算法LFM［16］、DEMON［25］、标签传播算法SLPA［14］以及DocNet［20］算法进行对比，并在上述四个真实数据集上做对比实验。从图5和图6中可看出，DocNet算法在不同数据集上均有比较好表现，但在规模较大的Netscience数据集上，Qov分值较DOCLLE来说相对较低；DOCLLE算法在不同数据集上均有比较好的表现，尤其在Netscience数据集上，相较于LFM、SLPA、Demon算法来说，DOCLLE算法的EQ值、Qov值是最高的，这意味着随着网络中节点数量的增多，DOCLLE算法的社区划分能力在逐步增强。

图5 各数据集上各个算法的EQ值

图6 各数据集上各个算法的Qov值

3.3 算法时间复杂度

假设图中的节点数为n，边数为m，平均社区规模为c，平均节点度数为d。算法在计算节点重要性的过程中，由于LeaderRank算法迭代次数多，运行时间过长，导致算法复杂度较高。实验中，在保证结果正确的前提下，通过调整终止条件的参数来降低迭代次数，同时对代码进行优化，这里设结果稳定时所需的迭代次数为s，优化后的LeaderRank算法时间复杂度为O（ms）；计算质量函数的时间复杂度为O（cd）；计算隶属度的时间复杂度为O（n2），DOCLLE算法整体的时间复杂度为O（n2cd）。

4 结语

本文在局部扩展算法DocNet的基础上，在初始节点选取和隶属度两个方面做了改进，通过引入经典的重要性排序算法LeaderRank对节点重要性进行排序，得到初始的核心节点；采用局部相似度的计算方式替代DocNet中的平均距离计算方式，以期在处理节点较多的网络时减小计算范围，提高算法效率。实验结果表明，在节点多的网络图上，DOCLLE算法有更好的表现，能够以较高的效率发现重叠社区。在未来工作中，需在真实场景中将算法进行应用和进一步的改进，使算法在处理这些网络图时更具有准确性和普适性。