基于Star CCM+的闸站上游流道方案设计与数值模拟

徐捷，施伟，袁寿其，李彦军，李亚林*

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013；2. 南水北调东线江苏水源有限责任公司，江苏 南京 210029)

泵站是农田灌溉、城市供排水、电厂循环水和大型调水工程的重要组成部分.在泵站工程中，前池对泵站性能具有较大影响.前池设计不合理会导致进水池旋涡较多，理想的前池可以保证水流从引渠流向进水池平顺地扩散，为进水池提供良好的进水条件[1].

在前池流态优化方面，发现导流除涡装置主要为底坎、锥台、导流板、导流墩、导流栅、立柱等[2-3]，国内外对这些装置的不同形状和组合形式进行了大量的模拟和试验研究[4-6]，韩晓维等[7]以流道进口断面流速均匀度和流速加权平均偏流角为进流指标函数，对不同机组组合运行时的进水池内流态及流道进口进流条件进行研究，发现多机组泵站各台泵的运行性能与其所在前池中的位置和其他机组开机台数密切相关.

在进水池的流态方面，颜红勤等[8]发现应尽量避免水泵梁、进水池中有检修平台、胸墙等严重影响流态的建筑物，但并未提出可替代方案；高传昌等[9]为了解决泵站长期低水位运行的问题，采用流体体积(VOF)模型分析了不同水位及开机组合情况下泵站进水池的水流流态.杲东彦等[10]发现在有偏流进水条件下采用蜗形进水池，能够进一步改善前池来流流态；李刚等[11]研究了水泵站与节制闸联合工作的情况，得知闸站之间有相互影响，并对流场进行了优化.

文中在以上国内外文献的基础上，分析影响进水流道内流态的各个因素，包括进口射流水利结构、河道曲率型线；此外，由于节制闸流道处存在较大的死水旋涡，因此对改进导流栅长度、调整进水方式等进行研究；综合上述影响因素，然后以泵各个进水流道内流态均布为目的，得到闸站上游流道设计的规律.

1 数值模拟

1.1 控制方程和湍流模型

泵站运行模式下，流道内水流的流动属于不可压缩湍流流动.湍流流动具有紊动性，选用对三维流动运用最广的标准k-ε模型进行求解.

采用商业软件Star CCM+，利用有限控制体积法对雷诺时均Navier-Stokes方程进行数值离散，数值求解方法采用SIMPLEC算法，求解精度为2阶，一阶残差收敛精度为10-5，二阶残差收敛精度为10-4.

当泵站模式开启后，节制闸流道闸门关闭，上游流道和下游流道通过贯流泵进行流量输运，将闸站全流道进行简化并分别进行研究，计算域如图1所示.

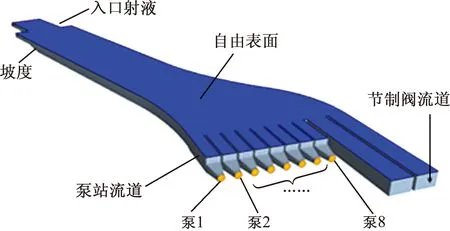
图1 闸站上游流道水力模型Fig.1 Hydraulic model of upstream channel of sluice-pumping station

上游计算流道截止于贯流泵进口，计算域包括进口引渠、前池、进水池.

1.2 边界条件和网格划分

闸站设计最高水位为8.50 m，设计最低水位为7.00 m.选用8台潜水贯流泵作为工作水泵，单泵设计流量为10 m3/s，设计扬程为5.27 m，单泵质量为16 t，轴向水推力为166.2 kN.

泵站运行模式下的边界条件与泵站开启台数以及自由表面的高程有关，故设计上游流道计算域的进口边界条件采用速度进口，速度计算公式为

v=iQd/A，

(1)

式中：i为贯流泵开启台数；Qd为每台贯流泵的设计流量，10 m3/s；A为上游流道进口几何面积，m3.

上游流道计算域出口采用自由出流，河面边界(自由表面)做对称平面处理[12]，即Symmetry边界，并采用自由面刚性假定的方法[13].在河底和两岸以及泵流道进出口边界采用无滑移的固壁条件.

多面体网格对复杂几何结构具有较强的适应能力，并且能有效提高网格的质量和自动化生产网格的效率，因此采用Star CCM+软件对上游流道进行12面体网格划分，划分结果如图2所示.

图2 上游流道多面体网格划分Fig.2 Polyhedral mesh upstream flow channel

为了适应湍流模型的需要，在壁面处加密了2层边界层网格，上游进水流道的网格单元体总数为1 006 101～1 446 772，经验证满足网格无关性要求.

2 优化方案及模拟结果分析

2.1 水力特性评价指标

进水池提供的进水条件、流道的形状，将直接影响泵站水泵进口水流的水力特性，而泵站下游流道受到泵站上游流道的影响尤其是水泵出口的状态影响，因此将通过泵站进口断面轴向流速分布均匀度、泵站出口截面水流偏流角2个方面进一步评价泵站上游流道的合理性.

2.1.1 泵站进口断面轴向流速分布均匀度

泵站轴向流速分布均匀度VZ越接近100%，泵站进口水流的速度分布越均匀，说明流道设计越合理，其计算公式为

(2)

式中：VZ为轴向分布流速均匀度；vai为网格单元i的轴向速度；va为轴向速度平均值；ΔAi为网格单元i的面积；A为泵站进口断面的面积.

2.1.2 泵站出口水流偏流角

泵站出口断面的水流偏流角θ是指泵站出口断面水流轴向流速与实际流速之间的夹角.θ越小 ,出口水流越接近垂直于出口断面，说明流道的设计越合理.出口水流偏流角θ计算公式为

(3)

式中：vti为出口断面各计算单元的横向速度.

2.2 进口射流扩散角的影响

进口射流对整个流道流态的影响较大.前池扩散角是影响前池尺寸和水流流态的主要因素.如果前池扩散角不大于水流的临界扩散角，则水流不会产生脱壁现象，可以避免产生回流[14].

图3为进口射流扩散角影响方案示意图：方案A为原始方案，是一种阶梯式射流结构；方案B为无射流方案，如红色虚线所示；方案C为大扩散角射流方案，即30°扩散角方案，如绿色虚线所示；方案D为小扩散角射流方案，即10°扩散角方案，如紫色虚线所示.4种方案主要对比有无射流结构以及射流扩散角度对泵站流态的影响.

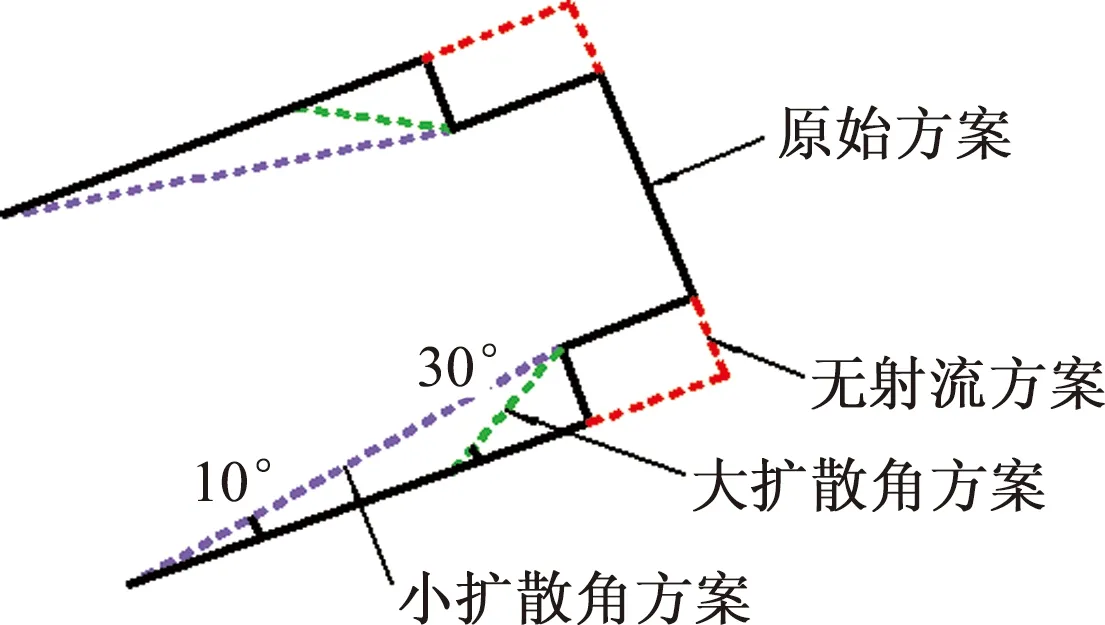
图3 进口射流扩散角影响方案示意图Fig.3 Schematic of designs with inlet jet diffusion angle

图4为进口射流扩散角影响方案速度流线图.图4a可见，当进水流道宽度相同时，速度流线很均匀；而由图4b可见，当上游流道由过流断面较小的梯形变为较大面积的矩形时，存在射流现象，如果流道过流断面扩散太快，进水流道的流动会产生较大波动.图4c和4d分别是较大和较小的流道扩散角，可见流道内的旋涡发生明显改变.

图4 进口射流扩散角影响方案速度流线图Fig.4 Streamlines of designs with different jet diffusion angles

图5为4种射流影响方案的泵进口速度分布云图，图中P1—P8分别为8个水泵进口.

图5 不同射流影响方案下的水泵进口速度分布云图Fig.5 Velocity contours at pump inlet with different jet diffusion angles

图6，7进一步表征了进口速度均匀度VZ和出口偏流角θ，最右侧代表第1台泵，最左侧代表第8台泵.

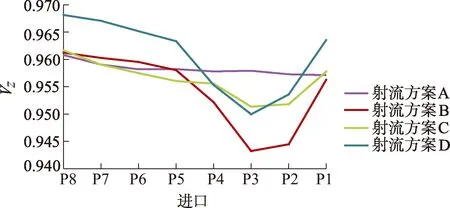
图6 射流影响方案下的水泵进口截面速度均匀度Fig.6 Velocity uniformity in cross-section at pump inlet with different jet diffusion angles

图7 射流影响方案下的水泵出口截面速度偏流角Fig.7 Velocity deviation angle in cross-section at pump inlet with different jet diffusion angles

从图5中可以清晰看出，不存在射流结构时泵各个进口的速度分布形状基本一致，且基本与y轴方向呈现对称分布，如图5a所示.而原始方案中由于存在射流，第1—2号泵进口速度明显小于其他泵进口速度，且主速度易偏向流道右侧.当射流扩散角调整后，各个泵进口速度也得到相应调整，尤其在小扩散角情况下，第4台泵进口速度明显变小.

由图6，7可知：4种射流扩散角方案中，第1和第8台泵的进口速度均匀性都优于中间位置的第5，6，7台泵；其中射流扩散角为10°时，8台水泵进口速度均匀度相比其他方案均有明显提升，因此较小射流扩散角可以显著提高水泵进口速度的均匀度，且小射流扩散角方案各水泵出口偏流角均为最小，能为水泵提供最优的入流条件.此外，无射流扩散角方案时，8台泵的偏流角差别最小，进口条件最相近.

2.3 流道曲率型线的影响

对于曲率型线，研究工作多集中在泵站流道一侧，虽然节制闸流道处曲率较明显，但是在泵站运行模式下，节制闸流道处于关闭状态，而当8台泵同时运行时，第1—3台泵内流速较低，分布不均，主流速度易发生偏移，所以对泵站流道一侧曲率型线进行优化改进，设计方案如图8所示.方案1将扩散角改到直线段处，方案2将扩散角改到曲线段处，方案3改变曲线段为直线段并适当延长扩散段长度.

图8 流道曲率型线影响设计方案示意图Fig.8 Schematic of designs with different channel curvature profiles

图9为流道曲率型线影响设计方案的速度矢量分布.由图发现，型线改变使得进水流道内速度矢量分布更加均匀，但是不同型线的上侧岸边速度矢量大小不同，其中方案3速度分布最均匀，靠近上侧岸边的速度低速区较小.

图9 流道曲率型线影响设计方案的速度矢量分布Fig.9 Velocity vectors with different channel curvature profiles

流线分布如图10所示，方案3调整了第1台泵进水池的型线结构，使主流区的流线更加光顺，使得靠近上侧岸边的低速旋涡区变小，且远离第1—2台泵进口，因此贯流泵各进口的速度分布更加均匀.

图10 流道曲率型线影响设计方案的流线对比图Fig.10 Streamline comparison with different channel curvature profiles

图11为3种曲率型线设计方案下泵各个进口的速度分布云图.图12和13分别为对应的进口速度均匀度和出口速度偏流角.

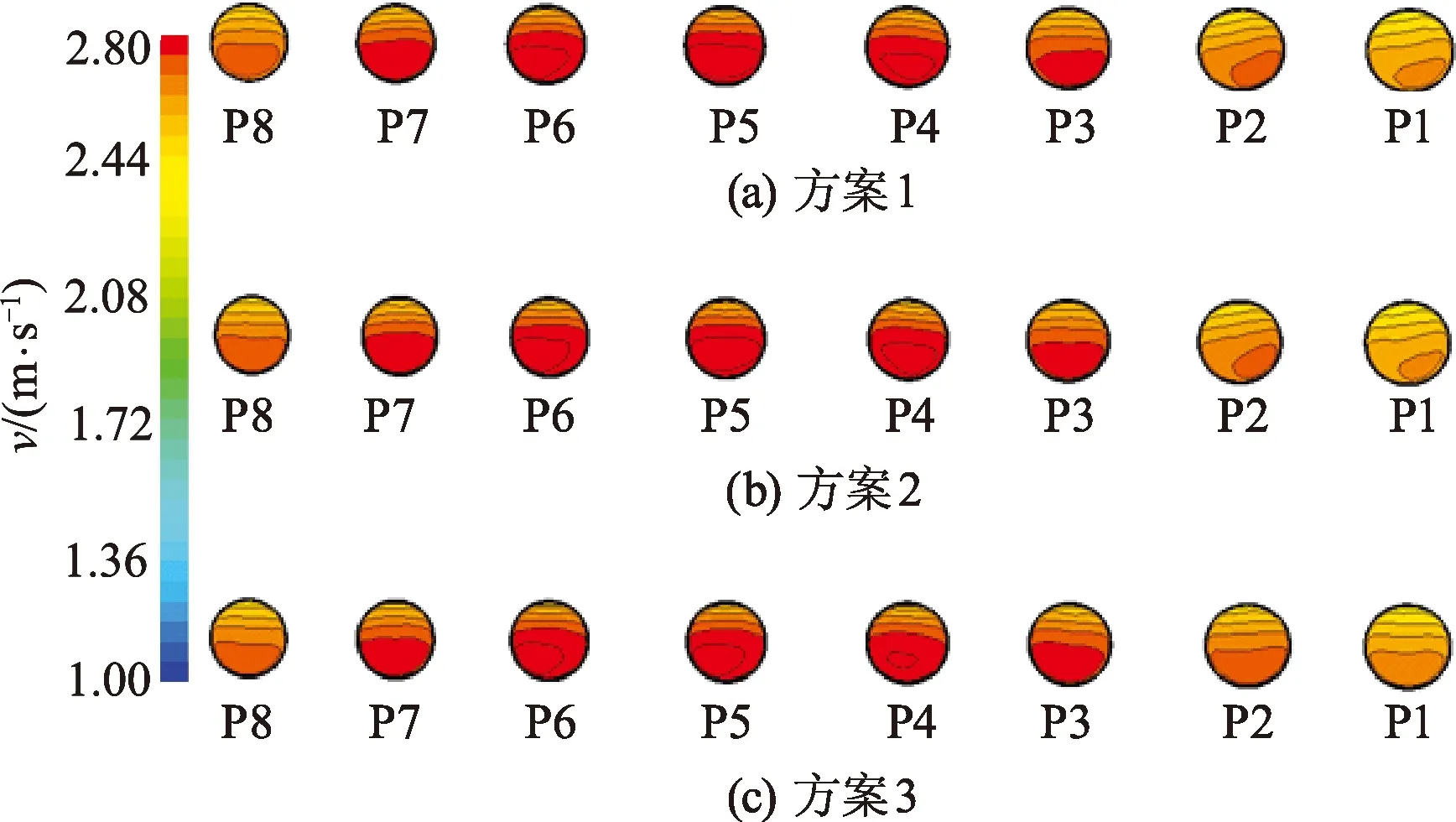
图11 流道曲率型线影响设计方案下水泵进口速度分布云图Fig.11 Velocity contours at pump inlet with different channel curvature profiles

图12 流道曲率型线影响设计方案下水泵进口速度均匀度Fig.12 Velocity uniformity at pump inlet with diffe-rent channel curvature profiles

从图11发现：改变曲率型线后，泵各进口的速度分布形状明显更加相似，说明曲率改变使得进水流道流态更加合理；不仅如此，各个泵进口的速度相对于y轴更加对称，并且相比较仍为蓝线方案3最优，红线方案1和绿线方案2在第1—2台泵进口的主流速度仍偏向右侧，这与该侧存在低速旋涡有关.由图12，13可知3种曲率型线下，8台泵进口依然是第1，8台速度最均匀，红线方案和蓝线方案下，各水泵进口都有一定程度改善，其中蓝线方案相对更优，能为水泵提供更均匀的入流.而红线方案虽然泵进口速度均匀度不如绿色和蓝色方案，但出口水流偏流角相对更小.

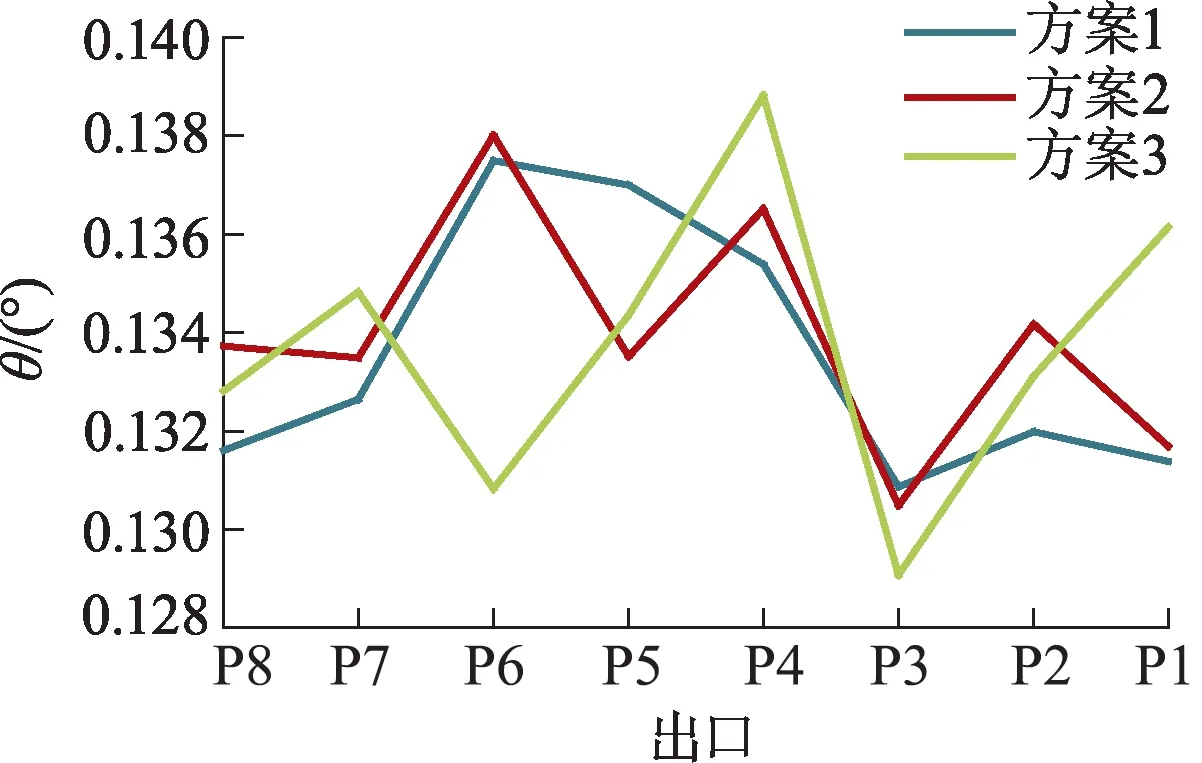
图13 流道曲率型线影响设计方案下水泵出口速度偏流角Fig.13 Velocity deviation angle in cross-section at pump inlet with different channel curva-ture profiles

2.4 导流栅长度的影响

在节制闸流道前端，由于节制闸处于关闭状态，常常形成一个较大的死水旋涡区，该涡对第8台泵的流态有一定的影响，因此设计改变导流栅的长度以改变前端的死水旋涡区[15].

图14为导流栅长度影响方案的速度矢量分布图，方案Ⅰ采用的是原始无导流栅设计方案，其他3个方案则是延长靠近第8台泵进口的导流栅长度L分别为5，10和15 m.

图14 导流栅长度影响方案的速度矢量分布图Fig.14 Velocity vectors with different flow conditioner lengths

图15为与图14对应的流线图.从图中可以看出，导流栅长度确实可以改变节制闸流道前的大涡，但是加导流栅后对整个进口流道流动产生了影响，尤其是第1—3台泵的进口流道条件变差，不仅主流道内旋涡变大并延伸到整个上侧岸边，同时泵进口流道内出现了小的旋涡.

图15 节制闸流道加装导流栅的流线对比Fig.15 Streamline comparison with different flow conditioners installed at throttle valve flow channel

2.5 节制闸流道前挡板的影响

图16为节制闸流道影响下水泵各进口速度分布云图.从图中可以看出，L=0方案的速度分布最好，而在节制闸流道前加挡板，为第8台泵进口改善流道条件后，第8台泵的速度值反而下降，且造成第1—3台贯流泵的速度值下降，主流速度更易偏向右侧，速度明显分配不均.所以，综合考虑不建议加挡板.

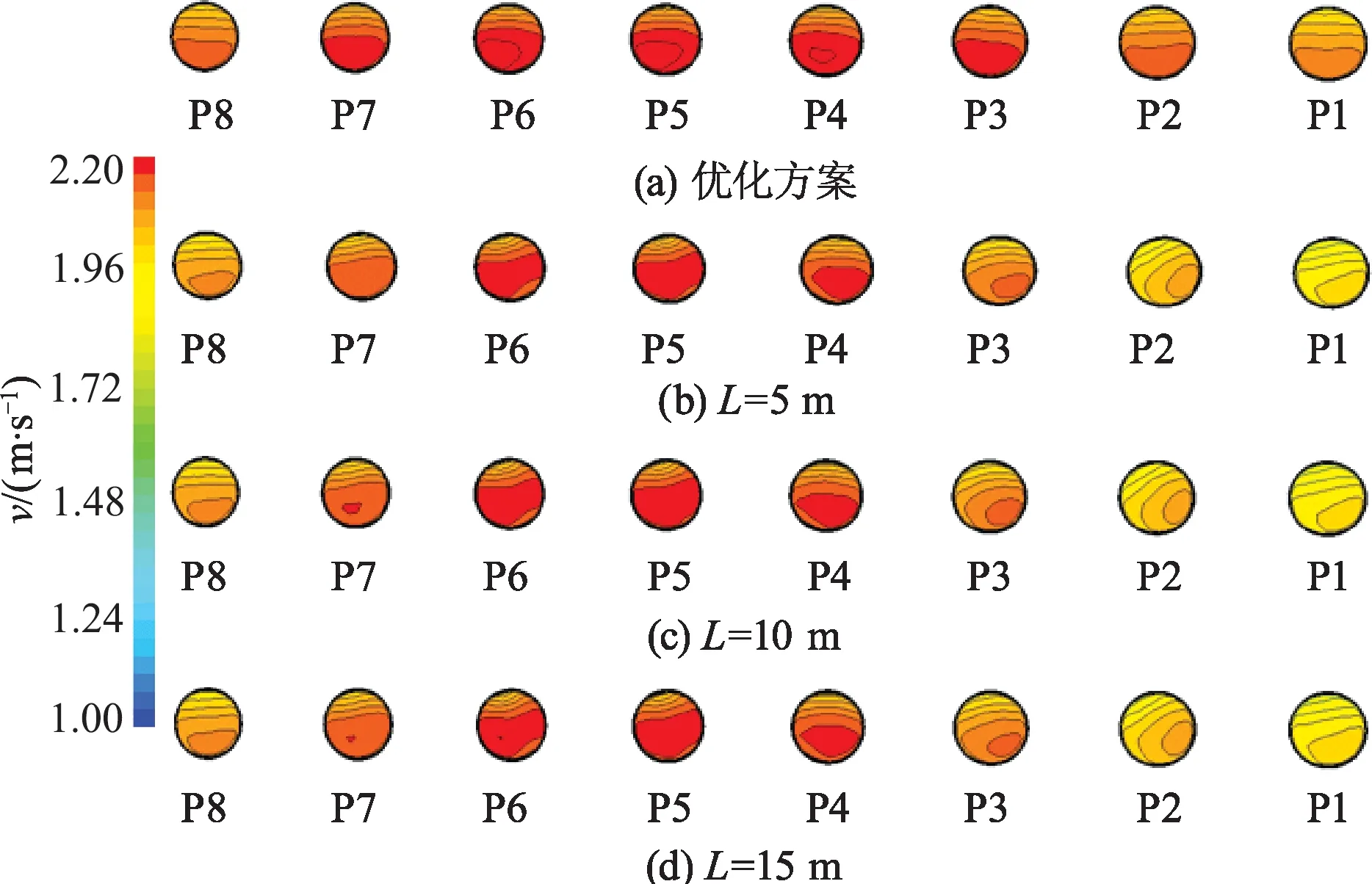
图16 节制闸流道影响下水泵进口速度分布云图Fig.16 Velocity contours at pump inlet with different flow conditioners installed at throttle valve flow channel

3 结 论

以目标闸站为研究对象，针对上游流道进口射流扩散角、流道曲率型线、导流栅长度等因素，研究不同方案对泵站上游流道流态的影响，得出以下主要结论.

1) 在进口射流方面，原始阶梯式射流结构对比无射流、大扩散角、小扩散角方案，发现较小的流道扩散角可以使流道内旋涡明显改善，水泵进口速度更均匀，出口偏流角更小，可为水泵提供更好的入流条件.

2) 流道型线改为直线段并适当延长可以使流线更加光顺，各水泵进口的均匀度得到提升.

3) 随着节制闸流道长度增大，上侧岸边的低速区明显增大，虽然适当延长节制闸流道长度可以改善流道前端的死水旋涡区，但导流栅同时会使泵进口条件变差，主流内旋涡扩大.