纺织企业质量控制数学模型的研究与应用
2021-01-19郑鸿
郑 鸿
(福州职业技术学院,福建 福州 350108)
改革开放以来,随着国民经济的不断发展,我国内需也在不断扩大,而广大消费者对产品质量则表现出越来越高的挑剔性[1]。从纺织行业的发展情况来看,很多纺织企业在产品设计、过程控制、最终产品质量等方面都存在明显的不足,事后检查的质量控制手段难以有效预防设计与生产阶段出现的质量问题,导致成品中存在很多劣质品[2]。当前,很多企业设置的检验环节只能对产品质量作出简单判断,即合格或不合格,难以作用于质量控制与提升。因此对于企业而言,如何实现高效的纺织生产质量过程管控是必须尽快解决的问题,引入数学模型是一种尝试[3]。
1 纺织企业质量控制概述
1.1 纺织企业产品质量管控的意义
结合现阶段我国纺织企业的生产经营情况来看,虽然产品质量管控方面存在明显差异,但也存在一些共同点,即产品质量管理多采用一体化的管理模式,特点是极大地简化了产品质量管理的工作内容,操作难度更低,但实际效果并不理想。因此,很多纺织企业都存在优化产品质量控制的需求,一方面是为了提高自身的竞争力,以过硬的产品质量应对越来越激烈的市场竞争;另一方面则是为了适应经济全球化的新要求[4]。随着对外开放程度的不断提高,我国越来越多的企业开始接触国际市场,想要在其中占据一席之地,必须要主动适应经济全球化的大趋势。
1.2 纺织企业质量控制存在的问题
我国很多纺织企业生产作业的过程中都存在过度追求产量而忽视产品质量的情况[5],后果就是许多存在质量问题的产品需要重新返工,导致时间成本和物料成本的不合理增加。存在质量问题的产品必然会引起客户的不满,产品不良率的频繁波动使得产品返检率居高不下,进而陷入无法交付订单的尴尬境地,不仅会使纺织企业承担一定的经济损失,还会造成企业市场信誉的降低。产品质量的低下致使企业无法在高档次市场与先进纺织企业展开竞争,随着行业的发展逐渐沦为末流,最后被淘汰[6]。
上述情况出现的原因可以归结为4点:(1)技术设备落后。对于纺织企业等生产制造企业而言,技术和设备是生产经营不可缺少的重要硬件与核心。在缺少核心技术的情况下,企业生产经营将会对其他企业产生严重的依赖性,意味着自身的存亡将受制于人,一旦合作企业撤离技术,将直接陷入瘫痪。先进的设备是生产高质量产品的必要条件,而目前我国大部分纺织企业都面临着技术和设备落后的问题。(2)质量标准体系不完善。质量标准是企业生产产品的准绳,标准的高低以及是否能够严格遵行直接影响产品的质量水平。若标准设置得过低,会给企业留下空子,无法保障纺织产品质量。若标准过高,则会造成生产成本的提高,打击企业经营者的积极性,或者标准高到纺织企业在客观上无法达到标准,这两者都会对我国纺织行业的发展造成阻碍。(3)质量管理制度不完善。完善的质量管理制度是纺织企业生产质量控制的重要依据和保障。企业的生产过程涉及多个部门的协调运作,而不同部门是由大量员工构成的,加之生产环节的复杂化,使得产品质量受到许多不稳定因素的影响,如物料质量、人员素质等。在这样的情况下,就需要通过管理制度的约束来最大限度地消除不利因素的影响,确保所有生产环节都能够顺利有序地落实。目前我国很多企业都不具备完善的管理制度,很多都是从其他企业照搬过来,与自身实际情况存在严重偏差,完全不能为生产质量控制提供有效支撑。(4)企业人员素质水平低。纺织企业生产质量相关的人员因素主要有两点:一是人员专业技能素质,二是人员道德素质。一方面,纺织企业的生产作业具有一定的技术性,专业技能素质缺陷必然会导致人员在操作过程中出现失误,引发质量问题,原因可能出在人员招聘或是培训等方面。另一方面,道德素质的不足可能会导致员工在生产过程中因为自身利益而做出损害企业利益的行为,以至于产品出现质量隐患。
2 基于数学模型的纺织企业质量控制研究
2.1 数学模型
数学模型是指基于数理逻辑方法和数学语言建构的科学或工程模型。数学模型的建构是基于某种事物系统的特征或是数量的依存关系,采用数学语言,概括或近似地表述一种数学结构。广义上讲,现今人类数学学科中涉及的一切概念都属于数学模型的范畴,包括各类理论以及公式。狭义上讲,数学模型仅指反映特定问题或特定事物系统的数学关系结构。
数学建模主要分为六大步骤:(1)准备环节工作内容包括基于实际问题背景明确建模目的,同时搜集各类信息,弄清楚对象特征。(2)模型假设,即综合对象特征与建模目的,对问题进行适当的简化处理,以精确的语言作出假设。(3)模型构成,基于假设分析对象的因果关系,利用对象的内在规律以及适当的数学工具,构建各个量间的等式关系或其他数学结构。(4)模型求解,利用各类数学方法对模型系统运行结果进行计算,通常需要使用现代化计算机技术。(5)模型分析,即对模型解答进行数学上的分析。(6)模型检验,即对数学分析的结果进行翻译,与现实问题相对照,检验模型的合理性以及适用性。
数学模型已经被广泛应用于现代社会的各个领域,为人们的日常生活、科学技术发展作出了巨大的贡献。如在经济领域用于企业成本预测和控制、在军事领域用于作战方案的制定、在司法领域用于刑事侦查中死亡时间的鉴定、在电力工程领域用于电路最大输出功率的计算等,因此将数学模型应用于纺织企业质量控制是一次可行的尝试。
2.2 纺织企业质量控制数学模型的建构与实现
基于前文所述数学模型的建构步骤,在建模之前,需要明确建模的目的并搜集所需的信息资料。建模的目的是产品质量控制,所需资料的搜集可通过产品物料清单来实现,是用于描述产品组成数量、层次关系的重要部件,在企业信息系统建构过程中占据重要地位,企业原材料和半成品都将通过它建立逻辑上的相关关系。在纺织企业生产的过程中,产品物料清单还具有维系各业务部门联系沟通的功能,覆盖了企业计划、设计、工艺、生产、供应、物料、成本、销售等诸多部门。
在纺织企业的生产作业中,前后工序存在紧密的关系,前道工序在很大程度上影响后续工序的实施效果,因此一旦某一工序出现质量问题,其后续所有工序质量都将会受到影响,且基本上不可能对前道工序中出现的问题进行修复。因此,想要实现质量控制,必须要通过智能制造系统对产品进行综合质量情况量化,即按照纺织产品的品种、过程,获得该产品在质量检验时间段内所纺纱线的总长度,依据产品质量检验标准对其质量进行实时监控,确保能够始终有效掌握产品的质量情况,并提前发现质量隐患,锁定质量不合格的产品。换言之,技术人员在产品出现质量问题前就能够依据质量标准对其进行检验、判定和处理,并根据问题产生的原因对生产线进行优化调整。
上述这种依据智能控制技术实现对纺织企业生产全过程控制的智能制造系统才是我国纺织行业生产质量控制的发展重点,而该系统的生产质量控制功能则是通过数学模型来实现的。具体内容:若假设ta和tb为纺织产品质量检验时间段的上限和下限,m和n分别是纺织产品的品种名称和过程名称,则纺织产品m在第n天的时间段(ta—tb)内所纺纱布的总长度可用式(1)表示。

式中,L(m,n,ta,tb)为纺纱总长度。
纺织产品m在第n天中的时间段(ta—tb)内第p过程中纱布每单位长度的综合质量情况量化值则可以式(2)表示。
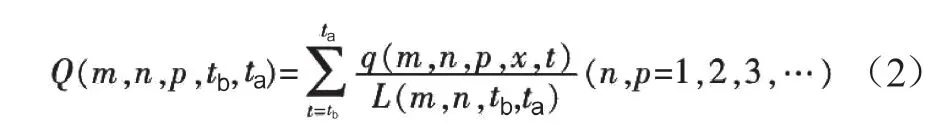
式中,Q(m,n,p,ta,tb)为纺织品综合质量情况量化值,q(m,n,p,x,t)则是指纺织产品m在第n天中第p过程t时刻影响质量因素x的测试值。
纺织产品m在第n天中的时间段(ta—tb)内第p过程中所处档位的函数关系如式(3)所示。
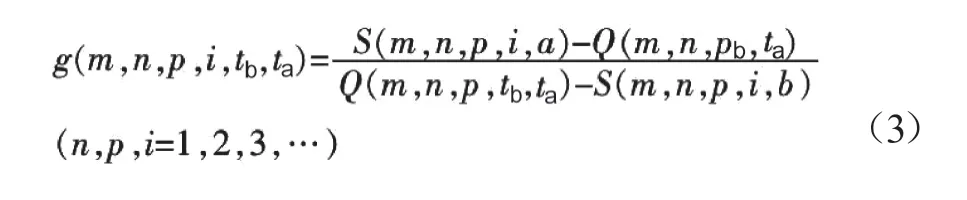
式中,S(m,n,p,i,a)为纺织产品m在第n天中时间段(ta—tb)内第p过程中的档位i所对应的标准上限值,S(m,n,p,i,b)则是指纺织产品m在第n天中时间段(ta—tb)内第p过程中的档位i所对应的标准下限值。
若g(m,n,p,i,ta,tb)>0,则纺织产品m在第n天中时间段(ta—tb)内第p过程的档位为i。因此,产品所处档位的目标函数如式(4)所示。
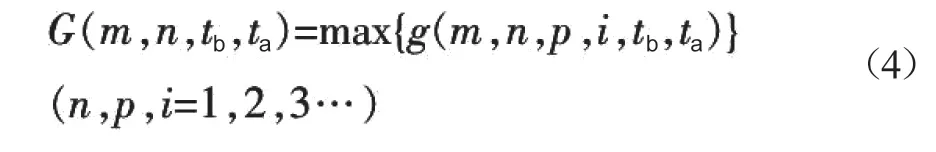
若尚存在过程没有进行,则其档位值默认为零,因此可通过该函数对纺织产品的实时质量档位情况进行表示,为纺织产品质量状况的查询、管理提供支撑,实现对质量的有效控制。在实际生产的过程中,纺织企业车间管理人员可以通过智能制造系统对所有产品的质量信息进行实时对比、分析和处理,明确质量控制的重点,并获得质量反馈信息。一旦其中某项指标超出相关质量标准要求,系统会发出警告,并锁定质量缺陷产品及其所对应的工序,避免物料的浪费。
3 结语
以数学模型为核心,利用智能制造系统对纺织企业生产质量进行控制在现实中是可以实现的。相较于传统的事后控制,这种模式能够在事前发现质量隐患,提前采取预防措施,避免质量缺陷的出现以及材料的浪费,提高企业产品质量。
