无线自组网络中的消息最优的连通控制集

唐天兵，朱继生，梁家荣

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

无线自组网可以灵活和快速地部署在许多应用程序中，例如自动化战场操作、搜索以及救灾。与有线网络或蜂窝网络不同，无线自组网中并没有安装物理主干基础设施。通信会话可以通过单跳无线传输来实现，如果通信方足够近，也可以通过中间节点进行中继。进一步假设无线自组网中的所有节点V都分布在一个二维平面上，且最大传输距离为一个单元。无线自组网的拓扑结构可以建模为单元圆盘图G=(V,E)，当且仅当两个节点之间的距离最多为1时，两个节点之间存在一条边(见图1)。

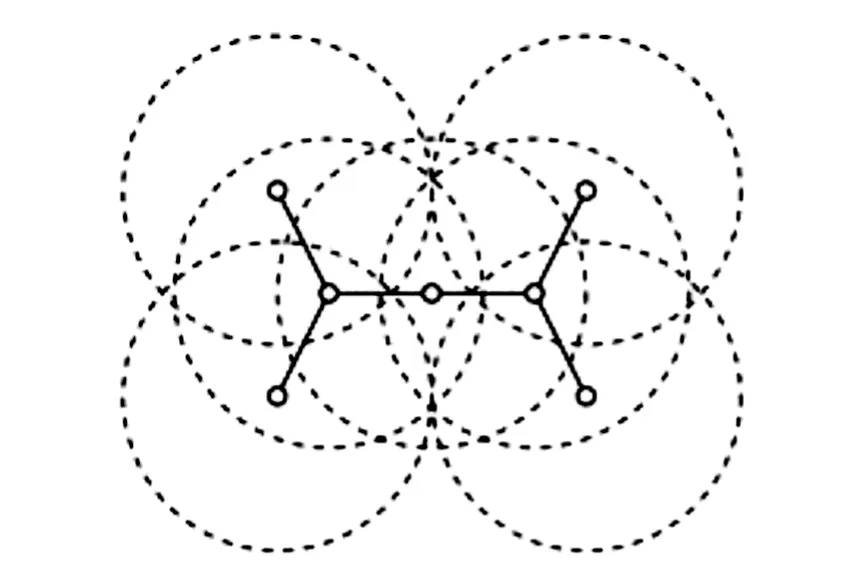
图1 由单元圆盘图组成的无线自组网

最近的研究指出，现有的ad hoc路由协议中拓扑更新或路由请求的泛洪机制大大降低了网络容量。如果将控制包的广播限制在网络中主机的一个小子集内，协议开销就可以大大减少。文献[1]研究表明：在无线传感器网络中引入虚拟骨干(virtual backbone)，可以有效地减少信息传输过程中的拥堵，极大地提高能量的使用率，延长网络的寿命．这促进了通过计算单元圆盘图中的连通控制集(CDS)构建虚拟主干的研究;文献[2]中提出的移动能量补充策略VBMERS能有效地解决节点的能量饥饿问题，降低节点的失效率，进而延长传感器网络的生存周期。

近年来，关于连通控制集的构造算法己经有很多的研究。因为虚拟骨干网的规模会影响网络性能，因此如何构造最小连通控制集(MCDS)也就成为了研究的热点。虽然构造最小连通控制集早已被证明是NP难问题，但仍然有很多算法用于构造MCDS，主要分为以下几个种类。

第一类主要是用于构造一般CDS，主要是基于文献[3]中剪枝、文献[4]中极大独立集和文献[5]中图着色等一系列方法。

第二类主要是用于构造多跳CDS上。比如文献[6]中基于剪枝的r-hop CDS构造方法和文献[7]中d-Hop 2-连通容错支配集的分布式构造算法。

第三类主要是关注于控制集的容错性和可靠性等方面，如文献[8-9]和文献[10-11]，其中大多与m-控制、k-连通性有关系。

而在无线自组网中，虚拟骨干网的质量通常是由其近似因子来衡量的，近似因子是骨干网的大小与MCDS的大小之比;而虚拟骨干网的建设成本是通过消息复杂度和时间复杂度来度量的。表1总结了文献[12-14]中提出的虚拟骨架的质量和构建成本。在节点可以连续移动的移动无线自组网中，虚拟骨干网不仅要时刻保持良好的质量，而且在某一特定时刻，还要允许由于拓扑变化而进行有效的维护。遗憾的是，文献中提出的虚拟骨干都不能有效地维护以保持良好的质量。

表1 CDS构造算法的性能比较

1 相关理论与定义

无线自组网是由无线接收机、发射机等移动终端组成的多跳、自组织的自治网络。蜂窝移动通信网络和无线局域网都需要预定义的基本网络设施，如基站和接入服务站。然而，作为一个分散的分布式控制系统，在无线自组网中，每个用户都具有路由器和主机的功能。因此，方便的终端可以实现简单、快速的无线通信。无线自组网不依赖于任何现有或预定义的网络基础设施，终端节点随机分配。因此，如何保证终端节点移动时的高质量信号通信是研究领域的一个关键问题。无线传感器网络是分散的分布式系统。大量的传感器以随机的方式密集地布置在监测区域内。传感器网络用于从给定的位置或区域收集分布式信息。这些网络由微型设备组成，每个设备都配有电源、微控制器、无线接口、少量内存和一个或多个传感器。传感器用于收集物理参数，如光强度、声音或温度。由于无线通信范围有限，传感器节点通过中间节点进行无线多跳路由通信。无线网络包括无线自组网和无线传感器网络，近年来受到越来越多的关注，并在战场、灾难恢复、会议、音乐会、环境检测、健康应用等方面得到了广泛的应用。

人们普遍认为，无线网络将是下一代网络提供灵活部署和移动连接的理想和重要组成部分。为了研究无线网络的算法和性质，并对其正确性和性能给出数学证明，提出了许多模型，在此基础上，给出了CDS相关的定义和术语。

单位圆盘图(UDG):设V⊂R2为二维平面上的一组节点。这个欧几里得图G=(V,E)被称为一个单位圆盘图，如果图中任何两个节点相邻当且仅当它们的欧几里得距离最多是1。对于任意u,v∈V，它都有{u,v}∈E⟺d(u,v)<1。假设具有全向无线电天线的节点部署在一个平面的、畅通无阻的环境中。当且仅当两个节点在相互传输范围内时，它们是相邻的。图1显示了一个UDG示例，其中圆圈表示传输范围。可以看到所有节点的传输范围都是相同的。CDS构造算法大多基于UDG的特点。然而，UDG模型是非常理想的。在现实中，无线电并不是全方位的，甚至像植物这样的小障碍也能改变连通性。

独立集(IS)和极大集(MIS):对于给定的G=(V,E)，一个子集I⊂V是G的一个独立集，如果每一对u,v∈I，(u,v)∉E。一个独立集I被叫做极大独立集则是如果不存在节点w∈VI，这样的I∪{w}仍然也是G中的一个独立集，则称其为最大独立集。

控制集(DS)和连通控制集(CDS):对于给定的G=(V,E)，一个子集D⊂V是G的一个控制集，如果每一个u∈VD，这里存在另外的点v∈D，都满足(u,v)∈E。如文献[15]所说找到一个最小控制集MDS是NP困难。一个控制集D，其诱导子图G[D]是连通的，则称其为连通控制集。

最小连通控制集(MCDS)：MCDS是具有最小基数的CDS。从文献[16]中可知MCDS也是NP困难。

2 多跳极大独立集模型

引理1：文献[16]中设S为单位圆盘图形G中的任意极大独立集。对于∀u∈S，证明S中距离u最多2跳的节点数最多为23；对于∀u,v∈S，如果u,v相距两跳，那么S中距离u或v最多3跳的节点数最多为64。

引理2：设S为单位圆盘图形G中的任意极大独立集。对于∀u∈S，S中距离u最多3跳的节点数最多为44。

证明：注意到之前的模型都是用R为0.5的圆来模拟多跳无线网络中的独立节点，然而应该注意到一个事实，即圆与圆之间并不是密铺的，会存在一定的间隙。因此，用正六边形来替代圆的话，会得到更为精确的结果，如图2所示。

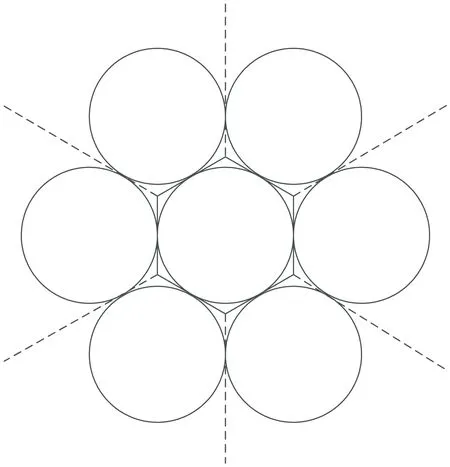
图2 正六边形替代单位圆盘

然而当正六边形在边界上的时候有一个凸起会处于边界外面(见图3)，因此可以舍弃掉一个阴影部分的面积，为每一个R为0.5的圆分配5个阴影部分的面积来进行计算。

图3 阴影部分

3 近似因子分析

为了达到最低消息复杂度的目标，其构造方法如图4所示，主要包含三个步骤：步骤1构造一个森林，其中每棵树的根在其一跳邻居中ID最小的节点上；步骤2收集邻接信息；步骤3用于连接邻接树。最初所有节点都是白色的。操作和广播消息如文献[16]所述。

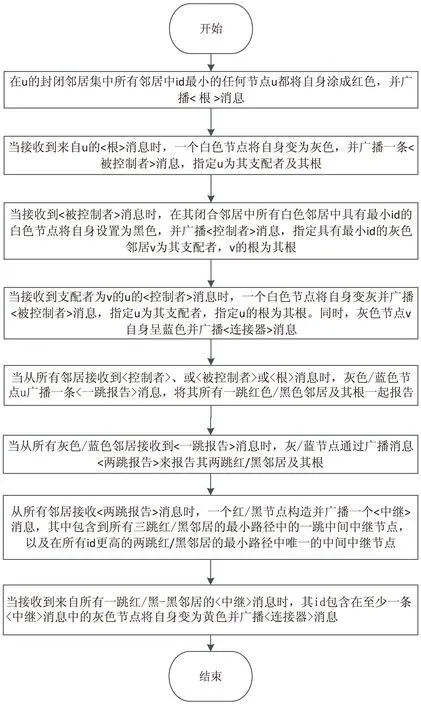
图4 构造方法

定理：所生成的连通控制集的大小最多为143·opt+33。

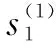
从文献[16]中可知：

|S1|+|S2|≤4·opt+1

且

|S3|≤|S2|

2-|S3|

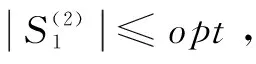
D=|S1|+|S2|+|S3|+|S4|≤

44≤143·opt+33

4 结束语

该文在保证构建消息最优的连通控制集的情况下，建立了一种新的求解极大独立集的模型，注意到在之前的文章中都是通过圆来建立求解三条内的极大独立集，但是显然在圆与圆之间是有缝隙的，这会造成一定的误差。而通过使用正六边形来代替R为0.5的圆，显然可以求得一个更为精确的三跳内极大独立集，从而提高了结果的准确度，得到了一个更小的其值为143opt+33连通控集近似比。在文献[17]中证明了单位磁盘图中的MCDS有一个PTAS，这意味着它可以被近似到任何程度。然而，具有O(nlogn)消息复杂度的最佳算法的性能比为8，线性消息复杂度的最佳算法得到的连通控制集最多为143opt+33，因此，未来的研究之一是设计更好的启发式算法来弥补这一差距。