基于多遗传算法的BP神经网络人脸识别

曾 坤，姜志侠

(长春理工大学 理学院，吉林 长春 130000)

0 引 言

随着时代的进步，科技的不断发展，在许多领域出现了新兴技术。这些技术的出现也不断地推动着其他领域的发展，同时一些新的需求也不断体现出来。而人脸识别技术正是在这样的背景下应运而生的。人脸识别的应用十分广泛，例如门禁系统[1]、银行业务[2]、公安犯罪嫌疑人侦查[3]等。近几十年，人脸识别技术发展迅猛，吸引了各个领域的学者参与研究[4-5]，应用前景广泛，具有重要的现实意义。

人脸识别是一种基于人的脸部特征信息进行身份识别的生物识别技术[6]。人脸识别一般主要分为三个步骤：一是人脸图像获取，二是人脸特征提取，三是人脸识别。学者们也提出不少相关算法。1901年统计学家Karl Pearson[7]提出了PCA(principal components analysis)算法，PCA算法将高维的数据映射到低维空间，并保留了原数据的一些特征．该算法广泛用于数据降维、数据压缩等。Herault等人[8-9]针对盲源信号的分离提出了ICA(independent component analysis)算法并加以发展．其中1997年Hyvarinen[10]提出的FastICA算法，具有收敛速度快、分离效果好的优点。近年来，一些学者[11-12]将ICA算法用于模式识别，并且取得了较好的效果。1986年Rumelhart等人[13]提出了按误差逆向传播训练的BP神经网络算法，广泛用于模式识别、目标分类等。

该文提出了一种基于多遗传算法优化BP神经网络结构和权值阈值的人脸识别方法。对人脸图像的预处理采用了PCA和FastICA算法，更大程度上提取人脸图像的特征，有利于后续的识别工作。首先用PCA算法对人脸图像进行降维，用FastICA算法提取降维后的人脸图像特征。针对BP神经网络易陷入局部最优、收敛速度慢等缺点，主要采用遗传算对BP神经网络的训练函数、训练次数、隐藏层的层数、隐藏层的神经元个数和权值阈值进行优化处理。仿真实验结果显示，识别率有了一定程度的提高。

1 人脸特征提取

1.1 ORL人脸数据库

该文采用ORL人脸数据库进行仿真，ORL人脸数据库共由40个人脸样本组成，每个人脸样本各10张，共计400张人脸图像。每张人脸图像尺寸均为92*112，包含不同性别、年龄以及种族等。其中部分人脸有不同的面部表情，微笑、张嘴以及是否戴眼镜等。各张人脸之间存在的一定差异，对识别的算法具有较高的检测能力。在人脸库中随机选取5张人脸组成训练集T，每一个人中剩余的5张人脸组成测试集Y。对训练集进行数字化处理，将每一张的人脸的灰度值按列连接成10 304×1维的列向量，从而将训练集200张人脸图像处理为10 304×200维的矩阵。对于测试集做同样的处理。

1.2 PCA算法

PCA算法是一种较为常用的降维算法，PCA算法的主要思想是截取较高贡献率的特征值对应的特征向量，从而构成比原数据维度较低的变换矩阵，通过线性变换将高维数据沿着方差最大的方向投影到低维空间。对于人脸训练集T=(t1,t2,…,tn)，共有n张人脸样本，每张人脸用向量表示为ti=(t1i,t2i,…,tmi)T，计算n张人脸的均值，平均脸为：

计算每一张人脸与平均脸的差值：

平均脸和去均值人脸如图1所示。

图1 平均脸(左)和去均值人脸(右)

令P=(p1,p2,…,pn)，构建人脸的协方差矩阵：

C=PPT

传统的主成分分析算法是通过样本的协方差矩阵特征值分解进行的。但是对于高维数据，即样本的维度m很大的时候，协方差矩阵为m×m维，导致计算量非常大。为了避免上述问题，通常对样本采用SVD(singular value decomposition)的思想进行处理，构造矩阵：

P=UΣVT

特征值数量与特征值贡献率的关系如图2所示。

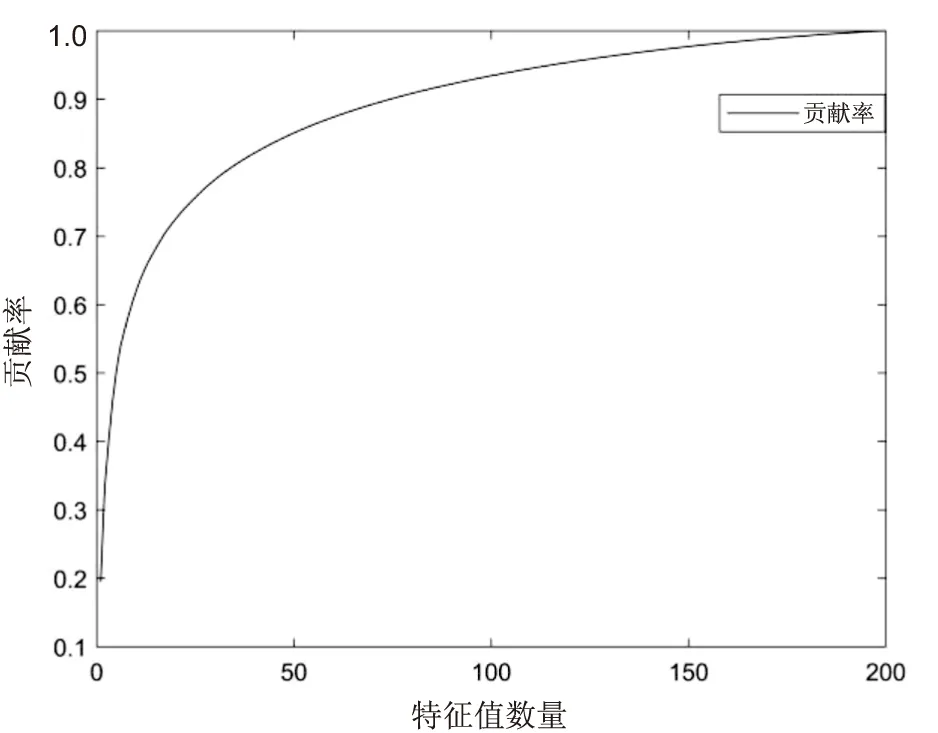
图2 特征值贡献率

由图2可以看出，较大的特征值贡献较多的能量。选取前k个贡献率较多的特征值对应的特征向量，从而计算得到投影矩阵U=(u1,u2,…,uk)T，使得投影后的数据维数比原数据维数低。将投影矩阵还原为人脸像素则可得到特征脸，其特征脸如图3所示。

图3 特征脸

1.3 基于负熵的FastICA算法

FastICA算法处理的数据要求各个分量之间是统计独立或者尽可能独立[14]，因此在1.2中对人脸图像用PCA算法进行了预处理，消除变量之间的相关性。FastICA算法是ICA算法的改进，由于收敛速度快、效果好而得到广泛应用。本节采用FastICA算法对人脸图像进行特征提取。设观测样本数据X为m×n阶的矩阵，共有n个数据，每个数据为m维。

独立信号源为：

即有混合矩阵A，使得X=AS，从而寻找一个恢复矩阵W，使得B=WX，让B逼近于S。Hyvarinen等人[15]改进了FastICA算法，用负熵来度量非高斯性，最大化负熵使得非高斯性最大。采用较为经典的负熵近似公式[16]作为目标函数：

J(y)=[E{g(y)}-E{g(yGauss)}]2

其中，J(y)为随机变量y的负熵，E{·}表示均值，g为非线性函数，取为：

导函数为g'(y)=tanh(a1y)。经过化简后得到FastICA的迭代公式为：

对迭代后的恢复矩阵进行归一化处理：

若W未满足收敛条件，则重复上述过程直到收敛。计算投影矩阵B：

B=WX

训练集T在投影矩阵B下的投影为TB=BTT，测试集Y在投影矩阵B下的投影为YB=BTY。其独立成分人脸图像如图4所示，对比图3可以看出，经过FastICA算法处理后，人脸特征更加明显。

图4 FastICA算法处理后的人脸

2 多遗传算法优化BP神经网络

2.1 遗传算法优化BP神经网络结构

遗传算法作为启发式算法的一种，通过概率的方式进行选择、交叉、变异。在多次迭代的子代种群中选择优良的个体，能够有效地寻找全局最优解。而BP神经网络的结构往往依靠经验选取，对于训练函数、训练次数、隐藏层层数及每一个隐藏层的神经元个数较为敏感。本节采用遗传算法对上述结构进行优化，在一定程度上避免了BP神经网络陷入局部最优、收敛速度慢等问题。

染色体的设置：在一般的遗传算法中，染色体为等长的染色体，但是文中由于BP神经网络隐藏层层数的变化，染色体的长度可能不一样，因此设计染色体为变长的染色体。编码方式为正整数编码，每一个基因位的意义表示为：第一个基因位为BP神经网络的训练函数；第二个基因位为BP神经网络的训练次数；第三个基因位为BP神经网络隐藏层的层数；第四到第六个基因位为BP神经网络隐藏层每一层的神经元个数。其中第三个基因位的值决定了剩下基因的位数，染色体的格式为X=[x1,x2,x3…]，每一个基因的取值范围为：

初始种群：采用随机化的方法初始种群，在保证每个基因的值满足其对应的约束情况下随机生成染色体。例如染色体X1=[2,5 230,2,41,36]，则X1表示选用的训练函数为第二个函数，BP神经网络的训练次数为5 230，BP神经网络的隐藏层层数为2层，第一个隐藏层的神经元个数为41，第二个隐藏层的神经元个数为36。

适应度值计算及选择操作：本节遗传算法主要优化BP神经网络结构，以此提高人脸图像的识别率，因此将识别率作为适应度值。选择操作采用轮盘赌方法，每个个体被选中的概率为：

其中，fi是第i个个体的适应度值，N是种群大小。

交叉：由于染色体是变长的，染色体的交叉采用基于随机交叉点的混合交叉方式。交叉点为随机生成的正整数，最大值为较短染色体长度。当随机交叉点的值为[1,3]时，采用单点交叉，以随机交叉点为基准互换两条染色体配对部分。当随机交叉点的值为[4,6]时，即为隐藏层的神经元个数基因位时，采用两点交叉，在染色体中随机选择两个交叉点。其中两个交叉点值均大于3，但是小于等于较短染色体的长度，然后两条染色体互换交叉点内的基因。

对于交叉概率的设置，常规的遗传算法采用固定的交叉概率，使得较小和较大适应度值的个体具有相同的交叉概率。对于较大适应度值的个体可能被破坏，应需要较小的交叉概率，尽可能地保留较好的个体。对于较小适应度值的个体，应需要较大的交叉概率，通过交叉的方式获得更好的基因，因此采用自适应的交叉概率，对于较大适度值的个体自动调整交叉概率，获得较小的交叉概率，较小适应度值的个体则获得较大的交叉概率。其自适应交叉概率[17]如下：

其中，fmax为种群中的最大适应度值，fc为待交叉个体适应度值，favg为种群中的平均适应度值，k1,k2为常数。

变异：变异采用单点变异的方法。当变异点的基因位不为3的时候，则随机生成一个对应基因值域范围内的值进行变异。当变异点的基因位为3时，即BP神经网络的隐藏层层数发生变异，则随机生成一个层数值域范围内的变异值，若变异值小于隐藏层层数，则隐藏层的基因位相应减少，若大于隐藏层层数，则隐藏层的基因位相应增加。对于变异概率同交叉概率一样，采用自适应的变异概率[17]，其公式如下：

其中，fmax为种群中的最大适应度值，fm为待变异个体的适应度值，favg为种群中的平均适应度值，k3,k4为常数。

2.2 遗传算法优化BP神经网络权值阈值

BP神经网络是基于误差减小反向更新权值阈值的，对初始权值阈值较为敏感[18]，若按照传统方式随机选取网络的初始权值阈值，则有可能在BP神经网络训练过程中陷入局部最优等问题，因此采用遗传算法对BP神经网络的权值阈值进行优化。

染色体设置：该网络中权值阈值数量多，若采用单染色体，则每条染色体长度十分大，在交叉变异中不利于个体进化。因此改进单染色体为多染色体并行执行，使得每一层的权值阈值都得到有效优化。对于2.1中得到的BP神经网络结构，例如：一个输入层，一个隐藏层，一个输出层，则会有两组权值，输入层到隐藏层权值，隐藏层到输出层权值，两组阈值，输入层到隐藏层阈值，隐藏层到输出层阈值。一共有四条染色体，分别记为W1,W2,B1,B2。每组染色体初始化为-0.5～0.5之间的随机值，共四组对应子种群。设种群为：pop=[popW1,popW2,popB1,popB2]。

适应度值计算：将初始化的染色体传入BP神经网络，通过2.1确定BP神经网络的结构，对BP神经网络进行训练。用训练好的BP神经网络计算人脸测试集的识别率，把识别率作为适应度值。

选择运算：采用父子竞争[19]的选择方法。遗传算法在交叉运算时会选择两组父染色体，进行交叉操作后产生两组子代，一共四组染色体。计算这四组染色体的个体适应度值，选取适应度值较大的两组染色体进入变异环节。在变异操作中，每组染色体经过变异后又会产生一组子代．计算子代和父代的适应度值，将适应度值较大的个体保留到下一代。在迭代完成后选择种群中适应度值最大的个体作为最优个体输出。

交叉：从种群中选择对应两组父染色体进行交叉，采用单点交叉，随机选择交叉点位置，将交叉点后面部分的基因进行相互交换。由于个体适应度值变化不是特别大，因此采用固定交叉概率，交叉概率为0.8。

变异：在该遗传算法中，染色体较长(基因数可能为1 000左右)，因此选取多个基因进行变异。根据经验值选取变异的基因个数为基因总数的5%(取整)，然后随机选择变异基因的位置进行变异，变异概率为0.1。

2.3 基于多遗传算法的BP神经网络

BP神经网络模拟生物神经网络的信号传递，将模型的信息存储在神经元、权值和阈值中，通过误差反向传播来训练网络。多遗传算法优化BP神经网络步骤如下：

步骤1：对人脸图像进行降维特征提取。

步骤2：用遗传算法对BP神经网络的训练函数、训练次数、隐藏层层数和隐藏层神经元个数进行优化。为了结果的有效性，采用控制变量法，对构建的BP神经网络的权值阈值初始化相同的值。

步骤3：用步骤2得到BP神经网络结构参数，构建BP神经网络。用遗传算法对BP神经网络权值阈值进行优化。以BP神经网络的识别率作为遗传算法的适应度值，当BP神经网络的权值阈值最优时，BP神经网络的识别率达到最大。

步骤4：保存步骤3得到的最优识别率和对应的BP神经网络，输出最优识别率，整个算法流程如图5所示。

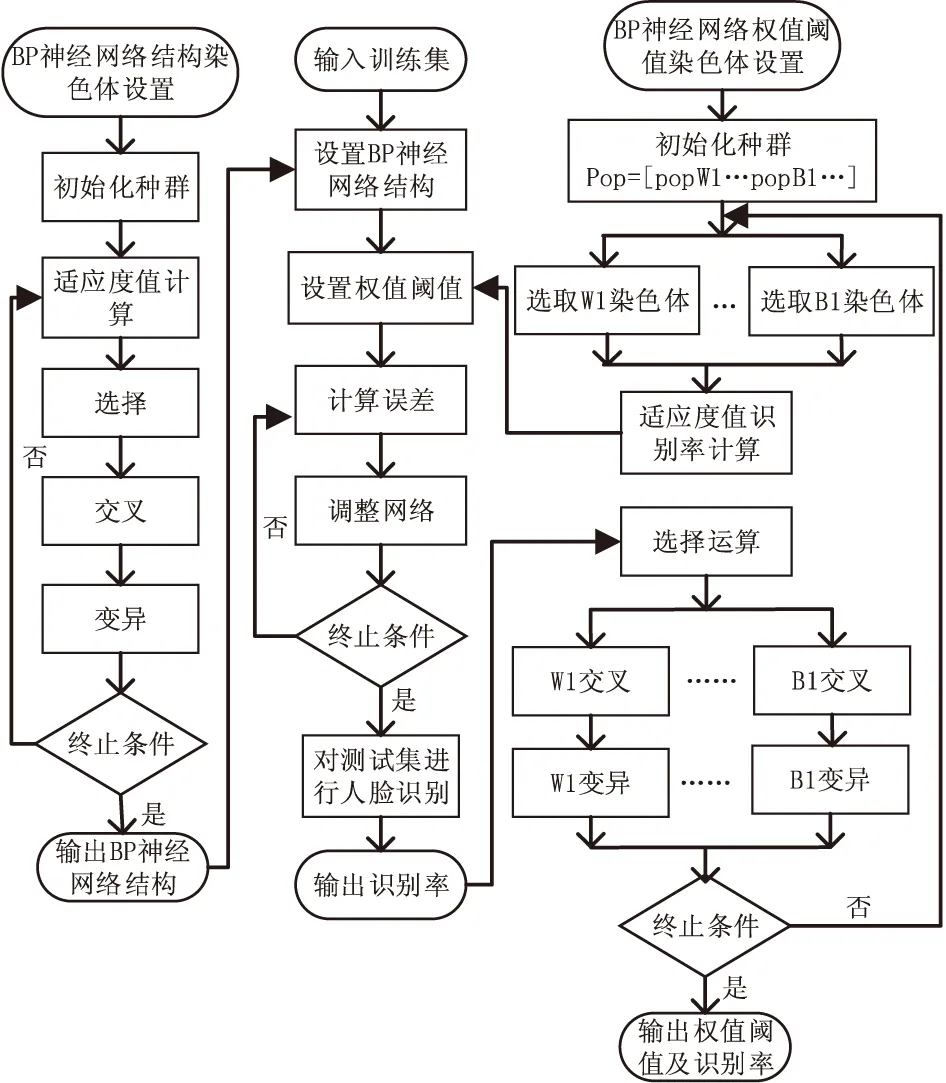
图5 算法流程

3 数据仿真实验

参数选取，两层遗传算法种群均为50，迭代次数均为10次，BP神经网络目标误差为0.001，默认学习率0.05。

用PCA算法选取前35个特征值对应的特征向量对人脸图像进行降维，然后用FastICA算法进行特征提取，对BP神经网络优化处理后，用BP神经网络对测试集进行识别。经过15次重复实验，平均识别率为0.972 7，最高识别率可达0.985。其多次实验的识别率以及平均识别率如图6所示。

在文献[20]中，作者利用PCA算法提取人脸图像中的主要特征，采用最近邻分类器进行分类，其识别率为0.925。在文献[21]中，作者采用主成分分析对人脸图像进行特征提取，利用BP神经网络预测人脸识别率，其识别率为0.941。在文献[22-23]中，作者用PCA和FastICA两种技术对人脸特征进行提取，其识别正确率最高为0.950。文中采用多遗传算法优化BP神经网络进行人脸图像识别，其多次实验平均识别率为0.972 7，说明该算法具有良好的性能，识别率较高。文中算法与其他算法对比如表1所示。

图6 多次重复实验结果

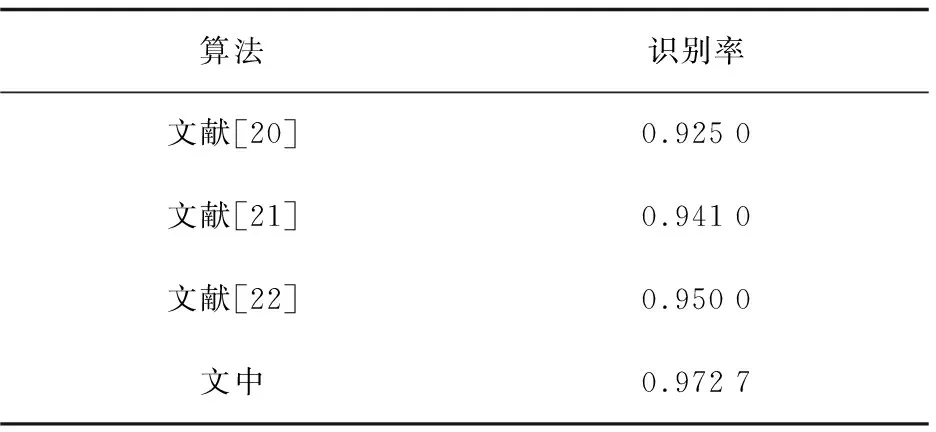
表1 算法对比

4 结束语

BP神经网络在各个领域中的应用十分广泛，特别是对于一些没有明确模型的复杂问题，BP神经网络能够很好地解决。但是目前来说对于BP神经网络结构和权值阈值的选取没有一套完整确定的理论，一般都是凭借人们的经验去选择。而遗传算法可以在一定程度上弥补BP神经网络的不足。文中先利用PCA和ICA算法对人脸图形进行降维和特征提取，然后采用多遗传算法优化BP神经网络，这样避免了BP神经网络结构及权值阈值选取的随机性，在一定程度上提升BP神经网络的性能。最后用优化训练好的BP神经网络在测试集上进行人脸识别，其实验仿真结果显示该算法性能良好。在重复实验过程中，多次出现识别率为0.975，即测试集中有5个样本不能被正确识别，猜测数据集中可能有两张人脸为双胞胎或高度相似，因此识别双胞胎或高度相似人脸将是未来的研究方向之一。