基于评分填充和时间的加权Slope One算法

刘金梅，舒远仲，张尚田

(南昌航空大学 信息工程学院，江西 南昌 330063)

0 引 言

随着互联网的不断发展，产生的数据量越来越多，面对海量的数据，人们很难准确而快速地找到自己感兴趣的物品，为解决此问题，推荐系统应运而生[1]。推荐算法是推荐系统的核心，常用的推荐算法是协同过滤算法[2]，该文研究的加权slope one算法[3-4]是协同过滤算法的一种，它计算简洁、容易实现，但是在数据稀疏情况下算法预测效果仍然较差，因此许多学者针对数据稀疏性进行了研究。研究者使用了数据填充[5]、随机游走[6]、神经网络[7]、矩阵分解[8]等技术，以提高推荐算法的精度。最简单的方法是对评分矩阵中的空缺值进行填补[5]。夏建勋等人[9]采用数据的平均值、中位数和众数三种方式进行填充，虽然可以缓解数据稀疏问题，但是这些填充方法没有考虑用户和项目本身的特性；李欢[10]提出一种基于项目相似度的协同过滤算法，实验结果证明可以有效缓解数据稀疏问题；马铁民等人[11]提出一种结合用户相似度，并采用随机游走技术进行推荐的方法，可以提高推荐精度；龚敏等人[12]首先根据用户特征进行聚类，再使用slope one算法预测并填充数据，最后根据填充数据进行推荐，可有效缓解数据稀疏性；王永康等人[13]使用融合时间信息的隐语义模型对原始评分数据进行填充，同时时间因素也能反映用户的兴趣爱好变化，提高了推荐精度。

上述针对数据稀疏性问题进行的研究都取得了不错的效果，但是该文考虑到用户评分易受到主观性以及环境等其他因素的影响，导致用户对项目的评分或高或低甚至没有评分，此种情况下用户的评分无法准确地衡量用户对项目的偏好，而项目的属性一直都比较稳定，因此可以根据用户对项目属性的偏好间接体现用户对项目的喜好程度，故提出一种新的评分矩阵填充方法。基于填充后的评分矩阵，又考虑到用户兴趣爱好随时间会发生变化，于是引入时间因子，提出一种融合用户属性偏好特征和时间因子的加权slope one算法。

1 算法设计

1.1 填充用户-项目评分矩阵

随着数据量的不断增大，用户-项目评分矩阵变得越来越稀疏，面对数据的稀疏性，常用数据的平均数、中位数和众数等来填充用户对项目未评分数据[9]。该文提出一种新的用户对项目未评分数据的填充方法，主要是通过用户对项目的偏好以及用户对项目的平均分进行加权填充未评分项目。具体方法如下：

设总共有m个用户U={U1,U2,…,Um}和n个项目I={I1,I2,…,In}组成的用户-项目评分矩阵Rmn，则用户-项目评分矩阵如式(1)所示:

(1)

矩阵Rmn为m行n列的用户项目评分矩阵，其中用户Ui对项目Ij的评分用Rij表示，若用户对项目没有评分，则其值为0。评分反映了用户对项目的偏好程度。

由式(1)用户对项目的评分，计算每个用户对项目的平均评分，则平均评分计算公式如下：

(2)

其中，Rui_avg表示用户u对项目i的平均评分；sum(Rui)表示用户u对项目i的评分总和；num(Rui)表示用户u对项目i评分大于0的项目总数。

将用户对项目的平均评分转化成对角矩阵，如式(3)所示：

(R_avg)mm=diag(Rui_avg)

(3)

其中，m为用户数量，对角线上的值为用户对项目的平均评分。

每个项目都有各自的属性类型，设有n个项目，项目属性类型共有k个，则构建项目-属性矩阵，如下式所示：

(4)

其中，Tnk为项目-属性矩阵，矩阵中数值Tij取值为0或1，若项目i属于属性类型j，则Tij取值为1；否则，Tij为0。

根据项目-属性矩阵可以计算出用户对项目属性的偏好值，计算公式如下所示：

(5)

其中，num(Tuj)表示用户u评价j类项目的数量；num(Iu)表示用户u已评分的所有项目数量。

当某个项目非常流行时，大多数人会对该项目评高分，而此时项目属性类别反映的则是该项目的流行度，并不能由此得出用户对项目的个性化偏好，因此，需要降低高频率属性对项目属性的影响，于是引入权重因子优化项目-属性矩阵。权重因子计算公式如下所示：

(6)

其中，num(pi)表示用户喜欢的具有属性pi的项目数量；sum(num(pi))表示所有用户喜欢的具有属性pi的项目数量的总数。

将权重因子转化为对角矩阵，公式如下所示：

(W)kk=diag(Wpi)

(7)

将式(7)中的权重因子与原始的项目-属性矩阵(式(4))相结合即得到加权项目-属性矩阵，公式如下所示：

(8)

由用户对项目属性偏好值(式(5))以及加权项目属性矩阵，可以得出用户对项目的偏好值，计算公式为：

P(u,i)=(Puj)mk*Tnk'

(9)

通过用户对项目的偏好值(式(9))乘以用户对项目的平均评分(式(2))来填充原始用户-项目评分矩阵，填充后的评分矩阵可以有效缓解数据稀疏性。

1.2 属性兴趣特征向量

传统的协同过滤算法仅仅考虑用户评分，根据评分矩阵区分用户对项目的喜爱程度，但是在数据比较稀疏时，无法准确地知道用户的偏好。日常生活中，用户兴趣特征主要体现在一种或者多种项目类别上，也就是对于项目或者商品用户具有类别属性偏好[14]。用户的评级有主观性，并且很容易受到环境等其他因素的影响，用户会对项目给予较高或较低的评分，最终导致评分数据的不真实；而每个项目都有自身的属性特征，并且项目属性特征比较稳定，因此，可以通过构建项目-属性矩阵代替原始用户-项目评分矩阵，通过项目-属性矩阵计算用户的偏好，相比于原始的评分矩阵可以更好地反映用户在多方面的兴趣特征，可以有效改善数据的稀疏性，可以获得较准确的用户相似度，从而能够提高推荐精度。

由式(5)计算出的用户对项目属性的偏好度，构建用户-属性兴趣矩阵，如下式所示：

(10)

其中，Pmk表示用户对项目属性的兴趣矩阵，公式中的值为m个用户对项目类型k的偏好值，偏好值越大表明用户对该类型项目越感兴趣。

通过用户对项目属性的兴趣矩阵，将用户对项目属性的兴趣矩阵转化为用户对项目属性的特征向量。若用户u对项目i有评分，而项目i所属类型有k类，如何求出用户u对项目i属性的偏好值。可以根据用户u对k类偏好值的总和求得用户u对项目i属性的偏好度，如式(11)所示：

(11)

其中，num(pi)表示项目i所属类型的数量。

用户u对项目i属性的偏好度Pui即为属性兴趣特征向量，与原始用户-项目评分相比，其中包含数值0的数量更少。在共同评分很少甚至没有时，可以通过属性兴趣特征向量计算用户间的相似度，相比于原始评分数据，可以有效缓解数据稀疏性问题。

用户对项目的偏好表述了用户在项目属性维度上的兴趣爱好，相比于传统的用户-项目评分矩阵，更能够体现出用户对项目的偏好。在数据集比较稀疏时，传统的用户-项目评分矩阵中含有的数值0更多，不能精确地体现用户的偏好；而在用户-项目属性矩阵中，即使用户对此项目没有评分，但是从项目所属类型上也可以反映用户对此项目的偏好，可以较好地缓解数据稀疏性，提高推荐的精确度。

1.3 时间影响函数构建

人们的兴趣爱好不是一成不变的，用户兴趣会随着时间发生改变，因此，时间变化会对预测结果产生影响。许多学者对时间因素进行了研究，因此衡量时间变化的曲线有很多，最早的遗忘曲线是艾宾浩斯遗忘曲线，如图1所示。该条曲线能够体现出人的记忆随着时间变化的遗忘程度。其数学公式如下所示：

(12)

其中，b表示记忆内容保存量，t为时间间隔，c和k为常数，c=1.25，k=1.84。

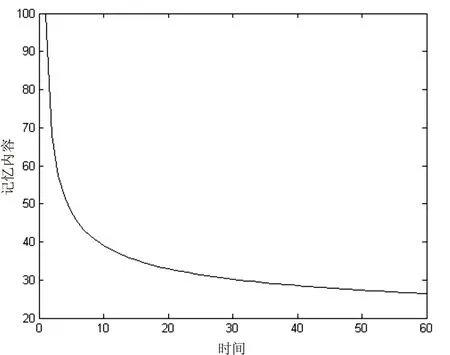
图1 遗忘曲线

从图1可以看出，用户的遗忘程度随着时间的推移先快后慢，是一种非线性的函数。Ding等人[15]于2005年首次根据遗忘曲线提出时间加权函数f(t)，用来表述时间不同，产生的结果也不相同。时间加权函数f(t)的计算公式如下：

f(t)=e-αt

(13)

其中，f(t)的取值范围为(0,1]，参数α控制信息的衰减程度。

在推荐算法中，用户对项目的兴趣会随着时间的变化而变化，而根据前人的研究可知，用户对项目的兴趣变化规律符合遗忘曲线的变化规律，因此可以根据遗忘曲线来拟合时间衰减函数。

该文所使用的时间衰减函数在式(13)的基础上进行改进，用户的兴趣爱好会随着时间在改变，用户在购买某种商品时，更倾向购买与他近期兴趣爱好相似的物品，对久远的物品可能兴趣度较低，时间越近越能反映用户当前的兴趣爱好。但是在最近较短的一段时间段内，用户的兴趣爱好变化程度较小，往往可以认为用户在此时间段内兴趣爱好是相同的，同样在这段时间内用户兴趣的衰减程度是一样的。于是，将用户评分时间分为一个个时间段，每一个时间段代表一个时间窗口T，引入时间窗口来修正时间衰减函数，公式如下所示：

(14)

其中，tui表示用户u对项目i的评分时间；t0表示用户u最初开始评分时间；T表示时间保持周期即时间窗口。利用时间衰减函数对原始评级矩阵进行处理，解决了原始评级的时效性问题。

1.4 改进的加权slope one算法

传统加权slope one算法是通过计算项目间评分差异值，再根据评分差异值以及用户的历史评分来预测用户对未评分项目的评分，没有考虑用户以及项目对预测结果的影响，因此该文对加权slope one算法进行改进。

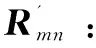
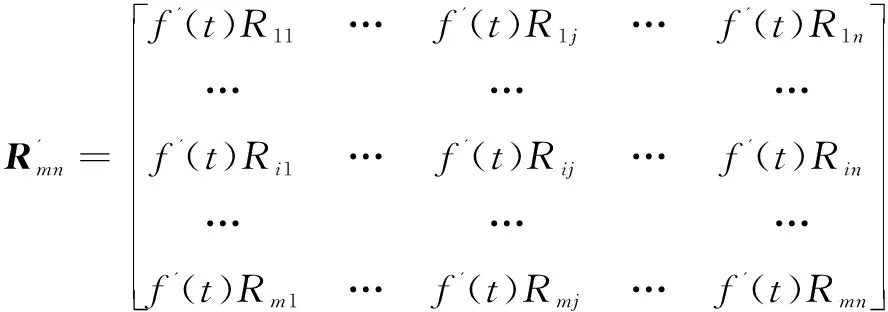
(15)

在新的加权评分矩阵中，f'(t)Rij为用户i对项目j的时间加权评分值，相比于原始的评分矩阵，添加了时间因素更能够体现用户的兴趣随时间是动态变化的。根据新的加权评分矩阵计算用户对项目类型的偏好值，从而获得用户对项目的偏好度，将用户对项目的偏好度构建成用户-属性兴趣矩阵，如式(10)所示。

在填充的用户-项目评分数据下，用户相似度使用皮尔逊相关系数进行计算，皮尔逊相似度计算公式如下：

Simpcc(u,v)=

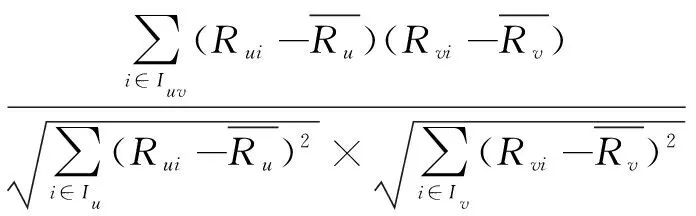
(16)

当用户共同评分数量很少甚至没有时，此时新构建的用户-属性兴趣矩阵Pmk相比原始用户-项目评分矩阵Rmn更能够体现用户间的相似度，因此在新构建的用户-属性兴趣矩阵Pmk中，使用余弦相似度计算用户间相似度，计算公式如下：

(17)

其中，Puv表示属于同一属性类型的用户数量；Pui表示用户u对属性类型i的偏好值；Pvi表示用户v对属性类型i的偏好值。

将式(16)和式(17)计算出的用户相似度通过参数λ进行融合得到最终的用户相似度，公式如下：

Sim(u,v)=λSimpcc(u,v)+(1-λ)Simpu(u,v)

(18)

由式(18)中获得的最终用户相似度，选取前K个相似度作为目标用户的邻居，再根据邻居对目标项目的评分预测用户对目标项目的评分。原始的加权slope one预测公式如下：

(19)

在式(19)的基础上，该文考虑时间对预测结果的影响，从而用时间衰减函数优化预测评分公式，新的预测公式如下：

(20)

1.5 算法描述

算法详细步骤如下：

输入：用户-项目评分矩阵Rmn，邻居数K。

输出：目标用户u对项目i的预测评分。

步骤1：创建用户-项目评分矩阵Rmn，项目-属性矩阵Tnk，时间衰减函数f'(t)，并根据给定的数据集填充矩阵Rmn，Tnk。

步骤2：根据评分矩阵Rmn，使用式(2)计算用户对项目的平均评分。

步骤3：根据项目-属性矩阵Tnk，使用式(5)、式(6)分别计算用户u对项目属性偏好以及高频率属性所占全部属性的权重，并用权重优化项目属性矩阵，即通过式(8)得到加权项目-属性矩阵。

步骤4：根据用户对项目属性偏好值以及加权项目-属性矩阵，使用式(9)计算用户u对项目i的偏好值，并结合平均评分来填充用户对项目未评分矩阵。

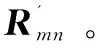
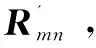
步骤7：由步骤4得出的填充矩阵，使用式(16)计算用户相似度；在矩阵Pmk中，使用式(17)计算用户相似度，将两个相似度通过式(18)进行融合得到最终用户相似度。

步骤8：根据步骤7得到的最终用户相似度，将相似度进行降序排列再选择前K个作为用户邻居，放入邻居集合S(K)中。

步骤9：由步骤8的邻居集合S(K)，根据最近邻居用户对未知项目的评分来预测目标用户对项目的评分，最后再将步骤1中的时间衰减函数f'(t)加入到预测公式中，最后使用式(20)预测出最终目标用户对项目的评分。

流程如图2所示。

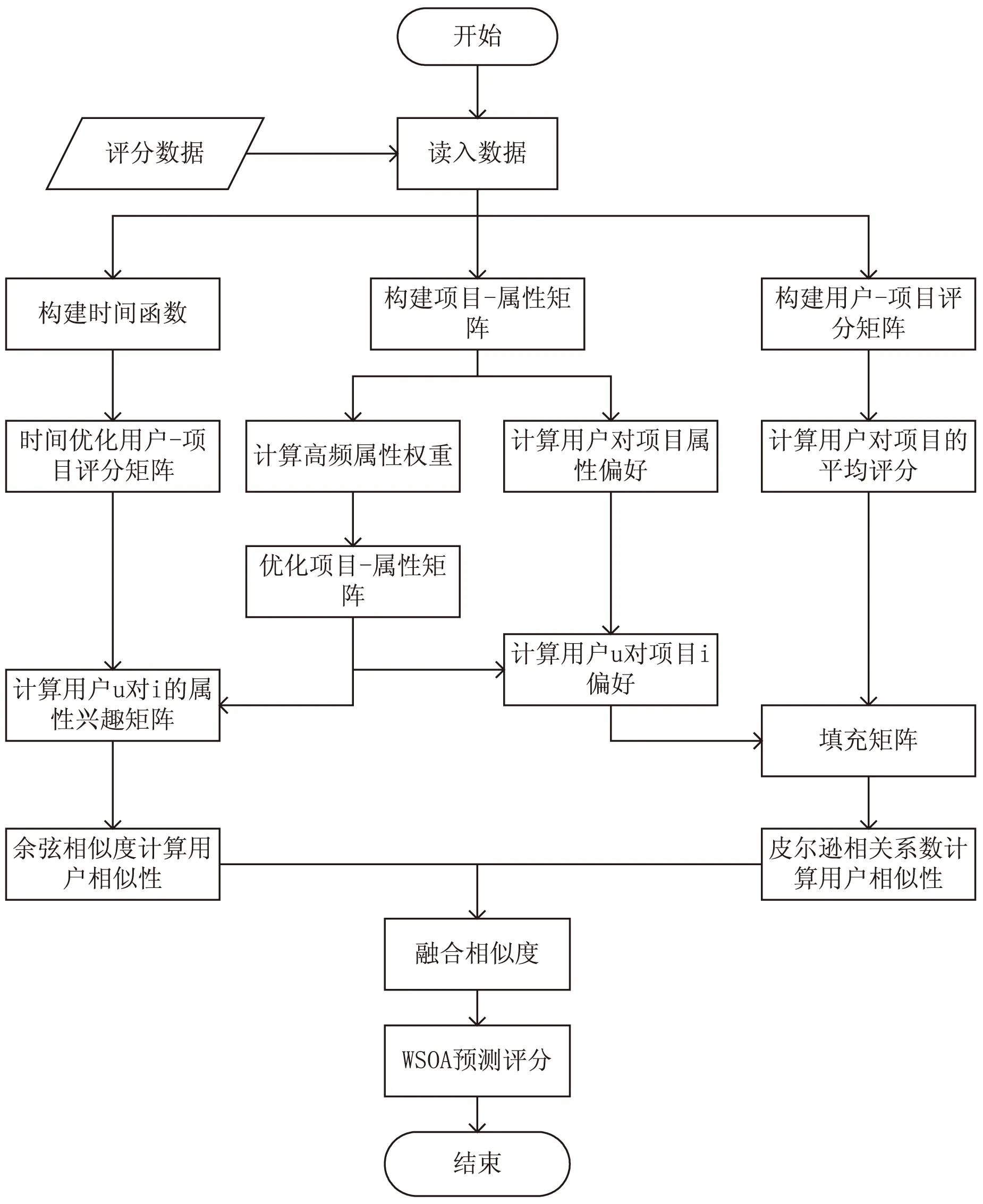
图2 算法流程

2 实验环境及评估指标

2.1 实验环境

本实验在win7 64位操作系统下进行，开发使用的工具是Matlab2014a。

2.2 实验数据集

本次实验所使用数据集是Movielens100K数据集，此数据集是由美国明尼苏大学GroupLens项目组提供。用户对电影评分范围为1～5分，评分越高表明用户对电影越喜爱，反之，则表明用户对电影喜爱程度较低。表1和表2列出了部分电影类别评分信息以及用户对电影的评分信息。

表1 部分电影信息示例

本次实验将数据集按比例8∶2随机划分为训练集和测试集，根据训练集中的数据通过预测公式预测用户对未评分项目的评分，然后再与测试集中的评分数据进行比较，当误差达到最小时，此时的预测效果最好，采用五折交叉验证法进行验证。

表2 部分用户对电影评分时间信息

2.3 评估指标

为验证该算法的预测效果，采用平均绝对误差(mean absolute error，MAE)和均方根误差(root mean square error，RMSE)来衡量。

(21)

(22)

其中，Pi为预测评分，Ti为测试集中实际评分，N为测试集中评分的总数。

3 实验结果与分析

3.1 确定参数λ、K最优值

在填充评分矩阵中计算用户相似度时，使用皮尔逊相关系数计算用户间相似度；当共同评分较少或者没有时，在属性兴趣特征矩阵中，使用余弦相似度计算用户相似度，将两种不同数据集中计算的相似度通过参数λ进行融合。将λ设置为[0.1，0.9]，步长为0.1，邻居数K设置为[100，500]，步长为100进行实验，从而确定参数λ以及K的最优值。实验结果如图3所示。

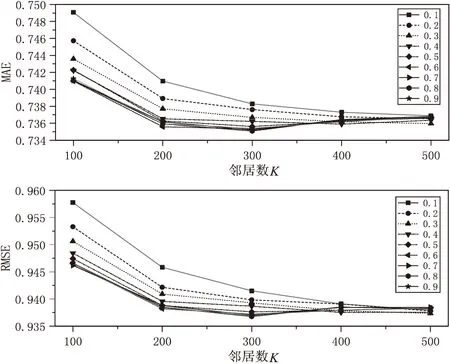
图3 不同参数λ、K对预测结果的影响

从图3可以看出，在不同邻居数K和不同参数λ下，其预测结果也是不相同的。在邻居数K为300时，MAE和RMSE值达到最低，再根据邻居数K为300，寻找一个最优参数λ。从图中可以看出，在邻居数K为300，参数λ取值为0.8时，此时的MAE和RMSE达到最小值。因此，该文在相似度融合时将参数λ设为0.8，邻居数K设为300，基于设置的最优参数进行下面实验。

3.2 实验结果对比与分析

3.2.1 填充评分矩阵与未填充评分矩阵实验对比

针对用户-项目评分矩阵稀疏性问题，提出一种基于改进的填充评分矩阵方法的加权slope one算法(FWSOA)。通过用户对项目平均评分以及用户对项目偏好来填充用户对项目未评分数据，利用填充评分矩阵计算用户相似度，再通过加权slope one算法预测。原始未填充评分矩阵在相似度计算时使用皮尔逊相关系数计算相似度，然后利用加权slope one算法预测。在MovieLens100K数据集进行实验，实验结果如图4所示。

图4 填充矩阵与原始矩阵的MAE和RMSE对比

从图4可以看出，随着邻居数量的不断增大，使用填充数据集进行预测的效果要好于使用原始评分数据集的预测效果，因此填充用户-项目评分矩阵可以有效缓解数据稀疏问题。

3.2.2 时间修正评分矩阵与未用时间优化评分矩阵实验对比

用户兴趣爱好随着时间会发生动态变化，因此提出一种用时间修正评分的加权slope one算法(TWSOA)。该算法使用时间函数修正原始用户-项目评分矩阵得到加权时间评分矩阵，在新的评分矩阵下，计算用户对项目属性兴趣爱好并根据兴趣爱好用余弦相似度计算用户相似度；在原始评分矩阵下通过皮尔逊相关系数计算用户相似度，将计算的两个相似度通过参数λ相结合得到最终用户相似度。相比于单独使用皮尔逊相关系数计算相似度，融合相似度可以有效缓解在共同评分很少甚至没有时数据稀疏性问题。在得出的融合相似度下，选择相近的前K个作为用户邻居集，再根据邻居用户使用加权slope one算法进行评分预测，在预测评分时，引入时间函数优化预测评分公式。将TWSOA算法与未用时间修正的算法(WSOA)进行对比，实验结果如图5所示。

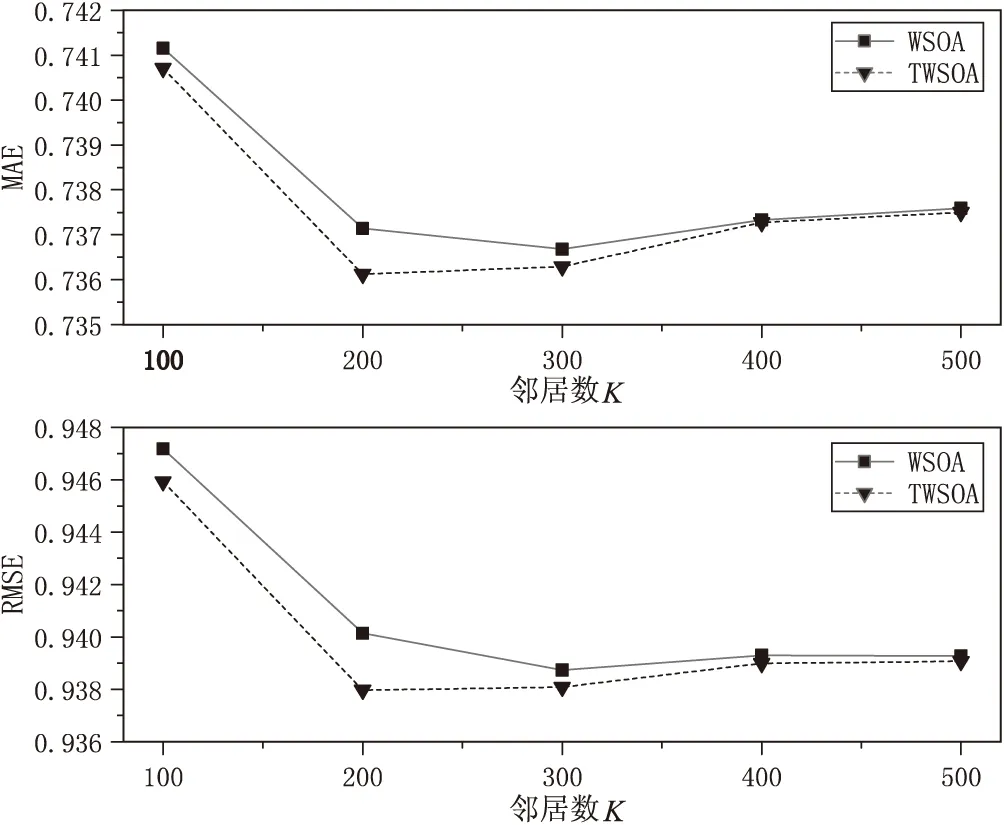
图5 TWSOA算法和WSOA算法与MAE和RMSE关系

从图5可以看出，使用时间优化的评分矩阵进行预测时，其预测误差相比于原始评分矩阵小，因此，用时间修正评分矩阵不仅可以反映用户兴趣爱好随时间是动态变化的，同时在预测评分时也可以提高预测精度。

3.2.3 不同算法实验对比

由上述可知，实验参数λ设置为0.8进行如下实验，将该文提出的FTWSOA算法、FWSOA算法、TWSOA算法与文献[16]中基于加权slope one和用户协同过滤的推荐算法(CF_WSOA)进行对比，实验结果如图6所示。

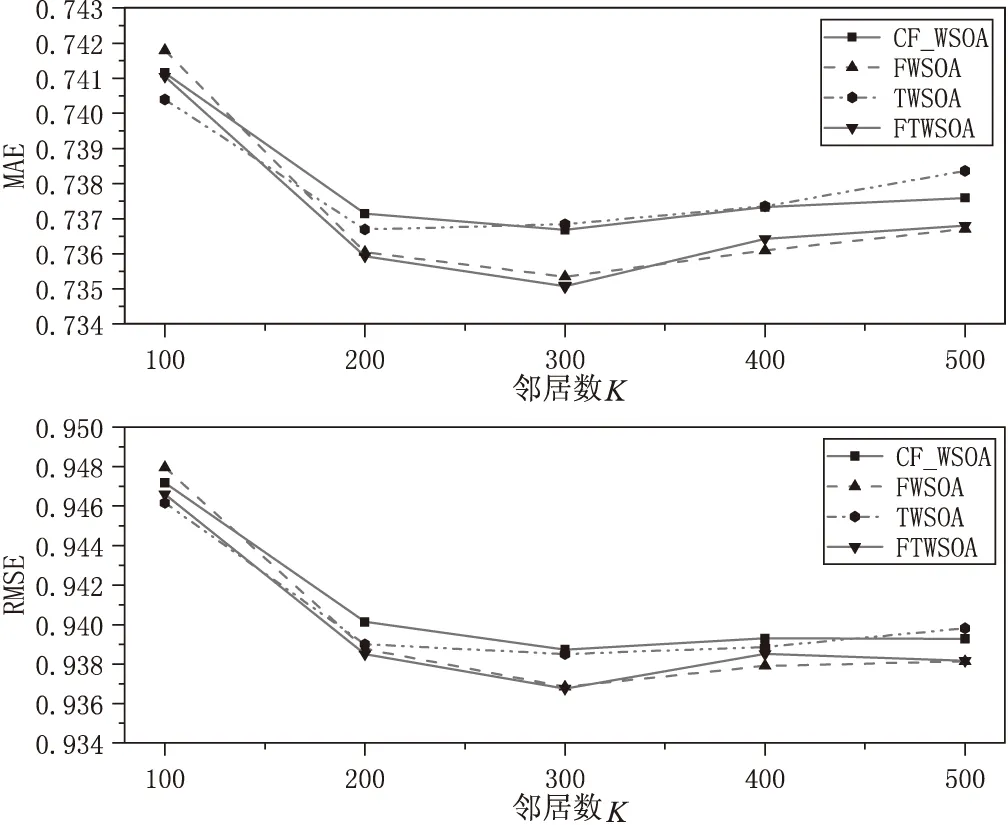
图6 不同算法实验对比

从图6可以看出，该文提出的算法相比于原始的基于加权slope one和用户协同过滤的推荐算法(CF_WSOA)，预测效果均有所提高。在邻居数为100时，使用时间优化的加权slope one算法(TWSOA)误差比较小，随着邻居数的不断增多，使用填充评分矩阵以及时间加权的加权slope one算法(FTWSOA)误差较小；在邻居数K取值为300时，使用FTWSOA算法预测效果达到最优；随着邻居数K继续增大，使用填充评分矩阵的加权slope one算法(FWSOA)的效果相比于其他算法效果更好。

3.2.4 使用五折交叉验证法实验对比

基于参数λ为0.8，邻居数K为300进行实验，将提出的FTWSOA算法、FWSOA算法、TWSOA算法与文献[16]中基于加权slope one和用户协同过滤的推荐算法(CF_WSOA)进行对比，使用五折交叉验证法验证不同算法的结果，实验结果如图7所示。

从图7可以看出，提出的算法的MAE和RMSE均小于文献[16]中的CF_WSOA算法。

图7 不同算法结果对比

4 结束语

通过填充评分矩阵下的加权slope one算法(FWSOA)与原始评分矩阵下的加权slope one算法对比，发现FWSOA的效果优于原始的算法；将使用时间优化的加权slope one算法(TWSOA)与未使用时间优化的算法(WSOA)进行对比，结果显示TWSOA算法优于WSOA算法；最后，将提出的FTWSOA算法、FWSOA算法、TWSOA算法与其他算法CF_WSOA算法进行对比，在MovieLens100K数据集上进行实验，结果表明该算法相比于其他算法在MAE和RMSE上均有所减小。