基于权重学习的高维多目标进化算法
2021-01-19李杭涓崔志华谢丽萍
李杭涓,崔志华,谢丽萍
(太原科技大学 计算机科学与技术学院,山西 太原 030024)
0 引 言
随着社会对生产需求的增长,现实生活中的多目标优化问题[1-2]变得越来越复杂,需要考虑的目标问题也越来越多。因此,当前现有的进化算法[3]在求解多目标优化问题时面临着许多挑战[4-6]。例如,种群进化方向的盲目性,支配关系的无效性,收敛性和多样性不平衡性,真实解决方案集的可视化难度等。
随着目标数量的增多,种群中的非支配解在可行解中的比例会爆炸性地增加[7],促使种群进化的选择压力下降[8-9],导致了支配关系无效。针对这一问题,一些学者试图通过改变支配关系来增加选择压力,这意味着使用新的支配关系来增加进化种群的选择压力。例如,r支配[10]、ε支配[11]等支配关系。虽然在特定的情况下这些支配关系可以选出收敛性强的个体以维持种群的多样性和收敛性,但在此类方法中涉及到参数的取值,具有很大的不确定性。
由于支配关系的无效性,基于密度的多样性维护策略[12]是维持种群进化选择压力的另一方法。例如Deb等[13]提出的NSGA-III,该方法基于参考点选择个体以保持种群的良好分布。但是,该算法在环境选择阶段过于依赖多样性保护机制,收敛信息没有得到充分利用。同时,由于进化算法中进化策略的随机性,使得种群个体进化方向存在盲目性。
针对以上两个问题,该文提出了WL-NSGAIII算法,即分别从产生候选解和选择候选解两个角度对NSGAIII算法进行改进。在WL-NSGAIII算法的匹配选择阶段,设计了一种基于权重的个体学习策略,为种群个体提供进化方向并增强候选解集的收敛性。同时,在WL-NSGAIII算法的环境选择阶段,利用权重信息对小生境选择策略进行改进,在维持种群多样性的同时提高其收敛性。
1 概 述
1.1 多目标优化问题相关定义
定义1(多目标优化问题):
MinF(x)=(f1(x),f2(x),…,fm(x))T,x∈Ω
(1)
其中,F(x)是m维目标空间中的目标函数,x=(x1,x2,…,xn)T是n维决策空间Ω中的决策变量。
定义2(Pareto支配):
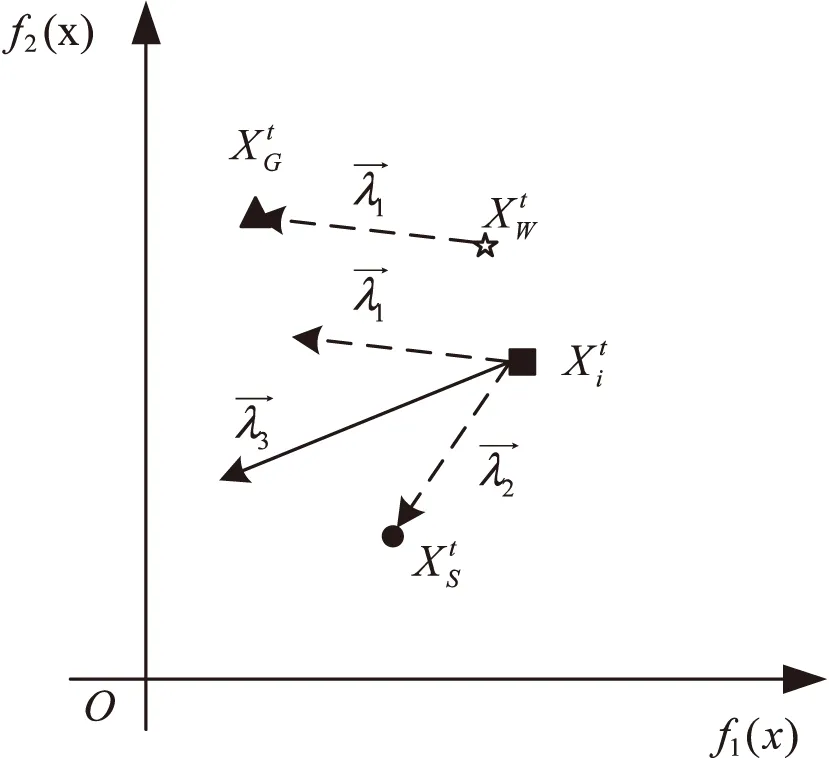
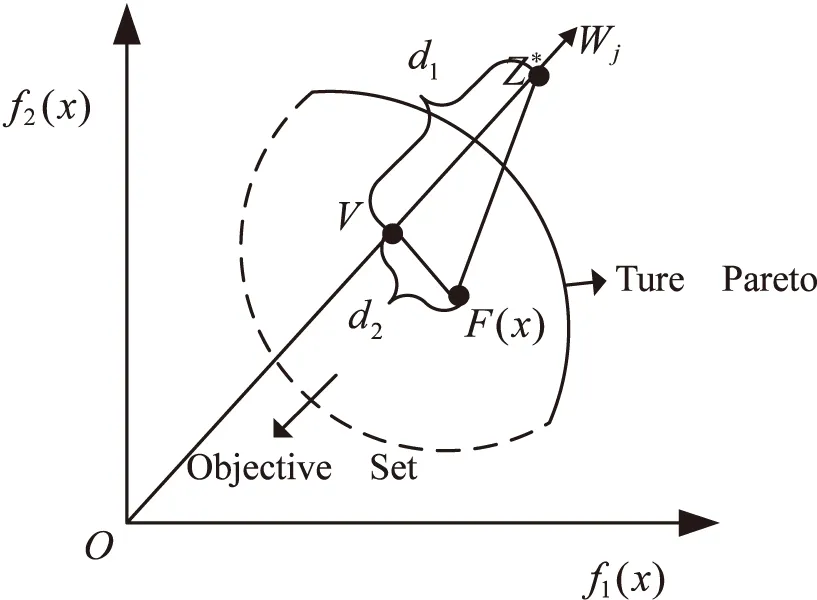
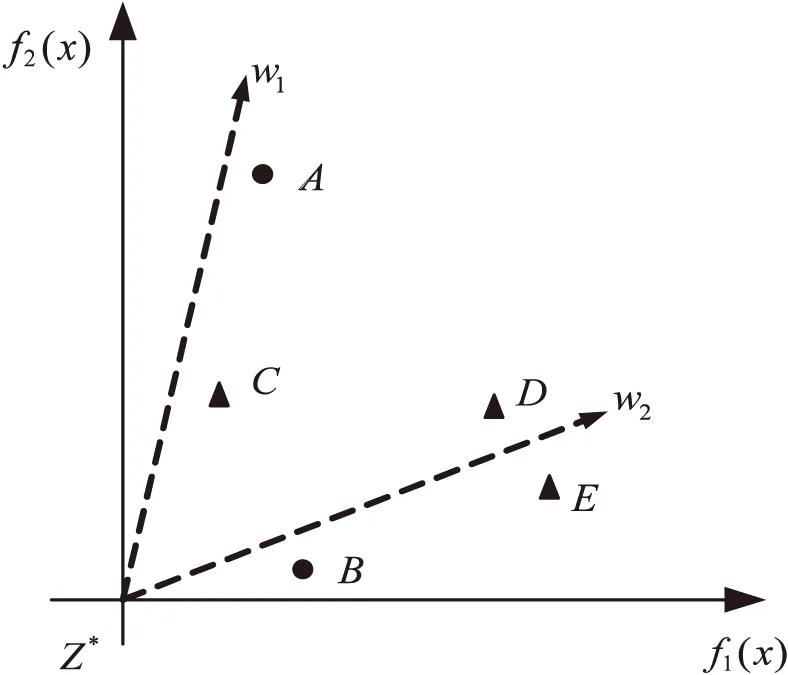
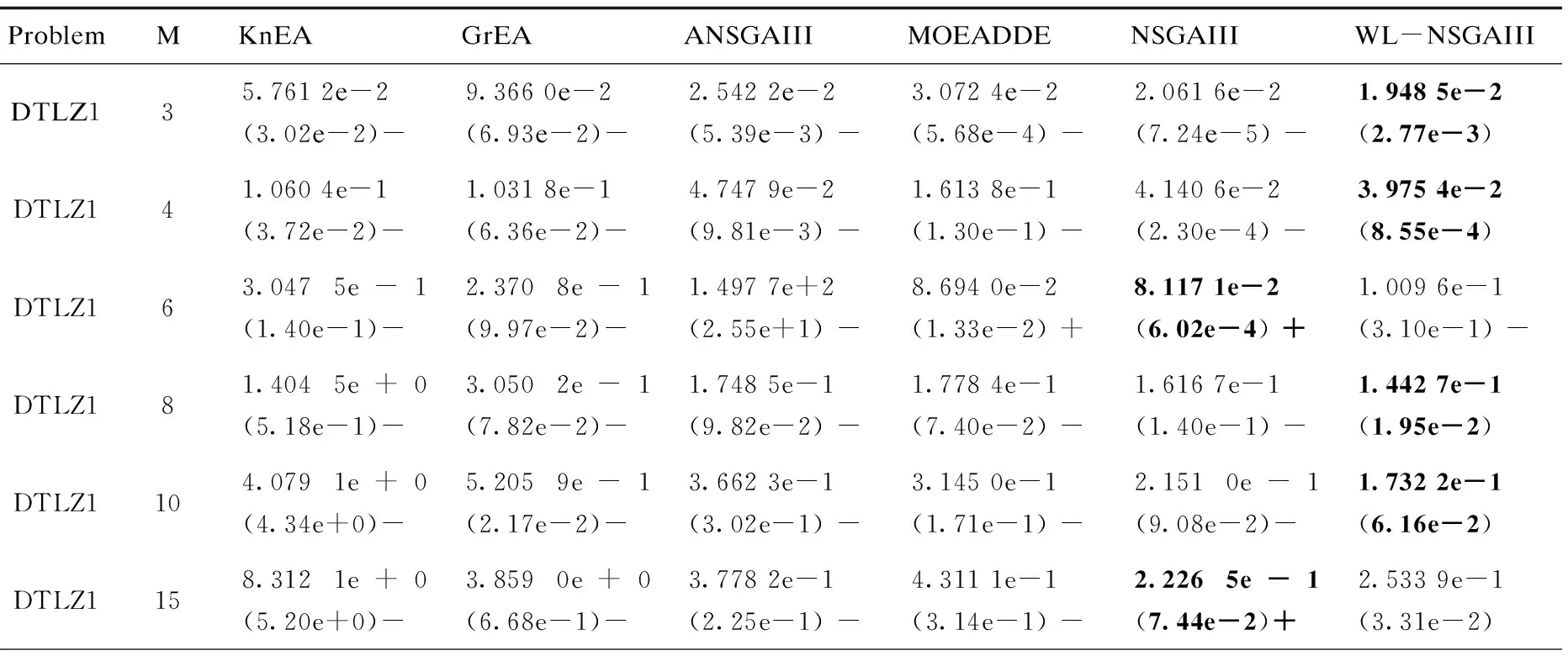
x支配y,记为xy,当且仅当∀i∈{1,2,…,m},fi(x)≤fi(y),∀i∈{1,2,…,m},且∃j∈{1,2,…,m},s.t.fi(x) 定义3(Pareto最优解): 当且仅当一个解x*∈Ω在Ω中x*不会被其他解x所Pareto支配时,x*被称为Pareto最优解。 定义4(Pareto最优解集,PS): 在决策空间Ω中,对于一组给定的最优解集,如果这个集合中的所有解都是Pareto最优解,那么称这个解集为Pareto最优解集。 定义5(Pareto最优前沿,PF): Pareto最优解集中每个Pareto最优解在目标空间中对应的目标函数值向量组成的集合,被称为Pareto最优前沿。 定义6(理想点): NSGAIII算法步骤描述如下: 步骤1:初始化操作。 (2)生成初始种群X={x1,x2,…,xN}T,计算个体pi的目标函数值Fi,i∈{1,2,…,N},N为种群数量; 步骤2:种群进化。 (1)进化操作。父代种群X通过进化操作(锦标赛选择策略,模拟二项式交叉算子,多项式变异算子)产生子代种群Y,并与之合并得到个体数为2N的合并种群R=X∪Y; (3)环境选择。对种群R进行快速非支配排序操作,并利用小生境选择策略对个体进行选择,得到个体数为N的新种群。 步骤3:如果达到最大迭代次数则结束算法;否则执行步骤2。 图1 新个体的进化方向示意图 新的个体更新公式为: (2) (3) 基于权重的个体学习策略的流程如下所示: 第一步:根据式(3),计算子代种群Q中所有个体的T(x)值,并按照T(x)值从小到大排序,排在前m位的个体组成最优集合S={xs1,xs2,…,xsm},排在最后一位的个体作为最差个体; 第三步:从最优集合S中随机选择一个个体作为优秀个体; 在环境选择阶段,NSGAIII算法中的小生境选择策略主要依靠解的分布对个体进行选择,即确定具有最少小生境计数的参考点集,然后选择具有最短d2距离的个体。在这种选择策略下生成的解集虽然有良好的多样性,但由于缺少收敛性,可能远离前沿面。 针对这一问题,该文利用收敛性信息d1对小生境选择策略进行了改进。其中,d1,d2如图2所示,d1是F(x)-Z*在参考点向量w上的投影,被用来评价个体x的收敛性;d2是一种衡量种群多样性的方法。 图2 收敛性与多样性关系示意图 在原有的小生境选择策略中,如果同时存在多个参考点集则随机选择一个参考点,然后依赖个体的多样性信息进行相关的选择操作。在此过程中可考虑加入个体的收敛性信息,以平衡种群的多样性和收敛性,即如果同时存在多个参考点集则根据个体的收敛性信息进行选择。 图3 参考向量所关联的个体 小生境选择改进策略的步骤如下所示: 第一步:将种群中所有个体与距离其最近的参考点进行关联; 第二步:利用式(3)计算最后一层上待选择个体的适应度值,根据适应度值对个体进行排序,并按顺序记录与个体相关联的参考点; 第三步:判断算法中已选择的个体数是否小于或等于种群个数N。如果没有达到迭代次数或不满足终止条件已选择的个体数小于或等于种群个数N,则进行第四步;如果已选择的个体数大于种群个数N,则输出种群; 第四步:将关联个体数最少的参考点作为一个集合; 第五步:按照第二步中所记录参考点的顺序在第四步中得到的参考点集合进行匹配查找。只要找到一个则立即停止查找并转到第七步;如果查找完毕时,没有找到相对应的参考点,则转到第六步; 第六步:从第四步所得到的集合中随机选取参考点,对其相关联的个体进行判断,如果为待选择个体,则转到第七步;如果为已选择个体,则进行标记并重复第六步; 第七步:选取该个体;转到第三步。 根据2.1和2.2所述操作对NSGAIII算法的改进,WL-NSGAIII算法的基本步骤如下所示: 第一步:初始化操作:生成参考点和理想点、初始化种群; 第二步:判断算法是否达到迭代次数并满足终止条件。如果没有达到迭代次数或不满足终止条件,则进行第三步;如果达到迭代次数并满足终止条件,则终止算法,输出种群; 第三步:通过锦标赛选择算子、模拟两点交叉算子和多项式变异算子进行进化操作,在父代种群的基础上产生子代种群; 第四步:匹配选择阶段,利用基于权重的个体学习策略在子代种群的基础上产生学习种群,将子代种群和学习种群进行个体比较和保留,得到候选种群; 第五步:合并父代种群和候选种群; 第六步:更新理想点; 第七步:环境选择阶段,利用小生境选择改进策略对合并后的种群进行个体选择得到新种群;转到第二步。 该文选择经典的KnEA[14]、GrEA[15]、ANSGAIII[13]、MOEADDE[16]、NSGA-III等算法作为对比算法。 采用常用的综合性指标反世代距离[17](inverted generational distance,IGD)作为评价标准。它主要通过计算每个在真实Pareto前沿面上的点(个体)到算法获取的个体集合之间的最小距离和,来评价算法的收敛性能和分布性能。值越小,算法的综合性能包括收敛性和分布性能越好。 (4) 其中,P为均匀分布在真实Pareto面上的点集,|P|为分布在真实Pareto面上的点集的个体数。Q为算法获取的最优Pareto最优解集。而d(v,Q)为P中个体v到种群Q的最小欧几里得距离。 文中所有算法的种群大小保持一致且不同目标个数的目标函数有各自对应的种群数量,如表1所示。算法的交叉概率均设置为1,变异概率均设置为1/D(D为变量数量);最大评估次数为30 000,算法独立运行30次。 表1 种群参数设置 在模拟实验中,基于3~20个目标的DTLZ1-DTLZ4测试集[18]中的IGD值,将WL-NSGAIII与KnEA、GrEA、ANSGAIII、MOEADDE、NSGA-III进行了比较。实验结果如表2所示,在表中,“+”表示比WL-NSGAIII更好的结果,“=”表示与WL-NSGAIII相似的结果,“-”表示比WL-NSGAIII差的结果。粗体数字表示同一问题的最佳结果。 通过比较6种不同算法的IGD值,可以看出WL-NSGAIII算法在DTLZ1-4测试问题上的整体性能表现良好,尤其是在DTLZ1和DTLZ3测试问题上表现突出。可见,基于权重信息的个体学习策略和小生境选择改进策略,能够在维持种群多样性的基础上,增强其收敛性。 表2 在DTLZ测试集上不同算法的IGD值 续表2 针对种群个体进化的盲目性以及依赖多样性保护机制这两个问题,提出了一种基于权重学习的高维多目标进化算法WL-NSGAIII,分别从产生候选解和选择候选解两个角度对NSGAIII算法进行改进。在算法的匹配选择阶段,通过基于权重的个体学习策略,为种群个体提供进化方向并增强候选解集的收敛性。同时,在算法的环境选择阶段,利用权重信息对小生境选择策略进行改进。最终,在维持种群多样性的同时提高其收敛性。通过模拟实验结果可以看到,WL-NSGAIII算法在处理高维多目标优化问题上性能表现良好。1.2 NSGAIII算法
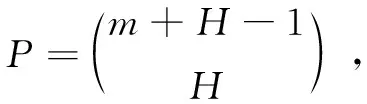
2 WL-NSGAIII算法
2.1 基于权重的个体学习策略

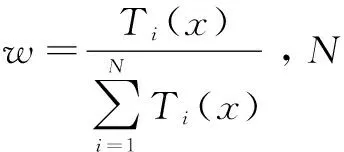
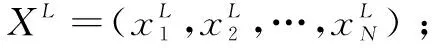
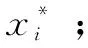
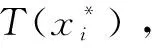
2.2 小生境选择改进策略

2.3 基于权重学习的高维多目标进化算法流程
3 实验与分析
3.1 评价指标
3.2 参数设置

3.3 实验结果与分析

4 结束语
