最优房室模型的药代动力学系统研制及应用

丘陵,黄雄波,刘武萍,廖叶权

作者单位： 528000 广东省佛山市中医院药剂科(丘陵、廖叶权) 528137 广东省佛山市，佛山职业技术学院电子信息学院(黄雄波、刘武萍)

药代动力学是由新兴药学与应用数学之间相互交叉和相互渗透而形成的边缘科学，其重点研究药物进入人体后，相关的各种体液、组织及排泄物的代谢产物水平与时间之间的变化规律[1-4]。药物作为一种异物进入体内后，机体就会动员各种机制使药物发生化学结构的改变，即药物发生代谢转化的过程，而代谢是药物在体内消除的重要途径。药物经代谢后作用往往降低或完全消失，但也有极小量的药物经代谢后药理作用增强。在实际的临床研究和试验中，如何构建合理的数学模型以便精确描述药物血药浓度的变化规律，对新药研发、药物评级及临床合理用药均有重要的现实意义[5-7]。

对药物进行动力学分析，通常是基于某一数学模型对血药浓度序列进行拟合分析，并运用相关的数值计算方法求解对应的参数，进而得到合适的药代动力学模型[8-9]。当前，药物动力学有种类繁多的数学模型，若按照输入和输出的关系进行划分，则分为有线性模型和非线性模型两种；而按照人体机制的原理进行划分，则可分为房室模型和生理模型。此外，房室模型根据房室数量，还可划分为单室模型、双室模型及多室模型。非线性药物动力模型可通过泰勒级数展开的方法实现线性化转换，故本文重点对线性房室模型展开研究。针对现有的药代动力学分析软件存在的不足，为有效提升药物工作者的效能，本文拟研制具有最优房室选择机制的药代动力学分析系统。

1 原理方法

若要准确描述某一药物在人体内的代谢变化过程，可通过在不同的时刻点提取有关的血药浓度样本，并选择合适的模型对该血糖序列样本进行拟合。房室模型只有确定最佳的房室数量，才能准确表征药物的代谢动力学特征。被评价药物是属于单室模型药物、双室模型还是多室模型直接影响拟合模型的精度，因此，最优房室数量的确定尤为重要。

1.1 最优线性房室模型 如式(1)所示，利用线性房室模型对药物进入人体后的血药浓度样本加以描述[10]。

式(1)中，C(t)为t时刻对应的血药浓度数值，j为模型中房室的数量，αi,βi(i=1,2,…j)为各房室对应的指数项参数。

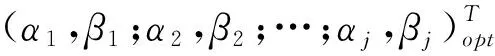
(2)

1.2 系统的设计原理与框图 利用现有的药代动力学分析软件进行血药浓度的建模与分析，需预先初始化模型的房室数量，为了获得最优的线性房室模型，药物工作者往往需进行多次的试探性操作及花费大量无效的计算工作。针对这些不足，拟设计具有最优房室选择机制的药物动力学分析系统。新研制系统主要有两大模块组成：房室模型的预处理和最优模型的参数求解，见图1。具体的原理方法如下。

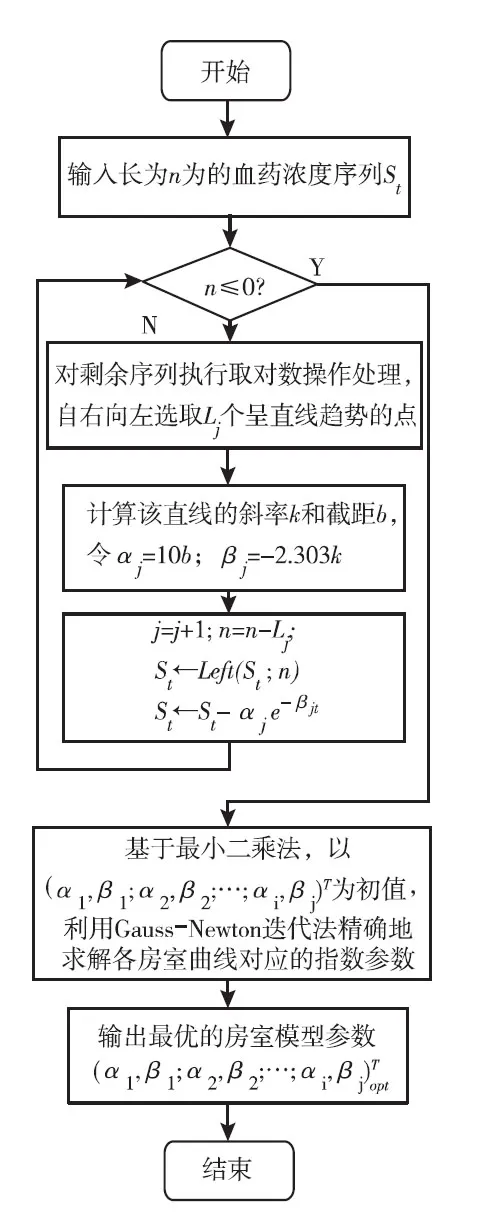
图1 具有最优房室选择机制的药代动力学分析系统的程序流程图

1.2.1 房室模型的预处理：预处理模块用于确定最优线性房室模型的房室数量，在此基础上，析出各房室指数曲线的参数初值。

1.2.1.1 房室分离及求解对应指数曲线的参数初值：根据残数法得知，各房室曲线对应的指数应满足如下关系

β1≥β2≥…≥βj

(3)

联合式(1)和式(3)可知，随着时间的t不断增长，血药浓度中指数数值较大的房室成分便逐渐趋向于零。于是，对血药浓度序列St进行取对数的操作处理，式(4)表明，血药浓度的对数序列[lg(St)]在其末端(t→n)处近似为一条直线。为此，基于某一误差阈值自右向左地选取Lj个呈直线趋势的样本，在此基础上，如式(5)所示求得该直线的斜率k和截距b，便可得到当前被分离房室对应指数曲线的参数初值。

lgS(t)≈lg(α1e-β1t+α2e-β2t+…+αje-βjt)

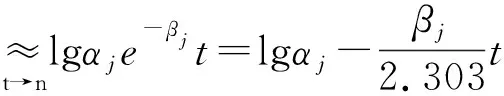
(4)

1.2.1.2 分离并析出残差序列：首先更新序列的样本长度n，然后从已有序列St中删除步骤(1)中已处理的Lj个样本点，即

式(6)的Left(St,n-Lj)为左向分离函数，其功能是从左边首位置起，提取n-Lj个样本点。利用式(7)去掉上一房室成分对序列St的影响，并得到如下的残差序列：

St←St-αje-βjt，t=1,2,…,n-Lj

(7)

增加房室数量j=j+1，重复式(4)～(7)的处理，直至现有序列其样本长度n≤0。最后，得到待分析血药浓度序列的最优房室数量j及其对应的指数曲线的参数初值。

1.2.2 最优模型的参数求解：用对数化分段处理的方式对血药浓度序列进行分离，得到的指数曲线参数仍有一定的误差，为进一步提高拟合精度，设参数向量(α1,β1;α2,β2;…αj,βj)T为X，并定义

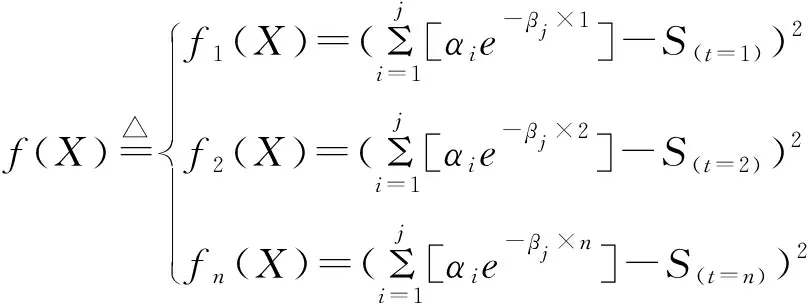
于是，式(2)的极小问题便可化为求解如下的多元函数φ(X)的极小值

(9)

利用Gauss-Newton迭代法求解式(9)，得到相对应的迭代求解表达式为[11-12]

(X)k+1=(X)k-G((X)k)-1g((X)k)

(10)

式(10)中，G(X)和g(X)的定义如下

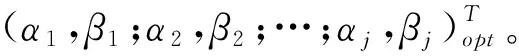
2 实例应用

基于上述的原理分析方法，在Microsoft Visual Studio 2015的C++开发环境中编制具有最优房室选择机制的药代动力学软件分析系统，下面将结合具体实例来说明系统的运行情况。

2.1 数据来源 实验选用的血药浓度序列来源于文献[13]，具体的数值见表1。

表1 某血药浓度的实测序列

2.2 实验结果 在新研制的《基于最优房室模型的药物动力学分析系统》中，首先通过[初始预置]模块设置“误差阈值”≤10%、“直线趋势的最小样本数”为3，然后单击系统工具栏中的[数据导入]、[房室分离]及[迭代求解]等操作按钮，得到计算结果。见图2。

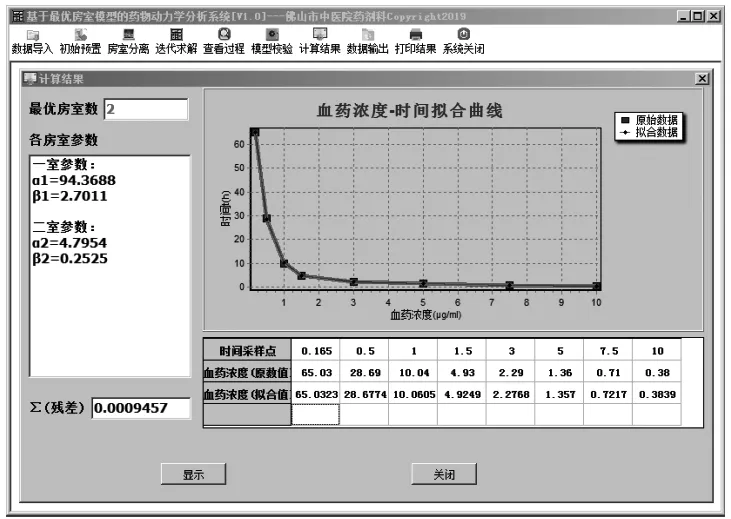
图2 最优房室模型的药物动力学分析系统的计算结果示例

在图2中，系统自动计算出表1对应的血药浓度序列其最优房室数量为2，与文献[13]的结论一致。较现有的药代动力学分析系统而言，由于本系统无需用户预置所需的房室数量，从而有效提高系统的易用性。此外，在模型参数的迭代求解过程中，通过增加求解参数的位数字长，系统得到的拟合精度优于文献[13]的结果。

3 分析与讨论

3.1 结果分析 以表1的血药浓度序列为例，单击图3的[查看过程]按钮，系统将图文并茂地显示建模分析的过程数据。其中，“房室模型的预处理过程”面板里有被处理的血浓序列原值、对数处理后的序列值及相邻两点的斜率计算结果；而“房室模型的参数迭代求解过程”面板则显示各次迭代所得的参数值以及对应的迭代误差。

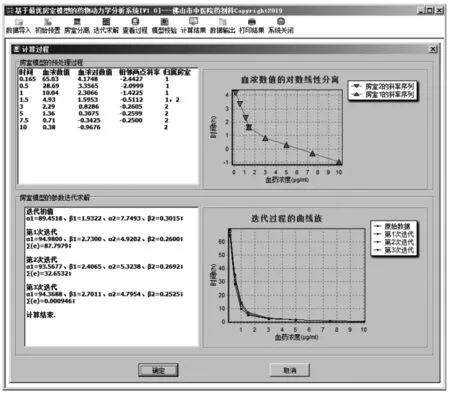
图3 最优房室模型的药物动力学分析系统的计算过程示意图

在图3中，系统根据斜率的不同数量等级自右向左地对血浓序列进行房室划分。由于

不难发现，斜率序列的数量等级在(-0.5112,-1.4225)之间发生跳变，转折点为“-0.5112”，所以系统便析出最佳的房室数为2，其对应的斜率子序列分别为{-0.25，-0.2599，-0.2605，-0.5112}和{-0.5112，-1.4225，-2.0999，-2.4427}。

分别利用上述子序列的首尾元素对应的时间值及血浓对数值{(0.165，4.1748),(1.5，1.5953)}、{(1.5，1.5953),( 7.5，-0.3425)}构造两个直线方程，即

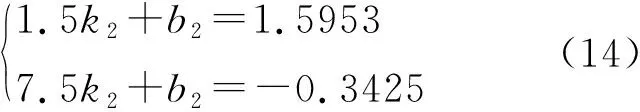
解上述方程组，有(k1=-1.9322,b1=4.4936)和(k2=-0.3229,b2=2.0798)，在此基础上，系统将方程组的解代入式(5)，得到如图3所示的两个房室参数的迭代初值(α1=89.4518,β1=1.9322)和(α2=7.7493,β2=0.3015)。

基于已求出的房室数量和迭代初值，系统利用Gauss-Newton迭代法对表1的血药浓度序列进行最优模型参数求解。从图3可知，系统在拟合误差1×10-4的迭代结束条件下，进行了3次迭代求解后获得相应的计算结果；从迭代过程的数值和曲线族看，系统具有良好的算法收敛性。

3.2 模型检验 拟运用F检验法[14-15]对上述的房室模型进行有效性的确认。

3.2.1F检验法的检验过程：F检验法的检验过程主要分为如下两步：

3.2.1.1 计算各房室模型的F值：不同房室数量的拟合模型，其F检验值可用下式进行计算

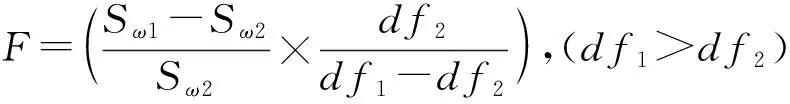
(15)

式(15)中，Sω1和Sω2分别为相邻两种房室数量的拟合模型的残差平方和；df为自由度，其值等于实验样本点的长度减去参数的数目。如表1的血药浓度序列的样本长度为8，且单室、双室及三室模型的参数数目分别为2、4和6，于是该序列对应的单室、双室及三室模型的df分别为6、4和2。

3.2.1.2 模型的F检验：若当前房室模型的F值比相应自由度的F界值(5%显著水平)大，便可认为将拟合模型的房室数量增1是有意义的；否则，房室数量应选择较小的那个房室数。

3.2.2 新模型的F检验法：运用式(15)计算新研制系统求得的各房室模型的F值，并按照P<0.05的显著性水平查F界值表，得到表2所示的结果。

表2 新研制系统求得的各房室模型的值

从表2的数据得知，由于46.42>6.94，说明拟合模型从单室增加到双室是有意义的；又由于2.19<4.53，按照模型参数的最小化原则，拟合模型的房室数量未增至为三室。

综上所述，通过对新研制系统的房室模型进行F检验，得出的最优房室数量为2是正确和可信的。

4 小 结

本文基于残数法和Gauss-Newton迭代法，采用Microsoft Visual Studio 2015的C++编程语言，构建了一个具有最优房室选择机制的药代动力学软件分析系统，由于系统能自动析出待分析血浓序列的最佳房室数量，并求出更精确的房室模型参数，所以新研制的系统可有效提高药物工作者的效能，具有一定的应用推广价值。