有轨电车客运通行能力计算方法

黎冬平

（1.上海市城市建设设计研究总院（集团）有限公司，上海 200125；2.上海有轨电车工程技术研究中心，上海 200125）

0 引言

随着公交优先发展战略的推进及人们对于公交出行品质和环境的重视，有轨电车由于节能环保、快捷舒适、投资较低等特征在国内多地得以应用，处于稳步发展阶段。有轨电车运行时，平面交叉口是影响其客运通行能力的主要因素。研究有轨电车客运通行能力与交叉口信号控制间的关系，并提出客运通行能力计算方法，对明确有轨电车适应性、指导线网规划及工程设计具有重要意义。

国内外对于有轨电车规划设计取得了一定的研究成果。国际上，Holmes[1]编制了Edingburgh有轨电车设计手册，提出了工程设计要求；Ham⁃moum[2],Praml[3],Ohmori[4],Annika 等[5]分别针对有轨电车与交叉口路面的相互关系、能耗排放对比、交通安全影响因素等进行了研究；美国公交协作研究计划（Transit Cooperative Research Pro⁃gram,TCRP）报告[6]给出了快速公交系统和轨道交通的通行能力计算模型，但未明确与信号周期时长的关系；Nagatani[7]研究了信号周期对有轨电车行程时间的影响。国内有毛保华等、汪波等[8-9]分别研究了全封闭轨道交通的通行能力计算方法及提升方法；胡少帅等、冯浚等[10-11]基于停靠站的能力分别研究了公交专用道和快速公交系统的通行能力；黎冬平等[12]提出信号协调控制是影响有轨电车客运通行能力的关键因素；周小华等[13]、陶涛[14]、蒋丽华[15]分别研究了全封闭条件下有轨电车三通立交、车站及折返道岔等节点的通行能力。

整体而言，欧洲有轨电车在交叉口以绝对信号优先控制为主，国内已有轨道交通通行能力计算方法主要针对全封闭运行环境，通行能力受交叉口约束小；快速公交系统通行能力的计算方法适用于车辆排队进站且单个周期内可以通行多辆公交车的情形。截至目前，尚缺乏针对既考虑交叉口约束，又属于单站位情形的有轨电车客运通行能力计算方法的研究。为此，本文将基于有轨电车的运行特征，建立有轨电车客运通行能力模型，并计算有轨电车客运通行能力的取值范围，量化分析有轨电车客运能力与交叉口信号控制之间的关系。

1 有轨电车运行特征分析

本研究主要基于有轨电车在国内作为中运量公交方式的定位[16]，其具有以下运行特征：

（1）有轨电车享有专用路权，即路段上拥有专用车道，交叉口采用信号灯控制，运行主要受车站停靠和交叉口信号的影响；

（2）有轨电车客运通行能力的关键影响节点是设置在交叉口的车站，发车间隔需综合考虑车站停靠时间和交叉口等待时间；

（3）有轨电车采用编组运行，车站均为单站位，因此通过交叉口采用“一灯一车”模式，即一个周期同一相位只能通过一辆有轨电车。

鉴于有轨电车目前主要为单条线路，本文主要研究单方向通道的客运通行能力，这是网络客运通行能力研究的基础。同时，由于路面影响因素复杂，本文计算的理论值未考虑外界非正常干扰因素。

2 有轨电车客运通行能力计算方法

2.1 有轨电车客运通行能力的概念

有轨电车客运通行能力是指在一定运行条件下有轨电车单位时间内可运送的最大乘客数，等于线路通行能力与车辆载客容量之积[8]：

式（1） 中：P为有轨电车的客运通行能力（人/h）；T为有轨电车的线路通行能力（car/h）；B为有轨电车的车辆载客容量（人/car）。

2.2 线路通行能力计算模型

2.2.1 线路通行能力基础计算模型

线路通行能力是指单位时间内能通过的有轨电车最大车辆数，即单位时间与最小间隔时间的比值[8]。最小间隔时间受进站清空时间、停站时间的影响，并应留有运营裕量。线路通行能力按下式计算：

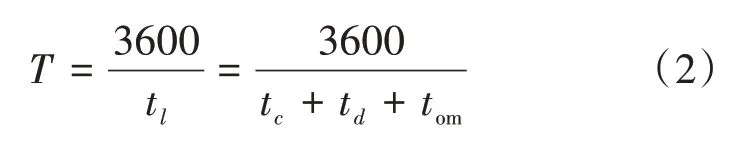
式（2）中：tl为车辆的最小间隔时间（s）；tc为进站清空时间（s）；td为平均停站时间（s）；tom为运营裕量（s）；T意义同前。

（1）进站清空时间

进站清空时间是指站台等待一辆有轨电车完全驶离且与站台末端保持一定安全距离的时间，其计算可借鉴轨道交通中关于车站处移动闭塞安全间隔时间的计算方法[6]：

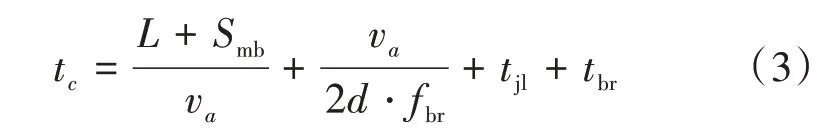
式（3）中：L为车辆长度（m）；Smb为清空时后车距车站末端的最小安全距离（m）；va为车辆进站速度（m/s）；fbr为安全制动系数，常取75%；d为减速度（m/s2）；tjl为由于紧急制动而导致的时间损失，常取0.5s；tbr为制动系统反应时间，常取1.5s；tc意义同前。

取Smb=10m,va=4m/s,d=2.8m/s2，分别计算不同车辆长度下的进站清空时间，结果如图1所示。可见，进站清空时间对于单辆车（车长33～37m），可取15s；对于重连车辆（车长66～74m），可取23s。

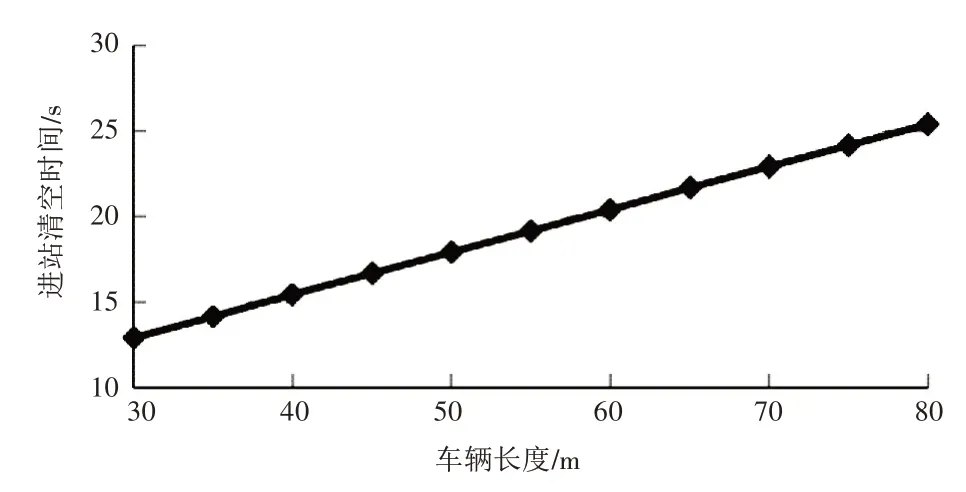
图1 不同车辆长度下的进站清空时间

（2）停站时间

有轨电车的停站时间受车辆开门速度、车长等因素影响，同时与乘客乘降量的波动有关。停站时间波动性对线路通行能力的影响用停站时间波动系数τv表示。停站时间波动系数是有轨电车停站时间与平均停站时间比值的标准差，通常在0.4～0.8之间取值。当τv=0时，表示有轨电车在所有车站的停站时间相同；当τv=1.0 时，停站时间的标准差与停站时间的均值相同。

（3）运营裕量

在停站时间和进站清空时间中加入运营裕量以确保有轨电车的进站失败率不超过期望值。有轨电车为单站位系统，应将进站失败率控制在较低水平。当停站时间服从正态分布时，运营裕量按下式计算：

式（4）中：tom,τv,td意义同前；Z为满足期望进站失败率的标准正态变量，不同进站失败率对应的Z值如表1所示。

表1 不同进站失败率对应的Z值

2.2.2 不考虑交叉口影响的线路通行能力

若不考虑交叉口影响，将进站失败率控制在2.0%以下时，根据式（2）～式（4）可计算得到有轨电车单辆车与重连编组下的线路通行能力，结果如表2和图2所示。

表2 不考虑交叉口影响下有轨电车线路通行能力

从图2 可知，在不考虑交叉口影响下，平均停站时间越长，线路通行能力越低。按照国内有轨电车设计参数，单辆有轨电车停站时间取25s时，线路通行能力可达47car/h；重连有轨电车需要更长停站时间，常取30s，线路通行能力可达37car/h。

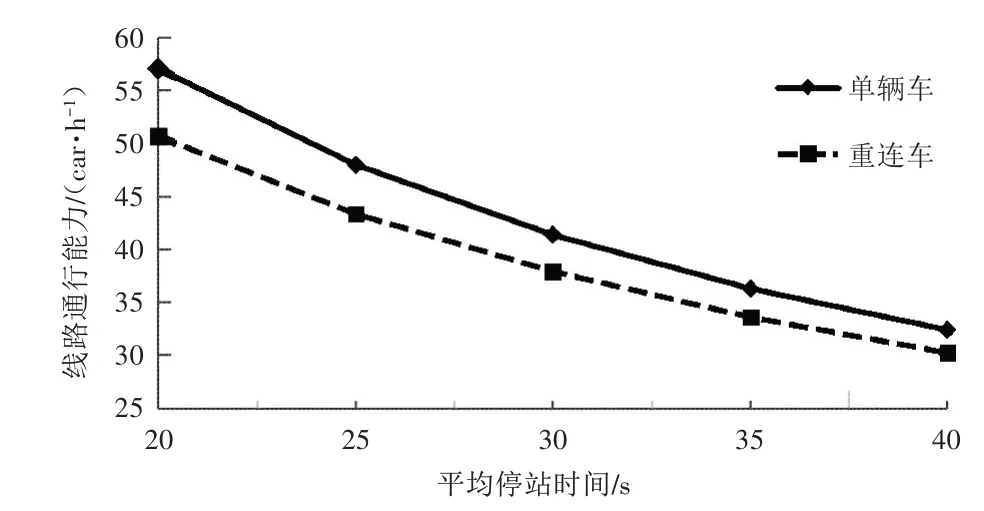
图2 不同平均停站时间下的有轨电车线路通行能力

当有轨电车在交叉口能实现绝对信号优先时，可看作享有全封闭路权，线路通行能力主要受平均停站时间影响，与交叉口的信号周期和配时无关，取值如表2所示。

2.2.3 无信号协调下的线路通行能力

当交叉口无信号协调控制时，认为有轨电车随机到达交叉口，最不利节点是设有车站的交叉口，最大的停站时间可能是车站上下客时间与之后等待红灯时间之和。由于车辆在交叉口等待红灯的时间也是随机的，此时将车辆平均停站时间与在交叉口红灯平均时间之和变换为交叉口平均停站时间：

式（5）中：tdr为交叉口平均等待时间（s）；td意义同前；tr为车辆在交叉口的红灯平均等待时间（s），可按下式计算：

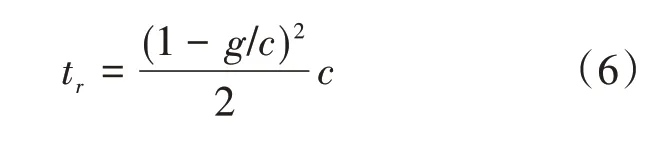
式（6）中：g/c为有轨电车线路通行相位的绿信比；c为交叉口信号周期时长（s）。由该式可知，绿信比g/c越大，tr越小；信号周期时长c越长，tr越大。

将式（5）、式（6）代入式（2），当进站清空时间和运营裕量在一般情形下取值时，计算不同信号周期时长和绿信比下的有轨电车线路通行能力，结果如表3、图3～图4所示。

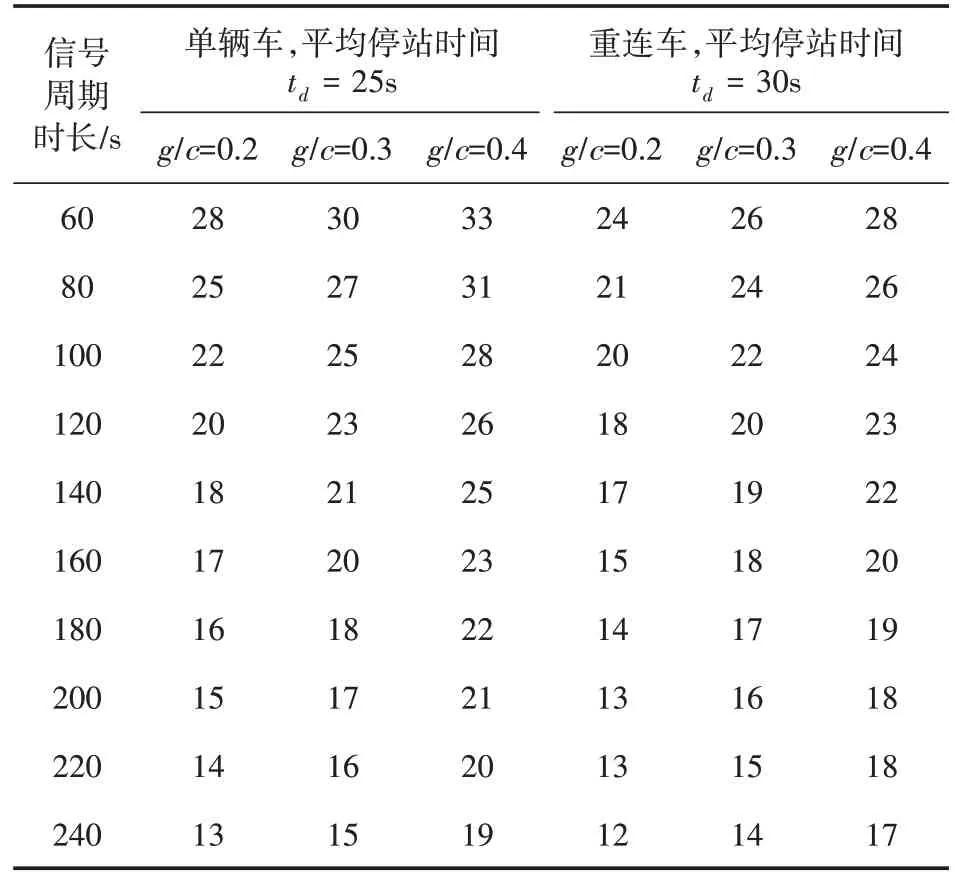
表3 信号控制交叉口下的有轨电车线路通行能力

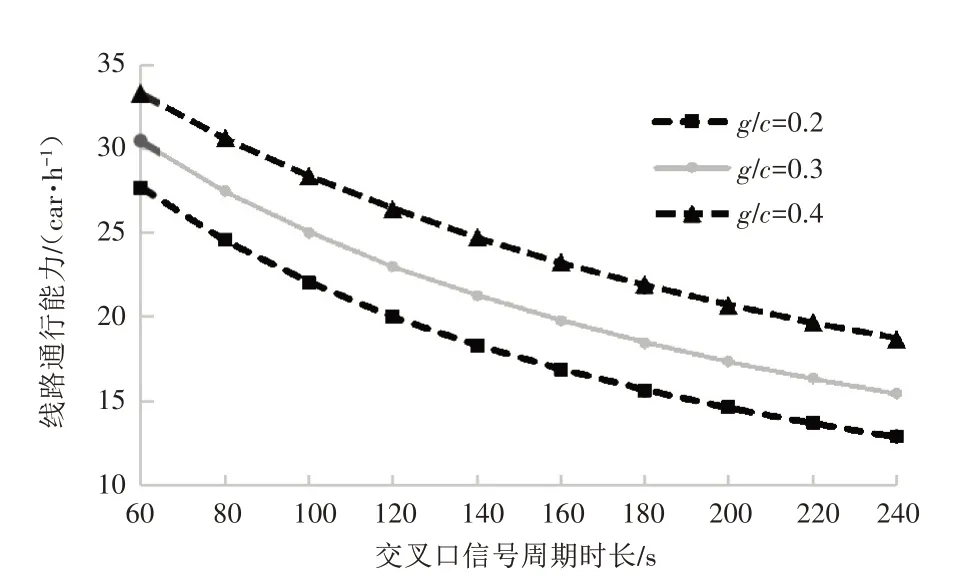
图3 单辆车下不同信号周期的线路通行能力（td=25s）

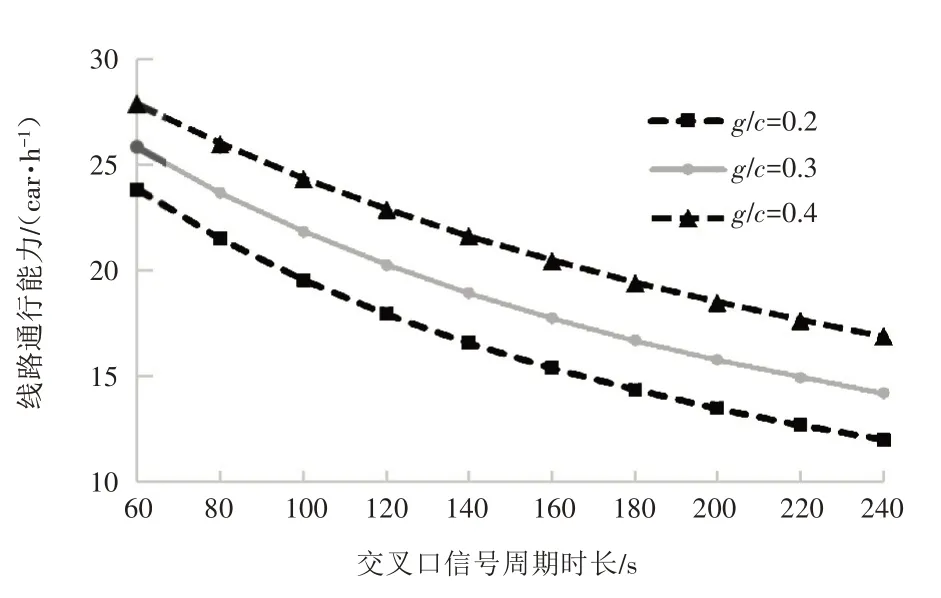
图4 重连车下不同信号周期的线路通行能力（td=30s）

从表3、图3～图4 可以看出，交叉口信号周期越长，线路通行能力越低；绿信比越低，线路通行能力越低；车辆越长，线路通行能力越低。在2min 的信号周期下，交叉口信号无协调控制时，单辆车的线路通行能力为23car/h，而重连车的线路通行能力为20car/h。

2.2.4 信号协调控制下的线路通行能力

在发车间隔与信号周期协调控制下，可以使有轨电车在满足停站时间要求的同时缩短交叉口等红灯的时间。当有轨电车与信号控制采用绿波协调时，车辆的最小间隔时间为：

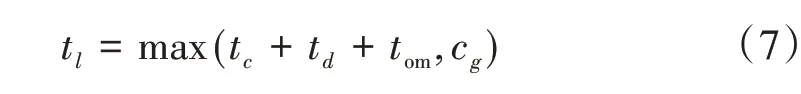
式（7）中：cg为交叉口绿波协调控制的共同信号周期时长（s）；tl,tc,td,tom意义同前。

在这种情况下，车辆的发车间隔时间应与绿波协调的信号周期相同，在一个信号周期内只允许一辆有轨电车通过。有轨电车线路信号优先的协调控制，与交叉口间距、绿信比等多因素相关[17-18]，不再赘述。计算不同信号周期下有轨电车的线路通行能力，结果如图5所示。

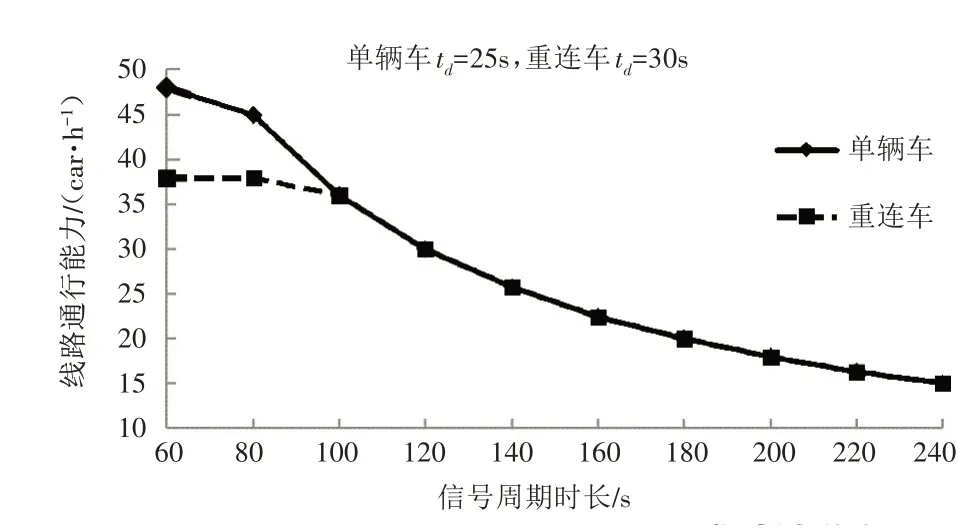
图5 不同信号周期下的线路通行能力

从图5 可以看出，当信号周期时长为75～95s时，有轨电车单辆车的线路通行能力大于重连车的线路通行能力；当信号周期时长大于95s 后，单辆车和重连车的线路通行能力相同，均完全受制于信号周期时长；当信号周期时长过大时，线路通行能力过低。因此，当交叉口信号周期过长时，可将车站设置在路中，以降低交叉口信号控制对最小发车间隔的影响。不过，路中设站可能影响有轨电车的运营速度，故也可采用立交以分离平面交叉口，提升线路通行能力。

2.3 车辆的载客容量

车辆载客容量由车辆定员和高峰小时利用率来综合决定，可按下式计算：

式（8）中：B意义同前；B0为有轨电车的车辆定员（p/car）；δ为高峰小时利用系数。

车辆定员与车辆空间、站立标准、座位数等有关。国内有轨电车的站立标准[19]取6 人/m2，2.65m宽的单辆车车辆定员约为300人，重连车车辆约为600人。

高峰小时利用率是指在实际运营中，有轨电车车内能够实际利用定员的比例。受车厢内站立的不均匀性及车内人员流动性等的影响，车辆越长，高峰小时利用率越小，单辆车的高峰小时利用率常取0.9，重连车的高峰小时利用率常取0.85。

2.4 典型情况下有轨电车客运通行能力

将以上的相关参数代入式（1）后，可计算得到各典型情况下的有轨电车客运通行能力。

2.4.1 无信号协调控制下的客运通行能力

取有轨电车线路通行交叉口所在相位的绿信比为0.3，分别计算单辆车和重连车在不同交叉口信号周期时长下的客运通行能力，结果如图6所示。

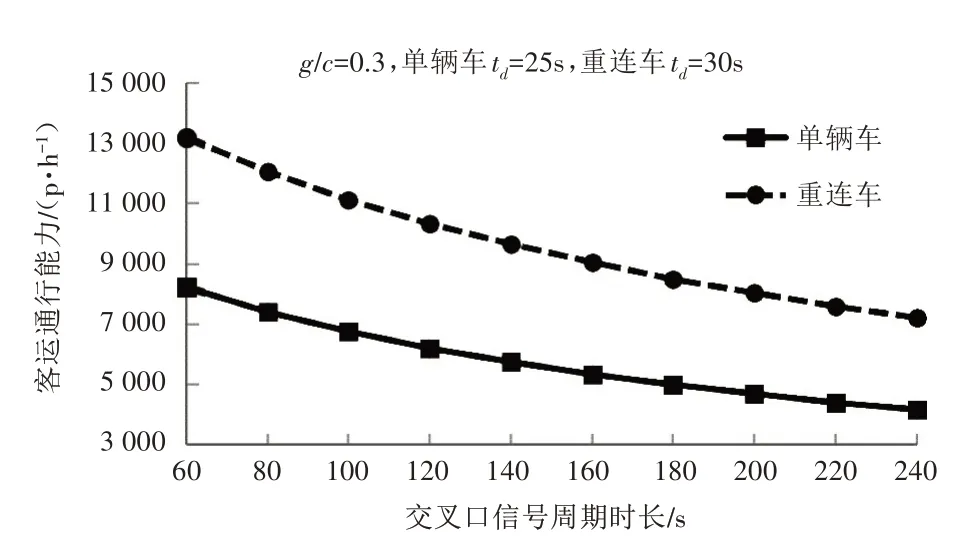
图6 无信号协调控制时有轨电车客运通行能力

从图6 可知，在无信号协调控制下，信号周期时长为120s 时，单辆车的客运通行能力为6 000人/h左右；重连车的客运通行能力为10 000人/h左右。

2.4.2 信号协调控制下的客运通行能力

当实现信号协调控制时，有轨电车可按照不同周期有序通过。计算单辆车和重连车的客运通行能力，结果如图7所示。

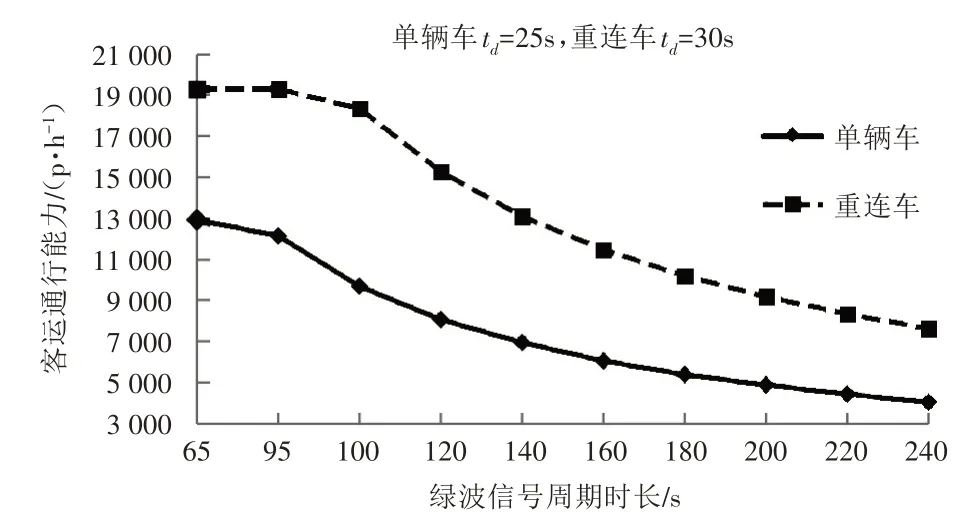
图7 信号协调控制时有轨电车客运通行能力

从图7 可知，在信号协调控制下，信号周期时长为120s时，单辆车的客运通行能力为8 000人/h左右，重连车的客运通行能力接近15 000 人/h，故通过信号协调控制能大幅提高有轨电车的客运通行能力。

2.4.3 信号协调控制的效益

不同信号周期时长下，计算有信号协调控制下的有轨电车客运能力相对于无信号协调控制时的客运通行能力的提升率，如图8所示。

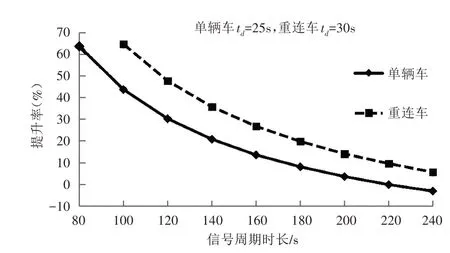
图8 信号协调控制对客运通行能力的提升率

从图8 可以看出，信号周期越短，绿波协调控制对客运能力的提升效益越大，且重连车相对单辆车的效益更为明显，究其原因是信号周期时长较短时，车辆发车间隔较短，与信号之间难以协调控制，需要的运营裕量所占比例越大，对客运能力的影响越大。一般情况下，交叉口信号周期时长为120～180s，有轨电车客运通行能力的提升效率可达20%～40%。

3 结语

有轨电车采用编组车辆、单站位的运行方式，一个信号周期只能通过一辆有轨电车，需要控制较低的进站失败率，其客运通行能力直接受交叉口信号控制的约束。本文以站点处的通行能力为基础，研究了信号无协调控制和协调控制下的线路通行能力和客运通行能力。从研究结果来看，信号协调下单辆车客运能力可达8 000 人/h，重连车接近15 000 人/h，与工程设计的客运能力总体一致。本文从理论层面阐述了客运能力实现与信号控制之间的关系，即交叉口信号周期越长，客运通行能力越低，故应控制好交叉口规模以降低信号周期时长；信号协调控制能明显提升客运通行能力，应作为有轨电车系统建设的重要组成部分。

当然，实际工程中，有轨电车的客运通行能力受交叉口组织、站点位置、站台空间、售票方式等多种因素的影响，停站时间及安全间隔距离等要根据实际工程进行测算。因此，本文公式在实际应用时需结合具体情况进行修正以得出与实际相符的客运通行能力。此外，在网络运营时，如何提升共线段的客运能力是下一步需要研究的方向。