悬挂式单轨双线曲线轨道梁的设计研究

赵晓梅,吴 琰,马 骉

(上海市政工程设计研究总院(集团)有限公司,上海 200092)

引言

悬挂式单轨交通起源于德国，先后在德国和日本得到应用，建成多条运营线路[1-2]，具有安全性高、空间利用率高、占地少、线路适应性强、工程周期短等优点，能够很好地满足中小运量城市旅游和通勤交通的需要，具有广阔的发展前景[3-5]。中唐空铁科技有限公司于2016年在成都建成我国首条悬挂式单轨试验线[6]，线路长1 410 m，通过新能源锂电池给系统供电。北京中建空列集团有限公司于2018年在开封建成一条试验线，线路长度约830 m，采用接触轨方式供电。

悬挂式单轨交通的车辆悬挂在轨道梁底部运行，因此轨道梁为底部中间开口的箱形截面，走行轮、导向轮以及供电系统设备均在轨道梁内。其中，车辆走行轮作用在轨道梁底板上、导向轮作用在轨道梁左右腹板内侧。轨道梁既是车辆荷载及线路设施的承重结构，又兼作车辆的走行和导向轨道，即“梁-轨”合一的构件。

轨道梁通过销轴或支座支承在桥墩上。双线下部结构采用独柱墩，轨道梁布置在柱头两侧的挑臂上，如图1所示。

图1 轨道梁效果图

随着国内悬挂式单轨交通试验线建设及工程推广应用，在轨道梁桥的设计施工等方面取得较大的研究进展。例如，对30 m跨径的大断面形式轨道梁和桥墩分别进行的研究分析[7]；对30 m跨径的小断面形式轨道梁-墩进行的整体分析[8]；分析加劲肋对悬挂式单轨轨道梁挠度的影响[9]。肖云霞等以用钢量最小为目标函数，考虑轨道梁跨距和梁板厚度变化，对轨道梁进行了结构优化设计[10]。庞林等研究了地震作用下悬挂式单轨结构动力特性[11]。还有报道对列车与轨道梁桥系统动力性能进行理论与试验研究[12-14]，以及对轨道梁的制造工艺进行研究[15-16]。上述文献主要针对直线轨道梁进行分析研究，对曲线轨道梁的探讨鲜有涉及。

潘西湘对直线轨道梁和半径100 m的曲线梁进行了优化设计研究[17]，研究对象为独立的单根轨道梁结构。韩冰等研究了悬挂式单轨最小曲线半径及缓和曲线的计算方法与取值，当满足舒适度要求时，运行速度20～65 km/h对应的曲线梁半径最小为30～250 m[18]。实际工程设计中，综合考虑线形和运行速度，最小曲线半径一般取50 m。

为满足导向面和走行面的制作精度要求，轨道梁一般采用钢结构。由于轨道梁为底部开口的薄壁结构，抗扭刚度较小。一般直线段简支梁经济适用的跨径为20～30 m。位于曲线段时，弯扭耦合作用导致轨道梁变形较同跨径直线梁大幅增加，适用跨径减小。目前国内已建悬挂式单轨交通线路，小半径曲线段均采用小跨径布置，在成都中唐试验线中，曲线梁跨径根据半径情况取12～20 m[6]。

曲线段轨道梁适用跨径过小，对于工程建设非常不利。当线路沿市政道路布置时，线路转弯曲线段一般位于地面道路交叉口位置，小跨径曲线梁布置将增加桥墩数量，且需要辅助采用门式墩跨越地面道路，使得行车视线的通透性差，且景观性差。此外，道路交叉口过多的桥墩数量，将限制地下管线的布置或增加管线搬迁量，增加建设难度。

根据悬挂式单轨曲线轨道梁的受力特点，研究用于双线轨道梁的横梁及其连接构造，以增大曲线轨道梁的适用跨径，提高列车运行的安全性和乘坐舒适性。

1 技术标准

本文仅列出悬挂式单轨车辆荷载及结构变形相关技术标准，其余按TB 10002—2017《铁路桥涵设计规范》的规定取值。

目前悬挂式单轨交通暂无国家和行业统一标准，相关技术标准根据四川省地方标准DBJ51/T099—2018《悬挂式单轨交通设计标准》[19]和河南省地方标准DBJ41/T217—2019《悬挂式单轨交通技术标准》[20]取值。

1.1 车辆荷载

(1)列车竖向静活载：每节车4个轴，单轴重50 kN，轴距如图2所示。

图2 列车竖向静活载图示(单位：mm)

(2)列车动力系数(1+μ)

1+μ=1+20/(45+L)

式中，L为桥梁跨度，m。

(3)动态侧向力(列车横向摇摆力)：取列车设计荷载单轴重的25%。在轨道梁车辆走行面位置，以水平集中力的形式作用于垂直轨道梁轴线方向。

(4)列车制动力或牵引力：取竖向静活载的15%，沿线路纵向作用于轨道梁的走行面处。

1.2 结构变形要求

轨道梁结构变形需要满足如下要求。

(1)在列车静活载作用下，简支轨道梁的竖向挠度不应超过其跨度的1/1 000。

(2)在列车静活载作用下，由于挠度产生的梁端(单端)竖向折角不应大于3‰rad。

(3)在列车荷载、横向摇摆力、离心力、风力和温度力的作用下，桥墩横向水平位移差引起的轨道梁端两侧水平折角不得大于4‰rad。

2 曲线轨道梁受力分析

曲线梁主要的受力特点是当梁截面发生竖向弯曲时，因曲率影响，将产生扭转，而这种扭转作用又将增大梁的挠曲变形，被称之为“弯-扭耦合作用”。由于曲线轨道梁为开口薄壁截面，且截面较窄，因此抗扭刚度较小。在小半径曲线段，弯-扭耦合作用效应将更为显著。

2.1 有限元模型

简支轨道梁典型横断面见图3。

图3 简支轨道梁典型横断面(单位：mm)

一般轨道梁的有限元整体计算采用梁单元可满足计算精度要求，计算效率高。对于悬挂式单轨交通轨道梁，由于截面开口薄壁的特点，采用更为精细化的分析方法，可提高计算精度。申彦利等研究了悬挂式单轨结构有限元模型的合理性，对实体单元模型、壳单元模型、子结构方法、子模型等进行对比分析，结论是与实体单元模型的计算结果相比，壳单元模型的位移约大17.02%，最大弯矩约高10.15%，其余模型的计算结果最大误差≤8.64%[21]。考虑到壳单元模型的整体计算效率高，且从控制设计的角度是偏安全的。因此，采用壳单元进行计算。

建立3跨简支曲线梁模型，对中间跨轨道梁进行受力分析。采用Midas Civil 2019建立全桥三维有限元模型，其中轨道梁与墩柱采用板单元，承台采用梁单元模拟。承台底采用六自由度弹簧模拟基础刚度。柱头和轨道梁间采用同位移约束使得平动自由度耦合而转动自由度独立。

曲线轨道梁有限元分析模型如图4所示。

图4 曲线轨道梁有限元模型

2.2 曲线轨道梁的受力特点

直线段简支轨道梁的经济合理跨径为25～30 m。当车辆轴重为50 kN时，对于30 m跨径轨道梁，梁高取1.3 m。本节从竖向变形与梁高、跨径的关系方面，分析悬挂式单轨曲线梁的受力特点。

(1)梁高对曲线梁的变形影响

为分析曲线梁的梁高对竖向变形影响的敏感性，以跨径20 m，曲线半径60 m为例，计算不同梁高轨道梁在静活载作用下的竖向变形，结果见图5。

图5 曲线轨道梁的梁高与竖向变形关系

从图5可以看出，增加梁高可减小曲线梁的竖向变形，对于跨径20 m，曲线半径60 m的情况，采用梁高1.6 m能满足挠跨比1/1 000的变形要求，但是高跨比较大，为1/12.5，远大于一般简支桥梁的高跨比。

(2)不同曲线半径的轨道梁适用跨径

在梁高一定的情况下，计算轨道梁在不同曲线半径下的适用跨径。计算梁高取1.3 m(轨道梁内腔列车转向架和设备等要求最小梁高1.1～1.2 m)，半径R分别取∞、500，250，100，80，60 m，竖向挠跨比控制在1/1 000～1/1 100内。计算结果见表1。

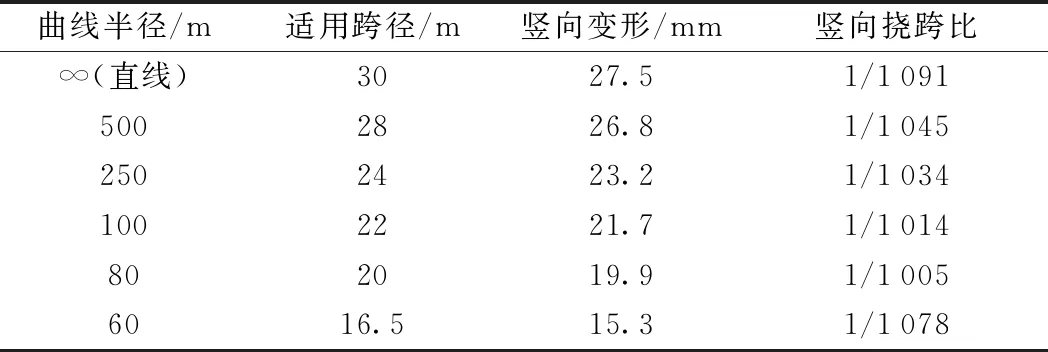
表1 不同曲线半径轨道梁的适用跨径

根据表1，由于弯扭耦合作用，使得半径越小，简支轨道梁的适用跨径越小，当半径为60 m时，适用跨径仅为16.5 m。

通过增加梁高来改善曲线梁变形会使得高跨比较大，影响景观效果和经济性。因此，为增加曲线轨道梁的适用跨径，提出一种结构设计方案，将左线、右线轨道梁通过横梁连接，以约束轨道梁的扭转，提高轨道梁整体刚度，减小轨道梁的弯扭变形。

3 横梁构造研究

横梁的构造需综合考虑结构受力、经济性、施工、景观效果等多方面因素。以提高曲线梁结构整体刚度为目标，对横梁的截面形式、间距、构造细节等进行研究。

以静活载作用下跨中截面的竖向位移、横向位移和扭转角为参数，进行分析比较。

3.1 有横梁和无横梁的对比分析

在每跨梁长范围内设3道工字形横梁，横梁高度与轨道梁一致，取为1.3 m，翼缘宽度0.8 m。横梁的顶底板与轨道梁顶底板连接，横梁的腹板与轨道梁外侧的竖向加劲肋连接。

计算比较有横梁和无横梁的曲线轨道梁在静活载作用下的竖向挠度、横向挠度与扭转变形。取左线、右线轨道梁跨中截面、内腔四个角点位置的位移进行对比分析，各点编号见图6。

图6 轨道梁跨中截面角点位置示意

有无横梁变形计算结果列于表2。

从表2数据对比，可以得到以下结论。

(1)以各项位移最大的点4和点8为分析对象，加设横梁后，点4和点8最大竖向位移分别减少70%和57%，横向位移分别减少77%和73%，扭转角分别减少77%和82%。

表2 有横梁和无横梁的静活载跨中变形

(2)横梁对轨道梁扭转变形的约束效果非常显著，提升了结构整体刚度，使得曲线轨道梁的弯扭耦合作用减小，扭转角和竖向位移大幅减小。

进一步计算表明，当梁高1.3 m、曲线半径60 m时，简支梁的适用跨径可达23 m。现将计算结果列于表3中，并与不设横梁时的适用跨径16.5 m变形进行对比。

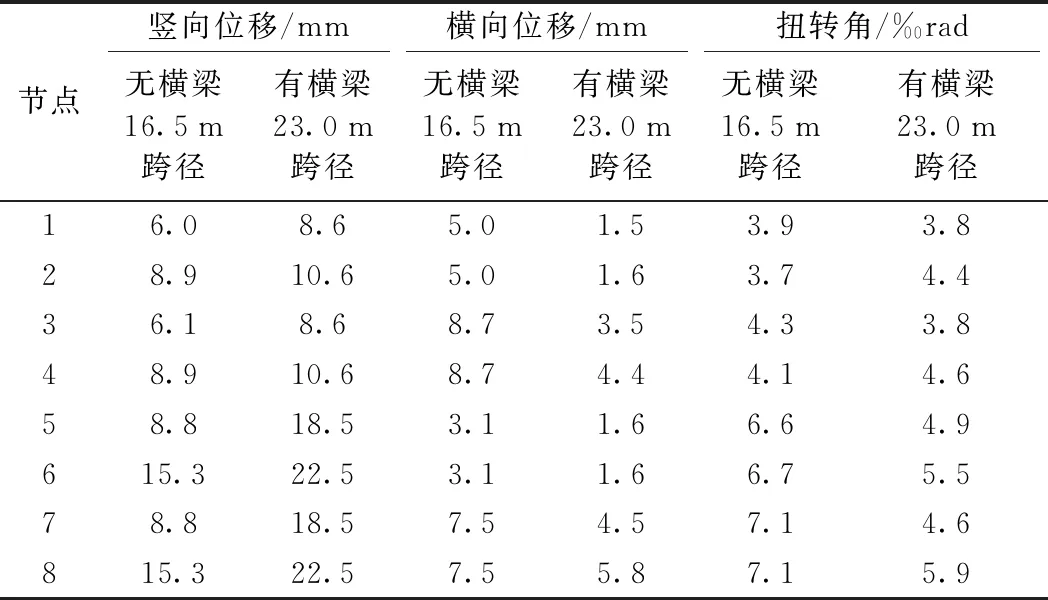
表3 有横梁和无横梁的静活载跨中变形

当曲线半径为60 m时，从表3数据对比，可以得到以下结论。

(1)对于不设横梁的16.5 m跨径轨道梁，竖向挠度为15.3 mm，挠跨比1/1 078。对于设置横梁结构的23 m跨径轨道梁，竖向挠度为22.5 mm，挠跨比1/1 022。二者均满足变形要求，设横梁后，将适用跨径增大了约40%。

(2)对于不设横梁的16.5 m跨径轨道梁，跨中扭转角为7.1‰rad，扭转率为0.43‰rad/m。对于设置横梁结构的23 m跨径轨道梁，跨中扭转角为5.9‰rad，扭转率为0.26‰rad/m。设横梁后，扭转率减小40%，可提高列车运行的安全性和乘坐舒适性。

3.2 横梁截面形式对比

横梁截面可采用工字形和箱形。为对比截面形式的影响，对跨径20 m，梁高1.3 m，半径60 m的轨道梁在列车静活载作用下的变形进行有限元分析，横梁数量均为3道。

工字形横梁腹板厚度取为24 mm，箱形横梁腹板厚度取为12 mm(工字形腹板厚度取24 mm主要为计算对比)。横梁截面分别见图7、图8。横梁模型见图9。

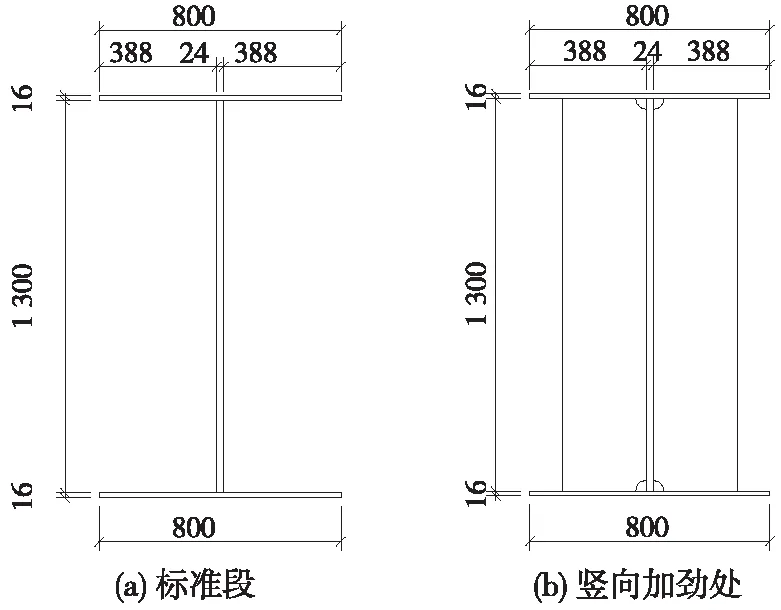
图7 工字形横梁横断面(单位：mm)

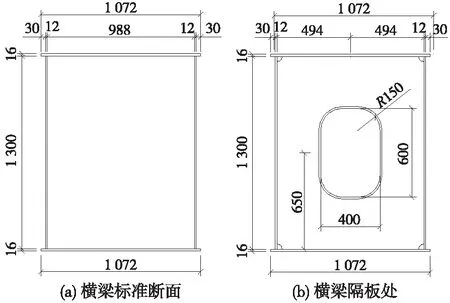
图8 箱形横梁横断面(单位：mm)

图9 不同形式横梁的模型视图

两种横断面横梁的计算结果见表4。

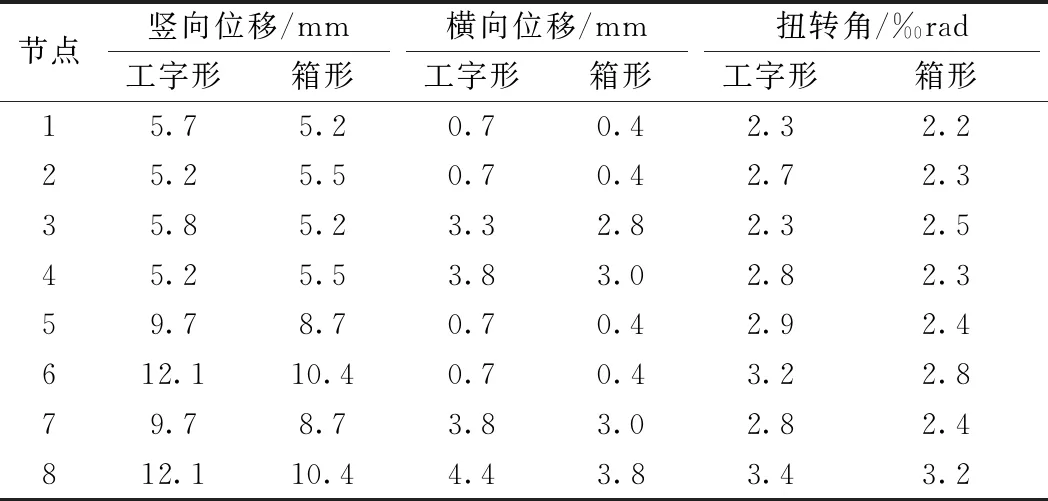
表4 不同横梁截面的静活载跨中变形

根据表4数据进行对比，可得到以下结论。

(1)横梁腹板总厚度一定时，箱形横梁自身的抗扭刚度较工字形横梁大，对轨道梁的扭转约束更强。曲线内侧轨道梁部分位置的变形略有增加，曲线外侧轨道梁各项变形值均减小。

(2)从数值来看，曲线内侧轨道梁点4竖向位移增加5%，横向位减少20%，扭转角减少16%。曲线外侧轨道梁点8的位移数值最大，为轨道梁设计的控制指标，点8竖向位移减少14%，横向位移减少15%，扭转角减少8%。

(3)与工字形截面横梁相比，箱形截面横梁使得轨道梁最大位移减小约14%，对增加轨道梁适用跨径的作用非常有效。

3.3 横梁数量对比分析

横梁数量增加，内外侧轨道梁的整体抗扭刚度进一步加强，轨道梁的扭转变形减小。但在结构刚度满足使用需求后，增加横梁数量反而带来工程量大、施工难度增大的问题，且过密的横梁影响景观，因此，应合理确定横梁数量。

对小半径曲线轨道梁采用无横梁构造时的最大适用跨径，采用工字形截面，对不同横梁数量情况下的位移对比分析。以跨中竖向位移最大点8为分析对象，将各工况对应的竖向位移结果列于表5。

表5 不同横梁数量的静活载跨中变形值

为直观分析横梁数量的影响，计算不同横梁数量相对于无横梁时的位移减小率，见表6。

表6 不同横梁数量的静活载跨中变形减小率

根据表5和表6可知，与设2道横梁相比，设3道横梁竖向位移可减小2%～3%，设4道横梁竖向位移可减小3%～5%，设5道横梁竖向位移可减小5%～7%。每增加一道横梁，竖向位移约减小2%。

进一步地，以跨径20 m，梁高1.3 m，半径60 m的曲线轨道梁为例，计算横梁数量为2～5道时，活载作用下的竖向挠度与扭转变形，见表7。

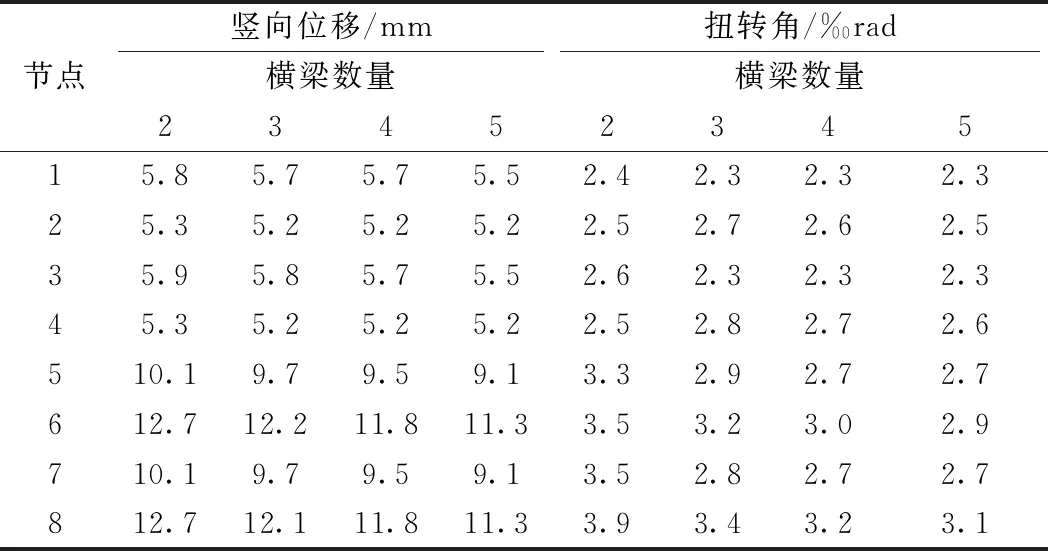
表7 横梁数量对静活载跨中变形的影响

由表7可知，横梁数量由2道增加为3～5道时，点8竖向位移分别减小5%，7%，11%，点8扭转角分别减小13%，18%，21%。

此外，对比表4和表6，对于曲线半径60 m的轨道梁，同样的横梁数量，跨径20 m比16.5 m位移减小的百分比数值更大。如5道横梁和2道横梁的位移差百分比，16.5 m跨径为5%，20 m跨径为11%。表明跨径越大，横梁作用效应更明显。

综合考虑受力、经济性、景观效果，对于跨径20 m左右轨道梁，建议设2道横梁。

3.4 横梁与轨道梁连接构造研究

增加横梁结构后，横梁与纵向轨道梁连接处是受力集中的位置，设计变高度衔接段的构造形式，有利于结构受力均匀，变形协调。

为验证衔接段的作用，对横梁与纵向轨道梁连接有、无过渡段进行计算比较。无过渡段时，轨道梁的横向加劲肋仅设在其顶板范围内。当有过渡段时，轨道梁横向加劲肋按1∶4的斜率，逐渐减小。两种布置形式的模型示意如图10所示。

图10 不同环向加劲过渡方式的模型

环向加劲有过渡段和无过渡段的曲线轨道梁在活载作用下的结构Mises应力见图11、图12。

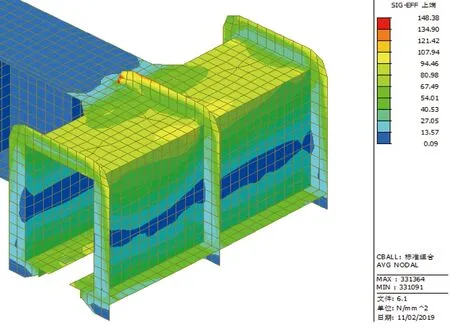
图11 环向加劲无过渡段时横梁处Mises应力(单位：MPa)

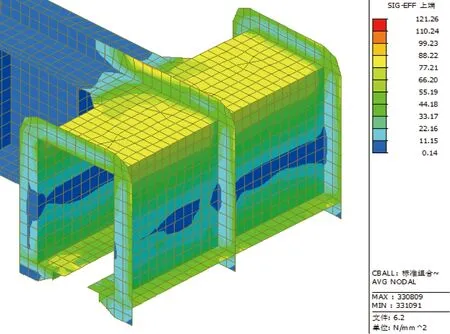
图12 环向加劲有过渡段时横梁处Mises应力(单位：MPa)

不设过渡段时，最大应力值为148 MPa。设过渡段后，最大应力值为121 MPa，减小19%，环向加劲与横梁交界处的应力集中问题得到明显改善。

4 结论

本文分析了悬挂式单轨曲线轨道梁的受力特点，提出在双线曲线轨道梁之间设置横梁以提高结构整体刚度的方案。采用壳单元建立有限元模型，对横梁的截面形式、设置间距、横梁连接构造等进行计算分析和对比。主要结论如下。

(1)增加梁高可减小曲线梁的竖向变形，对于跨径20 m，曲线半径60 m的情况，采用梁高1.6 m能满足挠跨比1/1 000的变形要求，但是高跨比较大，为1/12.5，远大于一般简支梁桥的高跨比。

(2)随着曲线半径减小，独立轨道梁的适用跨径大幅减小。当半径为500，250，100，80，60 m时，对应的适用跨径分别为28，24，22，20，16.5 m。

(3)在曲线段左右线轨道梁之间设置横梁，可有效约束横梁的扭转变形，显著提升结构整体刚度，减小轨道梁变形，增加曲线轨道梁的适用跨径。当半径为60 m时，适用跨径从16.5 m增加到23 m。

(4)采用箱形横梁截面对增加轨道梁适用跨径的作用非常有效，其跨中截面最大竖向位移值比工字形截面横梁减小约14%。

(5)横梁数量需综合考虑结构受力、经济性、景观等因素。建议跨径20 m左右轨道梁，设置2道横梁。

(6)轨道梁与横梁连接处设置过渡段可减少刚度突变造成的应力集中。使结构受力均匀，变形协调。

研究表明，曲线段左右线轨道梁之间设置横梁结构，可大幅增加轨道梁的适用跨径，解决工程建设中曲线梁跨径布置困难的问题，并可提高列车在曲线段行驶的安全性和乘坐舒适性。