高速铁路列车运行速度提高对车体加速度的影响分析

杨 飞,赵文博,孙加林,龙亦语

(中国铁道科学研究院集团有限公司基础设施检测研究所,北京 100081)

建设更高速度等级的高速铁路及提高既有线路的运行速度是当今世界铁路发展的主流趋势。随着列车运行速度的提高，列车与轨道之间的相互作用将会更加显著，线路状态对轨道系统及车辆系统的影响更加明显[1-2]。

冯青松[3]研究列车速度对轨道振动的影响，得出随着速度的提高，动态轮轨力及最大钢轨、轨枕和道床振动加速度不断增大。左玉良[4]通过对同一线路不同检测速度得到的检测数据进行对比，得出不同速度下轨道几何波形相近，仅幅值有一定的差异。赵国堂[5]指出轮轨垂向力、轮重减载率等随着列车速度的提高明显增大。罗林[6]研究车体加速度与轨道不平顺波长的关系时，简单认为普速列车车体加速度近似是轨道不平顺的二阶导数。日本根据多年运行经验推断出列车摇晃加速度正比于列车速度，但是我国和日本两国在车辆类型、线路条件、轨道不平顺特征等方面存在着差别，不能完全直接照搬照用[7]。总体而言，目前研究局限于列车运行速度对高速铁路系统动力响应影响的定性分析阶段，对于列车运行速度与车体振动影响之间的定量关系国内并未见相关研究。

近年来，既有高速铁路已大面积地恢复到设计速度运营，甚至将来有可能会提高到更高速度运行。根据高铁线路联调联试以及日常检测数据显示，目前既有高速铁路安全性冗余空间较大，提速面临的最主要问题是乘车舒适性得到保持[8]。因此有必要开展高速列车车体振动加速度与运行速度之间的关联性分析，以便掌握在相同线路工况下随着运行速度的提高，车体振动响应等指标的舒适性余量范围。

综上所述，为了准确掌握高速铁路恢复设计速度或既有线路提速等对运行舒适性的影响规律，通过对大量实车试验数据的统计及回归分析[9]，同时结合车辆动力学仿真计算结果，研究运行速度与车体振动加速度等舒适性指标之间的关联性规律，定量地给出了车体振动加速度与运营速度之间的关联性数学模型，为将来既有铁路提速提供理论支撑。

1 数据采集及处理

为了研究列车运行速度提高与车体加速度的关系，需要采集相同区段不同行车速度时车体加速度数据，因此宜选用线路开通前动态验收逐级提速期间的实测数据[10]。轨道高低不平顺主要影响车体垂向振动，轨向不平顺主要影响车体横向振动[11]，由于车体横向振动除受到轨向不平顺影响外，在曲线、缓和曲线区段还受到预设超高的影响，因此不能直接分析横向加速度与运行速度的关系，后续主要针对车体垂向振动进行分析。

本文选择设计时速350 km的8条高速铁路作为研究对象，各线路选取里程区段及对应的综合检测列车车型见表1。分别对速度等级200，250，300，350 km/h的检测数据进行统计分析。由于高速铁路平顺性较好，车体振动加速度普遍较小，因此测点多选用引起较大车体振动加速度的长波不平顺区段。此外综合检测车按照某一时速进行检测时，在线路两端有加/减速过程，分析时将剔除未达到计划检测速度级的区段。

表1 实测数据测点

选取实测数据共计413组，分析得出以上区段不同检测速度与车体振动加速度的对应关系，如图1所示。其中200 km/h检测速度所对应的车体加速度集中在(0.02～0.043)g，250 km/h检测速度所对应的车体加速度集中在(0.022～0.061)g，300 km/h检测速度所对应的车体加速度集中在(0.026～0.082)g，350 km/h检测速度所对应的车体加速度集中在(0.028～0.10)g，g为重力加速度，9.81 m/s2。

图1 不同速度检测下车体振动加速度分布

2 实测数据分析

由图1可以看出：随着运行速度的提高，车体振动加速度有整体增大趋势。为了定量地得到车体振动加速度与运行速度的关联关系，需要从车辆系统多体振动原理进行定量分析。

以余弦型轨道不平顺激励为例[12]，轨道不平顺形式为

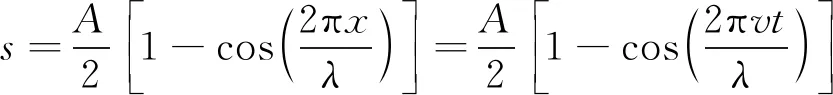
(1)

式中，s为轨道不平顺幅值，mm，同时也为轮对位移；A为轨道不平顺峰值，mm；x为到起点的距离，m；λ为不平顺波长，m；v为速度，m/s；t为时间，s。

由微积分及动力学[13]知识可知，加速度为位移的二阶导数，因此可以得出加速度计算公式为

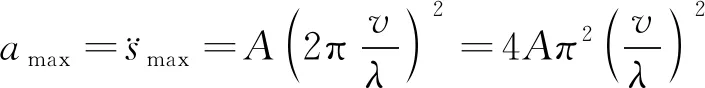
(2)

式中，amax为加速度最大值，m/s2。

可以看出，理想无阻尼自由振动条件下的车体振动加速度与列车运行速度关系如下

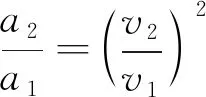
(3)

式中，v1为提速前列车运行速度；v2为提速后列车运行速度，m/s；a1为提速前列车车体振动加速度；a2为提速后列车车体振动加速度，m/s2。

式(3)表明：理想无阻尼自由振动条件下，车体加速度比与运行速度比的平方呈正比，然而实际列车运行中由于悬挂系统的阻尼耗散会衰减车体振动[14]，因此公式(3)需要根据实际的高速列车振动加速度与速度关系进行修正。

根据收集到的4个运行速度级检测数据，得到6个运行速度比及相应的车体加速度比，加速度比箱线图按照速度比大小排列如图2所示。由图2中的加速度比下四分位数、中位数、上四分位数、平均数及最值可以看出：运行速度比越大，车体加速度比也越大；同一速度比下，加速度中位数与均值近似，且除350/200 km/h运行速度比下加速度离散性偏大外，其他速度比下加速度比离散性较小，一半以上区段的加速度比集中在均值左右0.3数值范围以内，具体见表2所示。

图2 不同速度比下加速度比箱线图

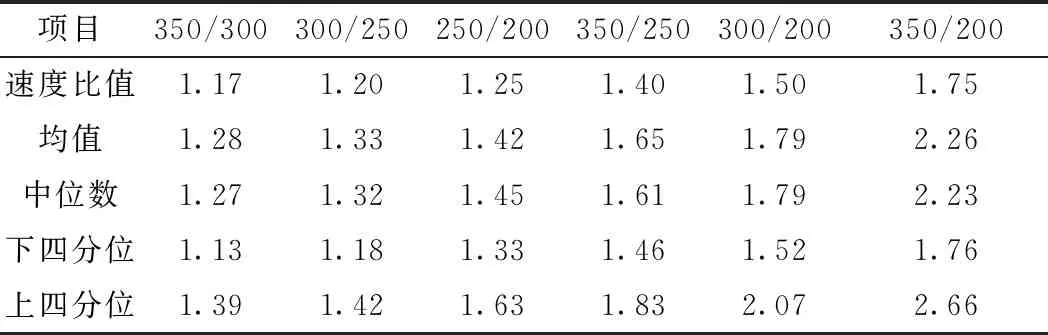
表2 不同速度比下加速度比统计结果

以加速度均值为参考，可以得出加速度比与速度比的大致对应关系，根据式(3)加速度比与速度比呈幂函数形式，因此对不同速度比下加速度比进行幂函数拟合，数值拟合结果如图3所示。拟合误差为0.02，得出拟合公式为

y=x1.46

(4)

式中，y为车体加速度比；x为运行速度比。

图3 加速度比均值与速度比关系

3 动力学仿真模型

3.1 模型介绍

采用UM多体动力学仿真软件[15]建立典型高速动车组车辆动力学模型，车辆包含车体、构架、轴箱、轮对等共15个刚体，其中除轴箱只有绕轮轴的1个转动自由度外，其余刚体均有6个自由度，分别是纵移、横移、沉浮、侧滚、点头、摇头，总计50个自由度，车辆动力学模型如图4所示，建模中所用的部分动力学参数见表3。

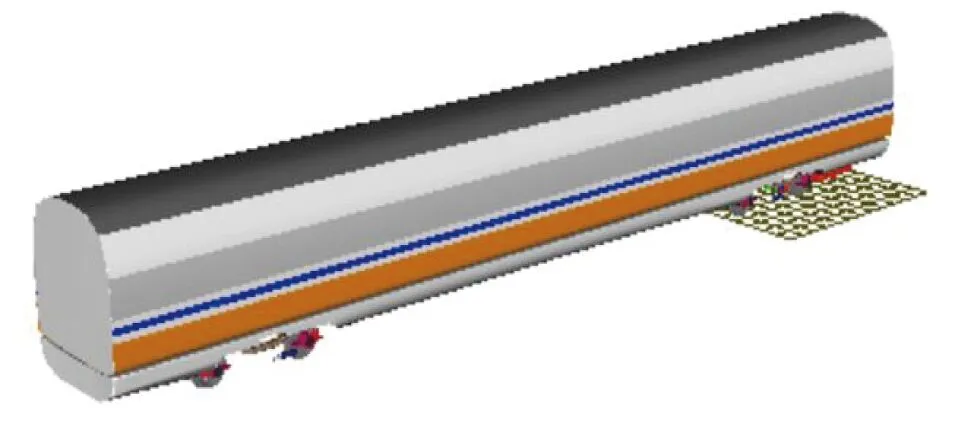
图4 高速车辆动力学模型

表3 CRH2型列车部分参数

3.2 模型验证

为了验证所建立的动力学模型有效性，结合综合检测列车[16]在现场得到的检测数据，与仿真结果进行对比分析。仿真中输入的轨道不平顺为综合检测列车实测的高低和轨向不平顺，动力学仿真模型车辆运行速度与实际检测中速度保持一致，得到仿真结果中车体垂向加速度和实车检测得到的垂向加速度，如图5所示。可以看出列车垂向加速度仿真结果与实测结果波形重复性较好。

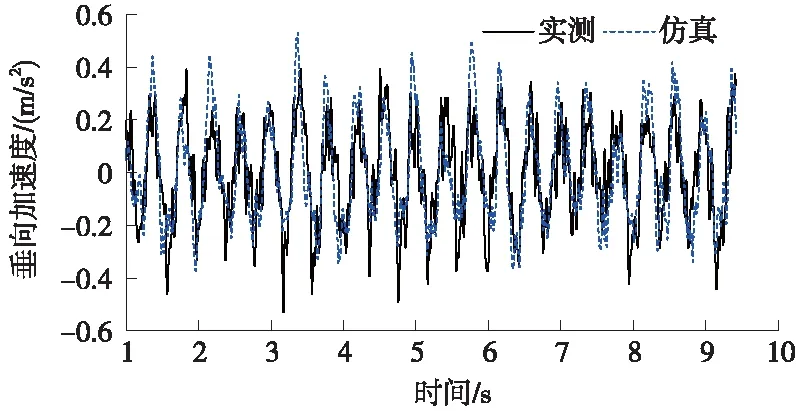
图5 仿真结果与实测结果对比

利用平均绝对误差MAE[17]、均方根误差RMSE[18]、希尔不等系数TIC与相关系数ρ[19]等指标定量评价仿真模型计算结果的可靠性，各指标计算方法如下

(5)

(6)

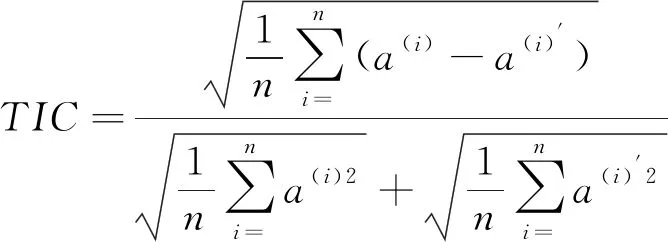
(7)

(8)

式中：a(i)和a(i)′分别为实测加速度数据a和仿真加速度数据a′的第i个值，i=1，2，…，n，n为测试数据容量；Cov(·)为协方差，Var(·)为方差。

MAE和RMSE反映了预测的绝对准确度；TIC和ρ为相对准确度指标，TIC介于0和1之间，越接近0预测准确度越高；ρ介于-1和1之间，越接近1预测准确度越高，具体结果如表4所示。结果表明：仿真计算的误差范围完全可以满足实际工程的需要，充分验证了仿真模型的准确性。

表4 准确度指标统计

4 仿真计算及结果分析

4.1 谐波轨道不平顺工况

由于轨道不平顺包含着不同的波长成分，其中中短波不平顺主要影响轮轨安全性指标，长波不平顺则主要影响车体振动加速度等舒适性指标[20]。仿真分析不同波长范围轨道不平顺作用下，列车运行速度与车体振动加速度的关联关系，轨道不平顺采用公式(1)描述的余弦波形式，如图6所示。

图6 余弦型不平顺

轨道不平顺波长选用对车体加速度影响较大的40～120 m波长，以5 m为步长，幅值选用15 mm，得到不同速度条件下的车体加速度与轨道不平顺波长关联关系，结果如图7所示。

图7 不同波长轨道不平顺激励，车体加速度与运行速度的关系

同样，统计4个速度等级数据，得出了6个速度比及加速度比的关系如图8所示。结果表明，相同速度比下加速度比离散性较小，50%以上区段的加速度比集中在均值左右0.3范围以内，具体数值见表5。

图8 不同运行速度比下车体加速度比箱线图

表5 不同运行速度比下车体加速度统计

以加速度均值为参考，得出加速度比与速度比的大致对应关系，对不同速度比下加速度比进行幂函数拟合，结果如图9所示。拟合误差为0.009，得出公式为

y=x1.54

(9)

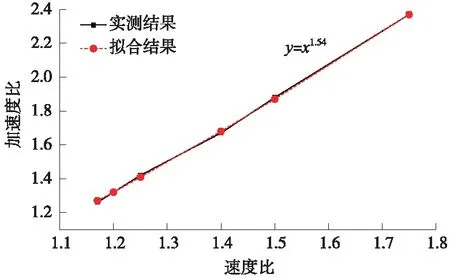
图9 车体加速度比均值与运行速度比关系

4.2 随机轨道不平顺工况

实际线路轨道不平顺为随机不平顺，然而实测数据只有一种速度等级，因此为研究随机不平顺激励下车体加速度与速度的关系，需要以实测轨道随机不平顺为输入进行仿真计算，输入的实测轨道不平顺形式如图10所示。

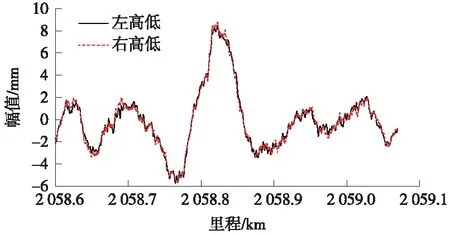
图10 实测轨道随机不平顺

列车加速度不仅与速度有关，还与轨道不平顺波长、幅值和形式等相关，因此需要选用多组数据进行统计分析。本文选取实测轨道不平顺区段100处，作为激励，分别计算不同运行速度时的车体加速度响应，得到不同速度比下加速度比如图11所示，具体数值见表6。

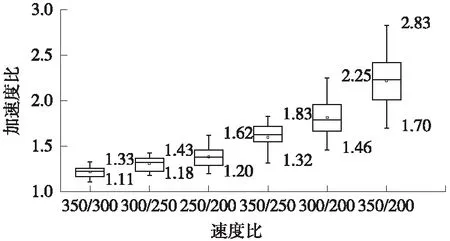
图11 不同运行速度比下车体加速度比箱线图

表6 不同运行速度比下车体加速度统计

同样以加速度均值为参考，得出车体加速度比与运行速度比的大致对应关系，对不同速度比下加速度比进行幂函数拟合，结果如图12所示。拟合误差为0.02，得出拟合公式为

y=x1.43

(10)

图12 车体加速度比均值与运行速度比关系

5 结论

通过大量实测数据统计分析及动力学仿真计算，研究既有高铁线路速度提升对乘坐舒适性的影响规律，提出车辆运营速度与车体振动加速度之间的定量关联关系。研究结论如下。

(1)结合高速铁路联调联试逐级提速实测数据，统计分析得出车体振动加速度比与运行速度比呈幂函数关系，且拟合得出加速度比与速度比的1.46次方呈正比。

(2)谐波不平顺动力仿真结果表明，加速度比与速度比的1.54次方呈正比；随机不平顺动力仿真结果表明，加速度比与速度比的1.43次方呈正比。

(3)根据综合实测数据和动力学仿真分析结果，提出车体振动加速度比与运行速度比的1.5次方近似呈正比。研究成果可以为铁路提速满足舒适性、轨道状态间接评判以及现场养护维修工作提供理论指导。