环境监测中伽马谱分块计数法探测异常放射性
2021-01-18钮云龙杨维耿
钮云龙,杨维耿
(浙江省辐射环境监测站国家环境保护辐射环境监测重点实验室,杭州,310012)
汪嘉骏
(清华大学,北京,100084)
我国辐射环境监测网,由生态环境部组织部署,各大区辐射环境监测监管机构和31个省级辐射环境监测站等单位协同建设,依托单位为生态环境部辐射环境监测技术中心(国家环境保护辐射环境监测重点实验室),至“十三五”末期,将实现辐射监测地级市的全覆盖。
美国环境保护署辐射监测网RadNet是国际上优秀的环境辐射监测系统,γ谱分块计数法是RadNet采用的一种识谱技术,将γ谱图按能量分为11个感兴趣区(图1),以每块的计数变化情况来表征对不同核素探测到与否。相较常规的峰识别法,算法简单、监测效果好[1-2]。
目前,我国在多地部署了闪烁体γ谱仪用以测量环境辐射,监测异常的辐射变化。但是,如何设置报警的触发条件,以及这些谱仪对不同放射性核素的探测灵敏度,需要进行深入研究。
本工作使用德国ENVINET公司的SARA γ谱仪系统(IGS 810型),按照美国RadNet系统的γ谱分块方式,研究此方法放射性异常是否具有检出能力,并在此基础上使用40K、133Ba、241Am、60Co 4种放射源,通过处理和数据分析,确定NaI探测器对于异常放射性的预警值,并与全国重点监测点的数据作对比,得出在实践中应当设置的预警值。
1 实验仪器和材料
实验使用德国ENVINET公司设计制造的SARA γ谱仪系统,型号为IGS 810型。探测器尺寸为3″× 3″,能量范围为30 keV~3 MeV,多道分析器共有2 048道,工作温度为-20 ℃~+60 ℃[3]。
1.1 实验准备
将探测器包装中的塑料海绵置于实验台上,探测器横置其上,完成电源、数据线路的连接。放射源样品在不使用时置于房间内离探测器较远处,以防对计数产生干扰。
1.2 实验操作
(1) 以每次测样品的前后各1 h (或1.5 h )的数据作为本底,以避免本底计数偏移造成的不良影响,样品测量1 h。即每次测量结果包含了12个有源的5 min谱图和24个(或36个)本底的5 min谱图。
(2) 由于KCl样品的活度较低,因此在测量时将2种KCl样品均紧贴探测器探头;对于另外3个点源,通过距离递增,找到计数显著升高时样品的计数最小值。每次变更距离后,记录下样品距探头的距离和此时北京时间对应的探测器时间。
1.3 数据处理
将数据导入EXCEL后,先利用谱仪提供的数据进行能量刻度,而后使用分块计数法对每个能区内的计数计算均值与方差,选择放射源γ射线能量对应的能区进行F检验,确定可行后,利用t检验判断本底与源的计数值是否有显著差异。
若源与本底的计数值差异较大,则加大放射源与探测器之间的距离,直到计数差异不再显著或在更高水平置信度下不显著为止,计算此时源的计数均值和本底计数的均值标准差之间的关系。
1.4 放射源
选取实验中使用的放射源如表1所列。

表1 选取实验中使用的放射源
2 实验结果及分析
2.1 能区的划分及检验阈值的确定
根据需要设置若干个感兴趣区,每个感兴趣区应包含一种或多种关注核素的主要特征能量峰[4]。为了便于分析,采用了表2的分区方式。

表2 能量与道址的对应关系
由于天然本底中仍然存在一定的放射性核素,因此利用SARA谱仪自带的核素检出功能中的能量与道址的对应关系,进行线性拟合:
(1)
拟合显示能量与道址之间线性关系良好。由于该探测器具有自动稳谱功能,因此可认为在实验过程中,二者关系不再变化。由式(1)得分块计数法的能区和道址的关系如表3所列。
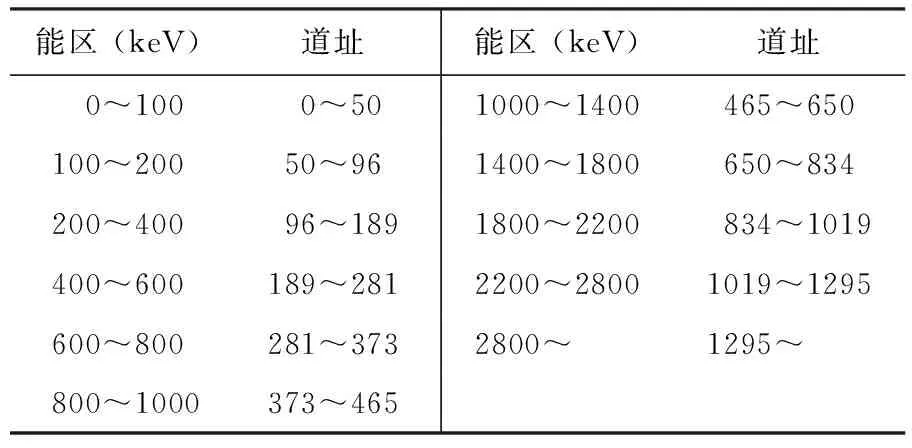
表3 能区与道址的对应关系
2.2 F检验
F检验又叫方差齐性检验,主要用于检验两组样本的方差是否相同(具有齐性)。进行F检验是比较两组样本的均值差异前必须进行的一项工作。经F检验,若认定两组样本方差具有齐性,则采用t检验法比较样本均值是否有显著性差异;若认定两组样本方差不具有齐性,则不可使用t检验法,而应使用异方差双样本检验法,如t′检验,变量变换,或秩和检验等。
F检验的检验统计量为:
(2)
取原假设为:
(3)
若取显著性水平α=0.001,则拒绝阈为:
{-∞,F0.9995(n1-1,n2-1)}∪{F0.0005(n1-1,n2-1),+∞}。
当检验统计量落在拒绝阈内时认为两样本的标准差(或方差)具有显著性差异。其中,n1,n2为两样本的样本容量。
2.3 t检验
t检验用于检验符合正态分布的两组样本间,总体平均数的差异是否显著。本实验中使用双样本t检验,检验在有源和无源时,探测器不同能区的计数值是否有显著差异,从而表征放射性同位素是否可被检出。
t检验的检验统计量为:
(4)
(5)
取原假设为:
H0:μ1≥μ2
(6)
若取显著性水平α=0.001,则拒绝阈为{-∞,-t0.001(n1+n2-2)}。当检验统计量落在拒绝阈内时认为样本1的均值小于样本2。在本研究中,取样本1为无源时的数据,样本2为有源时的数据,则某能区的检验统计量落在拒绝阈内时,代表对应能区在有源时计数有明显升高,则表征异常放射性存在,应及时做出预警。
在进行统计检验前,查表得相关的F值与t值列于表4、表5。
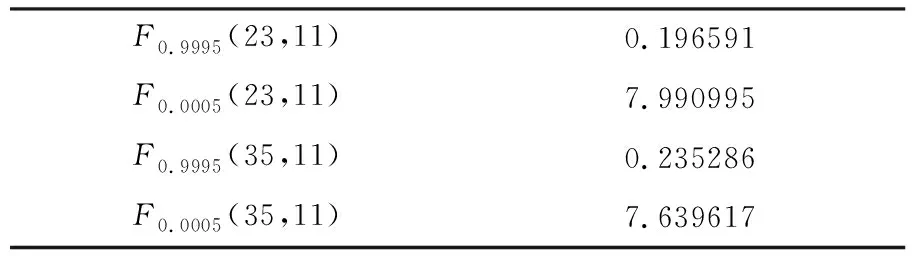
表4 F值

表5 t值
2.4 KCl大盒样品
在进行KCl大盒样品实验时,采用12组源和24组本底的数据,则对应n1=24,n2=12,由于其γ射线的能量值为1 460.822 keV,考虑到其能量展宽,因此关注1 000~1 400 keV以及1 400~1 800 keV 2个能区内的数据,结果列于表6。
在F检验之后,确定可以使用t检验,可以看出,两个能区的t值远小于-t0.00001(23,11)=-4.948995,证明在相当高的置信度下( >99.99999% ),认为源的计数均值显著高于本底的计数均值,而该样品的活度仅为6 953.86 Bq,由此可以看出,使用分块计数法时NaI探测器对于低水平的异常放射性仍然有检出功能。
2.5 KCl小盒样品
同样采用12组源和24组本底的数据,则对应n1=24,n2=12,结果列于表7。
F检验之后,确定可以使用t检验。由于:
-t0.00001(34)<-4.3624<-t0.0001(34)
(7)
-t0.0001(34)<-3.677992<-t0.001(34)
(8)
置信度为99.999%情况下,可以认为2个能区的源计数均显著大于本底计数,考虑到源的活度为441.618 Bq,进一步证明NaI探测器对于低水平的异常放射性仍有检出功能。但是,如果无法在更高水平的置信度下判断显著性差异,可认为源计数的均值接近需要预警的计数阈值。两个能区内本底均值与源的均值标准差关系为:

表6 KCl大盒样品实验结果

表7 KCl小盒样品实验结果
Y1=X1+1.42σ
(9)
Y2=X2+1.16σ
(10)
2.6 60Co点源
由于在进行此实验时发现本底数据波动较大,故增加本底数量。采用36组本底和12组源的数据,对应n1=36,n2=12。由于其γ射线的能量值为11 173、1 332 keV,因此关注1 000~1 400 keV能区内的数据。将源与探测器之间的距离递增,得到实验结果列于表8。
从实验结果可见,除第4组数据(距离122.5 cm)外,其余数据的t值均与相关的t值相去甚远,没有分析的意义。而对于第4组数据,有:
-t0.00001(46)<-4.42236<-t0.0001(46)
(11)
置信度为99.9999%情况下,可以认为该能区的源计数均显著大于本底计数。但无法在更高水平的置信度下判断显著性差异,此时有:
Y=X+1.31σ
(12)
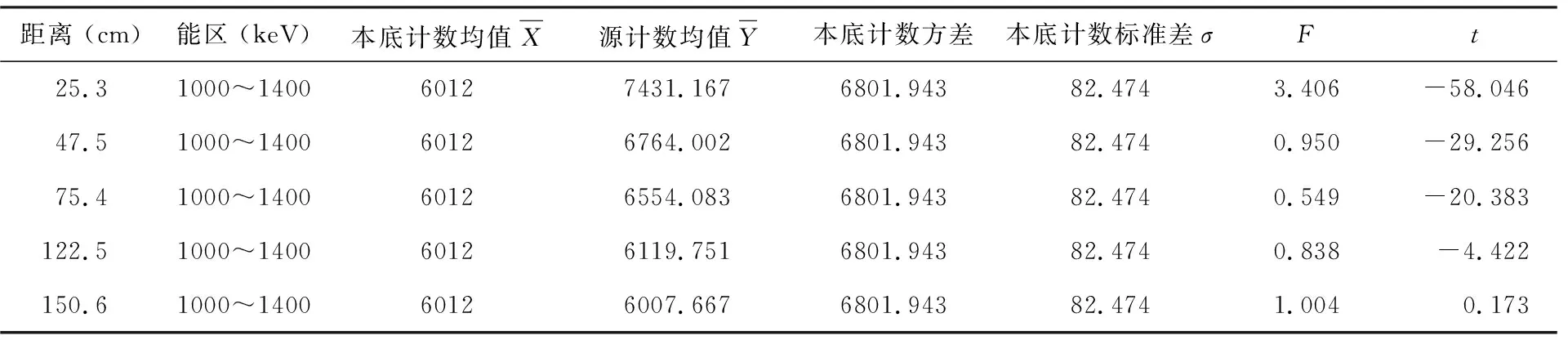
表8 60Co点源实验结果
2.7 241Am点源
采用12组源和36组本底的数据,则对应n1=36,n2=12。由于其γ射线的能量为59 keV,因此关注0~100 keV能区的数据。取距离为115.6 cm,得241Am点源实验结果列于表9。
由表8中数据有:
-t0.00001(46)<-4.3327<-t0.0001(46)
(13)
置信度为99.9999%情况下,可以认为该能区的源计数均显著大于本底计数。但无法在更高水平的置信度下判断显著性差异,此时有:
Y=X+1.32σ
(14)
2.8 133Ba点源
采用12组源和36组本底的数据,则对应n1=36,n2=12,由于其γ射线的能量为356 keV,因此关注200~400 keV能区的数据。取距离为76.5 cm,得133Ba点源实验结果列于表10。
由表9中数据有:
-t0.0001(46)<-3.6894<-t0.001(46)
(15)
置信度为99.999%情况下,可以认为该能区的源计数均显著大于本底计数。但无法在更高水平的置信度下判断显著性差异,此时有:
Y=X+1.05σ
(16)
3 结语
本研究选择了具有不同γ射线能量、不同活度的放射源,通过不同距离的摆放进行实验,使用分块计数法将γ谱图按能量分为11个区域,以每块的计数变化情况来表征对不同核素探测到与否,研究分块计数法是否能准确地探测异常放射性,同时通过对实验数据的分析计算初步得出利用分块计数法探测放射性异常时,NaI探测器应该设置的预警值。经过实验,得出以下结论:

表9 241Am点源实验结果

表10 133Ba点源实验结果
(1) 在使用KCl样本时,1 000~1 400 keV、1 400~1 800 keV 2个能区的t值在99.999%的置信度下指示测到放射性水平高于本底,而KCl样本的活度很低,这说明使用分块计数法可以监测放射性异常,且在放射源活度较低时仍能检出;
(2) 对于具有不同γ射线能量的不同放射源进行实验,得出在不同能区中源计数与本底计数的差异性介于显著与不显著之间(改变置信度可得出不同的显著性)时,源计数均值Y与本底计数均值X、标准差σ之间的关系如表11所列。
可以认为,当使用不同的置信度,各能区内计数Y显著高于或者不显著高于本底计数的条件时(即改变置信度,显著性也发生改变时),认为Y是异常放射性存在时的最低计数,而并非本底计数的统计涨落,因此可取Y=X+nσ为NaI探测器的预警值,n可取1~1.5。
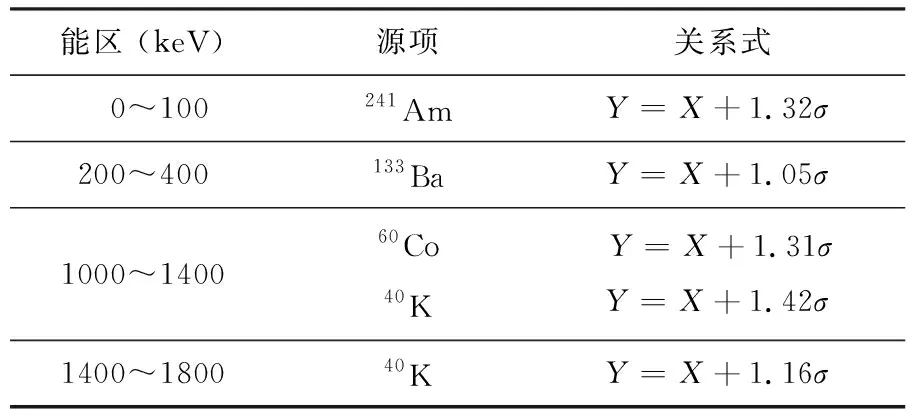
表11 源计数均值Y与本底计数均值X、标准差σ之间的关系
