基于随机方差调整梯度的非负矩阵分解

史加荣, 白姗姗

(西安建筑科技大学 理学院, 西安710055)

非负矩阵分解(non-negative matrix factorization, NMF)是寻找非负的基矩阵和系数矩阵, 即将非负数据表示为非负基下的非负线性组合, 以实现维数约简和特征提取[1]. 实际应用中很多物理特性都是非负的, 非负约束使模型具有较强的可解释性[2]. 近年来, NMF受到广泛关注, 已被成功应用到数据挖掘[3]、 计算机视觉[4-5]和模式识别[6]等领域. 乘性更新(multiplicative update, MU)[7]是求解NMF的一种有效方法, 可保证其解收敛于一个平稳点. 但MU计算复杂度较高, 故不适用于求解大规模矩阵分解问题. 随着数据规模的不断扩大, 随机梯度下降(stochastic gradient descent, SGD)算法[8]已成为机器学习, 特别是深度学习研究的热点[9-10], 其具有参数更新过程简单、 收敛速度快且计算复杂度低等特点. 因此, 将SGD算法与MU规则相结合是求解NMF的一种有效方法.

Kasai[11]将SGD算法应用到NMF的求解中, 提出了随机乘性更新(stochastic multiplicative update, SMU)和随机方差缩减乘性更新(stochastic variance reduced multiplicative update, SVRMU)规则, 分别将SGD算法和随机方差缩减梯度(stochastic variance reduction gradient, SVRG)[12]算法与乘性更新规则相结合, 对梯度估计量进行更新; 之后，Kasai[13]又提出了随机平均梯度乘性更新(stochastic average gradient multiplicative update, SAGMU)规则. 虽然这些算法取得了较好的效果, 但都未考虑偏差与方差之间的不平衡性差异, 即未对梯度估计量进行校正, 导致迭代效率较低. 文献[14]提出了一种性能优于SVRG的算法： 随机方差调整梯度(stochastic variance adjusted gradient, SVAG)算法. 该算法在迭代过程中引入参数对梯度估计量进行不断调整, 使偏差与方差达到平衡. 基于此, 本文提出一种将SVAG算法和MU规则相结合的随机乘性更新算法： 随机方差参数调整梯度乘性更新(stochastic variance parameter adjusted gradient multiplicative update, SVPAGMU)算法. 该算法结合方差缩减策略和乘性更新规则, 在梯度向量更新的同时, 引入一个参数调整梯度估计量, 不断校正梯度下降方向使其偏差与方差达到平衡, 最终快速逼近局部最优解.

1 预备知识

1.1 非负矩阵分解及乘性更新

(1)

其中‖·‖F为矩阵的Frobenius范数,W为基向量组成的矩阵,H为系数矩阵. 由于优化模型(1)是非凸的, 因此求解该模型的全局最优解非常困难, 块坐标下降算法[15]是解决该问题的一种主要方法.

针对最优化模型(1), 文献[7]提出了一种简单而有效的乘性更新规则：

H←H⊙((WTV)./(WTWH)),

(2)

W←W⊙((VHT)./(WHHT)),

(3)

其中⊙表示Hadamard积, 即对应元素之积, ./表示对应元素之商. MU规则通过交替更新W和H, 使模型(1)中目标函数在每步迭代中都减小, 最终达到平稳点.

1.2 随机梯度下降法的代表性算法

许多机器学习任务都可转化为经验风险最小化模型：

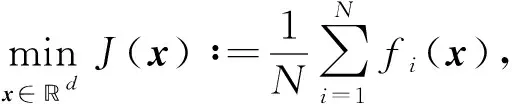
(4)

其中x∈d为模型参数,fi(x):d→是第i个样本关于参数x的损失函数. SGD算法是求解大规模学习问题的一种有效方法, 下面简单介绍几种具有代表性的随机梯度下降算法, 更多算法可参见文献[16].

SGD算法以其基本的梯度下降形式更新迭代, 在每轮更新参数时, 仅随机选取一个或几个样本计算其梯度, 并以此梯度作为全局梯度的估计值, 极大降低了计算复杂度. SGD算法的参数更新公式为

xt+1=xt-ηfi(xt),

(5)

其中参数η表示迭代步长(或学习率),i∈[N]([N]={1,2,…,N})表示第t轮迭代中随机选取的样本序号,fi(xt)表示当前迭代梯度. 由于梯度方差随迭代次数的增加而不断累加, 因此导致SGD算法收敛速度较慢.

为平衡有偏低方差的SAG算法和无偏高方差的SAGA算法, 文献[14]引入了SVAG算法, 该算法引入一个参数权值θ对梯度估计量进行校正, 即需判断随机选取的单个采样梯度fit(xt)与该样例处的最新梯度fit(xtit)之间的相关程度, 不断调整梯度使其偏差与方差达到平衡, 参数更新公式为

(6)

其中ti表示第t轮迭代中随机选取的样本序号i. 特别地,θ=1和θ=N分别对应于SAG算法和SAGA算法. 数值算例验证了SVAG算法优于SVRG算法及其他随机梯度下降算法.

2 求解NMF的随机方差调整梯度算法

设vn和hn分别表示矩阵V和H的第n列, 且n∈[N]是选取的样本序号. 最优化模型(1)等价于

(7)

图1 SVPAGMU算法的基本流程Fig.1 Basic flow chart of SVPAGMU algorithm

(8)

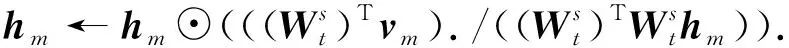
(9)

在更新W前, 为使其偏差与方差之间达到平衡, 校正梯度下降方向, 需判断随机采样梯度g1与当前快照点处梯度g2的相关程度, 记为

(10)

(11)

若‖g1-g2‖2<ε, 则选择较大的参数θ； 否则, 选择较小的参数θ. 通过θ取值的不同调整梯度估计量, 使其沿着最佳的梯度下降方向更新W. 根据SVAG算法可知： 参数θ的选取与样本数目N有关, 根据不同的数据, 判断梯度g1与g2的相关关系, 选取合适的参数θ对梯度估计量进行不断调整.

(13)

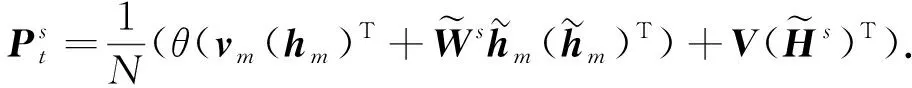
(14)

(15)

随着迭代次数的增加,αs不断缩减, 即

αs+1=ραs,

(16)

其中ρ∈(0,1). 综上可得：

算法1随机方差调整梯度乘性更新(SVPAGMU)算法.

步骤2) Fors=0,1,…, do

步骤4) Fort=1,2,…,T

步骤6) 根据式(9)更新hm；

步骤7) 根据式(10)计算g1；

步骤8) 根据式(11)计算g2；

步骤9) if ‖g1-g2‖2<ε；θ=θmax； elseθ=θmin； end

步骤14) End For

步骤15) 根据式(16)更新αs；

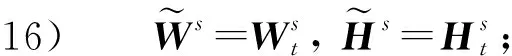
步骤17) End For.

下面讨论SVPAGMU算法在一次外部迭代过程的计算复杂度. 若内层循环最大迭代次数为T, 则更新系数矩阵H的计算复杂度为O(TMK2), 计算梯度g1和g2的复杂度均为O(TMK), 计算Q和P的复杂度均为O(TMNK), 计算S的复杂度为O(TM2K2), 最终得到更新基矩阵W的计算复杂度为O(T(M2K2+MNK)). 因此, 一次迭代总的计算复杂度为O(T(M2K2+MNK)).

3 数值实验

下面在人脸图像集和气象数据集上进行实验, 并将SVPAGMU算法与SMU,SVRMU和SAGMU三种算法进行比较. 使用MATLAB R2019a进行编程, 涉及的全部算法程序均在IntelCoreTMi7-8565U CPU @1.80 GHz 1.99 GHz处理器上运行, 操作系统为64位Windows 10系统.

3.1 实验设置

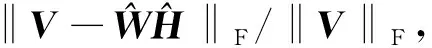
(17)

相对误差越小, 逼近性能越好.

3.2 人脸图像集

通过对人脸图像集进行测试, 比较上述4种算法的实际性能. 实验选择ORL数据集, 该数据集来自于UCI机器学习库, 是由40个不同年龄、 不同性别的人在不同时间获取的共400幅灰度图像组成, 即每个人的人脸图像10幅, 每个像素的灰度大小为0～255, 每幅图像的分辨率为64×64.

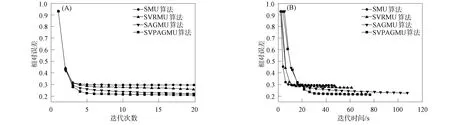
图2 不同算法对人脸图像集的迭代效率(A)和时间效率(B)对比Fig.2 Comparison of iterative efficiency (A) and time efficiency (B) of different algorithms on face image set

下面考虑K取不同值时SVPAGMU算法迭代效率和时间效率的比较. 选取K∈{20,30,40,50}, 实验结果如图3所示. 由图3(A)可见, 相对误差随迭代次数的增加而逐渐改善, 并且在同一迭代次数中K值越大, 相对误差越小; 由图3(B)可见, 随着K值的增加, 其运行时间逐渐延长. 因此, 若将SVPAGMU算法应用于较高维数据, 需选取合适的K值, 使其在迭代效率和时间效率上均达到相对最优.

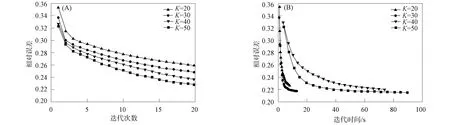
图3 不同K值下SVPAGMU算法对人脸图像集的迭代效率(A)和时间效率(B)对比Fig.3 Comparison of iterative efficiency (A) and time efficiency (B) of SVPAGMU algorithm on face image set under different K values

为更直观地说明SVPAGMU算法引入参数θ的有效性, 图4展示了目标函数的震荡轨迹, 其中横坐标表示迭代次数, 纵坐标表示当前目标函数值与最优目标函数值之差, 图中实心圆表示快照点. 由图4可见, SVPAGMU算法目标函数的震荡范围随着迭代次数的增加而不断减小, 并且震荡幅度较小, 同时快照点的变化轨迹一直保持平缓下降, 算法优化效率较高. 这是因为SVPAGMU算法在梯度更新时, 引入了调整梯度估计量的参数θ, 使其方差与偏差达到平衡, 不断地校正梯度下降方向, 沿着最优轨迹逼近局部最优解, 从而提升了算法性能.

图4 SVPAGMU算法目标函数的震荡轨迹Fig.4 Oscillation trajectory of objective function for SVPAGMU algorithm

3.3 气象数据集

选取中国661个气象台站2004—2013年共10年的相对湿度数据[19]. 为避免气象数据存在异常波动的影响, 使用每个台站10年的日平均数据. 因此, 对气象变量中的相对湿度, 每个台站的观测值由一个d=365维列向量表示, 则所有数据可表示为365×661维的非负矩阵V. 比较SMU,SVRMU,SAGMU和SVPAGMU四种算法的性能, 分别选K=15,K=30进行对比, 实验结果如图5和图6所示.

图5 不同算法在不同K值下对平均相对湿度的迭代效率对比Fig.5 Comparison of iterative efficiency of different algorithms on average relative humidity under different K values

由图5可见, 各算法的实际性能趋势与人脸图像集下的性能基本保持一致. SVPAGMU算法性能明显优于其他3种对比算法, 相对误差随迭代次数的增加而迅速减小. 当K=30时, SVPAGMU算法相对误差已达0.112 5, 说明该算法矩阵分解结果更准确.

由图6可见, SAGMU算法所耗费的时间最长, 可能是由于添加了梯度平均, 增加了计算复杂度. 随着K值的增加, 每个算法的相对误差都在减少, 但运行时间也逐渐延长. 以SVPAGMU算法为例, 当K=15和K=30时, 相对误差分别为0.137 9,0.127 5, 运行时间分别为1.63,2.47 s. 因此, 针对不同的数据需选取合适的K值, 使其在迭代效率和时间效率上都能够达到相对最优.

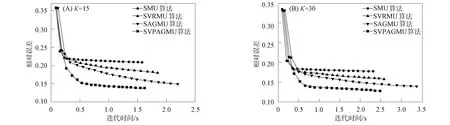
图6 不同算法在不同K值下对平均相对湿度的时间效率对比Fig.6 Comparison of time efficiency of different algorithms on average relative humidity under different K values

为检验矩阵分解的逼近性能, 先对平均相对湿度数据V应用SVPAGMU算法进行非负矩阵分解, 再将其分解得到的矩阵进行重构. 通过实验对比恢复结果与真实数据的差异, 参数设置如下： 最大迭代次数为50,K=30, 其他参数与之前设置保持一致. 部分实验结果如图7所示. 图7中随机选取的4个气象台站(台站号)分别为： 内蒙古朱日和镇(53276)、 西藏类乌齐县(56128)、 浙江丽水市(58646)和新疆巴音布鲁克(51542). 由图7可见, 重构数据与原始数据非常接近, 且重构数据振幅小, 这可能是因为NMF有效地去除了噪声. 此外, 4个气象台站的平均相对误差分别为0.084 3,0.077 2,0.089 7,0.082 3, 表明该算法逼近性能较好.

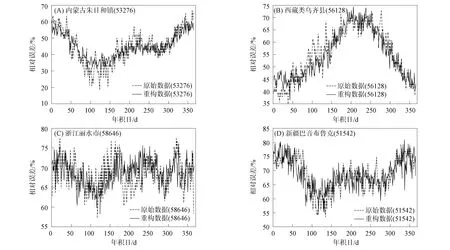
图7 部分气象台站相对湿度的原始数据与重构数据对比Fig.7 Comparison between original data and reconstructed data of relative humidity on some meteorological stations

综上所述, 针对非负矩阵分解问题, 本文提出了一种随机方差参数调整梯度乘性更新算法. 该算法将SVAG算法与MU规则相结合, 通过引入对梯度估计量进行不断调整的参数θ, 使其偏差与方差达到平衡, 从而有效提高了矩阵分解效果. 选取已有的3种算法SMU,SVRMU,SAGMU与本文SVPAGMU算法进行实验比较, 同时选取不同的K值进行分析, 结果验证了本文算法的可行性与高效性.