U 型密封结构的理论设计方法研究

赵仕志， 陈晓平， 成露， 张晓东

（东方电气集团东方汽轮机有限公司， 四川 德阳， 618000）

0 引言

提高工质压力和温度参数是提升透平机械性能的最重要手段。 随着主机参数的不断提高， 法兰连接结构的密封性问题变得日益突出。 增加密封件是改善密封效果的常用措施， 常见密封件有采用塑性变形原理的塑性密封结构和采用弹性变形原理的弹性密封结构。 塑性密封件虽然密封效果良好， 但是设计、 计算比较复杂[1]， 且不能反复使用。 相对来说， 弹性密封结构设计、 计算简单，可重复使用， 实际应用更广泛。 其中U 型或具有相似截面形状的弹性密封结构使用最广， 在新机设计和旧机改造中得到广泛应用[2]， 主要应用在汽轮机阀门阀盖密封、 管道连接件密封和垂直法兰汽缸法兰面密封等部位[3-6]， 其主要功能是防止高温、 高压蒸汽泄漏导致的经济损失和人员、 设备伤害。

对于U 型密封件， 数值方法可以非常准确快速分析密封紧力和应力水平， 国内很多学者也进行了这方面的研究[3,5-7]。 但是U 型密封结构的密封紧力和应力的影响因素比较多， 在初始设计阶段如果没有理论方法指导， 完全通过数值方法试凑，设计效率会很低。 计算机自动参数优化虽然可以解放工程师， 但是初始参数设置如果偏离最优值较远， 优化计算同样费时， 因此建立U 型密封结构快速准确的理论计算方法对提高设计效率、 减少优化时间来说是有意义的。 关于U 型密封结构密封紧力的理论计算方法比较简单， 已经有一些学者进行了相关研究[4]，但是这些理论计算方法还不够完善， 特别是对于密封结构自身应力分布的研究还鲜有报道。 本文对U 型密封结构理论设计方法研究方面的一些进展进行介绍。

1 U 型密封结构介绍

最常使用的U 型密封结构是U 型密封圈。 条形U 型密封结构因为端部的密封问题不好解决而应用较少， 但是近年来通过特殊结构设计解决了端部密封后， 条形密封结构也开始广泛应用。 无论密封圈或密封条， 其典型截面形状如图1 所示。U 型密封结构通常安装在法兰上专门加工的安装槽中， 有2 个密封面， 分别位于U 型结构的悬臂端。 密封面和安装槽间有一定过盈量。 过盈装入后过盈紧力在密封面上产生密封压力， 起到密封作用。 在工作状态下U 型结构的内侧承受高压，外侧承受低压。 压差载荷使得悬臂有张开趋势，但是受到安装约束， 不能自由变形， 所以压差载荷只能进一步增加密封面的密封紧力， 有自密封效果， 特别适用于密封高压介质。

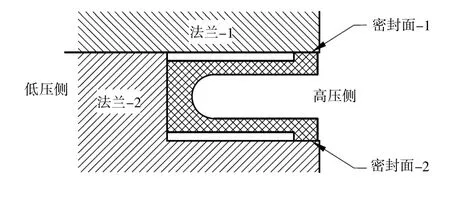
图1 U 型密封的典型结构

2 U 型密封结构的理论设计

对于U 型密封条， 可以选取单位宽度的一段作为平面问题处理。 封闭圆环状的密封环绝大多数情况下密封环径向尺寸显著小于其内径， 也可以近似等效为平面问题处理。 环形密封件的分析相对条形更复杂， 以下主要以圆环形密封圈为例进行研究。 U 型密封件在横截面内承受蒸汽力和过盈载荷。 由于U 型密封圈悬臂较长， 刚性较弱，相对来说其根部区域刚性很强。 因此可以理论地将整个根部区域近似考虑为刚体， 这样可以把悬臂部分按悬臂梁处理。 图2 是密封环的理论分析模型。 密封环悬臂长度为l， 厚度为h， 总体高度为H， 密封工作面宽度为w， 外径和内径分别为密封圈与法兰上的安装槽在径向存在装配间隙δ。 密封件高压侧压力为p， 为表述方便假设低压侧压力为0， 这样密封件的密封压差就是p。 建立以U 型截面最深处为坐标原点， 开口方向为x 轴正方向的坐标系。

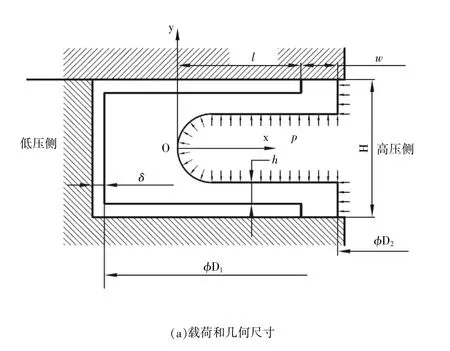
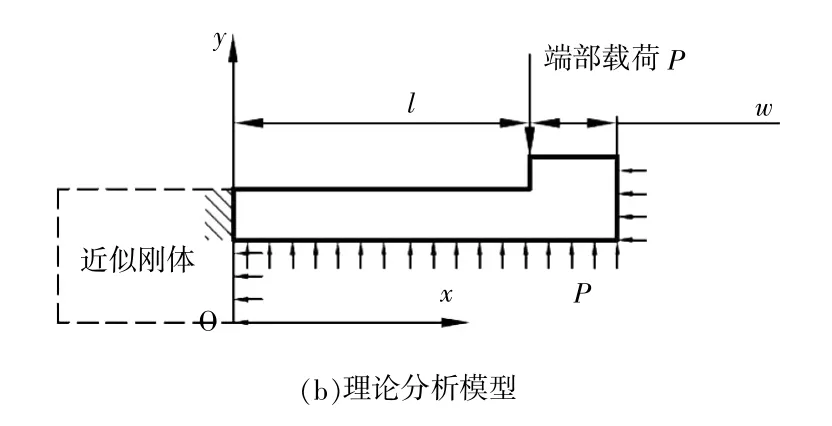
图2 U 型密封件的分析模型

2.1 密封紧力计算方法研究

如前所述， U 型密封环的过盈量由两部分组成， 一部分是密封环和安装槽间的几何过盈量注意到密封环两侧完全对称， 初始装配过盈量产生的反力由两侧悬臂平均分配。 另一部分是由于压差载荷间接产生的过盈量。 根据均布载荷悬臂梁自由端的挠度方程，的表达式为：

式中I 为截面抗弯截面模量。 因此总的过盈量为：

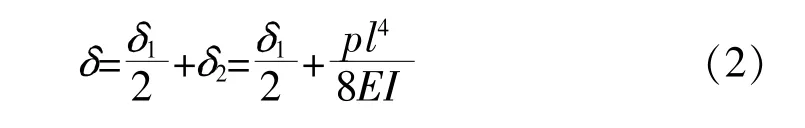
实际悬臂端部受到约束反力P， 根据变形协调和端部受集中载荷悬臂梁挠度方程， P 的计算式为：

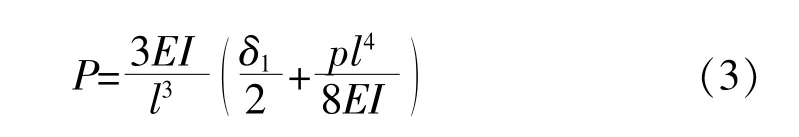
P 就是机械载荷下U 型密封件端部产生的密封紧力。 但是式（3）仅考虑了机械载荷， 实际密封紧力还必须考虑热载荷的影响。 因此还需要进一步考虑法兰部件和密封件的工作温度、 线胀系数，据此计算因热胀导致的过盈量变化δT， 并用密封件材料工作温度下的弹性模量ET代替式（3）中的E 就可以求出实际工作条件下的密封紧力PT。

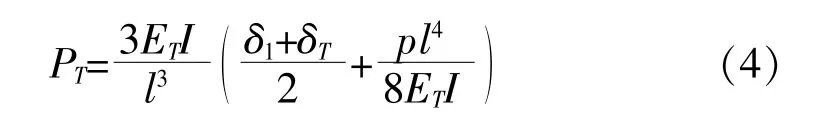
至此就完成了U 型密封件密封紧力的计算，工程设计只要根据需要的密封紧力合理设计过盈量和工作面的宽度w 就可以设计出满足密封要求的密封结构。该分析过程与唐敏锦[4]等的方法相同，但是未考虑密封件自身的应力状态， 按此设计的密封环可能不满足强度需求， 还必须分析密封环的应力状态。

2.2 U 性密封环应力分析

2.2.1 密封件横截面的面内应力分布

忽略工作面宽度w 的影响， 根据均布载荷悬臂梁弯矩方程， 沿x 方向压差载荷的弯矩方程为：

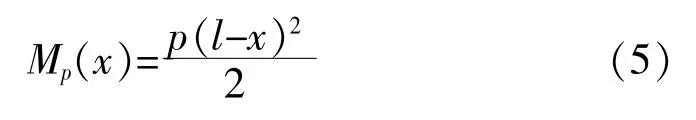
因此压差载荷导致的截面面内应力可表示为：

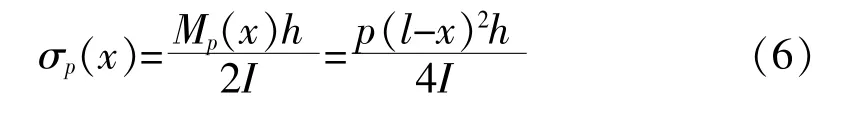
相似分析端部密封紧力PT产生的面内应力为：

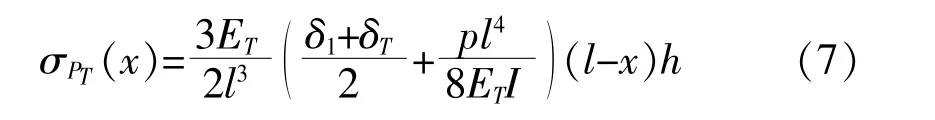
根据线性叠加原理， 两者应力场的方向相反，悬臂上总的面内应力分布可表示为：

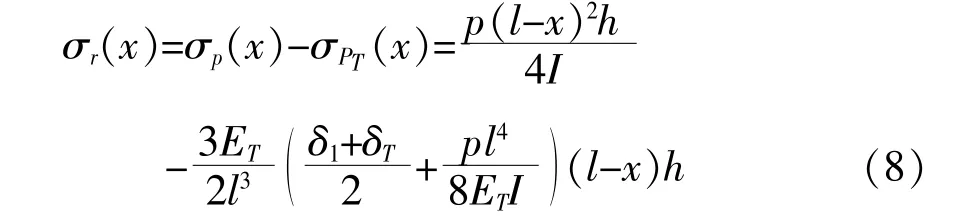
式（8）是工作状态下悬臂上面内应力分布的完整表达式， 是x 的二次函数， 根据二次函数的性质确定最值σrmax和最值位置的坐标xmax， 也就是最值在悬臂上的轴向位置。

2.2.2 密封件的面外应力分布

对于开口的密封条， 密封件横截面的法向应力近似为0， 可以忽略。 对于封闭的圆环状密封环则其横截面上存在法向力， 也就是环的切向应力。该应力根据装配的配合间隙情况有不同的表达式，具体为：

情况一： 当工作状态下密封环和法兰上的安装槽径向精确配合， 不存在装配间隙或过盈时，密封环横截面的面外应力与法兰和密封环的径向刚度相关。 根据具体的结构尺寸可以进行计算，但比较繁琐。 绝大多数情况下， 相对于法兰来说密封环的尺寸比较小， 可以近似地将密封件看作等截面薄圆环处理， 其径向刚度显著小于法兰的径向刚度。 这种情况下， 密封环会将绝大部分载荷传递给外侧法兰承担， 自身的切向应力比较小，相对于材料的承载能力来说可以忽略， 因此工程设计可以认为密封环的切向应力为0。

情况二： 当工作状态下密封环和法兰安装槽间的径向间隙够大， 密封环可以自由变形， 根据薄圆环应力方程， 其切向平均应力为：

式中A 为密封环横截面面积。

根据薄圆环位移方程， 密封环在压力作用下的径向变形为：

工作状态下密封环径向装配间隙δ0小于式（10） 的计算值时， 密封环无法完全自由变形， 结合情况一中的分析可知， 此时密封环可能的最大径向变形就是装配间隙δ0。 那么密封环的切向应力可表示为：

需要说明的是， 式（10）在过盈配合时同样成立， 只是计算应力为压应力。

结合情况一和情况二中的式（9）、 式（11）， 可以将密封环切向应力统一写为：

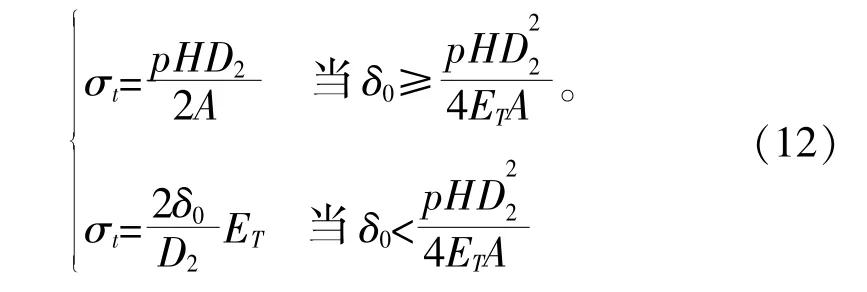
式（12）中δ0是设计工况下的间隙（过盈）， 计算时需要根据冷态装配间隙和各部件的温度、 线胀系数来计算出δ0。 从式（12）还可以看出， 实际工程设计时应尽可能使设计工况下径向装配间隙接近0 间隙状态。 此时密封环切向力为0， 这有利于减小密封圈工作条件下的应力。 而当装配间隙较大时密封环中可能存在很大的切向应力， 这对强度是不利的。

工程实际实践表明， 由于切向力计算模型简化较大， 相对于面内应力来说， 计算精度要低很多， 但是仍足以为理论设计明确方向。

3 强度评价

根据上述分析， 条形密封件近似仅受σr影响。 因此根据σr计算值和材料性质， 选择适当的强度准则就可以完成密封件的强度评价。 对于圆环形密封环， 主要受到σr和σt的影响。 同样根据材料性质选择合适的失效准则并计算相应的等效应力就可以完成密封环的强度评价。

4 计算模型的数值计算案例验证

为了验证计算模型的准确性， 用有限元算例对某垂直法兰汽缸法兰密封件做了理论模型和有限元验证计算。 验证模型的主要参数如表1 所示。图3 是验证模型的有限元计算应力场， 图4 是沿方向有限元计算应力和理论计算应力的比较。

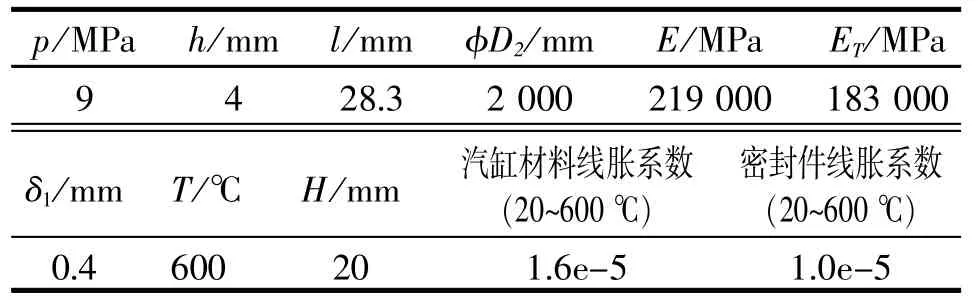
表1 有限元验证模型主要参数

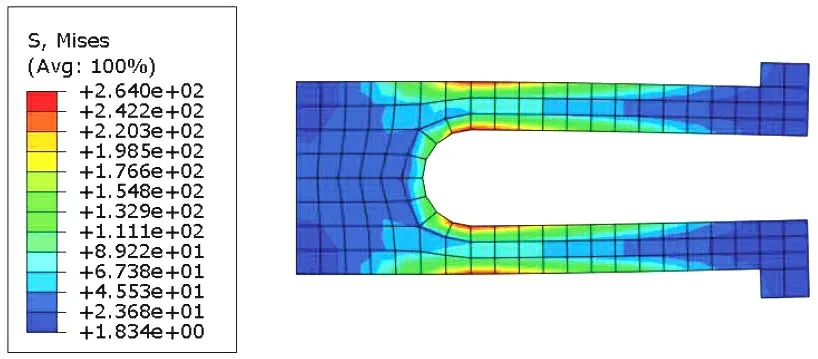
图3 U 型密封件的有限元计算应力云图（工作态）

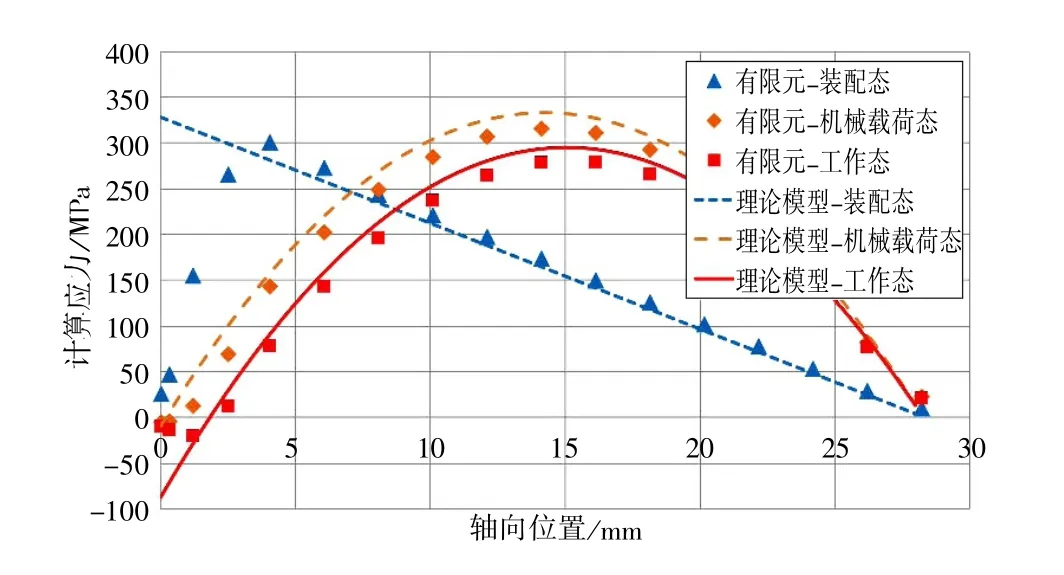
图4 有限元计算应力和理论计算应力的比较

从上述比较可以看出， 在U 型密封悬臂根部（x=0 的位置）有限元三维模型在此设置了大圆角，极大缓解了局部峰值应力， 两者的计算结果差异较大。 除该区域外， 本文各种工况下计算模型的计算结果与有限元计算结果非常接近。 两者峰值应力所在的轴向位置完全一致， 应力绝对值的偏差在10%以内。 偏差主要是因为理论计算模型在径向间隙为0 时完全忽略了密封圈的切向力。 从计算结果还可以看出， 本算例中密封件线胀系数小于汽缸线胀系数， 且部件热态弹性模量小于室温弹性模量， 工作状态密封件应力小于极限载荷工况计算应力， 理论模型准确反映了这一事实。

5 总结

本文基于简单的悬臂梁理论， 系统研究了U型密封件的设计方法。 首次用解析方法建立了包含温度、 弹性模量、 线胀系数、 装配间隙和密封压力等因素的U 型密封件全三维数学模型， 从而形成了完整的U 型密封结构设计的理论方法， 这对提高设计的效率和可靠性有显著意义。 实际U型密封结构相对于本文的案例在细节上还有各种变体， 但这些变体一般都可通过简单修正本文提出的解析模型来进行分析。

还可将材料的蠕变模型引入本解析模型， 构建出能够考虑性能退化的分析模型， 从而实现对使用寿命的可靠分析， 这将是下一步的工作方向。