指向核心素养的小学数学命题策略探析

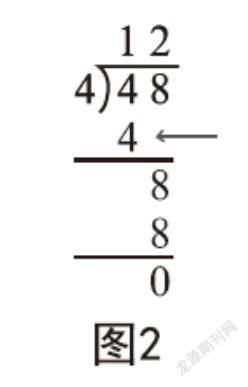
摘 要：从知识立意向素养导向转变的当下，教师应充分发挥命题的导向作用，并不断优化教学行为。文章从紧扣时代方向，渗透育人价值;革新呈现方式，培养关键能力;强化学科本位，发展数学思维三个角度，并结合案例探析小学数学命题策略，以促进培养学生核心素养目标的真正落实。

关键词：核心素养;小学数学;命题策略

中图分类号：G427                                  文献标识码：A                                       文章编号：2095-9192（2021）34-0032-02

引  言

在知识立意向素养导向转变的当下，教师要充分发挥命题的导向、评价功能，不断调整与优化教学行为，促进新课程改革的深入推进。所谓数学学科核心素养，是指具有数学基本特征的思维品质、关键能力及情感、态度、价值观的综合体现[1]。由此，小学数学命题设计应基于核心素养，从素养考查出发，关注对数学育人价值、学科本质和思维品质的考查，注重对小学生综合素质的考量，进而使核心素养的培养目标得以真正落实。

一、紧扣时代方向，渗透育人价值

长期以来，检测试题往往只停留于单纯的数学问题，缺乏生活情境、时代气息和人文情怀，这种纯粹的为解题而解题的教学方式，不仅容易让学生产生厌倦心理，还不能凸显数学学科的育人价值。由此，教师在设计命题时，应赋予试题一定的生活情境，让试题蕴含鲜活的时代气息与人文关怀，促使学生在解题的同时，接受德育教育，从而有效地落实“立德树人”这一根本任务。

例如，考查学生对“单位”这一内容的掌握情况时，由于学生对量感的建立需要结合一定的生活体验，所以笔者设计了以下试题。

案例一：在（ ）里填上合适的单位名称。

疫情无情人有情。张伯伯为了及时从上海出发为武汉同胞运送物资，他开着载重12（ ）、车身长约10（ ）的货车，开了近9（ ），大约行驶840（ ）终于到达武汉。为像张伯伯这样的最可敬的“逆行者”点赞。

这样的试题设计将真实的生活素材进行串联，将零散的知识点整合到同一生活情境中，让学生调取已有知识结构和生活经验进行对比与辨析，不但考查了学生“量感”的强弱，而且检测了学生的应用能力，同时体现了数学的育人价值。

二、革新呈现方式，培养关键能力

小学数学教师在命题时应指向学科基础知识。这里所谈的基础并非指向简单题、容易题，而是基础性题目经过形式、情境、解题策略等方面的革新，来考查学生的数学阅读能力、分析能力与表达能力等。革新基础知识命题的呈现方式，应侧重于对学生灵活运用、有机整合与评价创造能力的考查，以便教师了解学生关键能力的培养状况。

（一）从“记忆”走向“运用”

数学课堂是思维的训练场，数学试题是锻炼学生思维的材料。因此，教师在命制试题时，不仅要关注知识的形成过程，还应关注学生对数学知识的灵活运用。例如，在考查学生对平面图形知识的掌握情况时，笔者设计了下面这个题目。

案例二：将一个长方形纸张沿着其中一条直线一刀剪下，那么下面图形中（ ）是不可能得到的。

A.梯形   B.长方形   C.直角三角形   D.锐角三角形

这个试题能够引导学生根据已经掌握的“长方形的特征”进行理性判断，使他们借助数学推理得出不可能得到锐角三角形这一结论。这样的试题不仅考查了学生对长方形特征的掌握情况，还考查了学生空间观念的发展情况，同时使學生的数学推理能力得到了发展。

（二）从“模仿”走向“整合”

传统的数学命题更多的是停留于单一的知识点考查与单纯的数学技能的操练层面上，注重考查学生的模仿与记忆能力。这样的命题形式对学生的综合运用能力和创新能力的发展是不利的。因而，在命题时，教师应关注知识的融会贯通，发展学生的综合性思维和创新能力。例如，在教学完“百分数的应用”的内容后，教师往往会设计一些简单的试题。笔者侧重于知识的横向与纵向联系和融合，设计了以下试题。

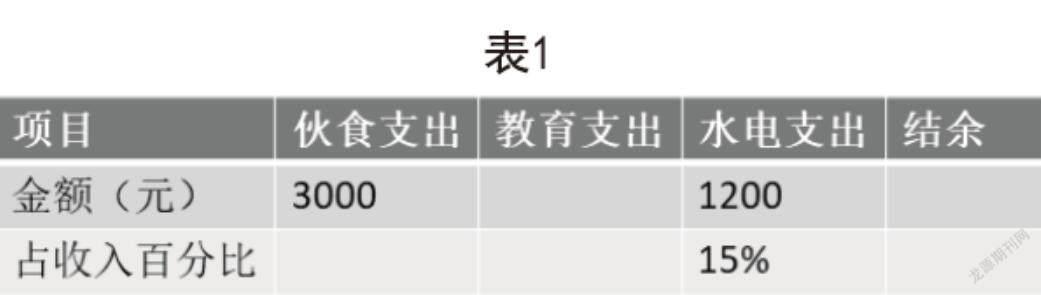
案例三：小红家八月份总收入8000元，支出与结余如表1所示。

（1）教育支出与伙食支出的比是1∶3，请将上表填完整;（2）将这个统计表制作成扇形统计图，那么教育支出部分的圆心角的度数为（ ）;（3）你还能提出什么数学问题？并列式解答。

这道题借助统计表，将比例、百分数与绘制扇形统计图等知识进行整合，让学生通过观察图表来分析数量关系，弄清各个知识点之间的联系，并整合运用各知识点，将点状的、单一的数学知识整合为网状、综合的知识体系，进而促进学生数学整合能力的提升。

（三）从“结论”走向“思想”

抽象、推理和模型是《义务教育数学课程标准（2011年版）》提出的数学基本思想，也是数学学科核心素养的重要组成部分。基于这样的认识，笔者认为，指向核心素养的小学数学命题应从传统的过于注重考查学生的学习结论中走出来，在试题设计中融入数学思想，助推学生数学学科核心素养的发展。

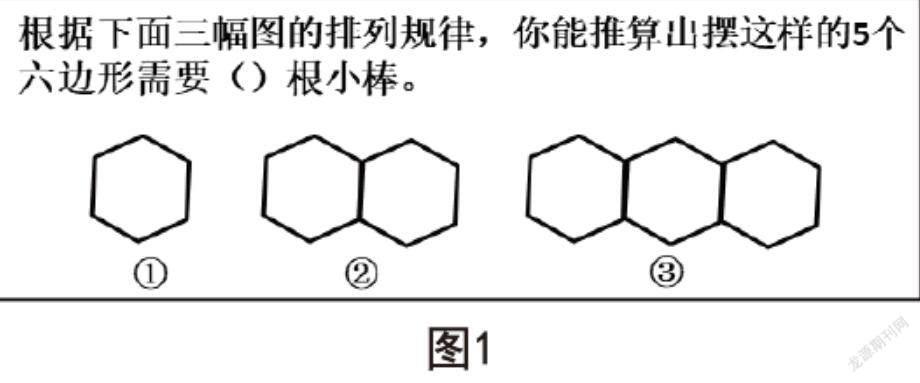
例如，图1这道试题以“以此类推”方式考查学生观察并总结已知图形排列中的简单规律，然后建立起图形小棒的总根数为“5n+1”这一数学模型，从而推理得出“要摆5个这样的六边形需要26根小棒”。这样的试题设计促使学生对前三个图形进行仔细观察与比较，通过分析、推理，提取相同的数学结构特征，建立数学模型，并运用模型解决问题，使学生不仅会算5个六边形的总根数，还能算出更多六边形这样摆需要小棒的总根数，让学生学会举一反三、触类旁通。

三、强化学科本位，发展数学思维

数学思维是数学学科核心素养的重要组成部分。因而，教师在命题时应在重视考查数学知识和技能的同时，更要注重考查学生的数学思维过程，将学生的思维深度与思维习惯作为重要的考查内容。工具性理解和关系性理解是数学理解的两个类型。工具性理解指的是只知道怎样做，属于浅层理解;关系性理解指的是不但知其然，而且知其所以然。显然，关系性理解是一种深度理解。因而，在命制试题时，教师应结合学科特点，考虑学生的数学思维是否处在深度理解这个水平上。

例如，在考查学生的运算能力时，教师通常会停留于学生是否会进行程序化演算上，只关注计算结果的正确与否，忽略了学生的思维过程，忽视了对算理的考查。针对这样的情况，笔者设计了以下试题。

案例四：有48块小面包，小明准备每4块装一盒，一共能装几盒？图2竖式计算中的箭头所指的数字4表示的是（ ）。

A.已经装了4块

B.还剩下4块

C.已经装了40块

D.已经装了8块

这样的试题设计改变了以往那种只考查学生算法的评价方式，引导学生将竖式计算过程与问题情境联系起来，理解箭头所指数字4表示的是“已经装了40块”这个现实意义。这不但有效考查了学生对“两位数除以一位数笔算除法”的算法的掌握情况，而且检测了学生对“为什么这样算”的算理的理解程度，使学生的思维过程可视化，促进了学生数学思维的发展。

结  语

综上所述，随着“素养时代”的到来，数学命题也要走出“知识时代”的旧模式，从以往注重考查“学生的学习结果”走向注重考查“学生的思维过程”，进而让命题紧扣时代方向、革新呈现方式和强化学科素养， 从而实现渗透育人价值、培养学生关键能力和发展学生数学思维的目标，使学生的数学学科核心素养得以发展。

[参考文献]

[1]胡典顺.数学素养研究综述[J].课程·教材·教法，2010（12）：50-54.

作者简介：王亚芳（1976.10-），女，福建莆田人， 本科学历，一级教师。