改进的河岸砂土冲蚀试验方法与成果分析

陈勇 董进龙 崔宪东 叶润青

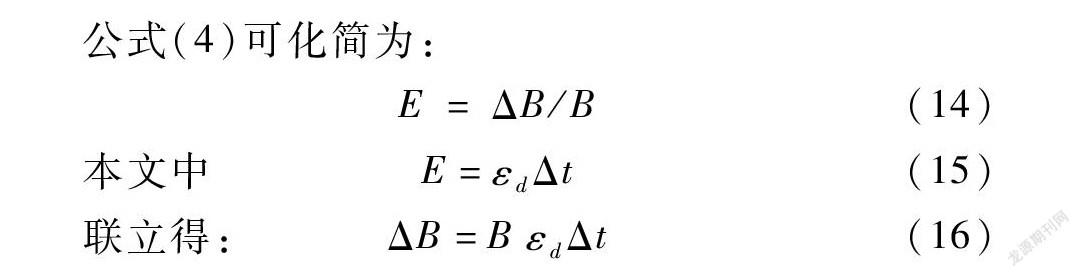
摘要：河岸砂土冲蚀对岸坡的稳定性有极大影响，对于冲蚀过程中涉及的土体起动与冲蚀速率两个方面，传统冲蚀仪器难以进行定量研究。自制了一种测试土体抵抗冲蚀能力的新型冲蚀装置，基于土体质量损失模拟河岸受水流冲蚀状态，采用河岸砂土进行试验，通过单一变量的起动试验和冲蚀试验，建立了河岸土体冲蚀数学模型。研究结果表明：① 河岸砂土冲蚀速率达到2×10-5～4×10-5 s-1时达到起动流速;② 起动流速与孔隙比成反比，与内摩擦角成正比;起动切应力可用孔隙比和内摩擦角来表示;③ 土体的冲蚀速率与孔隙比、水流流速成正相关关系;④ 同种砂土的可蚀性系数与流速的5.5次方成正比，通过冲蚀速率可直观反映河岸抗冲蚀能力。

关 键 词：起动流速; 起动切应力; 孔隙比; 水流流速; 冲蚀率

中图法分类号： TV149

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.12.030

0 引 言

研究河岸冲蚀问题有助于探究河道展宽变形规律，对岸坡防护稳定性起到建设性作用[1]。河岸砂土冲蚀问题涉及土体起动和土体冲蚀速率两个方面。国内外学者在这一领域做了大量相关研究。Briaud等[2]根据大量砂土的冲蚀试验结果，通过对土颗粒在冲蚀过程的分析得到了广义的冲蚀速率模型：

εu=Mτ-τ0ρwu2n（1）

式中：ε为冲蚀速率，m/s;u为水流平均流速，m/s;M为冲蚀系数;τ为水流切应力，Pa;τ0为土体起动切应力，Pa;ρw为水的密度，ρw=1 g/cm3。

Hanson[3]经过大量试验，提出了砂土的冲蚀速率与起动切应力的关系：

ε=Kdτ-τ01.5（2）

式中：Kd为可蚀性系数。

显然在砂土冲蚀的研究中各学者的研究重点基本一致，土体起动与可蚀性系数是影响冲蚀的关键。对于砂土起动受力，各国学者已经达成统一，起动过程中土颗粒主要受水下重力GS、上举力Fl、水流拖曳力Fw和颗粒间摩擦力FN的共同作用，但是对于起动切应力的主要影响因素各学者有不同观点。Dunn[4]认为起动切应力受塑性指数和抗剪强度影响，Yalin[5]提出流速场与起动切应力的关系，Mitchener等[6]提出了起动切应力与干密度的关系式，国内外学者提出的起动流速公式与起动切应力公式有上百种，对于砂土的起动影响因素还需进一步探究。

可蚀性系数是评价土体侵蚀难易程度的重要指标，研究初期认为某一土体的可蚀性系数是固定的，但随着研究的深入发现可蚀性系数受多种因素影响。Olson等[7]在落基山脉东部密苏里河和科罗拉多河流域内通过野外试验研究，得出土壤流失量可作为土壤可蚀性的评价指标，Chandra等[8]提出了侵蚀系数，并指出可以通过公式来量化土壤可蚀性。鲍恩俣等[9]通过对不同粒径土体的可蚀性研究，得到Kd与砂粒含量呈负相关。

针对以上两个方面国内外学者采用普通明渠水槽和封闭水槽开展了大量试验研究，试验过程中定量控制和精准监测一直是难以解决的问题。针对这一问题，笔者自主设计制造了基于土体质量损失的新型冲刷装置，一方面解决了定量研究难以控制的问题;另一方面大大提高了试验的精度，对冲蚀的损失量精确到0.1 g。通过试验研究获得土样起动切应力τ0与孔隙比e和φ的关系，可蚀性系数Kd与孔隙比和水流流速的关系及改进的河岸土体冲刷流失模型。

本文对河岸砂土的冲蚀特性展开研究，将对岸坡的防护与监测起到现实的指导意义，为河岸冲蚀研究提供了方法和思路。

1 试样制备及试验方案

1.1 试验仪器

大多数学者在进行冲蚀试验研究时，采用如图1所示的密闭环形水槽，判定土体起动和探究土体冲蚀速率的方法，主要是通过肉眼观察，存在较明显的主观误差。

土体冲蚀试验的难点是在低流速时确定冲蚀开始的时间，传统的试验仪器采用的是外部监测，从土体的外部变化来判断土体的冲蚀，这就存在一定滞后性且外部监测很难覆盖试样全部，往往是局部土体发生改变就认定土體发生冲蚀。为提高试验精度，本次试验采用的是一种自主设计制造的测试土体抵抗冲蚀能力的新型冲蚀装置（见图2），从外部监测转向内部监测，从局部观察转向整体观察。该装置的试样盒伸入水流稳定段内，电子天平连接质量采集系统，对试样盒中的土体质量进行实时的记录（见图3）。水流稳定段内设置有流速测量仪，精确测定水流流速。该装置的优势主要有以下几点：① 通过试样自身质量变化进行监测，质量采集系统可精确得知随时间变化被水流冲蚀带走的土颗粒质量，确定试样冲蚀开始时间，减小主观误差。② 将试样化作一个整体，避免了局部观测的误差。制样方便，易控制试样的物理指标。③ 新型冲刷仪器多档位调节水流流速，进出水比例控制试样水深，计算机数据采集更准确高效。

1.2 试验土样及制备

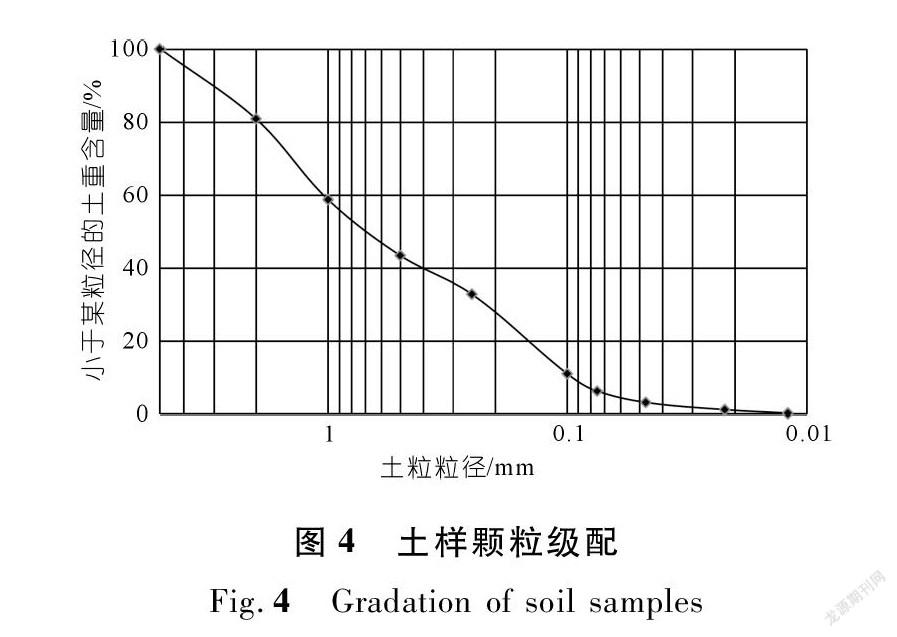
试验原状土样采自宜昌市某河岸岸坡土体，通过颗分试验和密度计法测定其颗粒级配，土样为颗粒级配不良的砂性土，如图4所示。

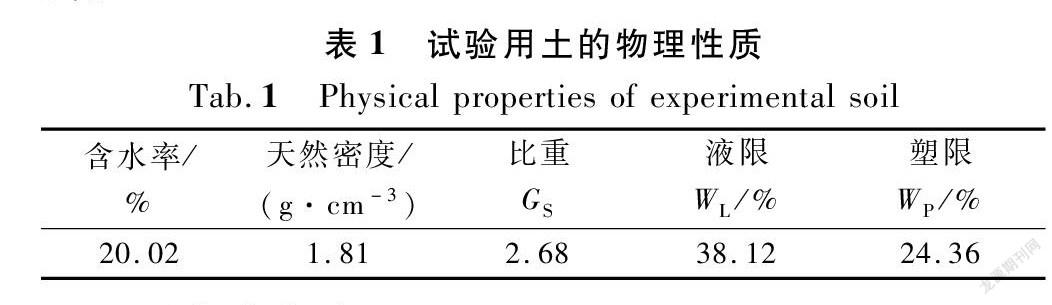
其塑限指数IP=13.76，液限指数<0，其他的物理性质见表1。

本次试验土样采用重塑土，土样采用锤击方法碾压，一方面使土样的各个部分均匀、密实;另一方面可以较好地控制土样的高度和孔隙比。因本试验研究的是饱和土体的抗冲蚀特性，土样抽真空后饱和24 h取出。

1.3 试验方案

为探究河岸冲蚀公式，本文基于同种粒径和水深条件，对河岸无黏性砂的临界起动流速与孔隙比和内摩擦角关系、冲蚀速率与孔隙比和水流流速的关系进行分析。分别进行了9组单一变量的对比试验，如表2所列。

2 试验结果

基于河岸饱和土体的抗冲蚀特性研究，本文引入了比值定义的冲蚀比：

E=MSM0（3）

式中：E为冲蚀比;MS为冲蚀流失的土颗粒质量，g;M0为土样土颗粒总质量，g。

2.1 起动流速测定

研究饱和土体的抗冲蚀能力，首先要测定土样的起动流速。目前有多种方法测定土体的起动流速：① 观察法[10]（饱和土体抗冲刷的起动过程分为弱动、中动、强动，一般以弱动或中动为起动标准）;② 冲刷速率定量法[11]（标准Shelby管中圆柱土体在冲蚀过程中高度下降的速率0.4×10-3～0.8×10-3 cm/s作为起动标准）;③ 浊度计法[12]（利用浊度计测试）。这3种方法受人主观性影响比较大，起动流速的测量存在一定的误差。为尽可能减小起动流速判别的主观性，本文采用观察法与质量采集系统测定土体质量损失率相结合的方法。

采用变频水泵和上水管道阀门来控制流速，在观察土颗粒流失的过程中注意数据采集系统的试样质量变化率。经过多次测量并结合其他学者对砂土体起动的判别标准，最终得到基于土体颗粒质量损失的起动判别标准。土体的冲蚀速率εd：

εd=E/t（4）

式中：εd为冲蚀速率;E为冲蚀比;t为冲蚀时间。

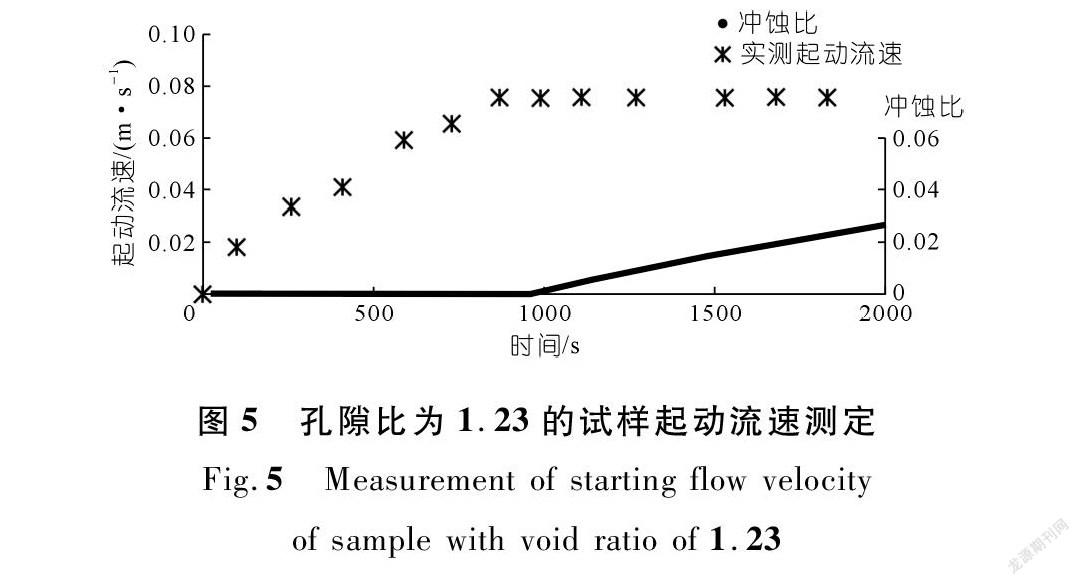
图5为孔隙比为1.23的试样其起动流速测试曲线。冲蚀开始时设定一个较低的水流流速，观察到试样盒中土样没有土颗粒流失，与此同时质量采集系统显示试样质量没有损失;缓慢增加流速直到观察到土样开始流失，保持此流速不变，分析质量采集系统的数值变化;当水流流速达到土体临界起动流速时，试样质量开始损失，保持流速不变，试样质量匀速损失，可以判断此流速为土体的起动流速。根据测算，冲蚀速率达到2×10-5～4×10-5 s-1时砂土试样达到起动流速。

2.2 起动流速与孔隙比、内摩擦角的关系

土体的起动，先是松动过程，再是起动过程。孔隙比表示土体的结构性，土体的结构性对土体松动过程有很大影响。内摩擦角反映土的摩擦特性，本文以滚动起动作为无黏性砂起动过程，土颗粒滚动过程中所克服的摩擦力与内摩擦角φ有密切联系。当前土体起动的研究中将孔隙比和内摩擦角相结合的研究还是很少见的。

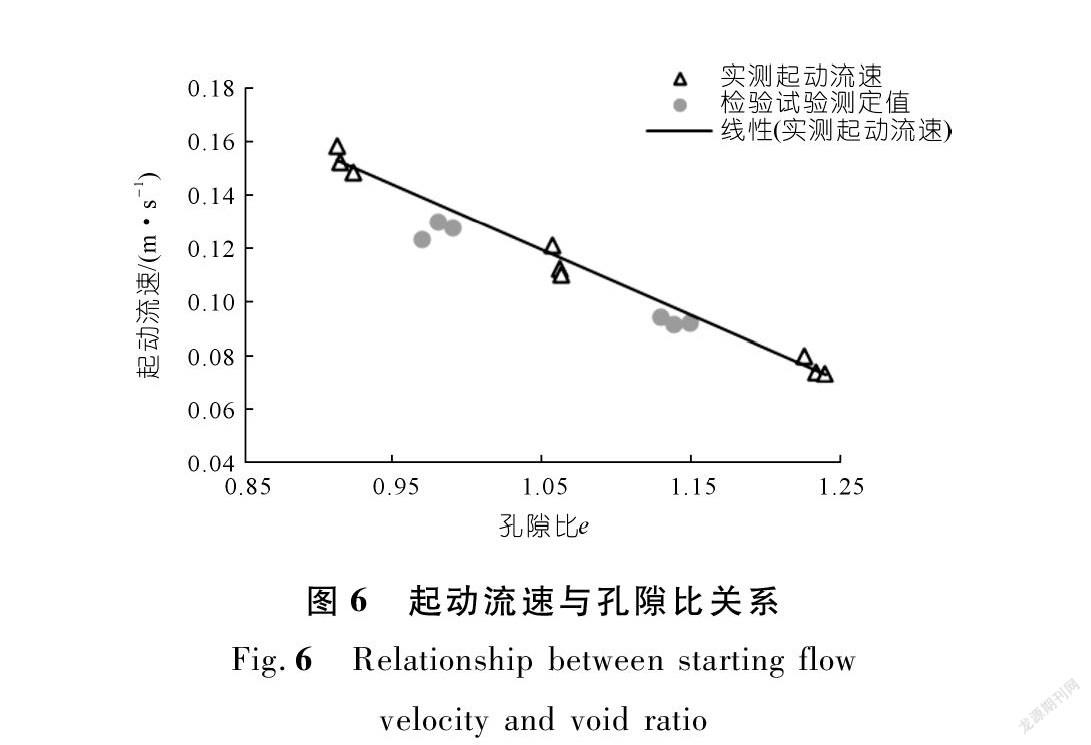
试样的孔隙比越小，试样越密实，所需的起动流速就越大。如图6所示随孔隙比的增加，土体的起动流速在降低，符合土体越密实越难以起动的现实。公式为

v0=-0.24e+0.375（5）

结合内摩擦角φ对砂土起动的影响。取试验土样测定孔隙比为1.23，1.06和0.92时的内摩擦角φ。公式为

v0=0.0541φ-1.55（6）

本文基于同种粒径和水深条件，综合考虑土体起动过程中的两个阶段：即孔隙比e和内摩擦角φ对土体起动的影响，利用Origin软件拟合得到v0与孔隙比e、内摩擦角φ的关系，结果如表3所列。

v0=-0.14e+0.023φ-0.445（7）

5组试验中，试样孔隙比与内摩擦角变化较小，且二者相互影响。实测起动流速与计算起动流速的最大差值仅为0.008 m/s，说明式（7）计算所得起动流速较为合理。

经过5组试验，实测起动流速与计算起动流速的差值在3%～7%之间，说明式（7）计算所得起动流速较为合理。

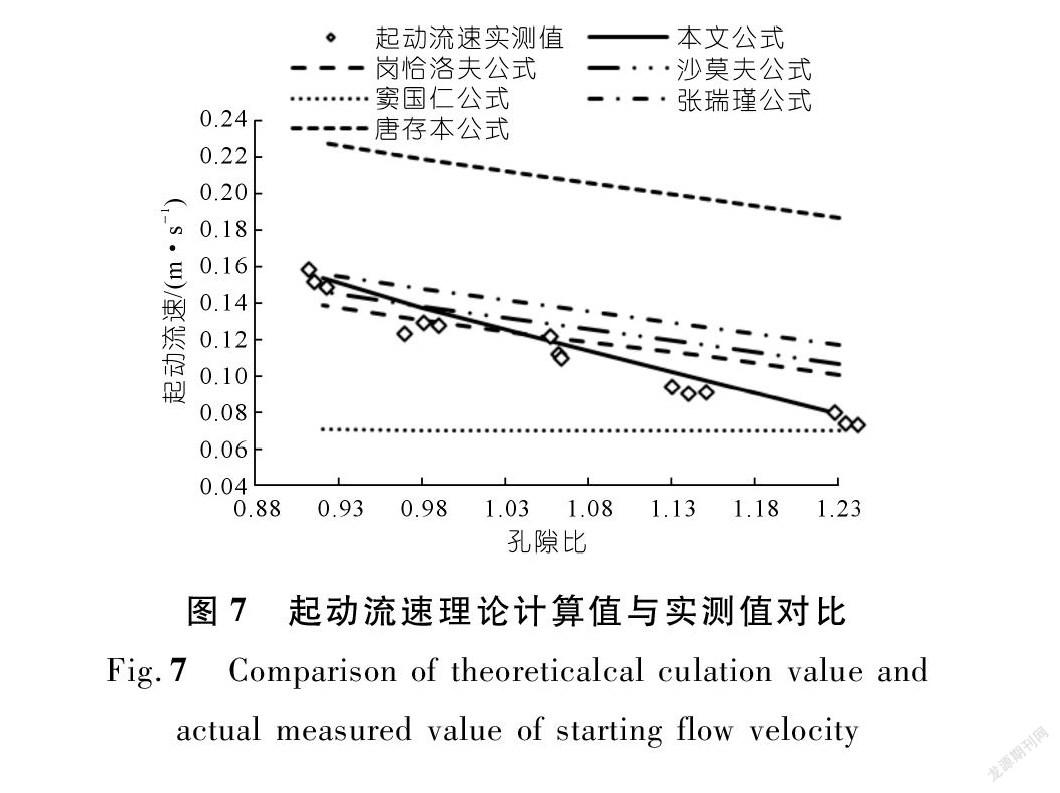
为进一步验证式（7）的可靠性，在保持内摩擦角不变的情况下，选取岗恰洛夫、窦国仁、唐存本、沙莫夫和张瑞瑾[13-17]提出的起动流速公式进行验证。

由图7可知，各公式的计算结果趋势大致相同，起动流速随孔隙比增加而降低，唐存本公式计算值相较实测值偏大，窦国仁公式中对起动流速影响因素考虑较多，本文试样的孔隙比最大相差仅为0.3，导致窦国仁公式的计算结果几乎为同一流速。相较于岗恰洛夫、张瑞瑾和沙莫夫公式的计算值，本文公式对小范围内孔隙比变化所计算的起动流速更加敏感。

2.3 起动切应力与孔隙比、内摩擦角的关系

在公式ΔB=KdΔtτ-τ01.5中，τ0代表无黏性砂的起动切应力，土的抗剪强度是抵抗水流冲刷的重要原因，土力学中采用库伦公式计算无黏性砂的抗剪强度：

τf=σtanφ（8）

式中：σ为剪切面上的法向应力;φ为内摩擦角;τf為抗剪强度。

但是，大量水槽试验结果表明土体起动时水流剪应力τ0比土体的抗剪强度τf小很多倍。土体起动时可能并未发生剪切破坏，大量学者进一步研究得到影响砂性土体起动的因素是土粒自重、土颗粒排列结构和土粒之间的咬合力。在当前的研究中对土粒之间咬合力难以测定且土颗粒的排列结构复杂多样，孔隙比e代表土体的密实程度，内摩擦角φ表示颗粒间摩擦力大小。试验证明试样越密实其所需的起动流速越大，本试验中用孔隙比和内摩擦角来量化起动指标。

根据明渠水流试验水流平均流速ū与摩阻流速u*的关系得：

ū=v0=5.75lg30.2yχksu*（9）

式中：ks为河床粗糙度，一般取ks=d，本文取ks=d50，mm;χ表示考虑黏性底层影响的修正系数，本文研究的无黏性砂，取χ=1;y为距床面的距离，m。

根据摩阻流速公式：

u*=τ0/ρ（10）

式中：τ0为起动切应力;ρ为液体密度，取水的密度ρ=1 g/cm3。

联立公式（9）～（10）得：

τ0=ū/5.052（11）

将公式（7）代入（11）得：

τ0=（-0.14e+0.023φ-0.445）/5.052（12）

化简得：

τ0=（-0.028e+4.6×10-3φ-0.09）2（13）

在相同粒径和水深条件下，本文将无黏性砂的咬合力和摩擦力对起动的影响具化为孔隙比e和内摩擦角φ对起动切应力τ0的影响，并得到起动切应力τ0与孔隙比e和内摩擦角φ的关系式，为无黏性泥沙的临界起动研究提供了新的思路。

2.4 水流流速对冲蚀的影响

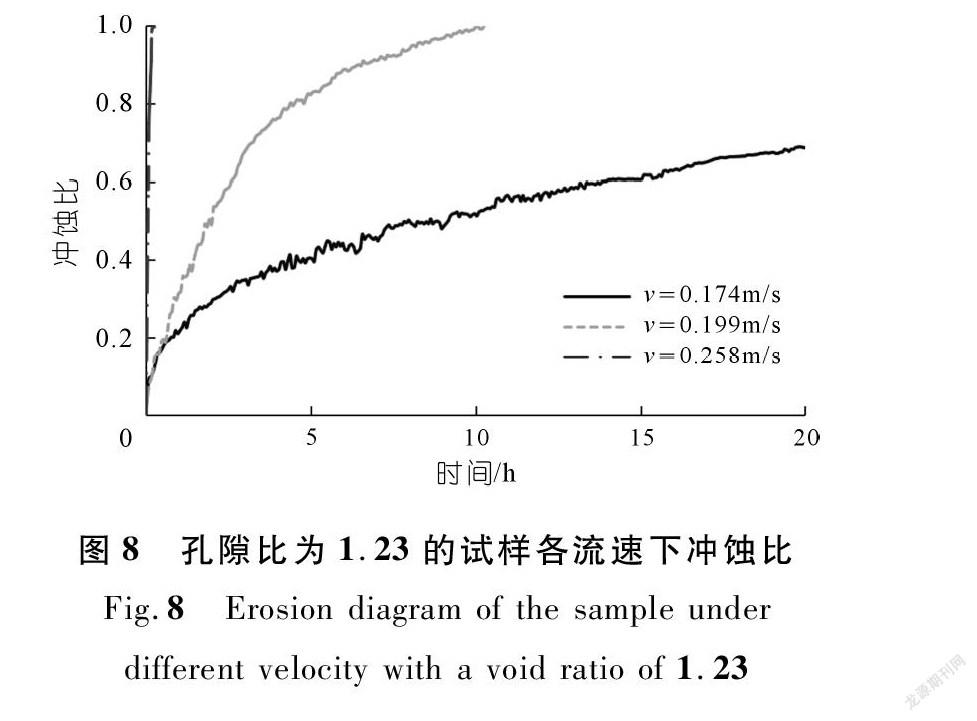
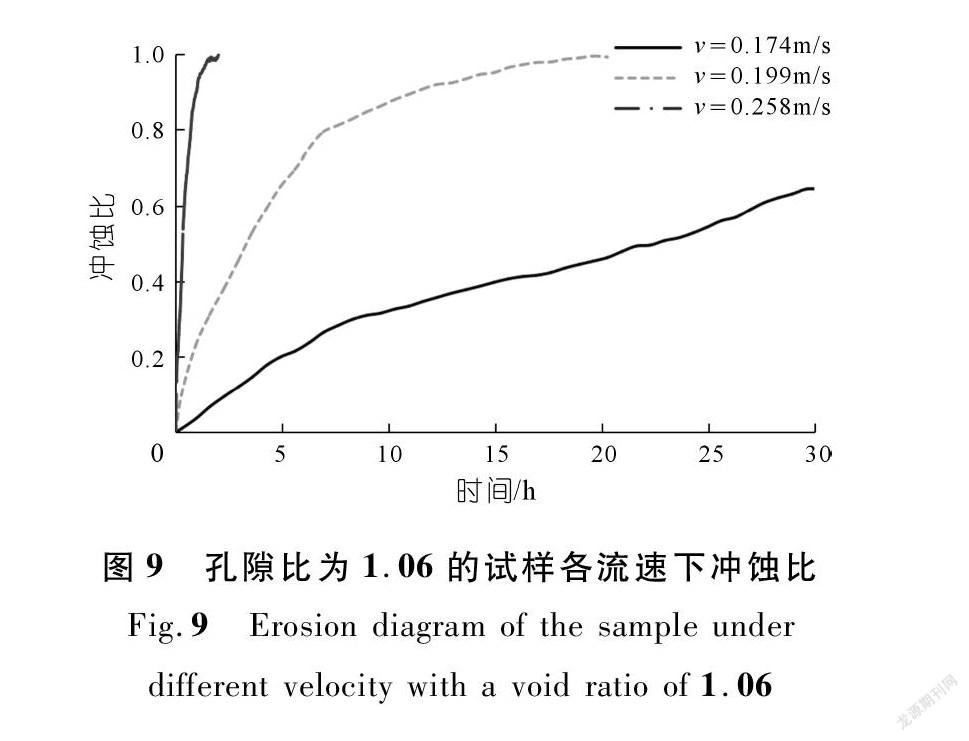
如图8～10所示，在相同孔隙比条件下，随着流速的增加，砂土的冲刷损失越来越快，土体的冲刷效果逐渐明显，但土体的冲刷损失速率与冲刷流速的关系逐步不明显。

在流速较低时冲蚀曲线呈现逐渐平滑的态势，在流速较高时不仅发展不平滑，且冲蚀曲线接近一条直线。该特性与实际情况一致，在流速比较低的情况下，水流流速是带走土颗粒的主要因素;在流速比较高的情况下，高速水流不仅是带走颗粒的主要因素，而且高速水流产生的较大剪力使土体产生剪切破坏，使大块的土体破坏流失。

在洪水季节水流流速急剧增大时，考虑增大岸坡的抗剪强度，是有效提高岸坡抵抗冲蚀破坏的方法。

2.5 孔隙比对冲蚀的影响

通过试验观察，无黏性砂的起动是以土颗粒形式的运动表现的。土样完全浸泡在浅水中，水压对土体的作用力微弱，相比于咬合力对土体起动的影响水压力的影响可以忽略不计。本试验采用的是同种土的饱和试样，控制其他因素相同，因而孔隙比是决定颗粒间咬合力的主要物理参数。

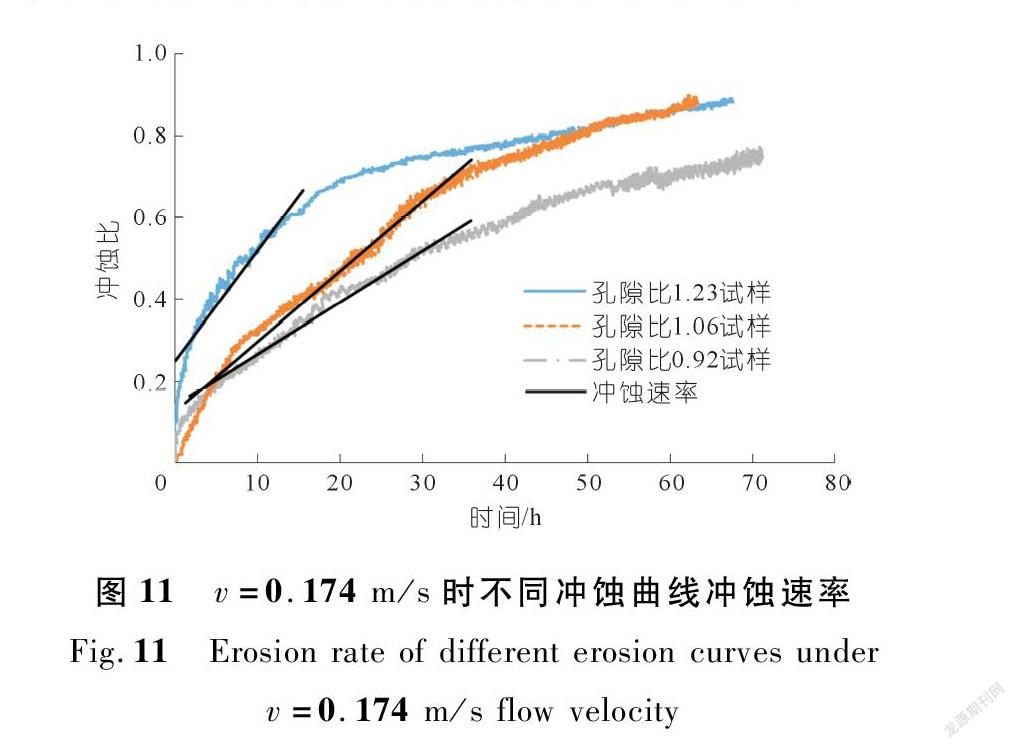
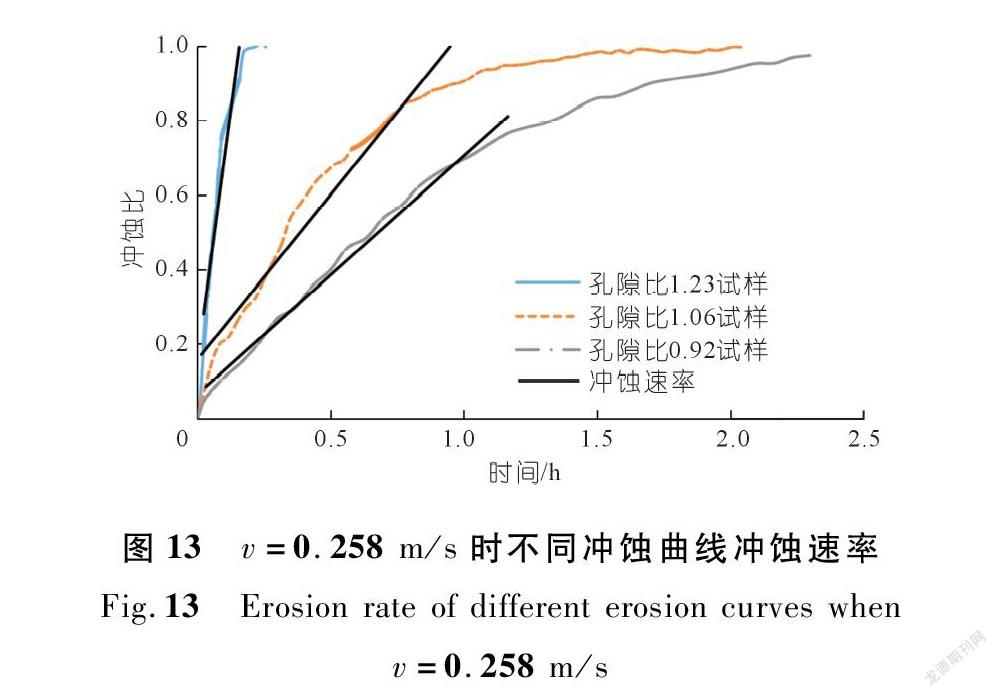
综合分析图11～13，可以发现每一组试样随着流速的增加其曲线的分散发展趋势相差不大，不同孔隙比的冲蚀曲线具有一定相似性。但是随着孔隙比的减小初始冲蚀率趋势发生变化，孔隙比对土体抗冲性能的影响体现出来，孔隙比为1.06，0.92的试样在v=0.174 m/s时，前10 h的抗冲刷能力明显优于孔隙比为1.23的试样，说明在相同土样中，孔隙比为1.23的试样土颗粒之间的咬合力大大降低。这种情况印证了在水流流速相同时较疏松的岸坡更易被冲蚀破坏。

2.6 无黏性砂可蚀性系数探究

无黏性砂的可蚀性系数Kd表现为冲蚀阶段的冲蚀速率，同一种无黏性砂，在不同的孔隙比和水流流速时表现出不同的冲蚀速率，不同冲蚀曲线之间存在一定相似性，证明无黏性砂的可蚀性系数是与孔隙比和水流流速相关的。为了进一步了解砂性土的可蚀性系数Kd，对各试样冲蚀曲线稳定段的冲蚀速率做对比分析。

公式（4）可化简为：

E=ΔB/B（14）

本文中E=εdΔt（15）

聯立得：ΔB=BεdΔt（16）

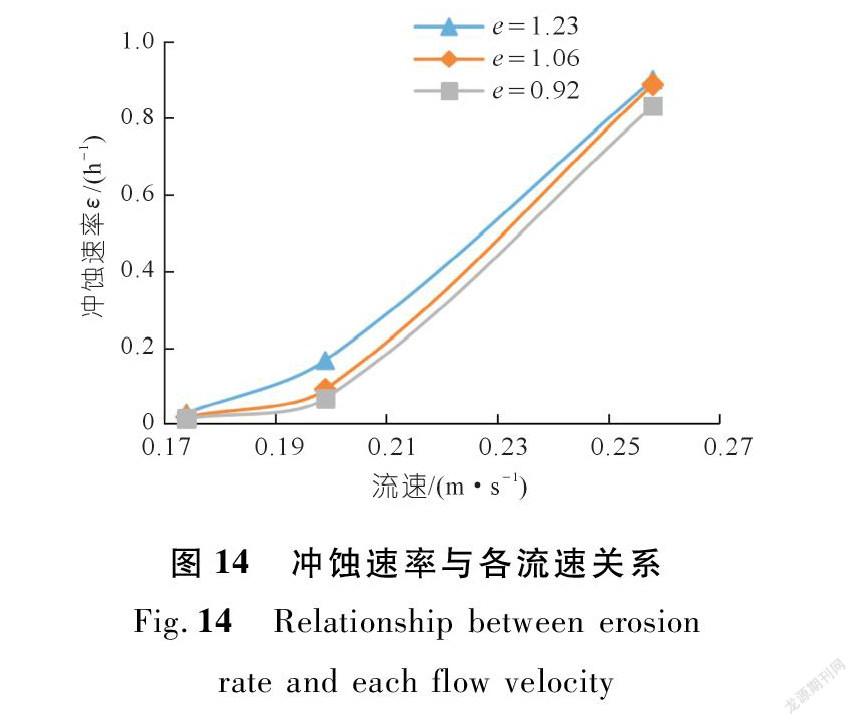
通过冲蚀稳定段的冲蚀速率进行对比，如图14所示，在孔隙比为1.23时，流速0.258 m/s的冲蚀速率明显的大于流速0.174 m/s和流速0.199 m/s的冲蚀速率，这表明同一孔隙比下冲刷流速越大，其冲蚀速率就越快，符合冲蚀模型公式的一般规律。

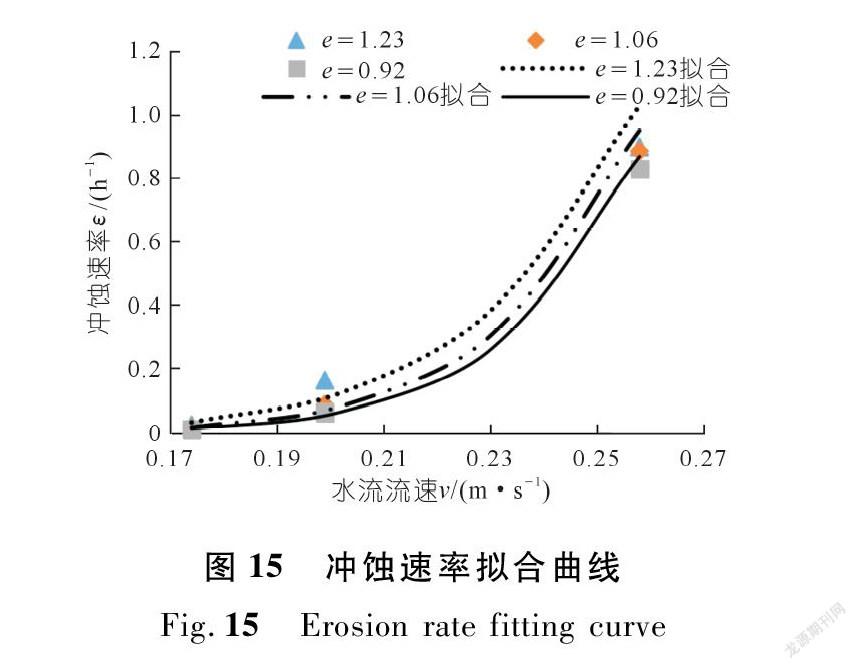
由图14可知，在v=0.174 m/s、v=0.199 m/s流速冲蚀下，试样的冲蚀速率增幅不大，试样的抗冲蚀能力并未发生变化，当水流流速增加到v=0.258 m/s时，不同孔隙比试样的冲蚀速率都呈现出一个陡增的态势，流速增加了20%，而冲蚀速率最大增加了30倍（见图15～16）。冲蚀速率εd与水流流速之间存在一定相关性，对关系曲线拟合得到：

εd=Aev10（17）

式中：Ae为土样系数。

对于无黏性砂的孔隙比，在本试验中没有得到冲蚀速率εd与e明确的函数关系，只是得到了两者之间存在正相关关系，结合

公式（16）得：

ε=Bεd（18）

可蚀性系数kd是表示土体冲蚀状态的重要指标，可表示为

kd=ε/τ-τ01.5（19）

如图17所示，不同孔隙比砂土的可蚀性系数kd与水流流速的关系表现一致，可蚀性系数kd随水流流速增加而增大且增加的速率表现出一定的规律性，最终得到：

kd=7v5.5+be（20）

式中：v表示水流流速，be为不同孔隙比砂土的土样系数。

ε和τ0的同时改变，导致了同流速下不同孔隙比砂土的可蚀性系数kd的be表现出差异性。

同一种土体的可蚀性系数kd与流速存在函数关系说明，同一岸坡无黏性砂的冲蚀是有规律可循的，但是冲蚀模型中Ae和be还是经验系数，并没有发现明确的规律，造成这一现象的原因是接来下需要进一步研究探索的课题。

3 砂性土冲蚀经验模型

经过冲蚀试验可获得可蚀性系数与水流流速的关系，见公式（20）。

将公式（20）代入到公式（2），得：

ε=7v5.5+be[τ-（-0.028e+4.6×10-3φ-0.09）2]1.5（21）

最终得到改进的无黏性砂河岸冲蚀公式：

ΔB=7v5.5+be[τ-（-0.028e+4.6×10-3φ-0.09）2]1.5Δt（22）

4 结 论

（1） 本文提出了新的起动流速测定方法，即目测观察和质量采集器相结合的方法，大大提高了无黏性砂起动流速的测量精度。

（2） 同种无黏性砂的起动流速和孔隙比成反比，起动流速与内摩擦角成正比，同一粒径和水深条件下可由孔隙比和内摩擦角计算无黏性砂的起动切应力。

（3） 同种饱和土体受水流冲蚀时的破坏形式相同，其抗冲刷能力随孔隙比的减小而增加;水流流速在起动流速以上时，冲刷流速越大土样冲刷流失就越快，且土体的损失由土颗粒流失变为水流剪切造成大量土体流失。

（4） 同种无黏性砂的冲蚀速率与流速的10次方成正比，可蚀性系数与水流流速的5.5次方成正比，随孔隙比增加而增加。

（5） 将孔隙比和内摩擦角作为影响河岸土体冲刷的内部因素，水流流速作为影响河岸土体冲刷的外部作用因素，具化了河岸土体冲刷特性的分析。在砂性土冲蚀模型基础上改进了冲蚀公式，使得冲蚀公式的参数更加明确。

参考文献：

[1] 汤明高.山区河道型水库塌岸预测评价方法及防治技术研究[D].成都：成都理工大学，2007.

[2] BRIAUD J L，CHEN H C，GOVINDASAMY A V，et al.Levee erosion by overtopping in New Orleans during the Katrina Hurricane[J].Journal of Geotechnical & Geoenvironmental Engineering，2008，134（5）：618-632.

[3] HANSON G J.Surface erodibility of earthen channels at high stresses part Ⅱ-developing an in situ testing device[J].Transaction of the Asae，1990，33（1）：127-131.

[4] DUNN I S.Tractive resistance of cohesive channels[J].Journal of Soil Mechanics and Foundation Division，ASCE，1959，85（3）：1-24.

[5] YALIN M S.Mechanics of sediment transport[M].Oxford：Pergamon Press，1972.

[6] MITCHENER H，TORFS H.Erosion of mud/sand mixtures[J].Coastal Engineering，1996，29（1-2）：1-25.

[7] OLSON T C，WISCHMEIER W H.Soil erodibility evaluation for soilsor the runoff and erosion stations[J].Soil Science Society of American，1963，27（5）：590-592.

[8] CHANDRA S，DE S K.A Simple laboratory apparatus to measure relative erodibility of soils[J].Soil Science，1978，125（2）：115-121.

[9] 鮑恩俣，熊康宁，刘子琦，等.喀斯特不同侵蚀场地土壤颗粒分布及可蚀性特征[J].森林与环境学报，2020，40（2）：156-163.

[10] 洪大林，张思和，高正荣，等.长江苏通公路大桥区原状淤泥质亚粘土起动试验研[J].水科学进展，2003，14（3）：345-349.

[11] 时连强，李九发，应铭，等.现代黄河三角洲潮滩原状沉积物冲刷试验[J].海洋工程，2006，24（1）：46-54.

[12] 李文杰，赵畅，杨胜发，等.三峡水库细颗粒泥沙起动流速研究[J].重庆交通大学学报（自然科学版），2016，35（6）：68-72.

[13] 张瑞谨.河流泥沙动力学[M].北京：中国水利水电出版社，1998.

[14] 窦国仁.再论泥沙起动流速[J].泥沙研究，1999（6）：1-9.

[15] 陈海英，尹家春，王费新，等.条子泥滩地粉细沙起动流速试验研究[J].水运工程，2015（6）：22-25.

[16] 钱宁，万兆慧.泥沙运动力学[M].北京：科学出版社，1991.

[17] 王文娥，廖伟，漆力健.宽窄相间河道水流紊动特性试验研究[J].水科学进展，2020，31（3）：394-403.

（编辑：黄文晋）

Improved experiment method for riverbank sand erosion and results analysis

CHEN Yong1，2，DONG Jinlong1，CUI Xiandong1 ，YE Runqing1，2

（1.Hubei Geological Disaster Prevention and Control Engineering Technology Research Center，China Three Gorges University，Yichang 443002，China; 2.Central South China Innovation Center for Geosciences，Wuhan 430205，China）

Abstract：

The erosion of riverbank sand has a great influence on the stability of the bank slope.It is difficult for traditional erosion instruments to conduct quantitative research on the soil initiation and erosion rate during the erosion process.A new type of erosion device for testing the erosion resistance of the soil was designed and produced.Based on the soil mass loss，the erosion state of the river bank was simulated.A mathematical model of soil erosion was established by a single variable starting test and erosion test.The results show that：① when the scouring rate of riverbank sand reaches 2×10-5～4×10-5 s-1，the starting velocity is reached.② The starting velocity is proportional to the void ratio and inversely proportional to internal friction angle.The starting shear stress can be expressed by void ratio and internal friction angle.③ The erosion rate of soil is positively correlated with void ratio and water flow velocity.④ The erodibility coefficient of the same kind of sandy soil is proportional to the 5.5 th power of the flow velocity.The erosion rate can directly reflect the erosion resistance of the river bank.

Key words：

starting velocity;starting shear stress;void ratio;water flow velocity;erosion rate