基于不同建模数据的陕西省志丹县滑坡易发性分区

王丽英 王红梅 郭盈盈 纪丁愈

摘要：滑坡易发性分区是预测滑坡的有效方法，但目前的建模数据较为单一，而建模数据会对分区的结果造成影响，因此，需要对建模数据源进行深入挖掘。以陕西省延安市志丹县为研究区，选择了10种滑坡诱发因子，基于289个滑坡样本，分别计算了各诱发因子的频率密度（FR）和盒维数，构建了2组差异化的建模数据;随后利用核函数逻辑回归模型（KLR）制作了研究区滑坡易发性分区图;最后采用平均绝对误差（MAE）和ROC曲线下的面积（AUC）对分区的结果和模型进行了评价和对比。结果表明：利用盒维数作为建模数据可有效提升分区结果的精度和模型的分类以及泛化能力，值得在研究区推广。

关 键 词：滑坡; 易发性分区; ROC曲线; 诱发因子; 频率密度; 盒维数; 志丹县; 陕西省

中图法分类号： P694

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.12.015

0 引 言

黄土滑坡是陕西省北部的黄土丘陵沟壑区范围内最具威胁的自然灾害之一，并且由于黄土本身的结构特性以及黄土高原特殊的自然环境，滑坡发生概率较高[1]。志丹县位于陕西省延安市西北部，地貌类型属于典型的黄土丘陵沟壑区，全县范围内地质灾害频发，根据志丹县2019年地质灾害防治方案显示，2019年内列入全县地质灾害群测群防数据库的隐患点共39处，其中滑坡22处，在每年在汛期时，都会发育大量的滑坡灾害，严重威胁当地居民的生产生活，制约着当地经济的发展。并且当地人口集中，加之资源和土地的需求量大，而地质灾害发育的范围仍在扩张，因此开展滑坡灾害的易发性分区工作十分必要。

对于滑坡易发性分区的研究，国内外学者不仅充分发挥了GIS技术在可视化分析、图形编辑、数据管理、空间分析、DEM模型等功能方面的优势，还先后提出了信息量模型[2]、专家打分模型[3]、逻辑回归模型[4]、判别分析模型[5]、人工神经网络模型[6]、支持向量机模型[7]、物元模型[8]等，基于不同的尺度开展了不同地区的滑坡易发性分区工作。虽然这些研究取得了丰硕的成果，但是在滑坡易发性分区建模的样本准备阶段，建模数据是影响易发性分区结果的关键因素[9]，而现有的研究所使用的建模数据较为单一，还未对不同类型的建模数据进行深入的挖掘和对比。

鉴于此，本文以志丹县作为研究区，分别基于两组差异化的建模数据集，构建核函数逻辑回归模型（Kernel logistic regression model，KLR），绘制研究区的滑坡易发性分区图。在评估易发性分区精度的基础上，对比评价建模数据对分区结果的影响。所得到的结果可以为当地地质灾害防治工作提供建议，同时也可以为黄土丘陵沟壑区的滑坡易发性分区研究提供一种新的方法。

1 研究区概况和数据来源

1.1 研究区概况

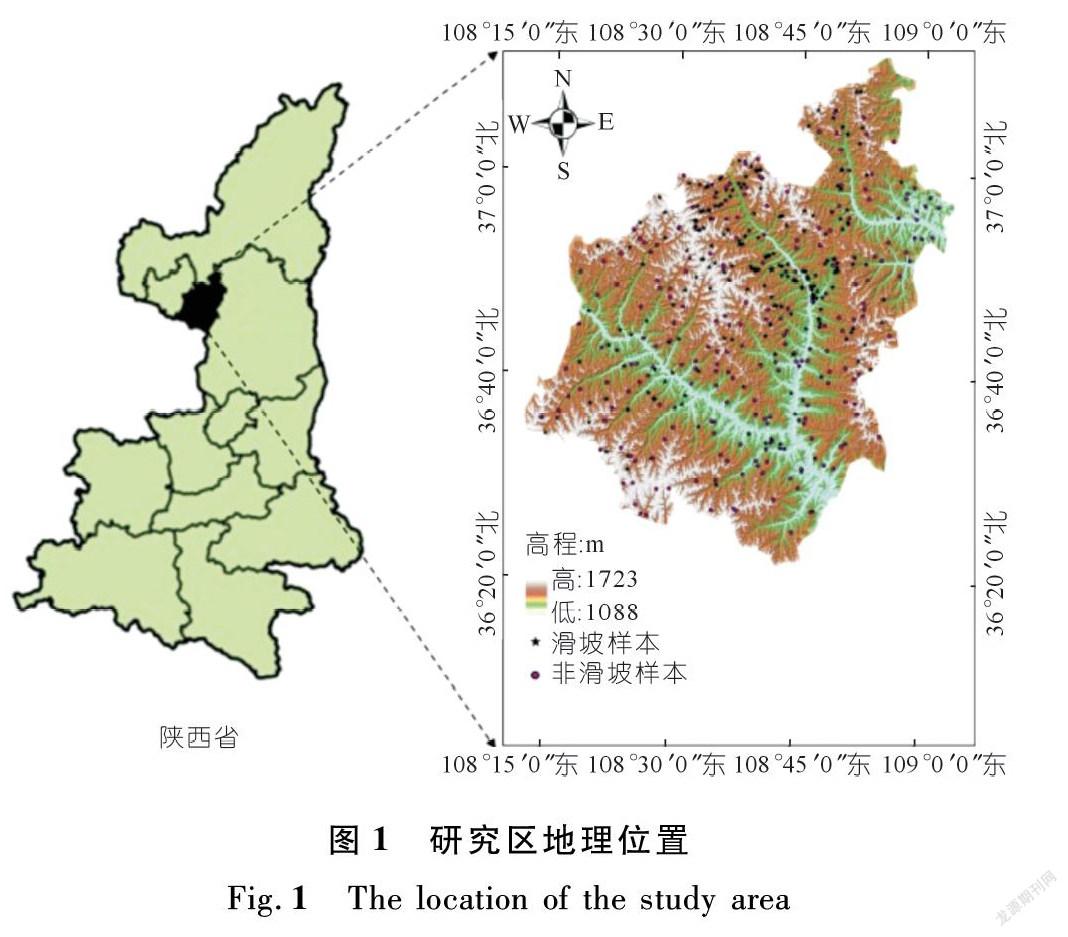
志丹县位于陕西省延安市西北部的黄土丘陵沟壑地区，地理坐标位于东经108°11′56″～109°3′48″，北纬 36°21′23″～37°11′47″之间（见图1）。全县东西长约70 km，南北宽约92.56 km，总面积约3 781 km2。志丹县的气候类型属于典型的温带大陆性季风气候，年平均气温为8.1 ℃，最低气温为-28 ℃，最高气温为37.4 ℃。由于志丹县地处黄土高原，年平均降雨量约为472.2 mm，降雨的月份在一年之中分布不均匀，6～8月为降雨相对集中的月份，降雨量约为292.9 mm，降雨通常以暴雨形式出现，占年降雨量的56%。降雨区域分布不均匀，总体趋势为从西北部地区到东南部地区降雨量逐渐增多，愈偏北降雨量愈少。流经志丹县境内的河流主要有洛河、周河、杏子河，县内以洛河、周河、杏子河3条河流为主干，大小支流、冲沟极为发育，沟壑密度为1.3 km/ km2，河流比降为1.6‰。

志丹县地貌类型属于以梁峁为主体的黄土梁峁丘陵沟壑区地貌，在长期的侵蚀作用下形成了几个显著的特点：地表破碎、梁峁密布、沟壑纵横、河谷深切、基岩裸露。全县范围内主要发育中生代-新生代地层，具体包括三叠系、侏罗系、新近系和第四系地层，其中第四系黄土覆盖于全县境内，其余时代的底层大多零星的出露于冲沟或者河谷两侧。根据地层年代将研究区的岩性类型划分为4组（见表1）。志丹县的地质构造类型属于华北陆台鄂尔多斯地台中的陕北盆地，构造类型是以延安地区为中心的陕北单斜翘曲构造，整体形状呈东高西低的趋势。据《陕西省区域地质志》记载[10]，志丹县境内无4级以上地震活动发生，所以本文研究的滑坡均为降雨型滑坡。

1.2 数据来源

本文所使用的原始数据包括：① 3.24 m×3.24 m分辨率的GF-2全色多光谱遥感影像（轨道号921309，日期2018-07-29）;②30 m×30 m分辨率的数字高程模型（DEM）;③ 1∶100 000比例尺的研究區土地利用图;④1∶200 000比例尺的研究区地质图;⑤ 基于野外实际调查的289个滑坡样本。

1.3 样本预处理

滑坡在遥感影像上所呈现出的平面形态是不规则的，由于受到研究区图幅比例尺的影响，当研究范围大于1 000 km2时，平面面积最大的滑坡在图中也无法显现出其全部的轮廓。并且在建模运算时，栅格图形分辨率的高低也会对模型运算的速度造成影响[11]。因此，对于滑坡易发性分区而言，有必要在建模前期对样本进行预处理。研究区内发育的滑坡总面积为30.24 km2，约占研究区总面积的0.8%。因此，为了提高运算效率，本文采用质心法（Centroid method）将研究区内289个不规则的滑坡图斑转换为289个滑坡点。

由于后续的滑坡易发性分区涉及到因子筛选和机器学习建模，而建立和评估模型的重点就是要将数据分别划分为训练样本集（Training dataset）和测试样本集（Validation dataset），所以需要创建与正样本（滑坡点）同等数量的负样本（非滑坡点），并按照7/3的比例对滑坡点和非滑坡点进行随机分割，最终得到由404个样本（202个滑坡点和202个非滑坡点）构成的训练样本集和由174个样本（87个滑坡点和87个非滑坡点）构成的测试样本集（见图1）。

1.4 诱发因子提取与分级

基于研究区的地质环境背景资料，选取了高程、平面曲率、剖面曲率、坡度、坡向、道路缓冲区、水系缓冲区、年平均降雨量、NDVI、地层岩性作为研究区滑坡诱发因子。随后利用ArcGIS软件，基于所选用的数据源对诱发因子进行提取，并将因子图层全部重采样为30 m×30 m分辨率（见图2）。最后对提取出的诱发因子进行分级。

2 研究方法

2.1 FR的计算方法

利用频率密度（Frequency ratio，FR）量化滑坡诱发因子是一种较为常用的方法。

通常以Sim/S表示诱发因子各分级内的滑坡样本数（Sim）占总样本数（S）的百分比，以Zim/Z表示诱发因子各分级的栅格数（Zim）占总栅格数（Z）的百分比，利用公式（1） 可计算得出各诱发因子分级对应的FR。

FR=Sim/SZim/Z（1）

随后，基于计算得到的FR值，分别对每一种滑坡诱发因子进行重分类，构建出基于FR的建模数据集1。

2.2 分维数的测量方法

分维数是定量反映功能、形态、时间、信息、空间等特征在局部与局部、局部与整体之间具有统计意义的参数，也可以定量反映滑坡的空间分布特征[12]。为了测量研究区滑坡在空间内分布的分形维数，本文采用目前应用最广泛的分维数测量方法，即盒维数法（Box-counting Method）。盒维数法是既可以在二维、三维空间中进行分维数估算的经典方法，同时也适用于点集[13]。

盒维数的测量原理为：首先利用边长为γ的正方形对分割研究区，统计包含滑坡点的网格数N（γ），不断改变γ对研究区重新划分，统计有滑坡点分布的网格数量，从而获得点对序列（γ，N（γ））。按照1 m的间隔改变γ 50次，使得点对序列满足或者近似满足公式（2），则可计算出对应的盒维数d。

Nγ=γ-d（2）

同样的，基于测算出的盒维数，分别对每一种滑坡诱发因子进行重分类，构建出基于盒维数的建模数据集2。

2.3 诱发因子优选

在滑坡易发性分区建模的过程中，并不是所有的滑坡诱发因子都对模型有积极的贡献[14]。因此，为了提高模型运算的精度和效率，有必要对诱发因子进行筛选。本文通过计算各诱发因子对应的信息增益率（Information gain ratio，IGR）来完成因子筛选。

熵可以反映滑坡诱发因子在评价体系中的混乱程度，而信息增益率是通过构建C4.5决策树，定量测算各诱发因子的熵增速率，从而判断诱发因子对滑坡易发性分区模型的贡献程度。IGR的输出范围为[0，1]，当诱发因子的IGR为0时，表明该因子对模型无贡献，需要排除，且不参与建模。

2.4 KLR模型简介

KLR模型的原理是在传统逻辑回归模型的基础上，利用核函数（Kernel Function）将研究区内的滑坡点转换至一个n维空间内，使得线性不可分的问题得以在高维空间中被解决。KLR模型的计算方法如下：

LogitP=w·φx+b（3）

这里灾损土地发生的可能性同样用P表示，w和b是模型的两个参数，φ为核函数，则公式（3） 的对数形式可以写为

P=11+exp（w·φx+b）（4）

本文所使用的核函数为RBF核函数，其表达式如下：

Kxi，xj=exp-δxi-xj2，δ>0（5）

这里δ控制着RBF核函数的敏感度，在计算时需要手动输入。

2.5 模型对比和结果评估的方法

2.5.1 统计学指标

滑坡易发性分区结果的精度会对后续滑坡的防治工作造成影响，因此有必要对分区的结果进行评估。本文利用平均绝对误差（Mean Absolute Error，MAE）来对易发性分区的精度进行检测[15]。MAE表示所有独立样本的观测值与目标值之间的偏差，可以定量反映实际预测误差的大小，MAE越小，说明结果的精度越高。

MAE=1nnz=1Az-F（z）（6）

式中：n为滑坡样本点的数量，z表示滑坡样本点，A（z）和F（z）分别表示观测值和目标值。

2.5.2 ROC曲线

本文利用受试者接收特征曲线（Receiver Operating Characteristic Curve，ROC）对滑坡易发性分区模型进行比较。ROC曲线在滑坡易发性分区研究中应用十分广泛，同时也取得了令人满意的效果[16]。ROC曲线的横轴和纵轴分别为1-特异度（1-Specificity）和敏感度（Sensitivity），通常利用曲線下面积（AUC）来判定模型的优劣[17]。AUC的计算方法如下：

Sensitivty=TPTP+FN（7）

Specificity=TNTN+FP（8）

AUC=TP+TNTP+TN+FP+FN（9）

式中：TP和TN分别表示被正确分类的滑坡点和非滑坡点的数量，FN和FP分别表示被错误分类的滑坡点和非滑坡点的数量。一般来讲，AUC越接近1，说明模型的分类能力越强。

3 结果与分析

3.1 因子筛选结果

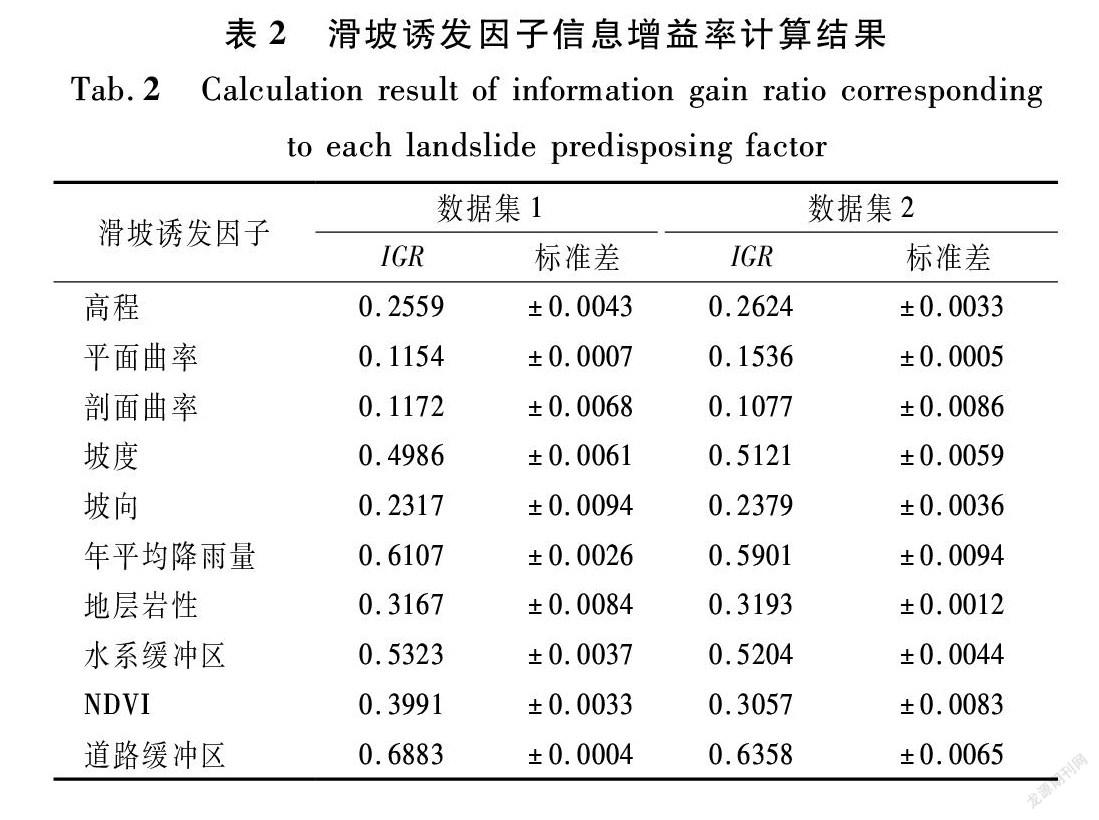
基于数据集1和数据集2中的训练数据，分别计算数据集中各滑坡诱发因子对应的IGR。从表2可以看出，在数据集1和数据集2中，道路缓冲区因子对模型的贡献度都最高，IGR值分别为0.688 3和0.635 8;数据集1中得平面曲率因子对模型的贡献度最低（IGR为0.115 4），数据集2中的剖面曲率因子对模型的贡献度最低（IGR为0.107 7）。此外，研究区内所有滑坡诱发因子的IGR值均大于0，且对应的标准差均处于合理的范围内，表明所有的诱发因子都对模型有积极的贡献。因此，保留数据集1和数据集2中的全部滑坡诱发因子。

3.2 基于差异化建模数据的滑坡易发性分区

基于表3所列出的FR以及盒维数，构建了数据集1和数据集2。分别利用数据集1和数据集2中的训练数据训练KLR模型。为了对模型中的参数进行优调，本文采用10折交叉验证（10-Cross Validation）的方法分别获得了数据集1对应的参数（δ=0.025 2）和数据集2对应的参数（δ=0.027 1）。

分别利用数据集1和数据集2构建KLR模型，模型输出的后验概率即为滑坡易发性指数（Landslide susceptibility index，LSI），输出区间为[0，1]。LSI越趋近于1，说明滑坡发生的概率越高，反之亦然。随后基于自然间断点法将两组LSI分割为5个区间，分别代表极低易发区、低易发区、中易发区、高易发区和极高易发区。最后利用ArcGIS软件对划分后的易发区进行可视化，结果如图3所示。

3.3 分区结果精度评价

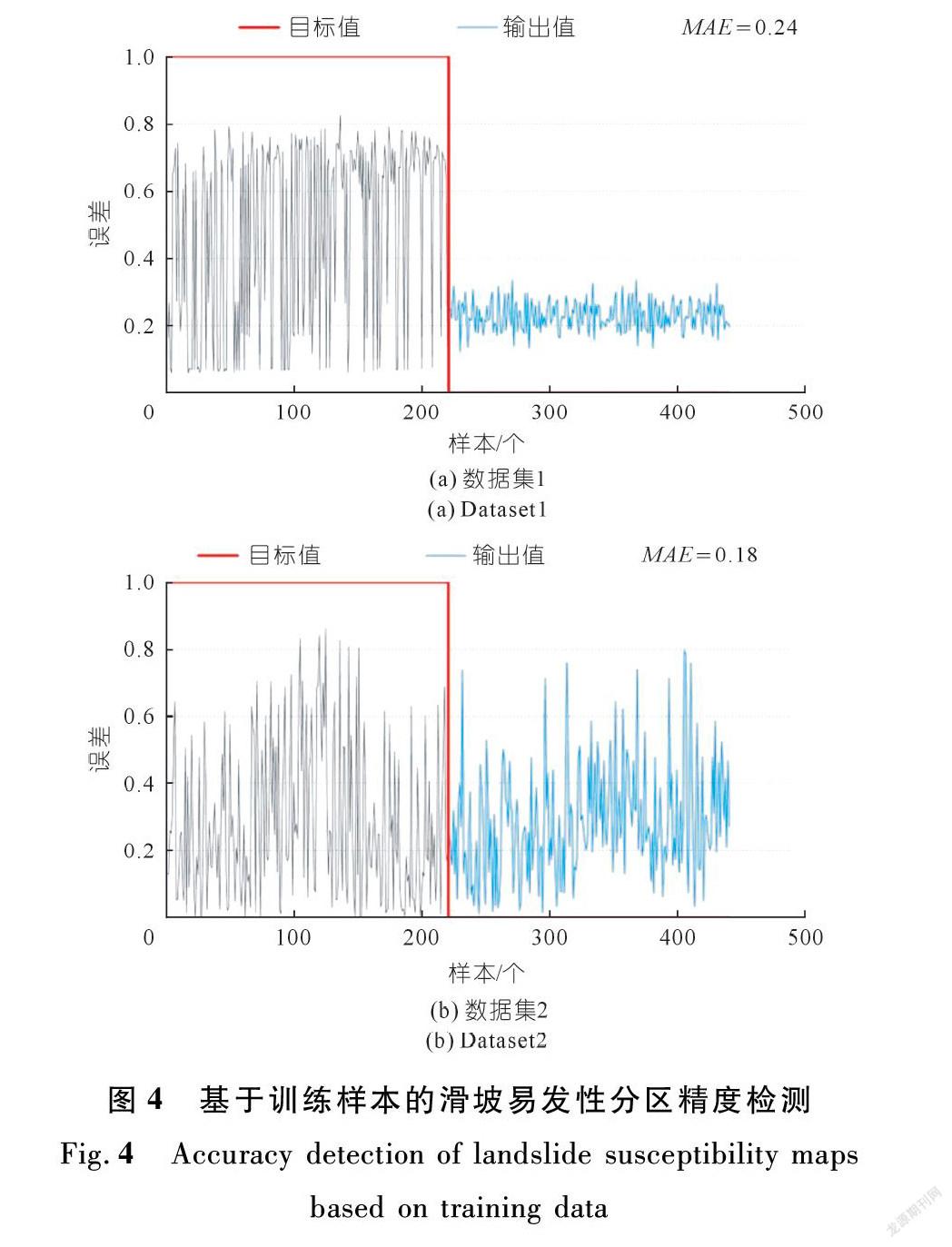
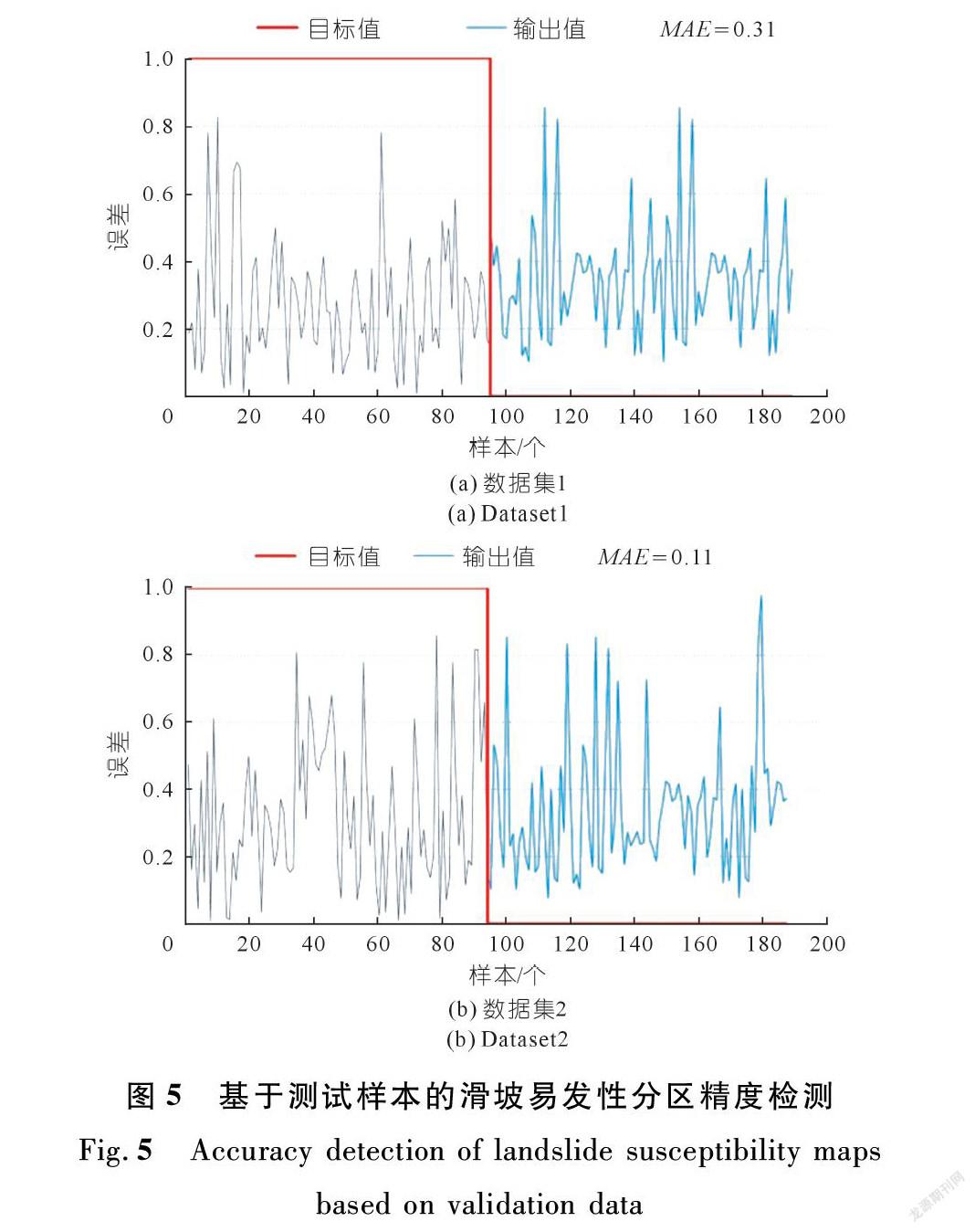
本文分别利用数据集1和数据集2中的训练数据和测试数据，计算分区结果对应的MAE来完成精度评价。从训练数据检测的结果可以看出（见图4）：基于数据集1所构建的KLR模型的MAE=0.24，基于数据集2所构建的KLR模型的MAE=0.18。从测试数据检测的结果可以看出（见图5）：基于数据集1所构建的KLR模型的MAE=0.31，基于数据集2所构建的KLR模型的MAE=0.11。结果表明，利用数据集2作为建模数据生成的滑坡易发性分区结果的精度高于数据集1。

3.4 模型对比

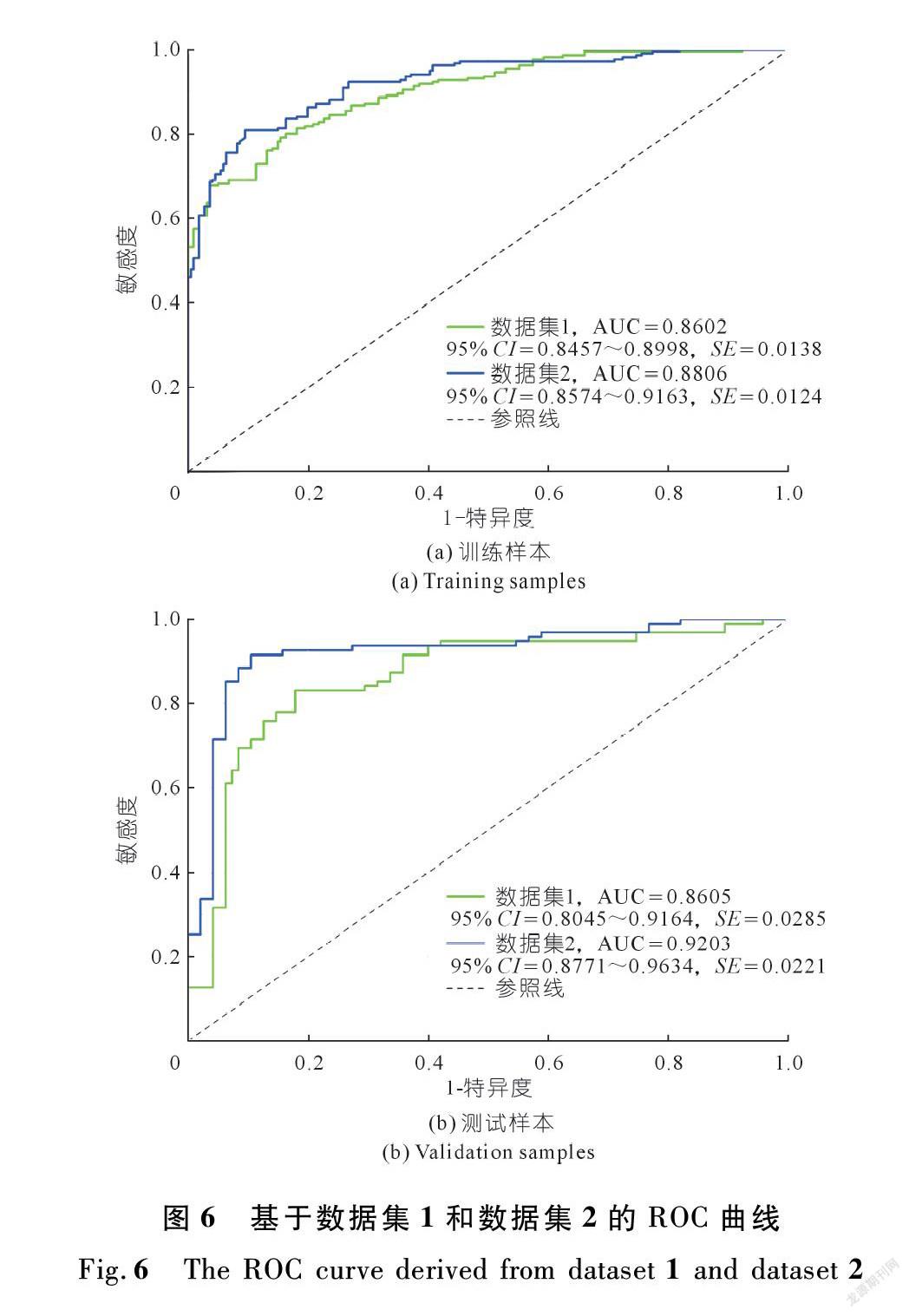
本文利用ROC曲线下的面积（AUC）对比模型的分类能力和泛化性。分别基于数据集1和数据集2中的训练数据绘制ROC曲线，见图6（a），结果显示数据集2对应的AUC值最高为0.880 6，并且95% CI和标准差均最低，表明利用数据集2构建的KLR模型对滑坡的分类能力最强。

分别基于数据集1和数据集2中的测试数据绘制ROC曲线，见图6（b），结果显示数据集2对应的AUC值同样最高为0.920 3，且95% CI和标准差均最低，表明利用数据集2构建的KLR模型的泛化性最优，值得在研究区推广。

4 讨 论

在滑坡易发性分区建模前，排除无贡献程度的因子是非常必要的[18]。众多研究结果表明：如果利用对模型无贡献的诱发因子参与建模，不仅会降低运算效率，增加过拟合的风险，同时也会对分区结果的精度造成影响[19-20]。因此本文通过计算信息增益率来定量评估滑坡诱发因子对模型的贡献程度，排除无贡献的诱发因子，以保证分区结果的精度。

KLR模型是基于LR模型衍生出的一種高性能机器学习算法，具有结构简单等优点。KLR模型不仅在滑坡灾害的研究中被广泛使用，同时也在其他的研究领域被使用[21]。在构建KLR模型的过程中，参数的选择直接决定着分类的精度[22]。因此本文利用了10折交叉验证的方法进行调参，目的就是为了将参数对模型的影响降至最低。另外，选择不同的核函数也会产生不同的结果，鉴于此，在今后的研究中，会尝试利用不同的核函数来完成滑坡易发性分区，并对结果进行评估。

利用FR作为模型的建模数据，在滑坡研究中十分常见，但是利用盒维数作为KLR模型的建模数据的研究还少之又少。从张庭瑜等[23-24]的研究可以看出，在县域尺度下，盒维数不仅可以有效地反映出滑坡在空间中的分布状态，同时也可以揭示滑坡诱发因子与滑坡之间的内在联系。另外从结果可以明显看出，利用盒维数作为模型的建模数据，可以取得更高精度的分区结果，同时，模型的分类能力和泛化性也优于传统建模数据。因此，认为利用盒维数作为滑坡易发性分区的建模数据是一种高效且新颖的方法。

5 结 论

本文分别利用频率密度和盒维数量化滑坡诱发因子，构建了2种差异化的建模数据集（数据集1和数据集2）。以核函数逻辑回归模型（KLR）和289个滑坡样本为基础，分别利用两种数据集构建了KLR模型，制作了陕西省延安市志丹县滑坡易发性分区图。利用平均绝对误差（MAE）和ROC曲线下的面积（AUC）对分区的结果和模型进行了评价。结果表明：当利用盒维数作为建模数据时，滑坡易发性分区结果的平均绝对误差最小（MAE=0.11），精度最高，且模型对滑坡的分类能力最强，泛化性最优。同时所得到的结果可以为当地的滑坡防治工作提供数据基础，也可以为今后研究区内的滑坡研究提供参考。

参考文献：

[1] 徐张建，林在贯，张茂省.中国黄土与黄土滑坡[J].岩石力学与工程学报，2007，17（7）：1297-1312.

[2] 张向营，张春山，孟华君，等.基于GIS和信息量模型的京张高铁滑坡易发性评价[J].地质力学学报，2018，34（1）：96-105.

[3] 张向营，张春山，孟华君，等.基于Random Forest和AHP的贵德县北部山区滑坡危险性评价[J].水文地质工程地质，2018，45（4）：142-149.

[4] TSANGARATOS P，ILIA I.Comparison of a logistic regression and Nave Bayes classifier in landslide susceptibility assessments：the influence of models complexity and training dataset size[J].Catena，2016，145（2）：164-179.

[5] 李秀珍，王成华，宋刚.基于Fisher判别分析法的潜在滑坡判识模型及其应用[J].中国地质灾害与防治学报，2009，20（4）：23-26.

[6] CHEN W，POURGHASEMI H R，ZHAO Z.A GIS-based comparative study of Dempster-Shafer，logistic regression and artificial neural network models for landslide susceptibility mapping[J].Geocarto International，2017，32（4）：367-385.

[7] KUMAR D，THAKUR M，DUBEY C S，et al.Landslide susceptibility mapping & prediction using Support Vector Machine for Mandakini River Basin，Garhwal Himalaya，India[J].Geomorphology，2017，295（15）：115-125.

[8] 吴益平，殷坤龙，姜玮.浙江省永嘉县滑坡灾害风险预警研究[J].自然灾害学报，2009，18（2）：124-130.

[9] JUNG-HYUN L，SAMEEN M I，PRADHAN B，et al.Modeling landslide susceptibility in data-scarce environments using optimized data mining and statistical methods[J].Geomorphology，2018，303（9）：284-298.

[10] 陕西省地质矿产局.陕西省区域地质志[M].北京：地质出版社，1989.

[11] HYUN-JOO O，SARO L，SOO-MIN H.Landslide susceptibility assessment using frequency ratio technique with Iterative random sampling[J].Journal of Sensors，2017，2017（4）：1-21.

[12] YANG Z Y，POURGHASEMI H R，LEE Y H，et al.Fractal analysis of rainfall-induced landslide and debris flow spread distribution in the Chenyulan Creek Basin，Taiwan[J].Journal of Earth Science，2016，27（1）：151-159.

[13] LIU L，LI S，LI X，et al.An integrated approach for landslide susceptibility mapping by considering spatial correlation and fractal distribution of clustered landslide data[J].Landslides，2019，16（4）：1-14.

[14] HONG H，PRADHAN B，SAMEEN M I，et al.Improving the accuracy of landslide susceptibility model using a novel region-partitioning approach[J].Landslides，2018，15（4）：753-772.

[15] PHAM B T，PRAKASH I，SINGH S K，et al.Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques：hybrid machine learning approaches[J].Catena，2019，175（5）：203-218.

[16] 韓玲，张庭瑜，张恒.基于IOE和SVM模型的府谷镇滑坡易发性分区[J].水土保持研究，2019，26（3）：373-378.

[17] 张庭瑜，韩玲，张恒，等.混合分类模型在滑坡易发性分区中的适用性研究：以延安市宝塔区为例[J].干旱区资源与环境，2020，22（1）：192-201.

[18] YOUSSEF，AHMED M，AL-KATHERY，et al.Landslide susceptibility mapping at Al-Hasher area，Jizan（Saudi Arabia）using GIS-based frequency ratio and index of entropy models[J].Geoscience Journal，2015，19（1）：113-134.

[19] KAVZOGLU T，KUTLUG SAHIN E，COLKESEN I.An assessment of multivariate and bivariate approaches in landslide susceptibility mapping：a case study of Duzkoy district[J].Natural Hazards，2015，76（1）：471-496.

[20] YOUSSEF A M，POURGHASEMI H R，POURTAGHI Z S，et al.Landslide susceptibility mapping using random forest，boosted regression tree，classification and regression tree，and general linear models and comparison of their performance at Wadi Tayyah Basin，Asir Region，Saudi Arabia[J].Landslides，2016，13（5）：839-856.

[21] CHEN W，XIE X，PENG J，et al.GIS-based landslide susceptibility modelling：a comparative assessment of kernel logistic regression，Nave-Bayes tree，and alternating decision tree models[J].Geomatics Natural Hazards & Risk，2017，8（2）：950-973.

[22] WANG L J，SAWADA K，MORIGUCHI S.Landslide-susceptibility analysis using light detection and ranging-derived digital elevation models and logistic regression models：a case study in Mizunami City，Japan[J].Journal of Applied Remote Sensing，2013，7（1）：35-61.

[23] ZHANG T Y，HAN L，HAN J，et al.Assessment of landslide susceptibility using integrated ensemble fractal dimension with Kernel Logistic Regression Model[J].Entropy，2019，21（2）：218-234.

[24] ZHANG T Y，HAN L，ZHANG H，et al.GIS-based landslide susceptibility mapping using hybrid integration approaches of fractal dimension with index of entropy and support vector machine[J].Journal of Mountain Science，2019，16（6）：1275-1288.

（編辑：刘 媛）

Landslide susceptibility mapping based on differentiated modeling data in Zhidan County，Shaanxi Province

WANG Liying1，WANG Hongmei2，GUO Yingying1，JI Dingyu3

（1.School of Intelligent Construction，Chongqing Vocational College of Civil Engineering，Chongqing 400072，China; 2.Urban Construction College，Chongqing Energy Vocational College，Chongqing 402260，China; 3.State Key Laboratory of Hydraulics and Mountain River Development and Protection，Sichuan University，Chengdu 610065，China）

Abstract：

Landslide susceptibility mapping is an effective method to predict landslides，but the current modeling data is relatively single，moreover the modeling data may affect the results of the mapping.Therefore，it is necessary to dig deeper into the modeling data sources.In view of this，we selected 10 landslide triggering factors in Zhidan County，Yanan City，Shaanxi Province.Based on 289 landslide samples，the frequency ratio and box counting dimension of each triggering factor were calculated，and two sets of differentiated modeling data were constructed.Then，the landslide susceptibility maps of the study area were made by using the kernel function logistic regression model.Finally，the average absolute error （MAE） and the area under the ROC curve （AUC） were used to evaluate and compare the results of landslide susceptibility mapping.The results show that using the box dimension as the modeling input data can effectively improve the accuracy of the partition results and the classification and generalization capabilities of the model，which is worthy of promotion in the study area.

Key words：

landslide;susceptibility mapping;ROC curve;landslide triggering factors;frequency ratio;box counting dimension;Zhidan County;Shaanxi Province