气候变化条件下降雨-融水型泥石流流量预测方法
2021-01-16杨宗佶付校龙游勇
杨宗佶 付校龙 游勇















摘要:全球气候变化背景下,目前唯一的冰川泥石流流量经验模型无法定量反映雨热耦合变化的影响。根据度日模型冰雪融水当量和泥石流流量雨洪计算方法,提出了考虑雨热耦合条件下降雨-融水型泥石流流量的计算模型。通过统计51 a降雨和温度观测资料的变化趋势,建立了帕隆藏布流域降雨-融水型泥石流流量计算重现期标准,并通过对典型降雨-融水型泥石流流量的实测资料进行验证,表明该方法准确性相比经验模型明显增加。进一步以帕隆藏布流域15条典型降雨-融水型泥石流为例,开展气候变化条件下泥石流流量的计算和预测。结果显示:该方法可量化雨热耦合条件对泥石流流量的影响,可为气候变化条件下冰川泥石流的防治关键参数计算和预测提供参考依据。
关 键 词:降雨-融水型泥石流; 泥石流流量; 度日模型; 雨热耦合变化; 气候变化; 帕隆藏布流域
中图法分类号: P642.23
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2021.12.006
0 引 言
冰川泥石流广泛分布于中国青藏高原[1-2]及世界各地的高山地区[3-5]。随着全球气候变暖,冰川消融加剧[6],将导致冰川泥石流频繁发生。国内外对冰川泥石流展开的相关研究主要是成灾条件和机理方面。对于冰川泥石流的形成过程,部分学者认为冰碛物在其中发挥了重要作用[7-8],还有学者认为冰川泥石流的形成是复合过程[9],并将其启动过程总结为侵蚀-滑移型[10]。对于冰川泥石流的形成条件,前人认为其暴发与水热组合关系密切,且多发生在湿热环境下[1,11];还有部分学者研究认为其起动和起动方式与气温上升下冰川融水[12-13]、黏粒含量[14]以及初始含水率[15]有关。但是目前有关冰川泥石流流量的计算方法的研究较少,只有一套中科院成都山地所提出的经验公式[16],无法反映温度和降雨两个关键因素对冰川泥石流流量的影响。因此本研究以帕隆藏布流域为研究区域,以降雨与气温[17]为关键参数,构建了叠加小流域暴雨洪水计算公式和改进度日模型[18-20]的降雨-融水型泥石流流量的计算模型和预测方法,为气候变化背景下冰川泥石流的工程防治关键参数的选取和预测预报提供了新的方法。
1 研究方法
雨热耦合条件下降雨-融水型泥石流流量的计算方法分别考虑全流域的降雨量和冰雪流域的冰雪融水当量。
1.1 改进冰雪融水当量计算方法
全流域24 h内冰雪的消融水当量M1根据冰雪消融与气温之间关系建立的度日模型[18-20]进行计算:
M1=DDF·T24(S1F)(1)
式中:T24为一天的平均气温,℃,考虑冰雪区域不同海拔位置的气温梯度,T24=T-(ELE-2 736)×0.47[21];S1为冰雪融水面积,km2;DDF为冰川或雪的度日因子,mm/(d·℃)。
改进的度日模型是在刘金平等[22]拟合的公式基础上进行了改进,考虑了坡度的影响,由于冰雪的消融和其与空气的接触面积密切相关[23],不同坡度投影面积下冰雪区域与空气的接触面积不同,因而改进公式如下:
DDF=(0.009×ELE-0.934×LAT-8.1)×cosθ(2)
式中:ELE代表海拔高度,m;LAT代表纬度,(°);θ为冰雪融水区域以上范围的平均坡度,(°)。
1.2 降雨-融水型泥石流流量计算
(1) 改进算法。
改进《四川省中小流域暴雨洪水计算手册》中的计算公式,叠加融水和降雨量,求得全流域在降雨-融水条件下的洪水洪峰流量。
Q=0.278(H24+M1)24n-1τn-μF(3)
式中:Q为洪水洪峰流量,m3/s;H24是全流域降雨量,采用24 h降雨量的统计数值,mm;M1为24 h融水量,mm;n为暴雨参数;τ为流域汇流时间,h,τ=0.278LmJ1/3Q1/4[24];m为汇流参数;J为流域平均纵比降;μ为平均下渗强度,mm/h;F为全流域面积,km2。
本文采用配方法计算泥石流的峰值流量,其计算公式为
Qc=(1+φc)QDu(4)
φc=γc-γwγs-γc(5)
式中:Qc为泥石流洪峰流量,m3/s;φc为泥石流洪峰流量修正系数;Du为堵塞系数;γc为泥石流容重,t/m3;γw为清水比重,t/m3;γs为泥石流中固体物质比重,t/m3。
(2) 传统算法。
目前唯一能考虑冰川泥石流流量计算的经验模型是由中科院成都山地所提出的经验公式[16]:
Qc=(Q2+Q0)(1+φc)d(6)
式中:Q0为流域内非冰川区的洪峰流量,m3/s;Q2为降雨型冰川消融流量,m3/s,Q2=F1(0.05H+2.1),H为降雨量,mm;d为冰川消融洪峰系数,d=1+7.6(F1/F)+0.05θ0;F1为冰川面积,km2;θ0为冰川坡度,(°)。
2 数据来源
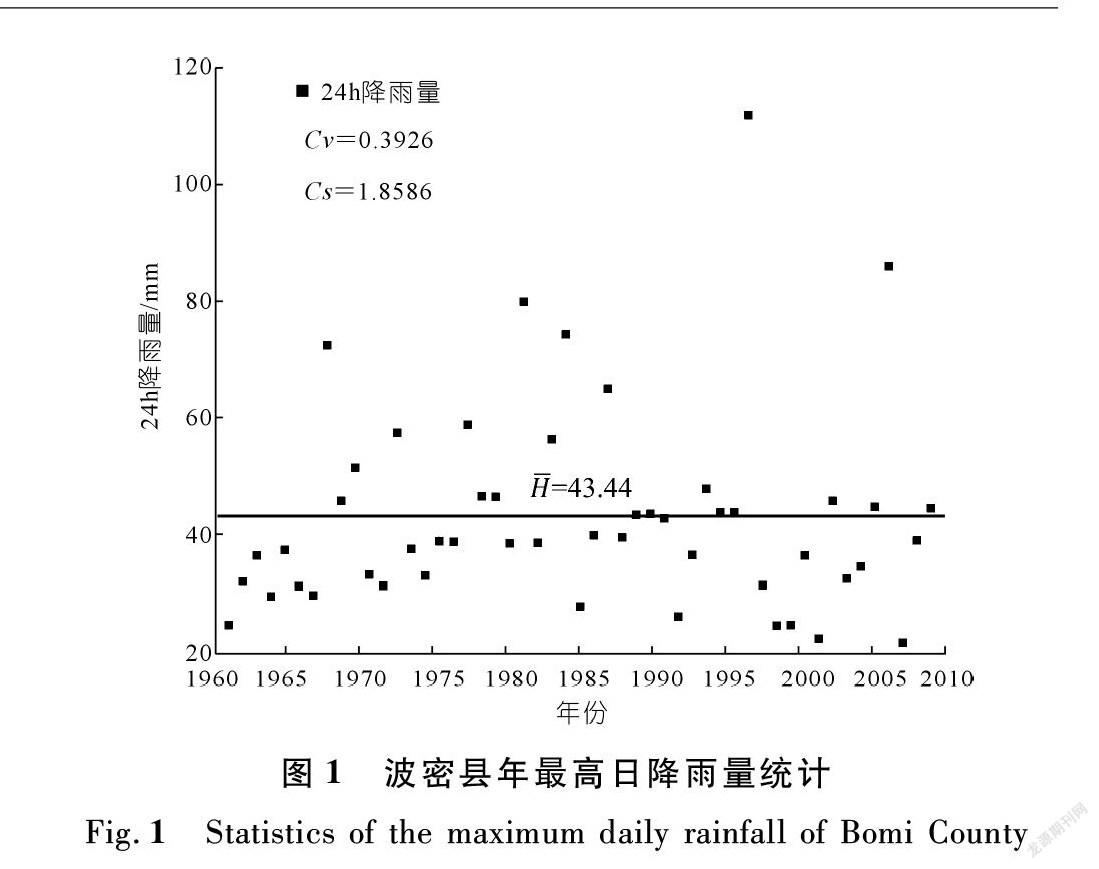
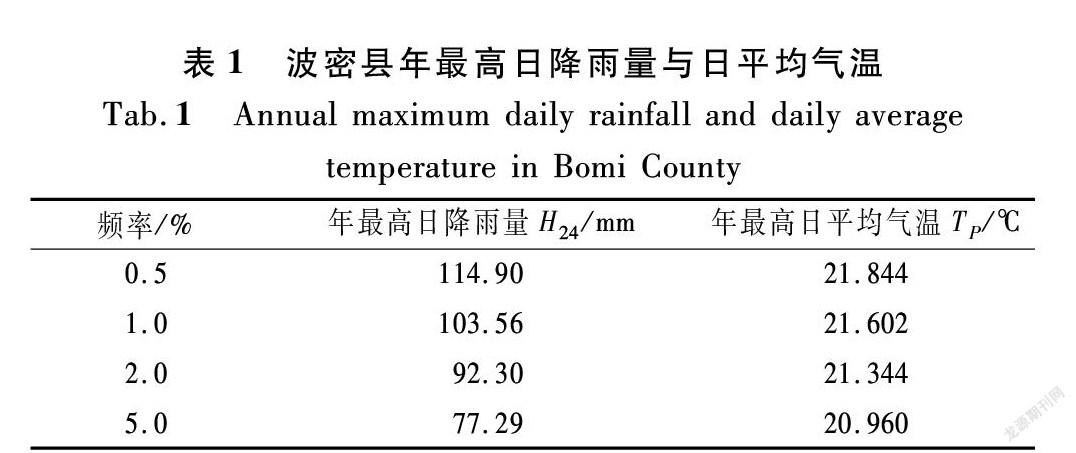
帕隆藏布流域是中国最典型的海洋性冰川区和雅鲁藏布江降水中心且具有雨热同期的特点,升温和暴雨成为诱发大型泥石流的有利条件。本文对波密县1961~2011年51 a的降雨和气温数据通过皮尔逊-Ⅲ型曲线进行概率分析统计计算(见图1~2),在皮尔逊-Ⅲ型曲线的分析中得到在不同频率下年最高日平均气温以及日降雨量如表1所列。
由于波密县的气温呈现整体上升的趋势,因此將这51 a的日最高平均气温拟合如图2所示,在对2011年以前的泥石流实例验证中的温度指标减去了这个升温趋势,公式为TPa=TP-0.03612×(2011-a);TPa为第a年频率为P的年最高日平均气温,℃;TP为波密县统计不同频率年最高日平均气温,℃;a为年份。对以后泥石流的预测则是在不同情景条件下叠加升温趋势,公式为TPn=TP+0.03612×n,TPn为n年一遇的年最高日平均气温,℃。
3 模型验证
本文选取了帕隆藏布流域前期研究和实测数据相对较丰富的古乡沟和培龙沟两条典型冰川泥石流开展实例验证(见图3)。历史统计数据如表2所列。
通过皮尔逊-Ⅲ型曲线计算不同频率下的温度TP以及TPa得到1983,1984年和2005年的不同频率下的最高日平均气温如表3所列。
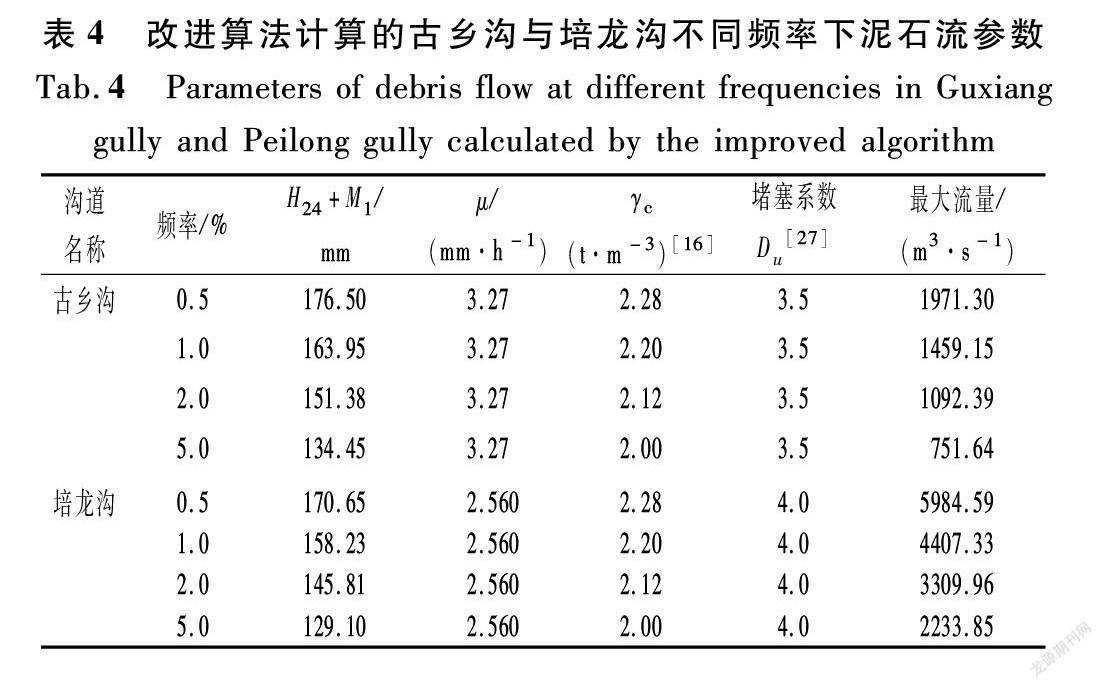
通过改进算法和传统算法计算古乡沟与培龙沟不同频率下的泥石流数据如表4~5所列。
改进算法和传统算法在不同频率下计算得到的古乡沟和培龙沟泥石流流量与实测数据对比如图4~5所示。
如表2~3所列,以温度为衡量指标,古乡沟2005年约为27 a一遇的泥石流,由改进算法求得的流量为831.33 m3/s,与前人[25]计算的33 a一遇的泥石流规模849.65 m3/s比较符合。以温度为衡量指标,培龙沟1983年和1984年的泥石流频率分别为36 a一遇和154 a一遇,由改进算法求得的流量分别为2 808 m3/s与5 259 m3/s,与历史记载流量2 950 m3/s与5 245 m3/s相似度较高。而由图4~5和表4~5对比分析可知,传统算法的计算结果普遍偏大,改进算法对古乡沟和培龙沟的计算准确性相比传统方法分别提高47.26%与21.12%~32.5%。
根据历史资料揭示,古乡沟泥石流的规模在1953年以后在逐渐减小,且20世纪70年代以后泥石流流量都普遍小于1 000 m3/s[28],而传统经验算法计算古乡沟20 a一遇流量达1 156 m3/s,严重偏大,相比之下改进算法精度更高。
4 气候变化条件下泥石流预测
4.1 波密地区泥石流沟基本数据
本文选择了15条典型降雨-融水型泥石流沟进行气候变化条件下泥石流流量预测(见图3),基础数据如表6所列。
4.2 波密地区泥石流冰雪消融量
波密地区的泥石流冰雪融水当量采用度日模型公式(1) 进行计算。以表1的不同频率下的年最高日平均气温为标准,叠加最近51 a升温趋势下的日平均气温与降雨量,如表7所列。计算得到的全流域24 h冰雪融水当量如表8所列。
4.3 波密地区泥石流沟计算结果
结合全流域24 h冰雪融水量和降雨量,通过传统算法(式(6))和改进算法(式(3)、(4))计算不同頻率下泥石流沟的泥石流流量的结果如表9和图6所示。
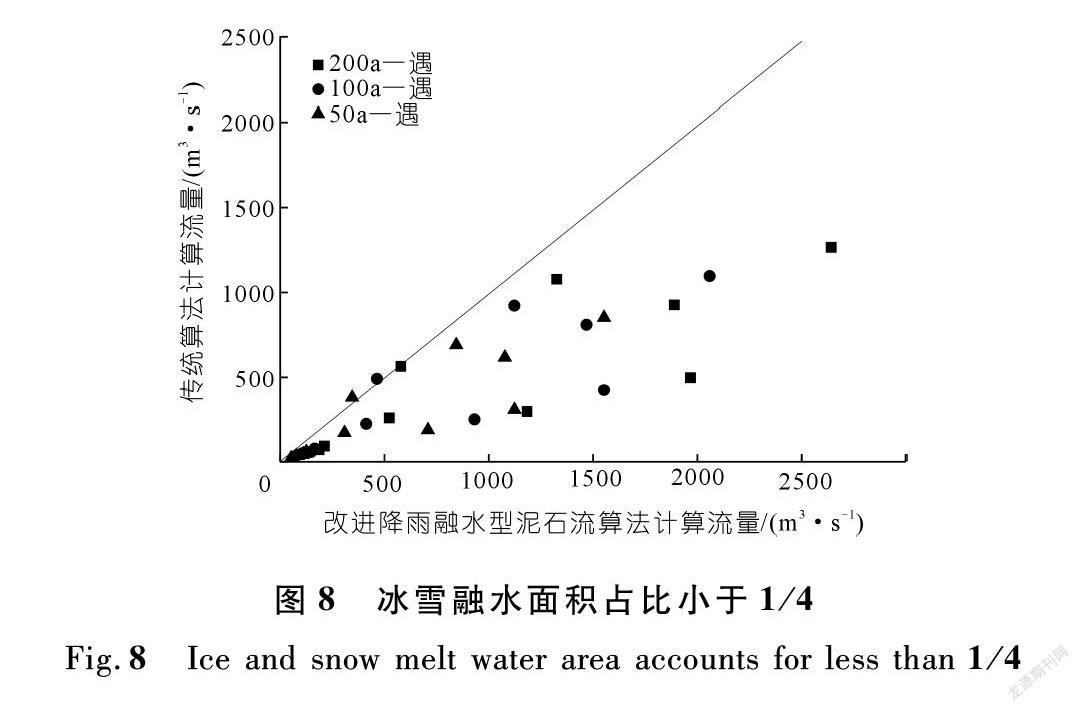
将上述15条泥石流沟按冰雪融水面积占全流域面积大于1/4和小于1/4分为两类(见图7和图8)。
由上述图表可知,传统经验算法的计算结果很大程度上取决于冰川区域,在冰川面积占比大于1/4的区域(见图7),改进算法的计算结果稍低于偏向保守的传统算法。而在冰川面积占比小于1/4的区域(见图8),传统算法计算的结果则远小于改进算法,因而在冰川占比较小的区域,传统算法的结果则会过于偏小。而现如今冰川的面积在逐年减少[29],所以相比传统依赖于冰川面积的经验算法,改进算法在今后预测气候变化条件下泥石流流量的实用性和准确性更强。
5 结论和讨论
(1) 建立了降雨-融水型泥石流温度频率确定标准,构建了波密地区气候变化条件下的升温趋势,提出了基于改进的度日模型和雨洪法的改进降雨-融水型泥石流流量算法。
(2) 以古乡沟和培龙沟为例,改进算法的结果与历史数据对比,误差分别为2.24%与0.27%~4.85%,准确性比传统经验模型提高了47.26%与21.12%~32.5%。
(3) 对于冰川占比大于1/4的4条沟,传统算法与改进算法误差在3%~20%之间,由于传统算法较为保守,因此传统算法的结果均大于本文的改进算法,所以传统的经验算法对于冰川面积占比大于1/4的泥石流流域仍然具有不错的参考价值。但是对于冰川面积占比较小的泥石流沟,计算结果则会偏低甚至无法作为参考,因此改进算法适用性更广。
(4) 本研究在用度日模型计算冰雪融水的时候叠加了波密县近51 a来的升温趋势,使预测结果更加符合气候变化的趋势。
参考文献:
[1] 吕儒仁,李德基.西藏波密冬茹弄巴的冰雪融水泥石流[J].冰川冻土,1989,11(2):148-160.
[2] GE Y G,CUI P,SU F H,et al.Case history of the disastrous debris flows of Tianmo Watershed in Bomi County,Tibet,China:some mitigation suggestions[J].Journal of Mountain Science,2014,11(5):1253-1265.
[3] JACKSON L E,HUNGR O,GARDNER J S,et al.Cathedral Mountain debris flows,Canada[J].Bulletin of Engineering Geology and the Environment,1989,40(1):35-54.
[4] WILKERSON F D,SCHMID G L.Distribution of debris flows in Glacier National Park,Montana,U.S.A.[J].Journal of Mountain Science,2008,5(4):318-326.
[5] HUGGEL C,HAEBERLI W,KAAB A,et al.An assessment procedure for glacial hazards in the Swiss Alps[J].Canadian Geotechnical Journal,2004,41(6):1068-1083.
[6] 何秋乐,匡星星,梁四海,等.1966~2015年长江源冰川融水变化及其对径流的影响:以冬克玛底河流域为例[J].人民长江,2020,51(2):77-85,130.
[7] 施雅风,杨宗辉,谢自楚,等.西藏古乡地区的冰川泥石流[J].科学通报,1964,9(6):542-544.
[8] 杜榕桓,章书成.西藏高原东南部冰川泥石流的特征[J].冰川冻土,1981,3(3):10-16.
[9] FLEISCHMAN C M.Debris Flow[M].Beijing:Science Press,1985.
[10] RUOFU S.Basic characteristics and measuring method of debris flow[M].Chongqing:Science and Technology Literature Press Chongqing Branch,1986.
[11] 齐云龙,邓明枫.川藏公路波密段九绒沟泥石流形成机制研究[J].灾害学,2019,34(3):123-127.
[12] 陈晓清,崔鹏,杨忠,等.聂拉木县冲堆普2002年泥石流成因分析及防治对策[J].冰川冻土,2006,28(5):776-781.
[13] ZIMMERMANN M,HAEBERLI W.Climatic change and debris flow activity in high-mountain areas:a case study in the Swiss Alps[J].Catena Supplement,1992,22(1):59-72.
[14] 陈宁生,王政,田树峰,等.冰碛土体起动泥石流的特征研究[J].第四纪研究,2019,39(5):1235-1245.
[15] 潘蕾,魏学利,张远芳,等.初始含水率对冰川泥石流的起动影响分析[J].水土保持学报,2017,31(6):116-122.
[16] 罗德富,毛济周.川藏公路南线(西藏境内)山地灾害及防治对策[M].北京:科学出版社,1995.
[17] 屈永平,肖进,潘义为.藏东南地区冰川泥石流形成条件初步分析:以天摩沟冰川泥石流为例[J].水利水电技术,2018,49(12):180-187.
[18] SINGH P,KUMAR N,ARORA M.Degree-day factors for snow and ice for Dokriani Glacier,Garhwal Himalayas[J].Journal of Hydrology,2000,235(1):1-11.
[19] HOCK R.A distributed temperature-index ice-and snowmelt model including potential direct solar radiation[J].Journal of Glaciology,1999,45(149):101-111.
[20] HOCK R.Temperature index melt modelling in mountain areas[J].Journal of Hydrology,2003,282(1/4):104-115.
[21] 鄧明枫.帕隆藏布流域冰川降雨型泥石流频发成因分析[D].北京:中国科学院大学,2019.
[22] 刘金平,张万昌.雅鲁藏布江流域度日因子空间变化[J].中国科学院大学学报,2018,35(5):131-138.
[23] HOCK R.Glacier melt:a review of processes and their modelling[J].Progress in Physical Geography,2005,29(3):162-391.
[24] 熊文华,孙立霞,李诚,等.澜沧江与怒江流域洪峰流量公式推求[J].人民长江,2020,51(11):82-86.
[25] 鲁安新,邓晓峰,赵尚学,等.2005年西藏波密古乡沟泥石流暴发成因分析[J].冰川冻土,2006,28(6):956-960.
[26] 程尊兰,吴积善.西藏东南部培龙沟泥石流堵塞坝的形成机理[A].第八届海峡两岸山地灾害与环境保育学术研讨会[C]∥乌鲁木齐:中国水土保持学会,2011:39-45.
[27] 国家防汛总指挥部办公室,中国科学院水利部成都山地灾害与环境研究所.山洪泥石流滑坡灾害及防治[M].北京:科学出版社,1994.
[28] 朱平一,罗德富.西藏古乡沟泥石流发展趋势[J].山地学报,1997,15(4):296-299.
[29] 刘时银,姚晓军,郭万钦,等.基于第二次冰川编目的中国冰川现状[J].地理学报,2015,70(1):3-16.
(编辑:刘 媛)
Discharge prediction method for rainfall-melting water triggered glacial debris flows under climate change scenarios
YANG Zongji1,FU Xiaolong1,2,YOU Yong1
(1.Institute of Mountain Hazards and Environment,CAS,Chengdu 610041,China; 2.University of Chinese Academy of Sciences,Beijing 100049,China)
Abstract:
Under the background of global warming,current empirical model for the glacial debris flow discharge calculation cannot quantitatively consider the coupling effect of rainfall water and the snow/ice melting water.We proposed a discharge calculation model that considers coupling effect of both rain and melting water for glacial debris flows by studying ice-snow melt equivalent in the improved degree-day model as well as the current storm flood calculation method for rainfall triggered debris flows.The criteria of return period for the glacial debris flows discharge prediction was established based on the rainfall and temperature change trends fitted by the 51 years long period observation data in the Palong Zangbo watershed.Then this proposed model was verified by the observation data of 2 typical glacial debris flows along the Palong Zangbo River,and the accuracy of the proposed method was significantly improved by comparing to the current empirical model.Afterwards,the discharge estimation of 15 glacial debris flow gullies in the Palong Zangbo watershed were analyzed under various climate change scenarios.The results show that the proposed method can quantify the coupling effect of rain-thermal on debris flow and can provide a reference for the calculation and prediction of key parameters for the prevention and control of glacial debris flows.
Key words:
rainfall-melting water debris flows;debris flows discharge;degree-day model;rain-thermal coupling changes;climate change;Palong Zangbo watershed
