让操作真正成为学习理解深入的利器

胡娴

[摘  要] 实践操作是小学生数学学习的重要拐杖，更是他们建构认知、发展思考力的重要抓手。为此，在小学数学教学活动活动中，教师要密切关注操作实验活动的组织与思考，使之更有利于学习观察、学习思考、学习合作等顺利发生，也有助于数学思维的发展，真正成为有效数学学习的利器。

[关键词] 操作;数学;学习;理解;深入

诗意江南，古都秋韵。也正是在这美好的盛景中，我有幸参加了江苏省《全国苏教版小学数学教材第五届优秀课评比暨课堂教学观摩》活动，其间聆听了大师们智慧、精彩的教学示范课，也欣赏了各地选手的精美展示课。二十一节课宛如古都金陵，有隽永的文化底蕴，又有清新的现代气息，令人思绪翩翩，回味无穷。其中一位老师执教的“三角形三边的关系”一课中学生的实践操作活动，给我些许触动，使我产生了一丝联想，生发了点滴思考。在此，截取教学片段，并粗浅地谈谈自己的思考。

师：通过刚才的研究，我们认识了三角形，那下面的图形哪些是三角形，哪些不是？为什么呢？

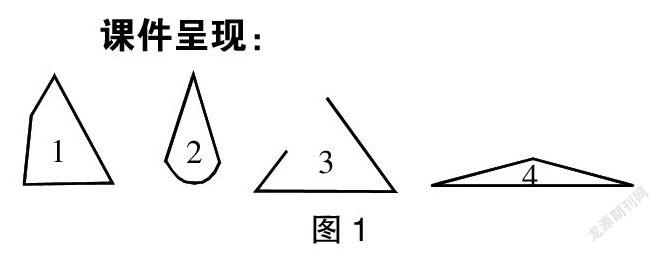
课件呈现：

生1：图1不是三角形，因为它有4条边。

生2：图2也不是，因为它有一条边是弯的。

生3：图3不是，因为它没有围成。

生4：图4是，因为它的3条线段是首尾相接的。

……

师：总结得很棒！那么是不是所有的三条线段都能围成三角形呢？有15厘米、10厘米、8厘米、5厘米四根小棒，猜猜会有什么样的可能呢？

学生汇报猜想：10厘米、8厘米、5厘米，15厘米、10厘米、8厘米，10厘米、5厘米、15厘米，15厘米、8厘米、5厘米。

师：这都是猜想，对不对呢？实践是检验真理的唯一标准，下面就让我们就用实践来验证一下吧！

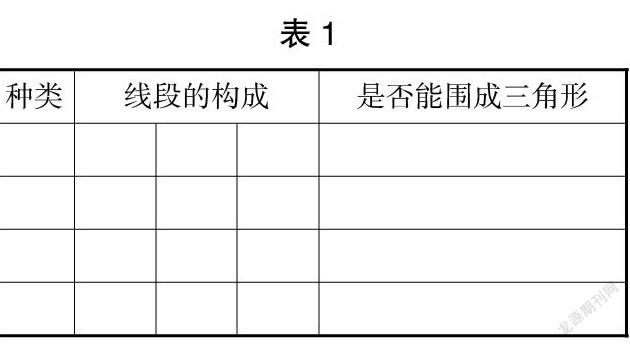
学生小组活动，利用学具盒中的四个小棒，进行合作学习研究。完成练习纸上的表格。

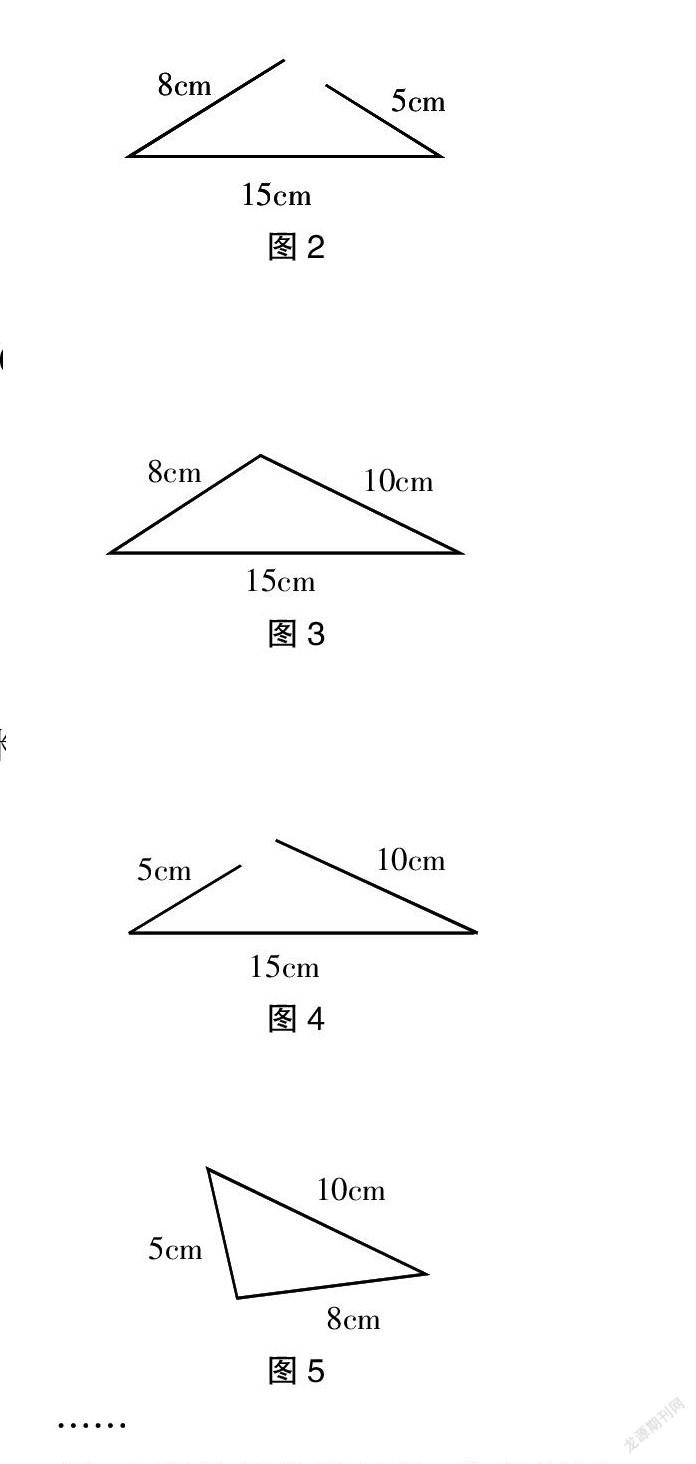
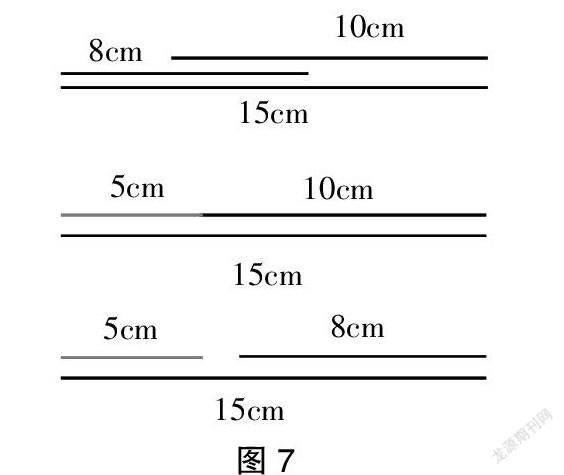
生1：我们小组选用了15厘米、8厘米、5厘米，发现不能围成三角形。展示操作结果：

生2：我们选择的是15厘米、8厘米、10厘米，能围成三角形。展示操作结果：

生3：我们用5厘米、10厘米、15厘米围的，没有首尾相接。展示操作结果：

生4：用10厘米、5厘米、8厘米能围成三角形。展示操作结果：

……

师：大家的操作很具体，你能通过实践发现围成的三边之间有什么特征吗？不能围成的呢？

生：三条边比较接近的线段，是可以围成三角形的。

生：两条边的和等于第三条边，是没法围成三角形的。

生：如果有两条边的和还比第三条边小的话，也是不可以围成三角形的。

生：我感觉，要围成三角形就得保证有两条边的和大于第三边。

生：不对吧！如10厘米、5厘米、15厘米的小棒，就有两条边的和大于第三条边，但是它却没围成一个三角形。

师：这个举例很科学，那我们从中会获得怎样的新的思考呢？

……

思考：截取这个教学片段，旨在让同仁们体味其中学生实践操作过程，反思这一实践操作学习活动是否有助于学生感知“三角形三边之间的关系”，是否能起到促进学习感悟的深入，助力学习的推进，利于学生获得正确的、深刻的表象等功效。也粗浅地谈谈在该过程中教师应如何科学解读教材文本、灵活进行活动指导和学习方向掌控的一点思考。

1. 紧扣“围成”促思考

本节课教学的落脚点是：吃透“三角形”的要义，理解隐含在字里行间的本质属性，并以此开启实践操作的智慧之门。什么是三角形呢？百度百科上呈现的定义是：由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫作三角形。从中对教师来讲就得认真解读“首尾顺次连接”，案例中教师对此环节的引领是扎实的，也是到位的。用“围成”揭示了这一连接的基本属性，体现了三角形三边构成的必要条件。

然而，笔者粗浅地以为，对“围成”的解读和实践可以更深入点，使之更加务实点，对学生的理解和深化提供更翔实的感知和表象。如，用塑料管或细铁丝、钉子板和橡皮筋等教学具，围一围三角形，让学生真正体验围成的构造，在真实“围图”活动中体会到“围”的本质，明白“围图”是无缝隙的，也是无间隙的。进而，对首尾相接的理解会伴有更多的思维成分，体验会愈加深刻。

给学生具体的活动任务，让他们在钉子板上围一围，用自己喜欢的细线、铁丝或者铅笔、直尺等用品去围一围，在不同的实践体验中收获不一样的感触，并从中感悟出围成的要义，进而为学生们更科学地理解围成、建构围成概念助力。同时，这样的自主体验、合作分享等系列学习活动，还可以规避教师讲、课件演等活动中的不足，也会使“围”的认识根植于学生脑海之中，像案例中的三角形判定和后续选小棒围三角形等学习活动就会更加顺畅，也会摆脱那份凭感性而论的现象，使数学学习伴随有更多的思考与理性因素。

2. 抓牢“围成”促深入

本节课教学的着力点是：小组合作学习，用三根小棒围一围，并观察发生的数学现象，深入思考現象背后的数学属性。其间，教者如能抓牢“围成”二字，做细操作活动指导，势必会把数学学习引入崭新的天地，也会让学生进一步理解“首尾相连”的要义，真正把握三角形三边关系的内涵。

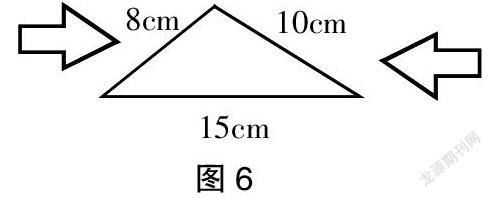
为此，笔者认为，教师的实践操作指导要再细化点。如，针对选用10厘米、8厘米、15厘米的学习小组，教者应在小组实践和演示活动中给予更规范的指导，让学生体会到“围”的基本要领。应组织两次实践，第一次活动过程：一是安排小组成员拿稳15厘米的小棒;二是安排另外两个学生分别拿稳10厘米、8厘米的小棒，并把各自的一个端点交给第一个学生，使其紧紧捏住15厘米的2个端点（每一个端点都与另外一条线段的端点紧紧地贴在一起）;三是指导合作的两个学生轻轻地往内侧压下10厘米和8厘米的小棒，观察这两根小棒的另外两个端点，最终会贴在一起，形成封闭的图形。

第二次活动过程：继续上述活动，加大压力，使8厘米、10厘米的小棒继续往下压，并最终和15厘米的小棒重合。引导学生观察此时的现象。真实的操作，使学生感悟到10+8>15，这样的过程远比组织更多的论述来得更直观、更具体。同时，如果我们用同样的策略引导学生去解读5厘米、10厘米、15厘米与5厘米、8厘米和15厘米这两种情况，那么学生会在具体的情景中体会到不能围成三角形三边之间的内在关系，为揭开三角形三边关系的面纱提供最基本的保障和最科学的感知来源。

操作是学习研究的助手，这点应成为学生实践活动预设的基本准则。从上述案例的思考来看，如果教者能把学生的活动再延伸点，学习研究的深度会增加，所以在教学中我们不能只盯住学生能动起来，要关注知识建构的科学性，也要关注学生的思维动起来。当然，怎样让学生的思维贴近学习、贴近实践操作活络起来，还需要我们做精细的活动谋划与精准的学习引导。

3. 反思操作促务实

2011年版《数学课程标准》明确指出：学生学习应当是一个生动活泼的、主动的和富有个性的过程。除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。从中不难看出，要使学生的数学学习体现个性，体现创造性，达成一种理想的境界，就得让学生的手动起来，口说开来，更要想方设法地使他们的思维活起来，只有这样的状态下，学生的数学学习才是有趣的，才是有热情的。

纵观教学片段，我们能够看到执教者的匠心，也看到学生在活动中的那份自信与智慧。但我们更应关注到的是其间操作的实效性提升问题，如何通过活动的组织和实践操作的感悟与反思，使实践操作活动真正走进知识的深处，真正能成为揭开知识迷雾的有效力量。其中，笔者穿插的点滴思考或许能起到抛砖引玉的作用，或许能成为同行们一丝思考的引子。

总之，教学中组织的学生实践操作活动不是花架子，而是学生学习理解的助推器，一种有效的手段。让操作更務实，不仅要有具体的实践活动，还要有学习活动反思的引导。因为活动是一种媒介，是数学学习的一种凭借，而不是终极任务，所以教学中我们得深入解读文本，把握教材编写意图，并以此来谋划教学活动，引领学生实践操作，让他们在实践中获得感知，形成表象，引发学习思考，从而使数学学习行走在智慧之路上。