丰厚感知 让有效学习有根基

黄杰

[摘  要] 丰富学习感知，是学生们有效学习的基础，也是他们探究知识本质、积淀知识素养的根本所在。为此，教师就得做好激趣引入，诱发观察;实践探究，助力思考;训练反思，加速建构等教学谋划，让学生在有效的情境中积极探索，快乐学习，最终实现数学学习的顺利推进，实现数学核心素养的不断积淀。

[关键词] 感知;有效;学习;丰厚;根基

在小学数学教学中，为引导学生进行最有效的学习观察、学习思考、归纳推理等，教师就得千方百计地创设问题情境、实践操作情境等，并搭建合适的问题探究平台，帮助学生形成有效的学习感知，促使其知识感知积累愈加丰厚，进而助力有效学习生成，促进数学思维、数学素养等不断发展。

在此，笔者截取五年级“简易方程”的教学片段，粗浅地谈谈如何利用必要的探究学习体验，帮助学生积累丰厚的学习感知，以促进他们学习感悟的深入，使得学习、思考等成为一体，也使得他们的数学学习更加睿智、充满活力等。

一、激趣引入，诱发观察

简易方程的学习，对于小学生而言，既是陌生的，也是有基础的。究其知识发展轨迹，我们不难发现“含有未知数的等式”不只是从五年级才开始学习，而是在最初的一年级数学教学中就有大量的体现，比如在括号或方框中填上合适的数等练习，就是最好的例子。所以，在简易方程课堂教学中，教师一方面要激活学生的知识储备和数学学习经验等，另一方面还得通过更为翔实的例子，以丰富学习感知，促进学习思考深入，为他们形成简易方程的概念、建构简易方程的认知等提供知识支持和思维保障。

师：老师给大家带来一年级一组习题，请看看，还熟悉吗？还有什么新的思考和发现？

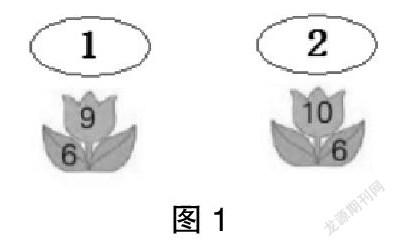
课件呈现学习素材：（1）如图1。

（2）4+□=7，8-□=3等。

生：材料（1）中图1是问9可以分成6和几，10可以分成6和几。

生：材料（2）中的式子一个是要算出加数，另一个是要算出减数。

生：图1中的小花图也可以改写成材料（2）中的那种算式。6+□=9，□+6=10。

生：我发现这些算式都是一个个相等的式子。

生：就是等式，但是也有一个数是不知道的。

师：不错！这样的算式就是等式。你还能写出一些等式吗？

生：2+3=5，s=a×b等。

生：c=a×4，3×7=21等。

生：10×10=100，○÷□=△等。

……

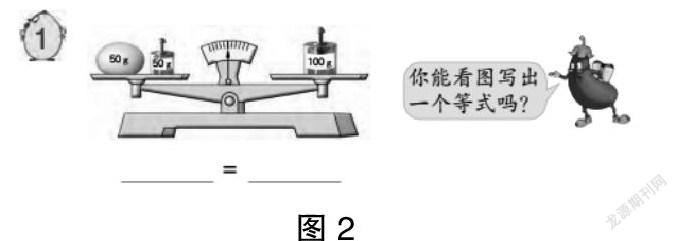
师：这里有一幅图，你能写出对应的算式吗？（课件呈现，见图2）

……

思考：

把脉好学生的知识积累现状，用活这部分知识经验等，引领学生们去观察、分析，既使得简易方程的核心知识点在回忆中留下印象，又能让学生体会到一年级乃至后续的学习中是有大量的等式的，只不过我们没有很好地去观察它、理解它而已。

为此，笔者通过再现一年级的数学内容，引导学生进行有效观察，发现其中的共性知识。同时，引导学生举例，当学生在举出不同的等式时，他們的学习视野得以扩张，学习思考也会随着素材的积累而不断深入。大量的感知冲击，能够让学生在比较感兴趣中快乐学习，促使他们积极地投身于有效的发现学习之中，也使得他们的学习活力得以保持，学习研究充满活力。

二、实践探究，助力思考

引导学生进行有效的实践探究，是他们学好简易方程的有力抓手，也是让他们亲历知识形成活动的基本方式。所以，在简易方程教学中，教师就得引导有效的学习观察，并学会运用知识去解读教材中的所有天平图，从而在思考中发现天平平衡意味着相等的原理，进而建立等式的概念，为进一步提炼方程的意义提供感知力量，为理解和掌握方程的基本原理奠定数学知识基础。

生：刚才的天平图（如图2），我们认为左右相等，就是50+50=100。

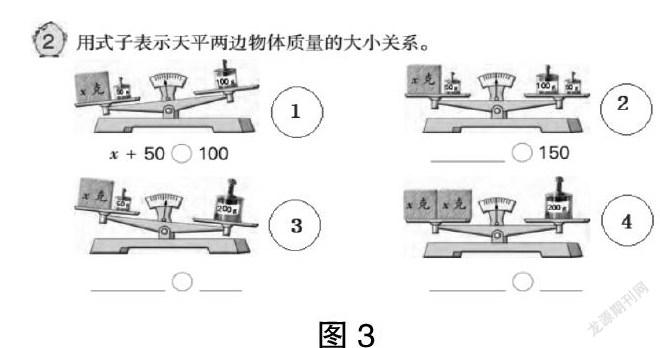
生：例题2中的4幅图（如图3），有2个是相等的。第2个和第4个是相等的，它们的式子是x+50=100+50，x+x=200。

生：是的，但是第1个和第3个是一边翘起来的，说明它们是不相等的。x+50>100，x+50<200。

师：从中不难看出，有的天平是平衡的，写成的算式是相等的，是等式;还有的天平是倾斜的，所以写成的算式就是不相等的，是不等式。你的心中还有怎样的式子是等式呢？

生：山羊+绵羊=羊的总和。

生：（  ）×6=300，60-□=20等。

生：A+B=C，2a=100等。

……

师：我们收集整理了这么多的等式，x+50=100+50，x+x=200，50+50=100，山羊+绵羊=羊的总和，（  ）×6=300，60-□=20，A+B=C，2a=100等。你会对它们进行分类吗？

生：一类是英文字母，一类是数字，一类是文字或符号。

生：我认为一类是关系式，一类是需要计算才能得到结果的等式。

……

师：实际上数学家们把等式进行了这样的分类，一类是有未知数的，也就是刚才同学们议论的需要计算才能得到结果的那种等式，一类是没有未知数的。你能听明白吗？

生：什么是未知数？

生：就是不知道的数字啊！

生：也不全对吧！应该是不知道的，但还能计算出来的，比如（  ）×6=300，60-□=20中的（  ）、□里的数，都是可以算出来的。

生：是的！像A+B=C是难以有一个明显的结论的，像50+50=100就是一个计算等式。

……

师：不错！那上面的式子中哪些是含有未知数的等式呢？

生：经过分析，我们认为x+50=100+50，x+x=200，（  ）×6=300，60-□=20，2a=100，这些都是含有未知数的等式。

……

师：非常正确！我们把这种含有未知数的等式，叫作方程。同伴交流，什么是方程？研究方程要抓住哪些重点要素？

学生小组合作探究，研究讨论方程的意义。

生：方程必须是等式，还要含有未知数。

生：我们认为，未知数可能是x，也可能是（  ）、□，还可能是一个汉字或其他字母。

生：这点很有意义，所以☆×8=200就是方程。

师：正确！每个同学都写出几个方程并与同伴分享，要好好地说明一下理由哦！

学生活动，写方程，说想法等。

……

思考：

方程的本质是等式，是含有未知数的等式。这是孩子们学习的难点，也是理解和掌握方程概念的关键点。为此，笔者在这两个层面都投放了大量的精力，引导学生去观察、比较、分析、归类等，使得感知愈加丰厚，也使得学生有了思考和研究的基础与素材。

教学中首先抓牢教材中的例题，以例题中的情境图为切入口，帮助学生建立等式概念。同时，也让学生在不同的表象冲击下更科学地理解等式的意义，明白等式是算式左右两边相等的式子，从而帮助学生较好地区分不等式。紧接着，引导学生用自己的知识、经验去写一写等式并组织展示交流，从而进一步拓展了他们的学习视野，使得关于的等式的感知表象积累达到了一定的厚度。

其次，引导学生把等式进行分类，以引起学生的争辩，通过质疑等措施，让学生逐步感悟到等式的分类，特别是那些含有未知数的等式，进而使方程的概念得以初步形成。同时，学生们在不同角度的问题引领下，更科学地理解未知数的概念，使得他们对未知数有一个全面、科学的解读，也使得方程的概念理解愈加深刻。

三、训练反思，加速建构

练习的本质就是运用既有的知識、经验与思维等去研究问题、解决问题，并在问题突破中更好地建构认知，有利于学生数学能力的有效发展。为此，在简易方程的教学中，教师就得善于利用教材的编写特点以及学生的学习需要等，科学地设计一系列的问题研究性练习，让学生在训练研究中学习观察、学习分析、学习思考、学习应用知识，从而实现有效学习的打造，促进学生数学素养的积累。

师：学习了这么多的内容，你会运用所学的知识去判断下列的式子谁是等式，谁是方程吗？

（1）6+x=14;（2）36-7=29;（3）60+23>70;（4）8+x;（5）50÷2=25;（6）x+4<14;（7）y-28=35;（8）5y=40。

生：（1）（2）（5）（7）（8）都是等式，因为这些式子中有等于号。

生：是这样的，用等于连接成的式子就是等式。

生：方程只能在等式中寻找，它是（1）（2）（7）（8）。

生：肯定有问题，如果（2）是方程，那么（5）和它是一样的，也应该是方程，但你却没有选，所以肯定是不对的。

生：是的！（2）（5）是等式，但它们没有未知数，所以不是方程。

师：经过辩论，你对方程与等式的关系理解得怎么样？

生：方程一定是等式，但是有的等式却不是方程。

……

师：归纳得很有水平！那下面的问题，你会思考吗？将每个算式中用图形表示的未知数改写成字母。（1）3+▲=10;（2）■×6=48;（3）240÷●=8。

学生自主练习，并通过学习成果汇报引发学习议论。

……

思考：

采取多元化的练习，不仅能更好地巩固知识，深化理解，更有利于调节学生的学习注意力，让他们更愿意参与到多样化的练习之中。教学中，笔者依托教材，没有刻意地设计更多的训练题，而是紧紧围绕教材，用好教材。其间，不只是为了解题而解题，而是把思考、说理有机融合在一起，使得学生对方程的理解更加深刻，也使得等式、方程之间的逻辑关系在学习中逐渐被感悟、被理解。

总之，在简易方程的教学中，教师要精准地把脉学生数学学习的认知规律和知识结构，并以此为源点，引导学生观察、分析、讨论等，以实现感知变得更加丰厚，理解变得更加深入，从而更好地调动学生的学习热情，并在集体思维的交互中实现学习的有效推进，实现简易方程认知的科学建构。