高山嵩草气孔导度对环境因子的响应模拟
2021-01-16李泽卿黄永梅潘莹萍陈慧颖胡广荣杨崇曜
李泽卿,黄永梅,潘莹萍, 陈慧颖, 胡广荣, 杨崇曜
北京师范大学地理科学学部,地表过程与资源生态国家重点实验室, 北京 100875
气孔是土壤-植被-大气连续体(SPAC)中物质、能量交换的主要通道[1],对植物本身的水分、气体交换以及维持陆地表面过程的碳水循环和平衡中发挥着关键作用。气孔导度即气孔张开的程度,它是影响植物光合作用、呼吸作用及蒸腾作用的主要因素[2]。最具代表性的气孔导度模型有两类,即以Jarvis模型为代表的环境因子阶乘经验模型与以Ball建立、Leuning修正的表明气孔导度与净光合速率呈线性关系的半经验模型。除了常依赖于野外、实地调查的经验、半经验模型之外,也有许多基于过程和机理的模型被提出,包括针对外界水力控制、内源激素变化、保卫细胞膨压变化等。气孔导度模型在全球变化生态学中的应用广泛,常作为参数化模型应用在陆地生态系统模型及陆面模式中,例如Jarvis模型被应用在Noah陆面模式中计算气孔与冠层阻抗(使用叶面积指数作为比例因子)参数;Ball气孔导度模型常与Farquhar光合作用模型结合为FvCB模型,广泛应用到大量陆地生态系统模型中, 结合气候模式来预测全球变化对植被和大气之间碳、水循环的影响等[2]。
青藏高原作为全球气候变化敏感区,青藏高原地区植物对环境因子变化的响应也成为研究热点,近20年来,国内学者基于定位观测、样带调查、控制实验、室内培养、模型模拟等多种手段,围绕全球变化背景下的高寒生态系统响应开展了大量工作,取得了重要进展[3]。高寒草甸是青藏高原分布最广、面积最大的草地类型,嵩草属植物常成为高寒草甸的建群种。嵩草属植物对UV-B辐射、增温、土壤干旱的生理生态学响应特征已有了一定的研究与认识[4- 6];与木本植物及温带草本植物相比,相同的是,嵩草属植物的光合速率的主要决定因子同样为光合有效辐射、气孔导度、胞间CO2浓度、蒸腾速率等,限制因子有空气相对湿度、土壤水分等;与其不同的是,温度常成为嵩草属植物光合速率的主要限制因子之一[7]。高山嵩草(Kobresiapygmaea)是青藏高原高寒草甸的主要建群种之一,多生长在海拔3800—4500 m的地带。本文基于野外观测实验数据,应用三类气孔导度模型模拟高山嵩草气孔导度对环境因子的响应特征,同时评估三类气孔导度模型对高山嵩草的模拟精度,为青藏高原生态系统对全球变化响应的模拟研究中气孔导度的应用提供科学依据。
1 材料与方法
1.1 研究区概况
本研究区位于青海湖流域的沙柳河子流域,隶属青海省刚察县三角城种羊场,属高原大陆性气候,年平均气温-0.3℃左右,年平均降水量381 mm左右,蒸发量1454 mm左右,日照时长3285 h[8],日辐射强烈,气温日差较大,观测样地(100°14′5″E,37°14′21″N,海拔3300m)位于高寒草甸,群落盖度约为85%,植物优势种为高山嵩草、弱小火绒草(Leontopodiumpusillum)、羊茅(Festucaovina)等,高山嵩草的分盖度可达74%左右。土壤类型为高山草甸土,实验样地土壤厚度约为2.0 m,0—10 cm土层的土壤黏粒(<2 μm)含量为7.23%,粉粒(2—20 μm)含量为80.85%,沙粒(20 μm—2 mm)含量为9.89%。0—10 cm土层的土壤容重约为0.6 g/cm3。0—10 cm土层的有机碳含量为102.41 g/kg。2018年生长季(7—9月)土壤体积含水量平均为16.88%,在4—27%范围内波动,7月13日—7月26日、8月17日—9月30日,土壤含水量大于15%,7月上中旬和8月上旬土壤含水量低于15%。实验样地基岩多为花岗闪长岩和二长花岗岩。
1.2 野外实验测定方法
2018年7月—9月,天气晴好时,在观测样地随机挑选叶子完整、生长状况良好的高山嵩草植株,利用便携式光合作用测定仪(LI- 6400,LI-COR Inc.,Lincoln,NE,USA)测定植物气体交换过程中光合参数、CO2响应曲线和VPD响应特征。光合参数的测定时间为9:00—18:00,选择长势良好高山嵩草丛株,每次测量重复3次,样品室气体流速为500—600 μmol/s。每组测定的光照强度分别在自然光强和饱和光强2100μmol m-2s-1[7](光源采用LI—6400 LED红蓝光源)下测定。测定结束后将所测叶片剪下测定其叶面积,输入Li- 6400光合作用测定仪中重计算。CO2响应曲线的测量方法:使用配套液化CO2钢瓶控制CO2浓度,具体梯度设置为1800、1600、1400、1200、1000、800、600、400、200、100、50、0 μmol/mol,测定光合有效辐射(PAR)为1800 μmol m-2s-1(光源采用LI- 6400 LED红蓝光源)时高山嵩草叶片的CO2响应曲线,测量叶片在每个CO2浓度下适应3min后测定其光合速率,每次测量重复3次。调节叶室内饱和水汽压差VPD的变化的方式为:调节光合仪通气旋钮,控制进入仪器内的空气含水量[9],取VPD初始值约为0.36 kPa(清晨时VPD数值),等待数据稳定后记录初始的气孔导度Gs,逐渐旋紧按钮,VPD值增加,待VPD值以及各项光合指标稳定后(约5min)再次记录,之后重复上述步骤。在以上测定方法下,对各环境因子与光合参数进行测定。
环境数据中,光合有效辐射(PAR)、饱和水汽压差(VPD)、空气温度(Tair)为LI- 6400直接测得,土壤体积含水量由土壤水分温度电导率测量仪(EM50,Decagon Device,USA)测得,使用环刀法取0—10 cm土样,通过透膜法测得土壤的水分特征曲线,拟合得到土壤水势。
1.3 气孔导度模型
本文选取了Jarvis模型、Leuning模型、Gao模型进行高山嵩草气孔导度模拟。Jarvis模型与Leuning模型分别是气孔导度经验模型、半经验模型的典型代表,应用广泛。Gao模型基于保卫细胞膨压对环境因子的响应机理提出,具有代表性与可行性。
1.3.1Jarvis模型
Jarvis模型是气孔导度Gs的阶乘型经验模型,假设Gs对每一个环境因素的响应是独立的,将Gs表示为多个环境因子函数的乘合,表示这些因子对叶片气孔导度的综合影响,模型具体形式为:
Gs=f(PAR)f(VPD)f(T)f(Ca)
(1)
式中,Gs为气孔导度(mol m-2s-1);f(PAR)、f(VPD)、f(T)、f(Ca)分别为光合有效辐射强度PAR(μmol m-2s-1)、饱和水气压差VPD(kPa)、气温Tair(℃)和大气中CO2浓度Ca(mg/L)对气孔导度的影响函数,其函数值均在0—1[1]。本研究中主要考虑了PAR、Tair和VPD对气孔导度的影响,采用常用的经验公式如下[10]:
(2)
式中,a1,a2,a3,a4,a5,a6,a7均为待定参数。
Jarvis模型在每个环境因子均独立影响气孔导度的假设下,表现出气孔导度与环境因子之间的非线性关系,不同研究者根据自己实验对象和试验地情况的不同,在所应用的Jarvis模型中所考虑的环境变量,以及环境变量的响应函数也有所不同[10-11],因其形式简单灵活,该模型在叶片尺度、冠层尺度、景观尺度以及全球气候模式中均有广泛应用:常被应用于作物叶片气孔导度模拟,如玉米[12-13]、水稻[14]、冬小麦[15]等;在冠层尺度常与蒸腾模型结合来计算冠层导度或蒸腾速率[16-18];Jarvis模型也常被应用在更大尺度的研究中,如Jarvis模型被应用在Noah陆面模式中作为参数化模型利用四个环境胁迫计算植物气孔阻抗,同时也被纳入全球或区域植被-气候模型,用来计算全球空气质量模型中气体沉积(如O3等)的气孔组分等[19-22]。
1.3.2Leuning模型
本研究采用了目前广泛应用的Leuning模型[23]:
(3)
式中,An为净光合速率(μmol m-2s-1);hs为叶表面处空气的相对湿度(%);Cl为叶表面CO2浓度(mg/L);b1、VPD0、g0(理论上为光合速率趋于0时叶片最小气孔导度)为待定参数。Г为CO2补偿点(mmol/mol),利用实测CO2响应曲线计算得到。本研究采用直角双曲线模型来描述高山嵩草净光合速率随CO2浓度的变化规律[1]。
(4)
式中,η为表观羧化效率,即CO2响应曲线的初始斜率;Ci为胞间CO2浓度(μmol/mol);Anmax为CO2饱和时光合速率(μmol m-2s-1),Rp为光呼吸速率(μmol m-2s-1)。计算出方程参数后,令An=0即得到CO2补偿点Г。
在考虑PAR与Tair因子对模型影响时,将式(3)中An使用常用叶片光合速率公式[23]表示:
(5)
式中,α为叶片光合量子效率;Ip为叶片所获光合有效辐射[24-26]:
Amax=Amax(Topt)×f(Tleaf)
(6)
(7)
式中,Amax(Topt),最适温度下某一CO2浓度以及光饱和条件下的最大光合速率,选取实测数据中,饱和光强2100 μmol m-2s-1下,CO2浓度为360 mg/L左右时的数据。式(7)为叶温对Amax的调节函数,T、Tmin、Topt、Tmax为高山嵩草观测汇中的环境温度(Tair)、最低温度、最适温度和最高温度;C为温度修正系数:
(8)
BWB-Leuning模型(BWB,Ball-Woodrow-Berry)是目前应用最为广泛的半经验模型,Leuning模型为针对BWB模型的修正模型,将叶片表面CO2浓度Cs修正为Cs-Г;使用饱和水汽压差VPD替代空气相对湿度。该类模型假设在在叶片表层CO2、空气湿度和土壤水分均处于稳态时,气孔导度与净光合速率之间为线性关系[27]。Leuning模型能够较好描述环境因子影响气孔的基本机理,并且易参数化、对实验样本的数量要求较低,在不同实验条件下均可较为准确地预测气孔导度随环境条件的变化[28]。叶片尺度的应用包括农业与温室作物等[29-30],且BWB-Leuning模型经常与光合模型耦合(如C3植物与Farquhar光合模型[31]、C4植物与Collatz光合模型[20]等)来探究植物光合速率等光合特征与环境因子的关系;冠层尺度的应用中,BWB-Leuning模型常与能量平衡模型及多层模型耦合,上升至冠层尺度后计算森林碳水通量等[32]。全球模式的应用中,BWB-Leuning模型常与气候模式结合来预测全球变化对植被和大气之间碳水循环的影响[33]。
1.3.3Gao模型
本文选取了Gao模型作为基于过程的气孔导度模型的代表,Gao模型是基于气孔保卫细胞结构的力学性质和保卫细胞水分关系建立的机理性气孔导度模型,模型基于以下假设建立:(1)气孔导度与保卫细胞膨压成正比关系;(2)土壤与叶片的水势差驱动水分运输;(3)饱和水汽压差VPD驱动水分蒸散发;(4)光合有效辐射强度引起保卫细胞中离子浓度变化从而影响渗透势[34]。具体公式如下:
(9)
式中,Gs为气孔导度(μmol m-2s-1);Ψs为土壤水势(bar);Ip为光合有效辐射(μmol m-2s-1),gom为最大可能的黑暗条件下的气孔导度,kΨ为保卫细胞结构的弹性屈服系数(mmol m-2s-1kPa-1),kαβ为气孔导度对光合行为的敏感性参数(Dimensionless),kβg为气孔导度对水汽压差的敏感性参数,dvp为大气水汽压相对差(饱和水汽压差VPD与大气压Pa之比)。
在考虑Tair因子对模型影响时,因温度影响VPD,故将VPD表达为[35]:
(10)
式中,RH为相对湿度(%),Tair为气温(℃)。
Gao机理模型比起经验模型与半经验模型更具有机理性,且使用土壤到叶片的水力导度近似表示植物内水分变化引起的保卫细胞的膨压变化,更易计算,可行性更高。因其对于水分条件影响气孔导度的模拟更为准确,因此Gao模型目前常被应用于干旱半干旱地区植物的光合特征、蒸腾作用研究及抗旱性分析等[36-39]。
1.4 数据分析
应用Excel 2010对试验数据进行汇总统计。使用MATLAB R2014a对模型参数进行率定,且进一步进行模拟值与实测值的验证比较,通过决定系数(R2)和均方根误差(Root mean sguare error, RMSE)以及AIC(Akaike information criterion)判定模型模拟效果,使用F检验与P值来检验显著性。
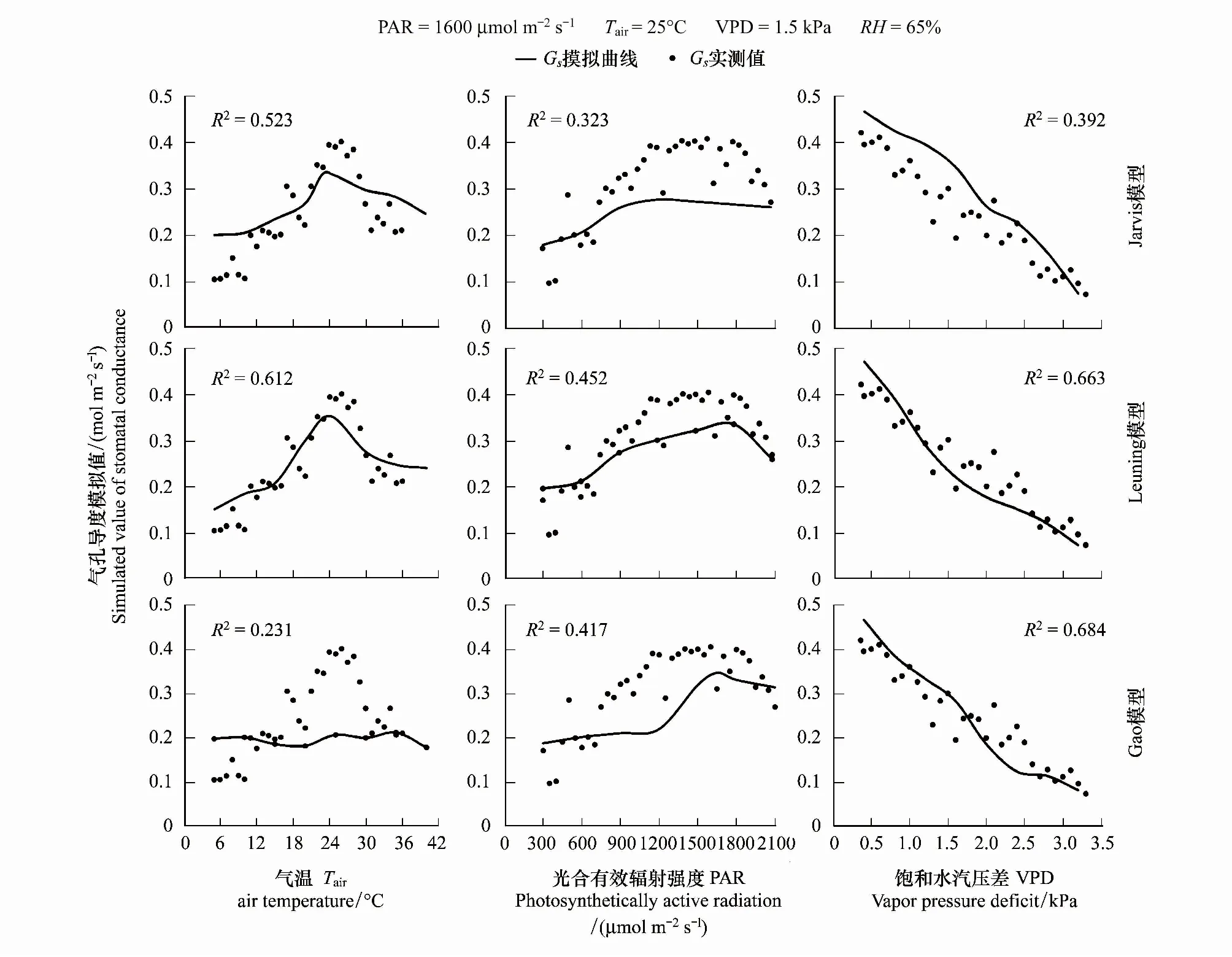
探究三个环境因子逐步发生单位改变时,气孔导度的响应情况,以确定不同环境因子对气孔导度影响程度及各个模型对环境因子的响应是否敏感。对于图4中每个子图,除横坐标表示特定变量逐步发生单位变化,其余环境变量都保持恒定,且等于参考状态(PAR=1600 μmol m-2s-1,Tair=25℃,VPD=1.5 kPa或RH=65%),散点为满足环境变量条件的实测数据。使用加权平均数法得到各环境因子单位变化下气孔导度实测值与三个模型模拟值的相对变化率,以其作为表示响应敏感性的指标:
(11)
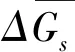
2 结果与分析
2.1 气孔导度模型参数率定和检验
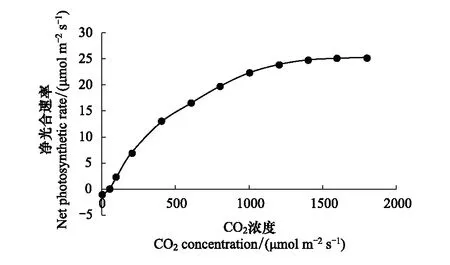
图1 高山嵩草CO2响应曲线Fig.1 CO2 response curve of Kobresia pygmaea每个数据点为多次测量的平均值
直角双曲线模型对高山嵩草CO2响应曲线如图1所示,使用直角双曲线模型对CO2响应曲线进行拟合,参数见表1,令An=0即得到CO2补偿点Γ。
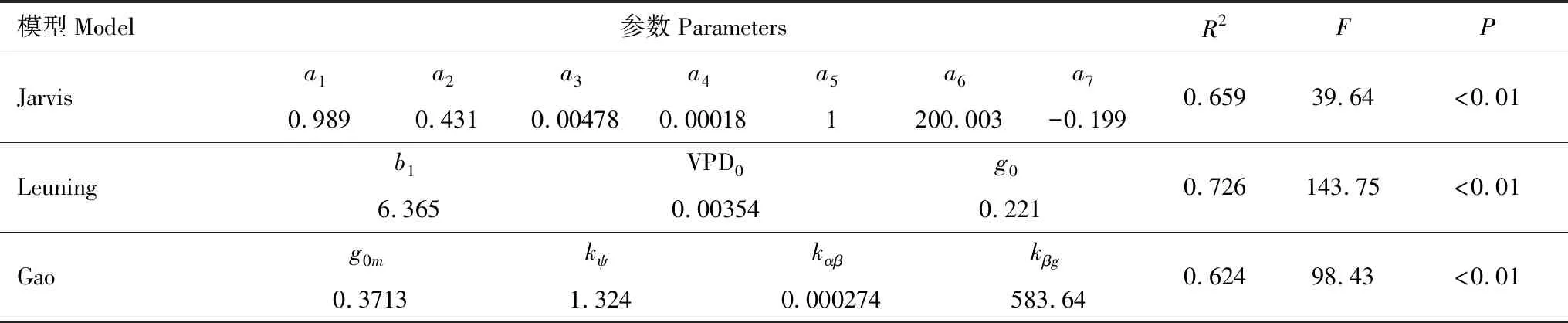
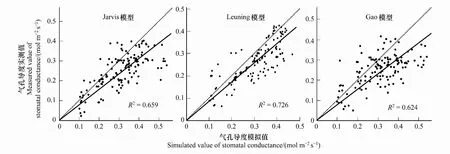
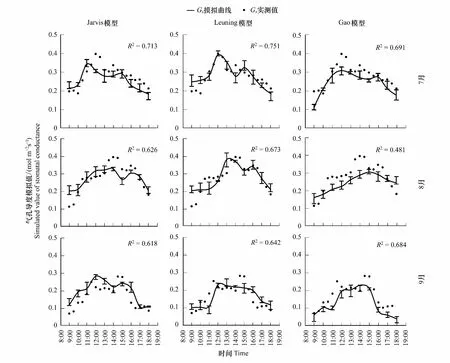
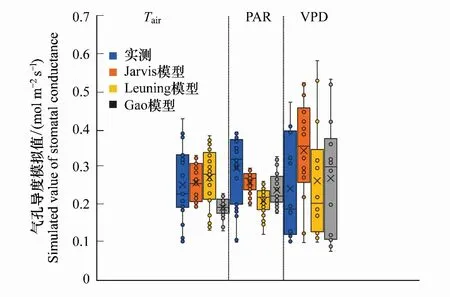
将野外测定数据代入方程(2)—(5)中,可得到方程参数及模拟效果如表2与图2所示。本文选用决定系数R2、均方根误差RMSE以及Akaike信息准则(AIC)来表示模型模拟效果。如图2及表3,将Jarvis模型,Leuning模型和Gao模型的模拟值与实测值的决定系数R2进行比较,Leuning模型> Jarvis 模型>Gao模型;均方根误差(RMSE)则为,Leuning模型< Jarvis 模型 表1 CO2响应曲线-直角双曲线模型参数 表2 气孔导度模型参数 图2 Jarvis气孔导度模型、Leuning气孔导度模型与Gao气孔导度模型的验证比较Fig.2 Validation and comparison of Jarvis model, Leuning model and Gao model 表3 气孔导度模拟值验证效果比较 使用Jarvis经验模型、Leuning半经验模型、Gao机理模型,分别对高山嵩草气孔导度生长季日变化进行模拟。如图3所示,对于观测值,7—9月的每个月日变化曲线基本呈双峰趋势,7月峰值出现在12:00、14:00左右;8月峰值出现在14:00、16:00左右;9月峰值出现在12:00、15:00左右。一天中,午间气孔导度下降幅度为8月最小,7月最大;9月的气孔导度值整体较7、8月有明显降低。基于模拟,高山嵩草瞬时气孔导度最大值出现在8月(0.398mol m-2s-1),最小值出现在9月(0.031 mol m-2s-1),8月极差最大(0.321 mol m-2s-1),日均值依次为7月(0.287 mol m-2s-1)>8月(0.251mol m-2s-1)>9月(0.172 mol m-2s-1)。 图3 2018年7月、8月和9月高山嵩草气孔导度日变化过程模型模拟Fig.3 Simulation of diurnal changes of Kobresia pygmaea′s stomatal conductance in July, August and September 2018 2018年生长季中,使用3个模型模拟高山嵩草生长季(7—9月)气孔导度的日变化过程结果如图3所示。从模拟曲线趋势及峰值来看,Jarvis模型模拟曲线呈现双峰变化,7月峰值出现在11:00、15:00左右,8月峰值出现在14:00、16:00左右,9月峰值出现在12:00、15:00左右。Jarvis模型7、8月峰值均比实测值低;Leuning模型模拟曲线7、8月呈现双峰变化,9月模拟趋势先增大后减小。7月峰值出现在12:00、15:00左右,8月峰值出现在13:30、16:00左右,9月最大值出现在12:00左右。Leuning模型模拟峰值均与实测值相近;Gao模型模拟曲线7月、9月呈现双峰变化,8月为单峰曲线。7月峰值出现在12:00、16:00左右,8月峰值出现在15:00左右,9月峰值出现在12:00、14:30左右。Gao模型模拟峰值均比实测值低。Leuning模型对于3个月份的高山嵩草气孔导度Gs日变化模拟曲线的变化趋势、峰值出现时间均与实际观测值较为接近;Jarvis模型7、8月模拟曲线趋势正确,模拟值总体比实际值偏小;Gao模型的日变化模拟趋势基本正确,但模拟值总体比实际值偏小,8月为单峰曲线,与实测趋势不符,三个月份的峰值出现时间、峰值大小与模拟精度不如Jarvis和Leuning模型,但9月模拟效果在三个模型中最好。从各模型的决定系数R2(图3)可看出,针对7月与8月的气孔导度日变化过程,Jarvis模型模拟效果最好,Jarvis模型优于Gao模型;9月的气孔导度日变化过程,则为Gao模型模拟效果最好,Leuning模型优于Jarvis模型。 图4 高山嵩草气孔导度对主要环境因子的响应模拟Fig.4 Response simulation of Kobresia pygmaea′s stomatal conductance to main environmental factors 在本次实验观测中,在生长季(7—9月)期间,高山嵩草的瞬时气孔导度测定的最高值为0.429 mol m-2s-1,最低值为0.102 mol m-2s-1。假设其他因素对气孔导度Gs的影响不变的情况下,根据观测值及三个模型的模拟值,探究高山嵩草气孔导度对三个环境变量(Tair, PAR, VPD)的响应。如图4所示,高山嵩草气孔导度对3个环境因子的响应特征为:(1)气孔导度Gs在5—35℃气温范围内呈现“钟形”(bell-shaped)响应,在Tair为24.83℃时达到最高值,模型模拟的高山嵩草气孔开放的最适温度,为22.92℃(Jarvis模型)、24.14℃(Leuning模型);(2)气孔导度Gs随着光合有效辐射强度PAR的增加(305—2100μmol m-2s-1)而增加,在高PAR时气孔导度Gs增速缓慢后,出现下降趋势;(3)气孔导度Gs随着饱和水汽压差VPD增加(0.12—3.48 kPa)而降低。将各模型模拟曲线变化趋势与实测数据比较,及模型的决定系数R2(图4)可看出,对于Tair,Leuning模型的模拟效果最好,Jarvis模型次之,模拟也较为准确,Gao模型对Tair因子变化的响应效果较差;对于PAR,Leuning模型的模拟效果最好,Gao模型优于Jarvis模型,在PAR较高阶段,Jarvis模型模拟曲线始终保持较为稳定的状态,较早出现光饱合现象;对于VPD,Gao模型的模拟效果最好,Leuning模型优于Jarvis模型。Gao模型与Leuning模型模拟曲线在VPD为1.5—2.5kPa之间的变化趋势有所不同,Gao模型更接近实测值变化趋势。 图5 三个环境因子(Tair, PAR, VPD)单位变化下实测值与模型模拟值变化特征Fig.5 Change characteristics of measured values and model simulated values under the changes of three environmental factors (Tair, PAR, VPD) 观测值与3个气孔导度模型的模拟值在不同环境因子发生单位变化时的离散分布情况见图5,气孔导度观测值的离散程度为:VPD>PAR>Tair,即VPD的变化对气孔导度的影响较大,数值差异较大。Jarvis模型与Leuning模型模拟值的离散程度为:VPD>Tair>PAR,Gao模型模拟值的离散程度为:VPD>PAR>Tair。从数值分布角度,根据各个盒长及在象限内分布位置,对于VPD与Tair因子,Leuning模型与实测值更为接近;对于PAR因子,三个模型均与实测值有较大不同,Gao模型更为接近。 3个环境因子(Tair、PAR、VPD)逐步变化的影响下,实测值与3个模型模拟值的相对变化率,即敏感度见表4。从表4可知,实测值在3个环境因子的单位变化下的相对变化率:PAR>VPD>Tair,3个模型模拟值对不同环境因子响应下的相对变化率均小于实测值,其中,Jarvis模型与Leuning模型的敏感度:VPD>Tair>PAR,Gao模型模拟值敏感度:VPD>PAR>Tair。对于气温Tair与饱和水汽压差VPD,Leuning模型响应最为敏感,且敏感度与实测值更为接近,对于光合有效辐射强度PAR,Gao模型最为敏感,但与实测值仍有差距。综上,相对变化率作为表征指标可用来表示气孔导度对环境因子的响应敏感度,且可以通过对于实际观测值与3个模型模拟值在环境因子变化下的数据分布情况与气孔导度Gs相对变化率,来进一步比较3个模型模拟的准确性。 表4 三个环境因子(Tair, PAR, VPD)单位变化下实测值与3个模型模拟值相对变化率 在高寒草甸中高山嵩草气孔导度季节变化呈现出明显的单峰趋势,最大值基本出现在7月,最小值出现在生长季尾端的9月,这与宋成刚等对青海海北高寒草甸研究结果类似[40]。本研究发现高山嵩草气孔导度日变化在7月、8月和9月均呈现出明显的双峰趋势。这与高丽楠等[41]对于同属高寒草甸常见植物的窄叶鲜卑花、高山绣线菊、木里苔草和四川嵩草的研究不同:窄叶鲜卑花和木里苔草气孔导度日变化为典型双峰曲线,峰值出现在9:00与15:00,与光合速率日变化表现为相同趋势;高山绣线菊气孔导度第一个峰值出现在11:00,13:00降至最低后在15:00—17:00之间变化不大。而四川嵩草气孔导度日变化呈单峰曲线,峰值出现在11:00左右。 本研究中高山嵩草气孔导度Gs在7月、8月和9月的12:00—14:00时间段内,均出现了降低,说明高山嵩草在正午附近,存在“光抑制”现象,关闭气孔,降低气孔导度,减少蒸腾耗水[42]。本研究中高山嵩草气孔导度对光合有效辐射PAR的响应也表现出,当PAR大于1800 μmol m-2s-1时,气孔导度呈明显下降的趋势(图4)。青藏高原地区太阳光照强烈,中午尤甚,光强可达到2000 μmol m-2s-1以上,远比一般植物光合作用饱和光强高,因此高寒草甸植物的光合作用及与其有关的生理生态活动经常遭受“光抑制”现象[43],曾有学者对海北高寒草甸植物的光合作用光抑制问题进行研究,作为光抑制发生的最初部位,光系统I的光化学效率(Fv/Fm)往往被用作判断光抑制发生的指标[43],研究发现,海北牧草的Fv/Fm在中午明显比早晨低,且降低幅度随着日光照射的时间延长而不断增加,由此学者认为高寒草甸植物叶片经常发生光合作用光抑制[43]。与本研究相同的是,在针对青藏高原东缘,四川省西北部的窄叶鲜卑花、高山绣线菊、木里苔草,以及青藏高原东北部的麻花艽(Gentianastraminea)、美丽风毛菊(Saussureasuperba)[44]和矮嵩草(Kobresiahumilis)[45]的研究中,上述植物均出现光合“午休”的光抑制现象,与本研究不同的是,青藏高原东缘的四川嵩草以及青海海北地区高寒草甸的垂穗披碱草(Elymusnutans)[46]均无光抑制现象。在探究植物发生光抑制的原因时,一方面,有学者发现,在强光照射后,随着Fv/Fm逐渐降低,观测到叶片初始荧光显著增加,且观测荧光时叶片已经暗适应半小时以上,说明强光可能已对叶片的光合机构造成破坏[43]。而另一方面,也有不少学者认为,自然条件下的光抑制是植物光合机构为避免光破坏而采取的光合作用下调(Down regulation of photosynthesis capacity)的措施,不涉及蛋白的破坏[44]。另外也有研究者提出,正午时高光强可能通过影响空气温度和叶细胞间隙与冠层间的饱和水汽压差VPD间接引起光抑制现象以及气孔导度下降等相关生理活动[18]。同时,叶片形态也被认为与“光抑制”有一定关系[47],如四川嵩草叶片较厚,叶面积较小,应对强光环境有更好适应性[48],故比起其他高寒草甸植物,没有出现光抑制现象。 本研究中高山嵩草气孔导度Gs对气温呈现“钟形”(bell-shaped)响应,气孔导度观测值随着气温升高,峰值出现在24.83℃,后在高温区段降低;Jarvis模型与Leuning模型气孔导度模拟值达到最大的最适温度分别为22.92℃(Jarvis模型)、24.14℃(Leuning模型)。植物光合作用与气体交换活动关系密切,本研究所得上述最适温度也处于高山植物净光合作用的最适温度范围内(15—25℃)[49]。温度对植物叶片气孔导度的影响,是通过影响植物光合能力达到的,随温度增加,植物表观初始量子效率增加,光补偿点减小,植物吸收与转换光能的色素蛋白复合体较多,光抑制减少,气体交换能力越强,气孔开闭不受限制,气孔导度增大[5]。也有许多学者认为,温度因子与其他环境因子共同影响气孔导度。如温度升高会导致VPD升高,造成气孔导度减小[50];温度变化也会影响植物茎流,使得水势梯度发生变化,影响气孔开闭[51]等。与本研究结果类似的是,师生波等[44]针对青藏高原东北隅高寒草甸主要伴生种麻花艽(Gentianastraminea)和美丽风毛菊(Saussureasuperba)研究发现,随着温度逐步升高并稳定到一定水平,麻花艽与美丽风毛菊的气孔导度均表现为先升高后降低的趋势。王一峰和李怡颖[52]针对青藏高原东北部沙生风毛菊(SaussureaArenariaMaxim)研究发现,在5—30℃范围中,随着温度上升,沙生风毛菊叶片的气孔导度显著上升后下降。郭亚奇等针对藏北高寒草地建群种紫花针茅(Stipapurpurea)的研究发现,气孔导度对不同温度的响应不同,在不同温度下的气孔导度数值大小表现为20℃>15℃>25℃,且温度的升高会导致气孔导度Gs对于CO2浓度变化的响应更为敏感(通过气孔导度的变化率体现)[53]。 本研究中高山嵩草气孔导度Gs随着VPD增加而降低,Gs与VPD呈负相关。植物叶片气孔导度对VPD增加的响应涉及到叶肉细胞或者保卫细胞自身中的水分状态,且有可能由脱落酸(ABA)等激素信号介导,而叶水势和导水率则决定了细胞表皮水势和保卫细胞膨压对VPD变化的响应,具体而言,VPD升高导致水分蒸散增强,引起并加剧了植物叶细胞及茎干中的水势下降,气孔关闭,气孔导度减小;同时VPD驱动的环境中水分的蒸发作用增强,导致的土壤水分流失会使得干旱胁迫更为剧烈,从而加剧气孔导度的减小。同时需要注意的是,VPD升高期间的气孔导度降低会引起光合作用的降低,影响植物的碳水化合物合成与植物生长,时间过长则会引起植物“碳饥饿”[54]。相关研究中,气孔导度对于上升的VPD的响应机制,在不同的气孔导度模型中往往均采用气孔导度Gs随着VPD增加而单调下降的方程形式[54-56],且均在VPD较低时出现气孔导度Gs最大值[54]。在针对其他高寒植物的研究中,也有相似结果,如师生波等[44]研究发现,高寒矮嵩草草甸植物群落环境的VPD逐步升高时,麻花艽和美丽风毛菊叶片气孔导度降低并较长时间处于低水平。在针对木里苔草、四川嵩草和垂穗披碱草的研究中,在VPD上升阶段时,3个物种的气孔导度均出现下降趋势,且气孔导度日均值为木里苔草(沼泽湿地)>四川嵩草(湿草甸)>垂穗披碱草(干草甸)[57]。与此同时,许多相关研究表明,不同生境、不同物种的气孔导度Gs对VPD的响应有不同模式。一般认为叶片气孔导度Gs普遍随着VPD增加而逐渐下降,如作物(如冬小麦[58]、菊芋(Helianthustuberosus)[59]等)、乔木(如梭梭(Haloxylonammodendron)[60]、灰胡杨[61]等)研究结果均与本文类似。然而在针对其他生境生长植物的研究中有着与本文不同的结果,例如,针对干旱半干旱地区的油蒿[62]、白蜡树(FraxinuschinensisRoxb.),新疆杨(PopulusalbaL. var.pyramidalisBge.)以及毛白杨(PopulustomentosaCarr.)[63]的研究,以及热带亚热带地区稀树草原的优势木本植物(该地区草本植物的气孔导度Gs随着VPD增加而降低)[64]、天然马尾松(PinusmassonianaLamb.)和外来湿地松(PinuselliottiiEngelm.)[65]的研究发现,以上植物物种的叶片气孔导度Gs先随着VPD增加达到峰值后,又随VPD增加而减少。上述研究与本文结果不同的原因,在于气孔反应取决于生长条件,植物长期生长在低VPD环境中(即水分条件较好的环境中),叶片气孔对关闭刺激(如ABA等)的反应会不够敏感[66-67],而在高VPD(即水分胁迫较大时)情况下气孔关闭,则是气孔对高VPD引起的叶片保卫细胞膨压变化的被动水力响应[68-69]。有学者也指出,生态系统水平的不等水性(Anisohydricity)用于表示植物在干旱条件下调节气孔和植物含水量的能力[69-71],青藏高原高寒草甸的不等水性较高[72],高不等水性的生态系统通常对VPD变化更敏感[69-71,73]。有学者指出,高VPD引起的气孔导度降低[72-74],光合作用降低,进而会使得高寒草甸NEE(生态系统CO2净交换量)、高寒草甸生产力也随VPD升高而降低[75-76]。 本研究对高山嵩草气孔导度Gs进行模拟和检验,从图2及表3结果,根据决定系数(R2)、均方根误差(RMSE)以及赤池信息量准则(AIC)判定模型模拟效果,三个气孔导度模型均可以较好地模拟高山嵩草的气孔导度,其中Leuning模型最好,Jarvis 模型次之,Gao模型较差。但3个模型对主要环境因子的敏感性不同:Leuning模型对温度因子的响应模拟效果最好,Jarvis模型也有较好的响应效果,Gao模型模拟结果最差。这是因为Leuning模型中气孔导度的模拟耦合了净光合速率的模拟过程,而净光合速率的模拟考虑了温度三基点的影响(见式7)[26],Jarvis模型中用多项式拟合了温度对气孔导度的影响,没有机理意义[56,77],而Gao是基于气孔导度与土壤水势关系提出的,更适用应用于各种水分条件下的模拟[34],模型受温度影响较小,温度因子只能通过影响VPD来影响气孔导度Gs。对于饱和水汽压差VPD的响应,三个模型模拟曲线趋势均良好, Gao模型的响应效果最好,Leuning模型优于Jarvis模型,且前两者在1.5—2.5kPa期间模拟值下降速率有较明显差异。对于光照辐射强度PAR的响应,Leuning模型模拟效果最好,Gao机理模型优于Jarvis模型。因为高寒草甸植被生长主要受温度调控,而与土壤水分关系较小[78],所以对高山嵩草的气孔导度模拟Leuning模型的精度和敏感性都最好。 与前人研究方法不同[62-63],本文对于模型对环境因子的响应敏感性,提出一种新的表示方法,即使用不同环境因子变化下的气孔导度相对变化率来表示,更为直观。根据表4,Leuning模型对气温Tair变化的敏感度高于Jarvis模型,Gao模型对于温度因子的敏感度较差。Leuning模型对VPD变化的敏感度最高,Gao模型比Jarvis模型好。与本研究结果类似的是,王海珍等[61]研究发现,Leuning模型对于灰胡杨叶片气孔导度受水分条件影响较大的时段拟合效果好于Jarvis模型,即Leuning模型对于水分条件的响应更好。Gao模型对PAR的敏感度最高,且Leuning模型敏感度高于Jarvis模型,该结果可对应图4中,Leuning模型与Gao模型在后期PAR较高阶段,气孔导度Gs模拟值均出现下降,而Jarvis模型模拟曲线则较早出现稳定“平台期”。这是因为,Gao模型中,光合有效辐射PAR作为直接输入参数,且比起Jarvis假设各个因子独立作用于植物气孔,Gao模型中kαβ参数可直接反映气孔导度对光合有效辐射的敏感性,与保卫细胞渗透压及弹性模量有关[34];Leuning模型中PAR因子与Amax(其中含有温度修正函数)结合,Gao模型与Leuning模型都考虑了各因子之间的相互作用,故模拟效果更好。 由于野外自然条件下,各种环境因子之间互相影响,因而对气孔导度影响存在交互作用,故气孔对环境因子响应机制复杂。试图模拟或研究高山嵩草叶片气孔导度对单个环境因子的响应规律,无法消除其群落和环境因子相互作用的复杂性所带来的影响。在进一步的研究工作中,可基于高山嵩草气孔导度对不同环境因子响应特点,对模型进行机理性探索与改进,以得到更适用青藏高原地区高寒草甸建群种高山嵩草的气孔导度模型,为青藏高原地区植物叶片、群落、生态系统、景观尺度以及未来全球尺度的碳水耦合过程和气候模型提供参考。 国际上常用的Jarvis模型、Leuning模型及机理模型Gao模型均可以较好地模拟高山嵩草气孔导度对环境因子的响应特征。总体来说, Leuning模型准确度最高,Jarvis模型次之,Gao模型准确度最低。高山嵩草气孔导度对各环境因子的敏感性排序为:PAR>VPD>Tair;3个模型中,Leuning模型对光合有效辐射强度PAR和气温Tair最敏感,模拟准确度最高;Gao模型对饱和水汽压差VPD最敏感。高山嵩草气孔开放的最适温度,分别为24.83℃(实测值)、22.92℃(Jarvis模型)、24.14℃(Leuning模型),总体处于22—25℃范围内,可为高山嵩草光合作用及气体交换的三基温中的最适温度提供参考。

2.2 高山嵩草气孔导度日变化模拟
2.3 高山嵩草气孔导度对不同环境因子的响应模拟

3 讨论
3.1 高山嵩草气孔导度对环境因子的响应特征
3.2 气孔导度模型对高山嵩草气孔导度模拟的可行性
4 结论
