一种快速自旋回波的受激回波伪影校正方法
2021-01-15王艳飞覃文军杨金柱
王艳飞, 覃文军, 杨金柱,3, 康 雁,4
(1.东北大学 医学与生物信息工程学院, 辽宁 沈阳 110169; 2.东北大学 计算机科学与工程学院, 辽宁 沈阳 110169;3.东北大学 医学影像智能计算教育部重点实验室, 辽宁 沈阳 110169; 4.深圳技术大学 健康与环境工程学院, 广东 深圳 518118)
快速自旋回波(fast spin echo,FSE)[1],在90°射频脉冲激励后,通过连续施加多个180°回聚脉冲,重聚散相的横向磁化矢量.每个180°回聚脉冲配合不同的相位编码梯度,这样在一次重复时间可以完成多个回波数据采集,提高了成像速度.目前FSE已经成为最常用的临床诊断脉冲序列之一,广泛用于各种解剖部位的磁共振成像中[2-4].
快速自旋回波在一次重复时间通过施加多个180°回聚脉冲来降低成像时间,但由于射频场不均匀、射频功率校正不准确等因素的影响,180°回聚脉冲的翻转角并不能达到理想的180°,导致接收到的回波信号不但包含了自旋回波,还包含了受激回波[5-7].在编码梯度的作用下,受激回波和自旋回波的空间编码信息不一致,最终导致图像产生伪影.
常用的受激回波伪影校正方法包括:①使用粉碎梯度(crusher gradients)[8-10];②通过预扫描进行校正.粉碎梯度方法,通常修改180°回聚脉冲所对应的选层梯度,在选层梯度的两侧各加一个极性相同的梯度,通过这两个梯度对横向磁化矢量进行散相和聚相,改变受激回波的相位,抑制受激回波的产生.粉碎梯度方法并不能完全消除受激回波对快速自旋回波成像的影响.预扫描方法,是在脉冲序列正式扫描前,通过采集额外的校正数据分解出受激回波,并对受激回波进行抑制.一种预扫描方法是通过修改快速自旋回波脉冲序列,在每一个读梯度的两侧分别加上一个散相梯度,校正由受激回波引起的相位差[11];另一种预扫描方法[12-13],通过多次改变粉碎梯度的强度值以及90°射频脉冲和180°回聚脉冲的相位角,使受激回波或者自旋回波消失,实现对受激回波的单独调节.
本文提出一种基于预扫描法的受激回波伪影校正方法,该方法简单、快速,且不需要更改脉冲序列.校正数据采集过程中,只需要更改一次180°回聚脉冲的相位角,就可以分离出受激回波和自旋回波.根据分离出来的受激回波和自旋回波的回波中心位置差,校正读梯度方向的预散相梯度的面积,根据受激回波和自旋回波的相位差修正180°回聚脉冲的相位角,即可完成受激回波伪影校正.
1 算法与模型
1.1 受激回波形成与特点
当180°回聚脉冲的翻转角不是理想180°时,回聚脉冲含有90°射频脉冲的等效分量.受激回波可以普遍表示成由3个连续的90°射频脉冲形成[14-15].为了理解受激回波的复杂形成原理,又不失一般性,本文把横向磁化矢量抽象成6个分量,其中a1,a2,a3逆时针散相,b1,b2,b3顺时针散相.经过时间τ,磁化矢量a1,a2,a3,b1,b2,b3的散相角度分别为θ1,θ2,θ3,Φ1,Φ2,Φ3.其中θ1,Φ1(0,/2),θ2,Φ2=/2,θ3,Φ3(/2,).射频脉冲的持续时间非常短,可以认为瞬时完成.
如图1所示,设z轴与主磁场方向平行,x′,y′轴是与z轴垂直的逻辑坐标系,所施加的3个90°射频脉冲的相位角全为0°.图1a为t=0时刻沿x′轴方向施加第一个90°射频脉冲,纵向磁化矢量翻转90°落在+y′轴上,形成横向磁化矢量.受主磁场不均匀及T2弛豫物理特性影响,横向磁化矢量开始散相,经过时间τ后,磁化矢量散相如图1b所示.
在t=τ时刻,沿x′轴方向施加第二个90°射频脉冲.受射频脉冲激发,所有横向磁化矢量翻转到x′z平面,如图1c所示.其中,a1和b1位于-z平面,a2和b2位于x′轴,a3和b3位于+z平面.此后,所有磁化矢量在x′y′平面方向,继续以恒定的速度绕z轴散相,在t=2τ时刻,所有的磁化矢量的水平分量全部转到-y′平面,产生自旋回波(也称为哈恩回波).
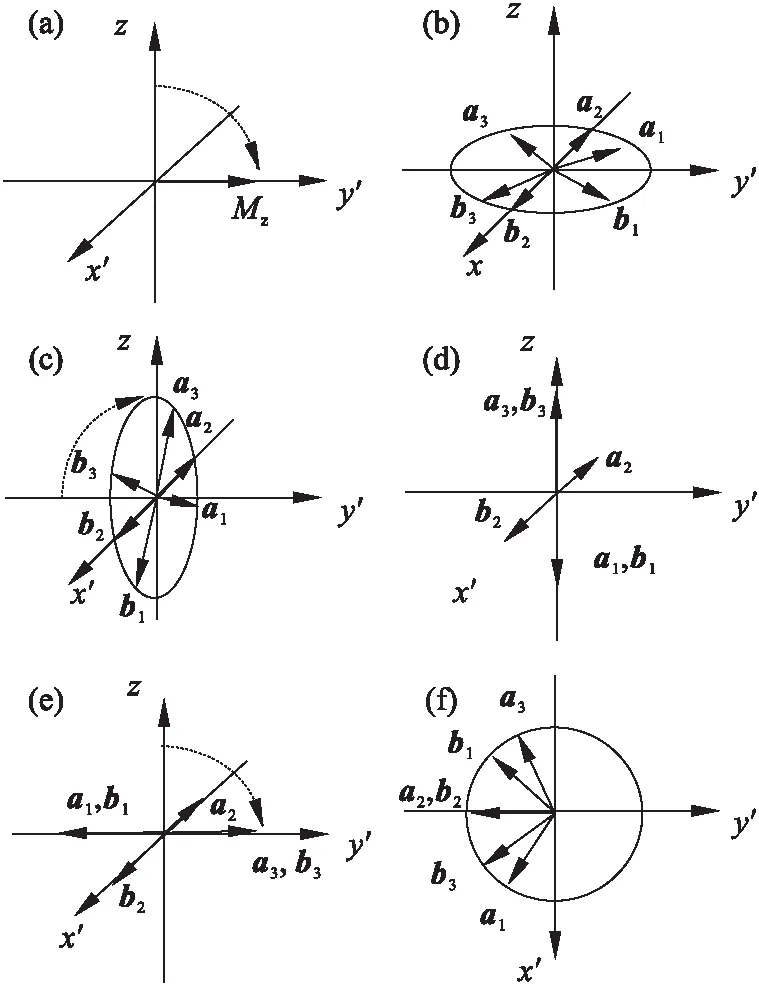
图1 射频脉冲相位角为0°,受激回波形成原理图
在第二个90°射频脉冲施加完成后,仅考虑图1c中磁化矢量在纵向平面的变化情况.此时a2和b2位于x′轴,没有纵向分量,a3和b3的纵向分量位于+z轴,a1和b1的纵向分量位于-z轴,如图1d所示.此后,所有纵向磁化矢量以T1弛豫时间沿z轴方向恢复,磁化矢量在纵向的大小发生变化,但方向并没有变化.
如图1e所示,在t=τ+T时刻,沿x′轴方向施加第三个90°射频脉冲.其中,T为混合时间.此时a3和b3的纵向分量翻转到+y′轴,a1和b1的纵向分量翻转到-y′轴.a2和b2不受射频脉冲的影响,方向不发生变化.此后,所有磁化矢量继续以恒定的速度在x′y′平面绕z轴散相.如图1f所示,经过τ时间后,a1逆时针转θ1角位于第三象限,b3顺时针旋转Φ3角位于第三象限,a2和b2重合位于-y′轴,b1和a3旋转到第二象限.此时,所有横向磁化矢量全部位于-y′平面,在-y′轴产生净磁化矢量,形成受激回波.
上述分析中所有的90°射频脉冲相位角全等于0°,接下来的分析,改变第二个和第三个90°射频脉冲的相位角为90°.如图2a所示,在t=0时刻施加第一个翻转角等于90°、相位角等于0°的射频脉冲.如图2b所示,在t=τ时刻,散相的横向磁化矢量受第二个90°射频脉冲作用,由于第二个射频脉冲相位角等于90°,这时横向磁化矢量会绕y′轴旋转,全部横向磁化矢量都在y′z平面,见图2c.此时,仅考虑磁化矢量在纵向的变化情况,从y′轴观察,a1,a2,a3位于-z轴,b1,b2,b3位于+z轴,如图2d所示.此后,纵向磁化矢量沿z向以T1弛豫时间恢复.在t=τ+T时刻,施加相位角、翻转角均为90°的第三个射频脉冲,见图2e.之后各横向磁化矢量以恒定的速度绕z轴旋转,经过τ时间后所有的纵向磁化矢量全部位于-y′轴,形成受激回波,见图2f.
由此可以得出:①连续3个翻转角为90°的射频脉冲会产生受激回波.实际上,只要射频脉冲的翻转角不等于180°,就会有90°翻转角等效分量,就会形成受激回波;② 3个射频脉冲的相位角分别等于0°产生的受激回波,与3个相位角分别等于0°,90°,90°的射频脉冲产生的受激回波方向相反.
1.2 受激回波校正原理
基于前文分析的受激回波形成原理及射频脉冲相位角对受激回波的影响,本文设计的受激回波和自旋回波分离算法如图3所示.图3a为施加相位角等于0°、翻转角等于90°的射频脉冲对被成像物体进行激发,其中tet代表回波时间.在tet/2 时间施加翻转角等于180°、相位角等于0°的回聚射频脉冲,在3tet/2时间再一次施加翻转角等于180°、相位角等于0°的回聚射频脉冲,在2tet时间采集信号,这时采集到的信号S1既包含自旋回波信号SSE1,又包含受激回波信号SSTE1,可表示为
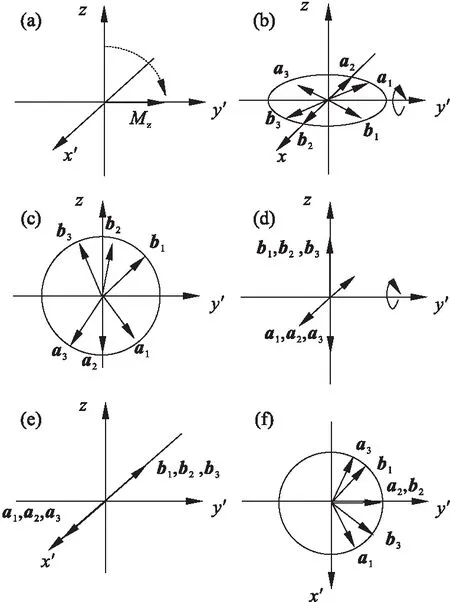
图2 第二和第三个射频脉冲相位角为90°,受激回波形成原理图
S1=SSE1+SSTE1.
(1)
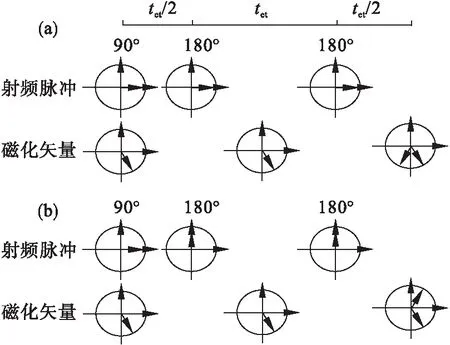
图3 自旋回波、受激回波分离原理图
图3b为施加翻转角等于90°、相位角等于0°的射频脉冲对被成像物体进行激发,之后的180°回聚脉冲相位角均为90°,这时采集到的信号同样包含自旋回波信号SSE2和受激回波信号SSTE2,可表示为
S2=SSE2+SSTE2.
(2)
由于两次预扫描施加的射频脉冲翻转角没有变化,因此SSE1等于SSE2.由1.1节结果可知,两次预扫描采集到的受激回波方向相反,但信号强度相同,因此式(1)和式(2)可表示为
(3)
从式(3)中可以求出自旋回波信号和受激回波信号:
(4)
根据分离得到的自旋回波和受激回波,计算二者的回波中心位置差,补偿读梯度方向预散相梯度A的面积,使自旋回波和受激回波的回波中心重合.预散相梯度A的修正值为
(5)
其中:Cdif为自旋回波与受激回波的回波中心差;s为采样步长;t1,t2分别为预散相梯度和读梯度的持续时间.
由于回聚脉冲的翻转角不能达到理想180°,使自旋回波的相位角φSE和受激回波的相位角φSTE不一致,因此造成图像伪影.对180°回聚脉冲的相位修正为
(6)
2 实验方法
2.1 脉冲序列及参数
采用本文所提出的方法,在1.5 T超导磁共振成像系统对水模进行了实验.实验采用8通道头部接收线圈,水模分别采用硫酸铜分辨率模体和圆柱状模体,对采集到的数据使用交互式数据语言IDL进行数据分析.
FSE脉冲序列的时序如图4所示,Gx,Gy和Gz分别为读梯度、相位编码梯度和选层梯度,Tx/Rx为射频发射和信号接收,ACQ为采集窗.脉冲序列的扫描参数:重复时间为3 600 ms,回波时间为105 ms,扫描矩阵为256×256,回波链长度为16.
2.2 数据分析
为了定量分析受激回波伪影校正对快速自旋回波图像的伪影及信噪比影响,本文以国家食品药品监督管理局发布的“YY/T 0482—2010医用成像磁共振设备主要图像质量参数的测定”为依据,采用如下方法进行定量分析.
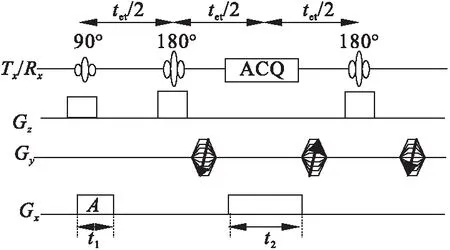
图4 快速自旋回波脉冲序列时序图
对于伪影,计算伪影与信号的比值.采用3个测量值:①在伪影处画感兴趣区域(region of interest,ROI),找到最大伪影值Gmax;②在测量模体内画ROI,计算信号平均值Savg;③在背景处画ROI,计算背景噪声平均值Navg,伪影与信号的比值g为
g=(Gmax-Navg)/Savg.
(7)
对于信噪比,测量方法描述如下:①在背景噪声处画ROI,计算背景噪声标准方差NSD;②在测量模体内画ROI,计算信号平均值Savg.信噪比的计算公式为
RSN=Savg/NSD.
(8)
3 实验结果与分析
图5为分辨率水模的成像结果.经过调整窗宽和窗位后,从图中可以看出,没有经过受激回波伪影校正的图像(图5a),水模内部的结构沿相位编码方向向外有延伸,叠加到水模图像上,形成了伪影(箭头所示位置).而校正后的图像(图5b),受激回波伪影已经得到了抑制.

图5 FSE水模图像
为了定量分析本文所提出的方法对图像的影响,对圆柱状水模进行了成像,并在图像上画了3个ROI,如图6所示.其中ROI 1用于标记水模图像的统计信息,ROI 2用于标记背景噪声的统计信息,ROI 3用于标记伪影的统计信息,ROI的统计值见表1.

图6 快速自旋回波图像伪影及信噪比测量
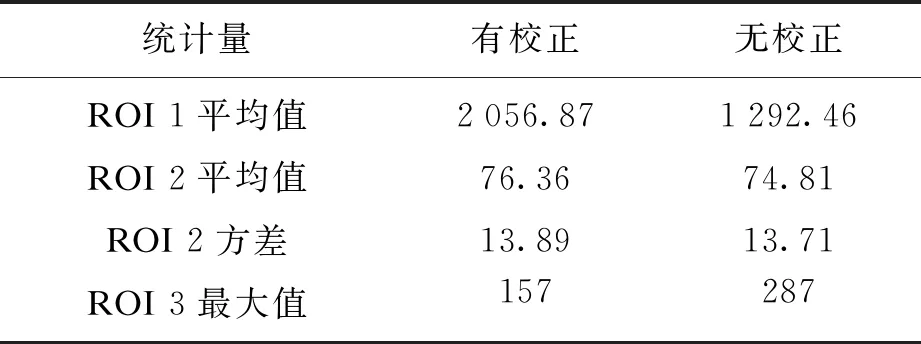
表1 ROI统计信息
伪影和信噪比的计算结果见表2.从表2可以看出,经过受激回波伪影校正后,快速自旋回波图像的信噪比约提高了57.08%,而伪影约降低了76.12%.
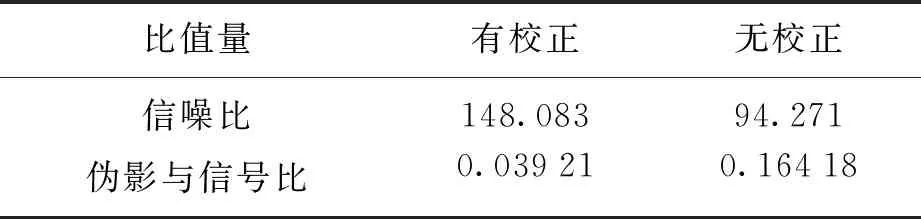
表2 受激回波伪影校正前后的伪影和信噪比定量对比
如图7所示,FSE脉冲序列共激发5个成像层面,图中显示了每一个层面校正前、后自旋回波与受激回波的回波中心与相位的变化情况.从图7a可以看出,校正前每一个层面的回波中心位置与相位均有较大差别,而经过校正后,图7b中所有层面的回波中心位置与相位基本一致.
由于回聚脉冲的翻转角不是理想的180°,受激回波和自旋回波的相位不一致,接收到的信号是二者的合成信号,所以会造成图像信号降低.而经过校正后,受激回波和自旋回波的相位基本一致,接收到的信号不仅有自旋回波信号,还在相同的相位方向增加了受激回波信号,信号强度增大,所以图像的信噪比得到了提高.
从第二个180°回聚脉冲开始,根据回波链的长度,每次回聚,散相的磁化矢量都会产生受激回波,受激回波被施加的空间编码梯度所编码,采样到k空间,扰乱了k空间的编码轨迹.在通过傅里叶变换进行图像重建时,把像素在图像域映射到了错误的位置,因此形成伪影.由于形成过程复杂,受激回波伪影很难通过图像后处理进行校正.
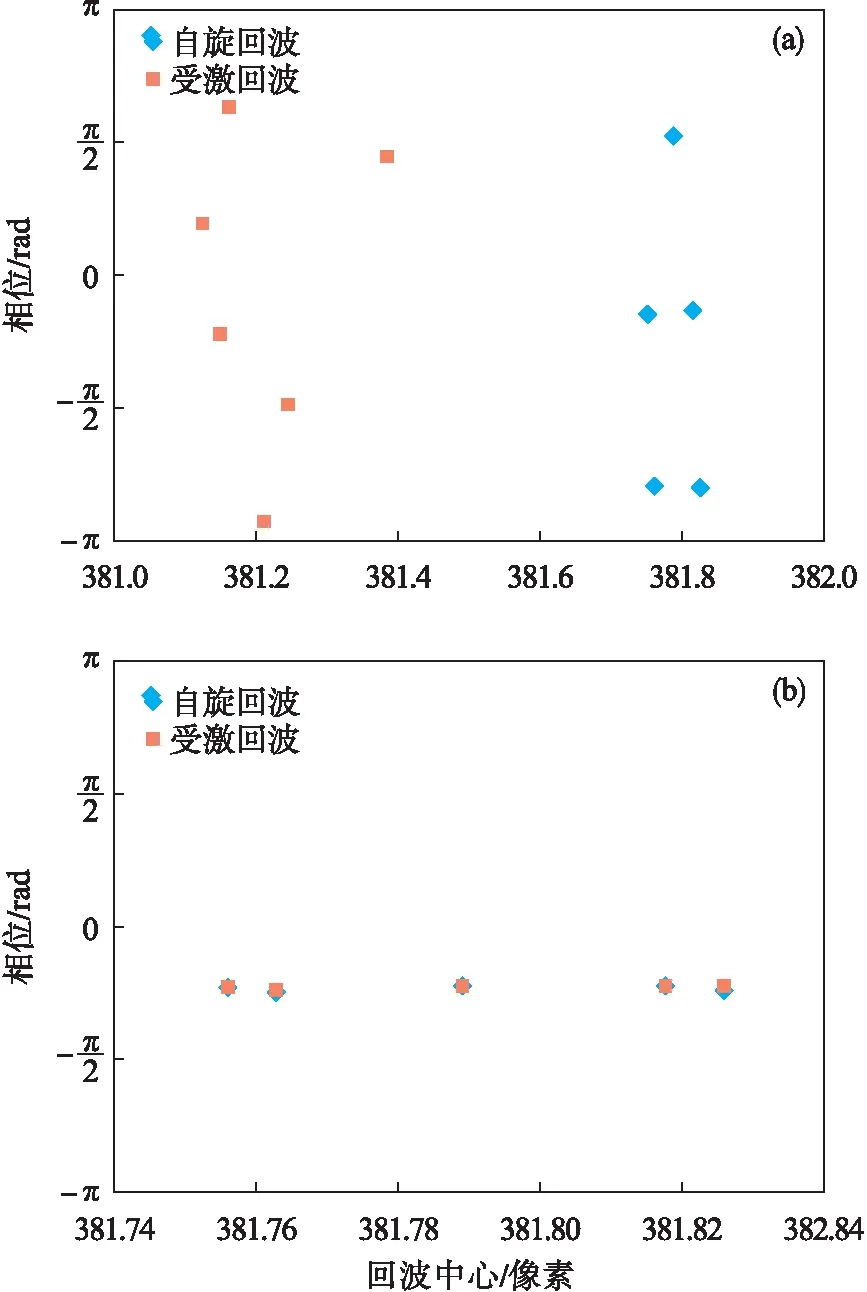
图7 校正前后相位与回波中心变化情况
4 结 论
1) 本文根据受激回波的形成过程,分析出了射频脉冲的相位角对磁化矢量的影响,并以此为依据,分解出受激回波和自旋回波.
2) 通过校正读梯度方向的预散相梯度面积和180°回聚脉冲的相位角,可以实现受激回波伪影校正.
3) 从快速自旋回波的模体图像可以看出,本文提出的方法能有效降低图像伪影,提高图像信噪比.
