考虑铁损的永磁同步电机无位置传感器控制算法

曾小华， 陈虹旭， 崔 臣， 宋大凤

(吉林大学 汽车仿真与控制国家重点实验室， 吉林 长春 130025)

面对日益严峻的能源危机和环境问题，汽车行业正经历着从传统内燃机汽车向新能源汽车的转变，永磁同步电机(permanent magnet synchronous motor，PMSM)因其效率高、调速范围宽等优点，广泛应用于车用驱动电机领域[1].为实现对永磁同步电机的精确控制，常在电机中安装高精度位置传感器，如霍尔传感器、光电编码器等，但是位置传感器的使用会提高电机系统成本，还易受振动、噪声等因素影响降低系统的可靠性[2].因此，在电机控制系统的软件层面开发无位置传感器算法可以有效地降低成本、提高系统可靠性.

无位置传感器算法可分为两类：高频注入法和观测器法.高频注入法主要适用于零速和低速工况，通过外加高频激励实现对转子位置的估计，该方法需设计多个滤波器，控制复杂且运算量大[3-4].

滑模观测器(sliding mode obsever，SMO)算法通过设计合理的趋近律使观测量估计值与测量值的差值趋近于零，根据观测出的反电动势值计算转子位置和转速[5].该方法具有鲁棒性强、对模型参数变化的敏感性低等优点，许多学者对基于SMO的无位置传感器算法展开了研究.Peng等[6]在SMO算法的基础上设计锁相环从反电动势中解算转子位置和速度信号，以降低信号中的高频抖振；Kim等[7]为克服传统SMO算法中由于低通滤波器引入而产生的时间延迟问题，采用Sigmoid饱和函数代替开关函数获得了良好的观测效果；陈炜等[8]提出一种自适应滑模观测器算法对反电动势进行估计，改善了低速下转子位置和转速的估计效果；刘震等[9]采用二阶滑模理论设计反电动势观测器，减轻了观测系统的抖振并提高了响应速度.但上述这些无位置传感器算法的研究均是基于简化的PMSM等效电路模型，该模型以定子铜损作为电机运行中的唯一损耗而忽略铁芯损耗，基于简化模型开发的无位置传感器算法易造成转子位置定位不准、定子电压易饱和等问题[10]，苑婷等[11]重构PMSM铁损模型，在此模型的基础上应用SMO算法观测扩展反电动势实现无位置传感器控制.目前考虑PMSM铁损的无位置传感器算法的研究还比较少.

基于以上的研究现状，本文根据考虑铁损的PMSM等效电路模型，得到扭矩电流的状态微分表达式；分别在d-q轴系和α-β轴系下设计滑模观测器，估计转子转速和位置，在稳态条件和动态条件下进行了仿真分析；对不同轴系下得到的观测结果进行对比，提出了基于扩展卡尔曼滤波的融合算法，通过仿真与实验验证了算法的观测效果.

1 永磁同步电机铁损模型

1.1 铁损产生机理

电机在运行过程中，转子铁芯和定子铁芯中产生的损耗即为铁芯损耗，简称铁损.由Bertotti铁损分离模型可知，铁损按产生机理分为：涡流损耗、磁滞损耗和异常损耗[12]，只考虑铁芯中磁感应强度在大小上的变化，得到单位体积上的铁芯损耗功率为

(1)

式中:Ph为磁滞损耗，W/m3；Pc为涡流损耗，W/m3；Pa为异常损耗，W/m3；kh为铁芯的磁滞损耗系数，与材料和加工工艺相关；f为外加磁场的变化频率，Hz；Bm为磁感应强度幅值，T；kc为涡流损耗系数，与硅钢片的电导率、厚度和密度有关；ka为异常损耗系数.

由式(1)可见，铁芯损耗随外加磁场频率的增大而增大，即随电机转速的升高，铁芯损耗增大.且当电机转速逐渐升高时，铁芯损耗占电机总损耗的比重会越来越大[11]，这也是对调速性能要求更严格、电机控制系统不能忽略铁损的原因.

1.2 考虑铁损的PMSM等效电路模型

将铁芯损耗等效成在一铁芯内阻上产生的损耗，这个等效内阻即为铁损电阻.得到考虑铁损电阻的永磁同步电机在d-q轴上的等效电路模型如图1所示.图中d-q轴电流分量id/iq一部分流经铁损电阻Rf产生铁芯损耗，称为铁损电流idf/iqf；另一部分产生电磁转矩，称为扭矩电流idt/iqt.

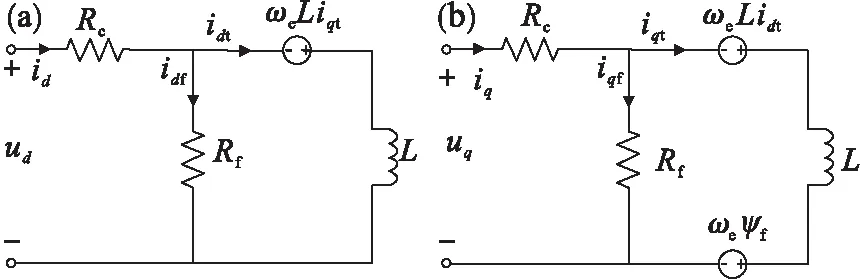
图1 考虑铁损电阻的PMSM等效电路图

根据图1分别写出d，q轴下的电压方程和电流方程为

(2)

(3)

式中：Rc为铜损电阻；L为d，q轴上的电感，表贴式转子结构的d，q轴电感相同；ωe为电机电角速度；ψf为永磁体磁链.

由式(2)和式(3)得到扭矩电流的微分方程为

(4)

该状态微分方程是考虑铁损的永磁同步电机无位置传感器控制算法研究的基础.

2 d-q轴系下的无位置传感器算法

滑模观测器算法的基本思路是以电流误差作为滑模面函数的输入，以反电动势E作为观测值，根据反电动势的观测值计算得到转速和转子位置信息.由于考虑铁损的PMSM模型建立在两相旋转坐标系(d-q轴系)下，本节在该轴系下设计滑模观测器进行无位置传感器算法研究.

2.1 滑模观测器设计

根据式(4)，将电流状态微分方程改写为

(5)

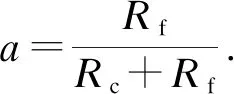
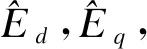
(6)

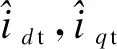
选取电流估计误差作为滑模面函数，如式(7)所示：

(7)

传统的滑模观测器选取开关函数构造反电动势观测值，但由于开关函数是一个不连续的函数，会造成反电动势观测结果的高频抖振，常增加低通滤波器以获得光滑的观测信号，但低通滤波器的引入会造成观测结果延迟，因此本文采用连续饱和的Sigmoid函数代替开关函数，该函数的表达式为

(8)

式中，α为一正实数.

反电动势观测值的表达式为

(9)

对式(6)和式(5)作差，得到电流误差的微分方程为

(10)

(11)

若想满足收敛条件，只需满足式(11)第二项恒小于等于0即可.将式(9)代入，式(11)的第二项可表示为

(12)

(13)

2.2 仿真结果分析

本文仿真所用电机为一台31 W的表贴式永磁同步电机，电机的部分参数：定子电阻为2.1 Ω，电感为1.4 mH，极对数为4，额定直流电压为24 V，额定电流为1.8 A，铁损电阻为(0.06ωe+50)(由试验测得)，应用Matlab/Simulink搭建的PMSM无位置传感器控制系统进行仿真.

其中，由电流传感器得到定子三相电流ia，ib，ic，经坐标变换得到id，iq，根据式(14)得到扭矩电流的测量值idt和iqt.

(14)

首先给定目标转速3 000 r/min，得到电机转速和转子位置的观测结果如图2所示.

由图2可以看出，转速观测值能够很好地跟随实际值，最大误差只有1 r/min，转子位置观测值由转速观测值积分得到，存在-0.12°的微小误差.

设定目标转速为500 r/min，验证电机控制系统在低速时的转速跟随情况，得到电机转速和转子位置的观测结果和误差如图3所示.对比图3与图2，在保证参数kq和α不变的前提下，目标转速较低时收敛相对缓慢，转速的观测误差在0.5 r/min以内，且转子位置的观测误差在-0.22°左右，精度足够，算法的鲁棒性较好.

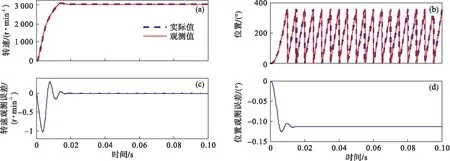
图2 3 000 r/min目标转速下观测结果及误差

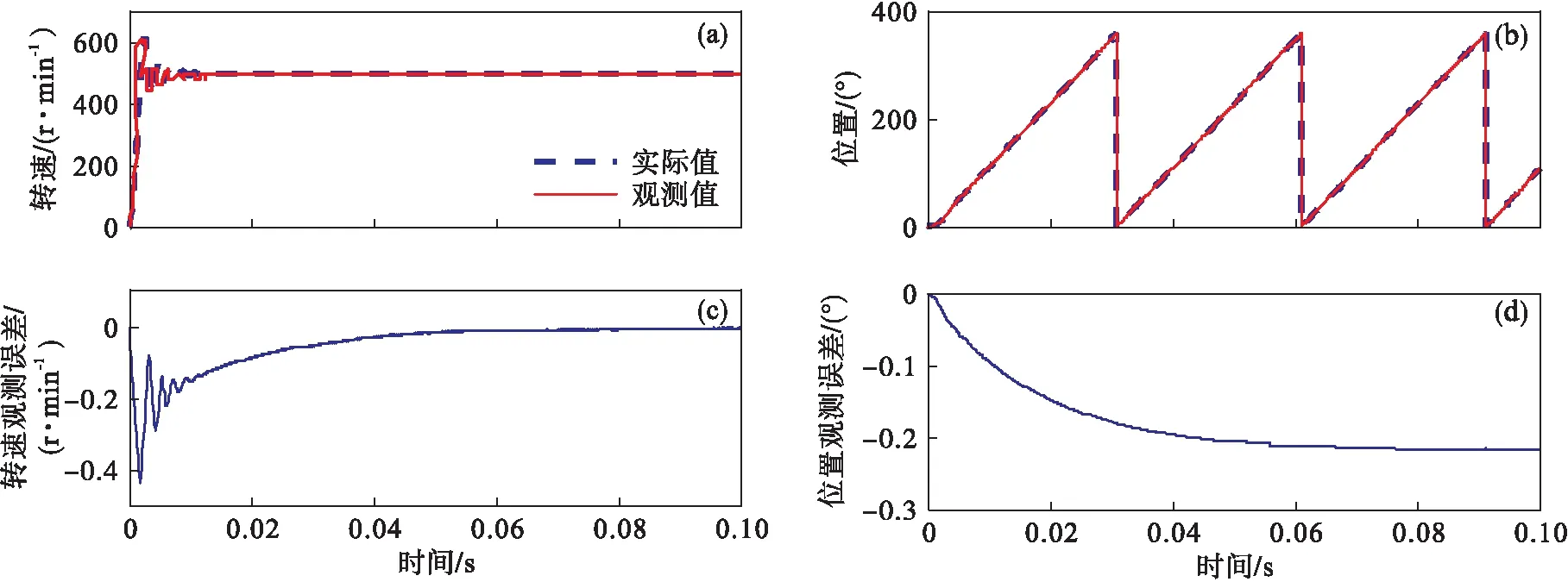
图3 目标转速为500 r/min下观测结果及误差

为了进一步验证滑模观测器的动态特性，分别在目标转速为0～3 000 r/min斜坡变化和3 000～500 r/min阶跃变化下进行仿真，得到无位置传感器算法的转速和转子位置观测结果如图4，图5所示.

图4 目标转速为0～3 000 r/min斜坡变化下观测结果及误差

由图4可看出，斜坡输入下转速观测值能持续跟随目标转速，转速误差最大为-0.5 r/min，转子位置误差最大为-0.15°.图5中在转速突然变化后，转速的估计值也能很好地跟随实际值，最大误差为-1 r/min，转子位置误差在-0.2°左右，不会影响到电机控制系统的稳定性，说明d-q轴系下设计的无位置传感器算法具有良好的动态特性.

图5 目标转速为3 000～500 r/min阶跃变化下观测结果及误差

3 α-β轴系下的无位置传感器算法

3.1 α-β轴系下的电机模型

首先推导α-β轴系下的扭矩电流状态微分表达式.根据式(2)和式(3)，得到电压状态方程的矩阵形式为

(15)

对式(15)进行反Park变换，反Park变换矩阵如式(16)所示，得到α-β轴系下的电压状态方程见式(17).

(16)

(17)

对式(17)进一步整理得到α-β轴系下的扭矩电流iαt和iβt的状态微分表达式为

(18)

对比式(18)和式(5)，α-β轴系下的扭矩电流状态方程没有两轴间的电流耦合，两轴上的反电动势既包含转子的转速信号，也包含位置信号，因此通过观测该轴系下的反电动势计算得到的转子位置信号，可以避免由转速积分带来的累计误差.

其中，针对扭矩电流的测量值iαt，iβt，由传感器直接测量的ia，ib和ic经过坐标变换得到iα和iβ后推导计算得到.其表达式为

(19)

3.2 滑模观测器设计

根据式(18)，两轴上的反电动势分量分别为Eα=-ωeψfsinθe，Eβ=ωeψfcosθe.根据式(18)建立观测器模型为

(20)

选取扭矩电流估计误差作为滑模面函数s，其微分表达式为

(21)

参照2.1节的设计思路，使用Sigmoid函数f(x)表示反电动势的估计值为

(22)

根据收敛准则，得到可调参数kα，kβ的收敛条件为kα，kβ≥ωeψf.

转子转速和位置的观测值通过式(23)计算得到：

(23)

3.3 仿真结果分析

当目标转速为3 000 r/min时，转子转速和位置的观测结果如图6所示.由图可见，α-β轴系下的观测结果中存在较大幅值的高频抖动现象.对比d-q轴系下的反电动势表达式，α-β轴系下的反电动势为一正弦(余弦)信号.由式(22)可知，由于铁损电阻的引入和电机控制系统中电流环的调节作用，难以保证扭矩电流误差信号为一标准的正弦信号，因此由电流误差信号观测得到的反电动势及由此算出的转速和转子位置信号存在高频抖振.

图6 3 000 r/min目标转速下观测结果及误差

图7为α-β轴上的电流信号及误差，由图7e,图7f放大图可以看出，电流信号中掺杂着不规则谐波.对比图2所示d-q轴系下的转速观测结果，d-q轴系下反电动势为一正比于转速的稳定信号，其电流估计误差也为稳定信号，因此转速观测信号稳定，观测效果较好.虽然α-β轴系下转速观测结果较差，但由于转子位置信号的观测值通过反三角函数计算得到，不依赖于转速信号，且在设计观测器时，两轴上并无耦合关系，因此转子位置的观测结果对比图2中d-q轴系下的观测结果，其观测误差最大值为0.06°，在0.02 s后，虽然存在高频抖振，但抖振幅值在0.005°左右，与实际信号误差很小，准确性较高.

3.4 基于EKF的融合观测算法

根据2.2节和3.3节的仿真分析结果可知，在d-q轴系下设计的算法可以较准确地观测出转速信号，但转子位置信号的观测值易产生累计误差；而在α-β轴系下得到的观测信号中含有不规则抖振，难以直接应用在电机控制系统，但位置观测信号的准确性较高.因此设计基于扩展卡尔曼滤波(extended Kalman filter，EKF)的融合观测算法，将α-β轴系下的转子位置信号中的抖振信号视作噪声，对其进行滤波处理获得可信性更高的转子位置信号.该方法首先将电机模型离散化，然后通过预测、计算卡尔曼增益、修正等环节得到转子位置和转速信号[14-15].

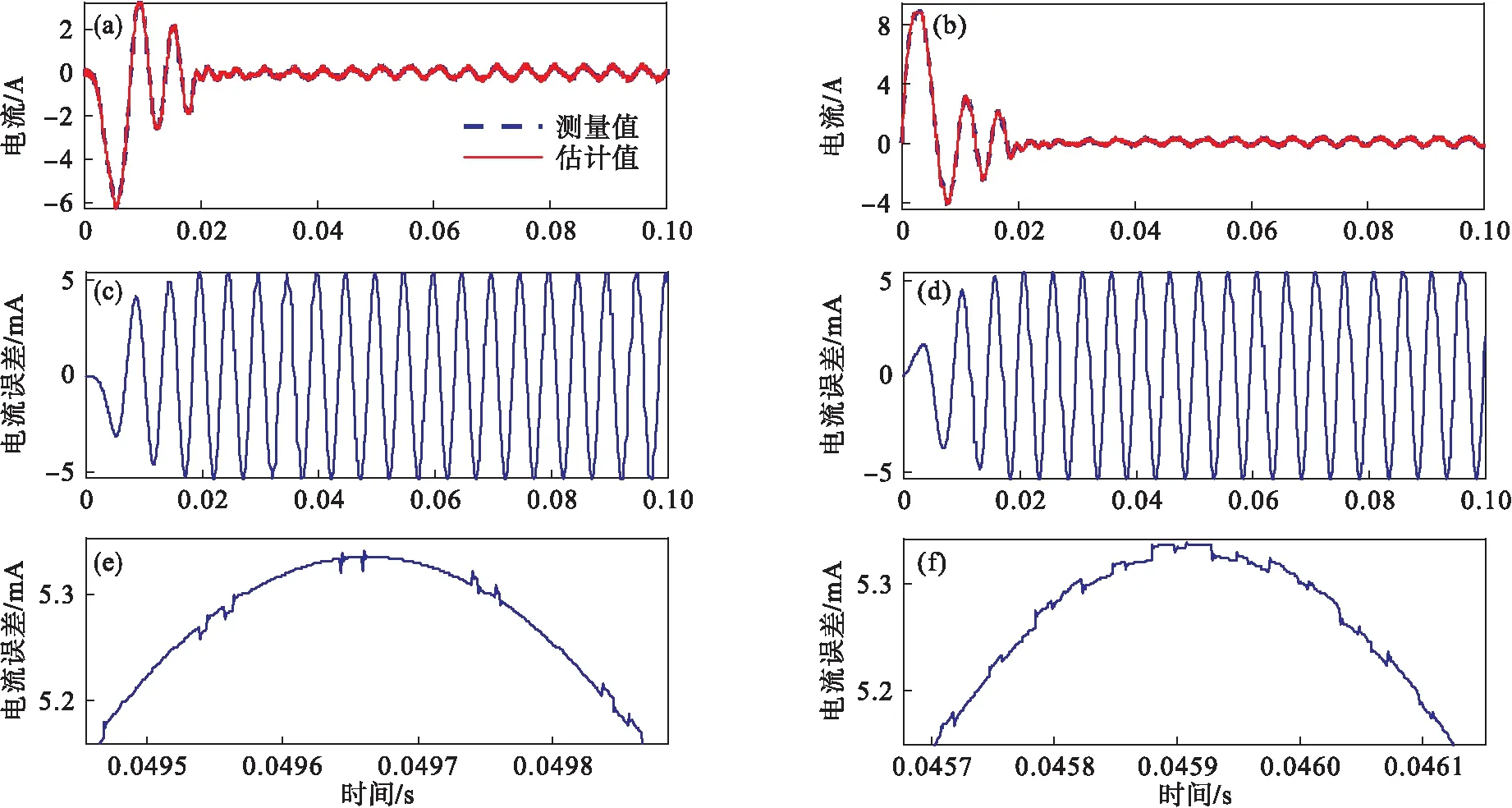
图7 电流信号观测结果及误差

(24)

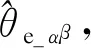
(25)

根据式(24)和式(25)，EKF算法可以表示为

(26)

P(k|k-1)=P(k-1|k-1)+Q,

(27)

(28)

(29)

P(k|k)=[1-K(k)]P(k|k-1).

(30)

其中：式(26)，式(27)为预测阶段方程；P(k|k-1)为第k步下误差协方差的预测值；Q为预测过程噪声的方差；式(28)为卡尔曼增益计算方程，R为V的方差；式(29)，式(30)为修正阶段方程.

式(29)即为卡尔曼滤波器最终输出的转子位置信号，转速信号仍采用d-q轴系下的观测值.为验证融合观测算法在电机长时间运行、工况发生改变后的观测效果，设置仿真时间为1 s的多变工况，采用d-q轴系下设计的观测算法与基于EKF的融合观测算法观测结果如图8和图9所示.

图8 基于d-q轴系的无位置传感器算法观测结果

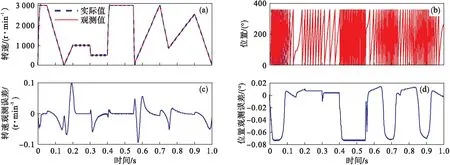
图9 基于EKF的融合观测算法观测结果

由观测结果可见，该仿真条件下基于d-q轴系的观测算法的转速观测误差最大值为1.2 r/min，转子位置观测误差最大值为-1.1°；采用融合观测算法得到转速观测误差最大值为0.1 r/min，位置观测误差最大值为-0.08°，误差缩小到原误差的10%以下.

4 实验分析

基于图10所示的硬件系统对基于EKF的融合观测算法进行实验验证，电机为仿真所用31 W表贴式永磁同步电机，内装有混合式光电编码器，用于验证无位置传感器观测算法的准确性.

图10 永磁同步电机实验硬件系统

首先应用Simulink软件搭建PMSM无位置传感器控制系统的各模块；然后进行数据管理与参数配置，对各模块进行编译生成代码；最后将生成的代码在CCS(code composer studio)软件环境下进行集成，编译进仿真器进行实验.

在转速控制模式下，PMSM的控制目标、传感器测量和由无位置传感器观测到的转速对比曲线及其细节放大图如图11所示，由传感器测得的转子位置与融合观测算法得到的转子位置误差曲线如图12所示.

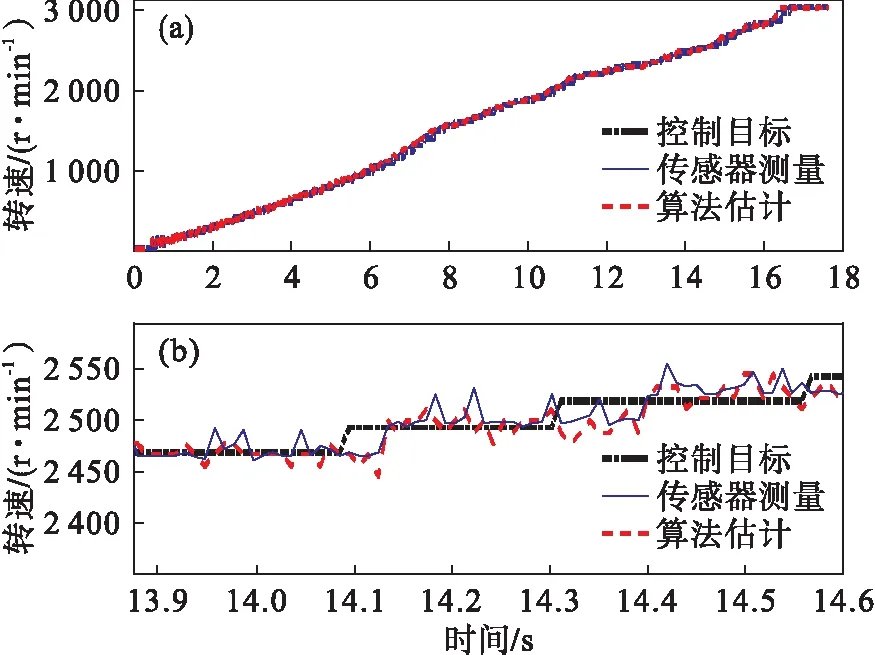
图11 转速结果对比

图12 转子位置误差

在电机的实际控制系统中，由于逆变器的死区效应、电机本体永磁体磁场的设计偏差与工艺限制等影响，都会在电机的输出转矩和转速中引入谐波，从而导致电机实际输出转速在目标转速附近存在波动，而在电机的仿真系统中这些因素的影响均被忽略，同时，传感器也会存在一定的测量误差.由传感器测得和基于EKF融合观测算法得到的转子位置误差在±3°范围内，电机转速实验结果统计如表1所示.由表1可见，传感器测量转速相比于目标转速的平均误差率为0.299%，基于EKF融合观测算法观测转速相比于目标转速的平均误差率为0.32%，传感器与融合观测算法的相对误差率为0.021%，对比图9的仿真结果，转速误差率最大值为0.01%，实验结果相比仿真结果误差增大，但仍保证了较高的准确性.实验结果说明所提出的基于EKF的融合观测算法能达到与传感器相当的效果，可用于实际的电机控制系统.

表1 机械转速实验结果统计

5 结 论

1) 针对考虑铁损的PMSM等效电路模型，分别在d-q轴系和α-β轴系设计滑模观测器进行无位置传感器算法研究.在两轴系下搭建了观测器模型并进行了仿真验证.结果表明，d-q轴系下的无位置传感器算法得到的转速观测信号准确度高、鲁棒性好、动态特性良好，但转子位置信号易产生累计误差；α-β轴系下的无位置传感器算法得到的观测信号存在高频抖振，难以应用于电机控制系统，但转子位置信号的准确度更高.

2) 采用卡尔曼滤波器对两轴系下的观测信号进行融合，得到可信度更高的转子位置信号.仿真结果表明：基于EKF的融合观测算法对比d-q轴系下的SMO算法，观测结果误差小，观测信号中不存在高频抖振.融合观测算法实验表明：由传感器测量和融合观测算法得到的转速其相对转速误差率较小，验证了基于EKF的融合观测算法的有效性，具有实际应用价值.