特征特定标记关联挖掘的类属属性学习

程玉胜 张露露 王一宾 裴根生

1(安庆师范大学计算机与信息学院 安徽安庆 246133)

2(计算智能与信号处理教育部重点实验室(安徽大学) 合肥 230601)(chengyshaq@163.com)

随着信息技术的高速发展，多标记学习已经成为数据挖掘领域和机器学习领域的研究热点之一.不同于传统单标记学习中单个示例仅与一个标记相关联；而在多标记学习中，每个示例则与多个标记相关联.例如，一部小说可能既属于穿越小说又属于科幻小说；一幅图画可能同时有“蓝天”“白云”“大海”等多个信息标注.这种学习框架更加符合自然世界中对象的多义性，因此被广泛应用于情感分析[1-3]、图像标注[4-6]、文本分类[7-8]和生物信息学[9]等领域.但目前多标记学习仍然存在很大挑战，不同于单标记空间，多标记空间具有很高的复杂度，处理高维多标记特征数据以及解决标记之间的相关性成为目前多标记学习的两大挑战.

在多标记分类学习中，学者们已提出多种学习算法，通常分为3类：问题转换方法、算法适应方法和集成学习方法.问题转换方法[10-13]直接将多标记学习问题简化成多个独立的单标记学习问题，此类方法忽略标记间相关性，导致分类效果欠佳，常见的问题转化方法有BR(binary relevance)算法[12]、LP(label powerset)算法[13]等.算法适应方法[14-17]是通过对常用的监督学习算法进行改进以适应多标记学习任务，该方法具有较高的分类性能，常用的算法适应方法有MLkNN(multi-labelk-nearest neighbor)算法[14]和RANK-SVM(ranking support vector machine)算法[17]等.集成学习方法[18-20]利用多个基学习器组合以提升分类器的泛化能力，代表算法有CC(classifier chain)算法[19]和BoosTexter(boosting-based system for text categorization)算法[20].在处理多标记数据时，上述方法均采用了相同的策略，即通过多标记相同的属性集合预测所有的类别标记.尽管此方法在多标记研究领域取得了较大成功，但所有标记由相同的属性决定并不合理.每个类标记应该具有其自己的特征，并且由对该标记最具辨别力的一些特定特征确定.例如，在区分患者是否患有糖尿病时，血常规中血糖这一特征项具有决定性作用，但却无法判断该患者的性别.所以在多标记学习中某些标记可能只由其自身的某些特有属性决定，这些特定属性被称之为标记的类属属性.利用类属属性进行多标记学习能够有效地提升分类精度，并且可以避免多标记数据维度过高而导致的“维数灾难”问题，使多标记学习结果鲁棒性更强.但目前类属属性学习算法仅从标记角度考虑标记相关性提取重要特征，虽然在一定程度上取得了成功，却忽略了从特征角度去提取重要标记.例如，若从颜色属性去考虑标记，则很容易将“蓝天”和“白云”联系起来，寻找到某个属性的独有标记，得到标记间的相关关系.

基于上述分析，本文提出了一种新型的类属属性多标记学习算法，即从特征的角度去提取重要标记.由于某个特征与标记空间中的某些标记可能存在很强的联系，这些标记则是该特征的重要标记.

本文的主要贡献有4个方面：

1) 通过在特征层面考虑特征对应的重要标记与在标记层面考虑标记对应的重要特征(类属属性)进行联合学习，提出了特征特定标记关联挖掘的类属属性学习算法(label-specific features learning for feature-specific labels association mining, LSFFSL).

2) 为充分挖掘特征的重要标记，本文利用信息熵中的互信息理论，构建特征标记矩阵.从特征的角度挖掘其重要标记，进而得到标记之间的相关信息，避免了传统算法中从全部标记空间考虑标记相关性导致的计算复杂性问题.

3) 将弹性网络正则化理论添加到极限学习机损失函数中，将特征标记相关性矩阵作为L2正则化项，利用L1正则化项提取类属属性.

4) 在11个基准多标记数据集中与目前先进的多标记算法进行对比，实验结果表明本文算法在多标记分类中具有良好的分类效果.

1 相关工作

在众多领域中多标记学习具有广阔的应用背景，但同时也存在巨大的挑战.标记相关性和数据高维性等问题是目前多标记学习的热点研究课题.利用类属属性进行多标记学习可以有效处理数据高维性.其中，融入标记相关性的类属属性学习能有效提升多标记的学习性能.针对标记相关性和类属属性学习，学者们已提出了大量的学习算法.

首先，标记相关性的学习是当前多标记学习研究的热点问题之一，标记相关性算法一般分为3类，分别是一阶算法、二阶算法和高阶算法.一阶算法主要是将多标记学习问题转化为多个单标记问题进行求解，例如BR算法[12]、MLkNN算法[14]和ML-EKELM(multi-label learning algorithm of elastic net kernel extreme learning machine)算法[21]等分别利用支持向量机(support vector machine, SVM)、最近邻(k-nearest neighbor, KNN)和弹性网络核极限学习机(kernel extreme learning machine, KELM)分类器进行多标记分类.但该策略将各标记看作是独立的，忽略了标记之间的相关性.二阶算法将多标记学习问题转化为“标记排序”[22-24]问题求解，考虑2个标记间内在相关性时，相比一阶策略算法的泛化能力有较大提高，算法有CLR(calibrated label ranking)算法[23]和LPLC(local pairwise label correlation)算法[24]等.然而现实世界对象的多义性使得二阶算法无法较好地表达标记之间的相关性.而高阶算法考虑所有标记之间的相关性，能更好地反映现实世界标记之间的复杂关系，常用算法有CC算法[19]和EbCC(ensembles of classifier chains)算法[25]等.但高阶方法具有很高的复杂度，当数据中标记数较多时处理效率较低.

而对于类属属性的学习，传统的多标记学习中标记都是由相同的属性集合进行预测，忽略了标记自身的某些特征.基于此，Zhang等人[26]和吴磊等人[27]提出了基于类属属性的多标记学习算法(multi-label learning with label-specific features, LIFT)，该算法先利用k-means聚类技术应用于每个标记的正负训练样本，然后利用SVM方法对多标记分类进行建模，在解决多标记分类问题上取得了显著成效.Xu等人[28]考虑到通过LIFT算法构建标记类属属性可能会导致特征向量维度增加，特征空间存在冗余信息，提出了基于模糊粗糙集进行类属属性约简的算法(learning label-specific reduction based on fuzzy rough set, FRS-LIFT)和基于样本选择的类属属性约简算法(learning label-specific reduction based on fuzzy rough set by sample selection, FRS-SS-LIFT).LIFT是一种合理有效的学习算法，然而这种算法忽略了标记相关性的影响，因此Huang等人[29]提出学习类属属性和类独立标记的多标记学习算法(learning label-specific features and class-dependent labels, LLSF-DL)，通过特征L1正则稀疏约束和标记相关性信息求解类属属性矩阵和类标记独立矩阵，该算法通过设计优化框架来学习每个标记的低维数据表示，并利用成对标记相关性考虑共享特征.Weng等人[30]在LIFT算法的基础上提出了基于类属属性和局部成对标记相关性的多标记学习算法(multi-label learning based on label-specific features and local pairwise label correlation, LF-LPLC)，该算法只考虑局部成对标记之间的相关性.Zhang等人[31]通过类属属性和多标记联合学习(multi-label learning with label-specific features by resolving label correlations, MLFC)，该算法的关键是设计一个优化模型来分配特征权重，同时构建附加特征来考虑标记之间的相关性.

2 基础概念

2.1 信息熵

熵在信息论中是指随机变量的一种不确定性的度量，而信息熵是度量随机变量不确定性的程度，变量的不确定性越大信息熵也越大，信息熵也指信息量的期望.

定义1[32].信息熵.假设有一个随机变量A={a1,a2,…,aq}，其不确定期望为

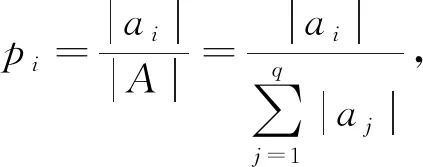
(1)

在多标记学习中，传统信息熵常被用于特征选择.但传统信息熵不具有补的性质，利用粗糙集理论中等价划分的思想，引入模糊信息熵的概念.

定义2[33-34].模糊信息熵.假设信息系统由样本及其对应的特征所描述，把样本空间的描述记为论域U，根据某种特征属性可以对论域U进行划分.假设按照特征属性集合F={f1,f2,…,fn}对论域U进行划分，记UF={A1,A2,…,Am}.按标记属性对论域U进行划分,记为B={B1,B2,…,Bn}.则模糊信息熵的定义为

E(A)=

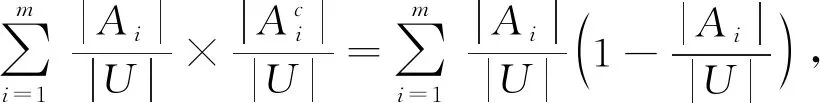
(2)

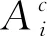
(3)

模糊信息熵的计算只限于单随机变量，现实问题的信息系统中一般涉及多个随机变量，本文考虑2个标记之间的相关性，因此利用互信息的相关理论.互信息表示2个随机变量重复的信息量，即2个随机变量的相关性.互信息越大表示2个变量的相关性越大，给出模糊互信息的定义：

定义3[33-34].模糊互信息.模糊联合信息熵定义为

即模糊互信息可以利用自信息和联合熵表示为

I(A;B)=E(A)+E(B)-E(A,B).

(4)

2.2 极限学习机

传统的神经网络算法需要设置更多的网络参数，处理最优解问题时很可能会出现局部最优解，以至无法获得全局最优解.极限学习机(extreme learning machine, ELM)则是一种有效求解单隐藏层前馈神经网络(single-hidden layer feedforward neural network, SLFN)的优化算法，只需设置隐藏层节点的数量，同时随机初始化权重和偏置来解决全局最优解.ELM具有求解速度快、泛化性能高等特点，在监督学习[35-37](分类、回归)和无监督学习[38-39](聚类)等方面得到广泛应用.

在进行问题求解之前，需作出形式化定义：设有n个任意样本{(Xi,Yi)|i=1,2,…,n}，其中特征空间表示为Xi=(xi1,xi2,…,xi d)T，标记空间为Yi=(yi1,yi2,…,yi m)T，则L个隐藏节点的SLFN形式化定义为

(5)

其中，βi=(βi1,βi2,…,βi m)T为输出权值，gi为激活函数，表示第i个隐藏节点输出，定义为

gi(Xj)=g(wi·Xj+bi),

(6)

其中，wi=(wi1,wi2,…,wi d)T表示输入权值，第i个隐藏神经元的偏置表示为bi，“·”为点积，激活函数使用sigmoid函数约束输出范围以实现分类任务.

通过上述随机特征映射，构建以最小化平方误差式的近似误差来求解输出权值β.最小化目标表达式为

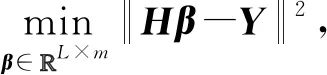
(7)

其中，H表示隐藏层的输出矩阵(随机矩阵)，定义为

(8)

而式(7)中Y为数据中标记矩阵：

(9)

联合式(5)～(7)，目标函数最小二乘解可表示为

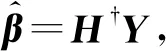
(10)

其中，H†表示式(8)中H的Moore-Penrose广义逆矩阵，进一步可表示为

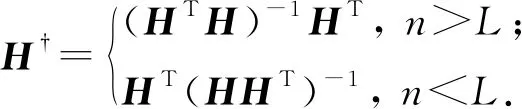
(11)

最终，式(5)用矩阵可以表示为

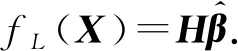
(12)

3 基于类属属性新型多标记学习算法

3.1 特征特定标记挖掘

不同于单标记学习各标记互斥，在多标记学习中每个示例与多个标记相关联，而各标记之间存在一定联系，因此标记相关性分析是多标记学习中需重点考虑的问题.在某种程度上特征决定了标记的种类和个数，因此标记相关性分析若单纯只从标记空间考虑显然并不合理.但传统的类属属性学习算法仅在标记空间中考虑其特定特征,未考虑特征对标记的影响.由于某些特征可能仅对部分标记起决定性作用，而其他标记并不受该类特征影响.若我们能够从特征空间中提前关注特征所对应的重要标记，则更易获取标记之间的相关性信息.基于这种现象，本文通过从特征的角度发掘其重要标记，摒弃了从全部标记空间考虑标记相关性，进而避免了传统标记相关性计算复杂性.该算法与通过标记提取重要特征类属属性学习恰好相反，即站在特征的角度去提取重要标记.为了挖掘这一信息，本文采用信息熵理论提取特征标记矩阵.

Table 1 Definition of Multi-Label Data

表2展示了当m=4和d=5的虚拟多标记数据，通过式(4)模糊互信息计算公式求得特征与标记之间的矩阵Flabel(feature-label correlation matrix).

Table 2 Feature-Label Matrix of Multi-Label Data

通过表2发现，若将特征-标记矩阵按列分析，每个标记对于特征的重要程度不同.我们选取特征-标记矩阵中权值比较大(大于0.1)的标记作为特征的重要标记.因此，得出特征f1的重要标记为l1和l2，同理特征f5的重要标记为l1，l2，l3.

由于其他距离度量方法无法准确描述2个向量在方向上的差异，因此本文采用余弦相似度这种度量方法描述多标记中标记之间的相关关系.但不同于其他算法仅在原标记空间利用余弦相似度构建标记空间Y的相关性矩阵，本文则通过构建出的Flabel矩阵计算余弦相似度，构建特征标记相关矩阵，计算方法为

(13)

其中，fl是矩阵Flabel的元素;j=1,2,…,m;k=1,2,…,m.Rjk≠0表示2个标记之间具有相关性，Rjk=0则表示2标记无相关性，且|Rjk|越大则相关性越强.

3.2 联合特征特定标记的类属属性模型构建

目前，类属属性学习仅站在标记的角度去选择其重要的特征，忽略了特征对标记的影响.事实上，某个特征仅与标记空间中的某些标记存在很强的联系，这些标记则是该特征的重要标记，称之为特征特定标记.因此，本文构建了联合特征特定标记的类属属性学习模型，从特征层面提取重要标记与从标记层面提取重要特征进行双向联合学习.

首先，在建立LSFFSL模型中，应用极限学习机构建初始化优化函数.随后，考虑特征层面提取重要标记，将构建的特征标记相关矩阵加入到优化目标函数中.最后，为了得到特征的稀疏化表达，同时避免Lasso凸性不严格导致的多解问题[40]，我们通过重构弹性网络正则化约束极限学习机[21]目标函数.因此，特征特定标记和类属属性联合模型表达式为

(14)

其中，L1正则化项以稀疏化β，使其在各标记的特征分量中置0，达到选择各标记的类属属性作用；将特征标记相关性矩阵作为L2正则化项，以考虑标记的成对相关性.式(14)中C为惩罚因子，α参数控制特征标记相关性，λ控制稀疏化程度.由于目标函数F(β)为凸优化问题，存在L1范数导致问题非光滑.因此，将原问题看作一般带有L1范数的优化目标表示为

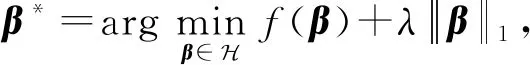
(15)

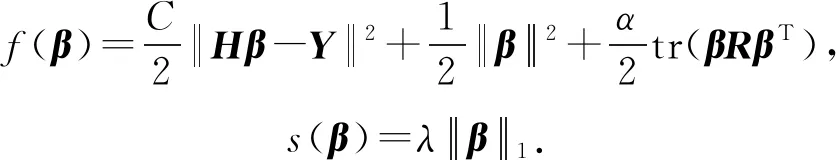
(16)

由于f(β)为凸光滑函数，且满足Lipschitz条件，即

(17)

由此，该问题即可采用近端梯度下降(proximal gradient descent, PGD)[41]进行问题求解.PGD算法属于贪心最小化迭代策略算法，对于基于L1范数的最小化问题能够快速求解.

将f(β)在βt附近进行二阶泰勒展开近似表达为

(18)

其中，z表示为

z

(19)

最终，求解式(18)可以得到迭代式：

(20)

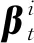
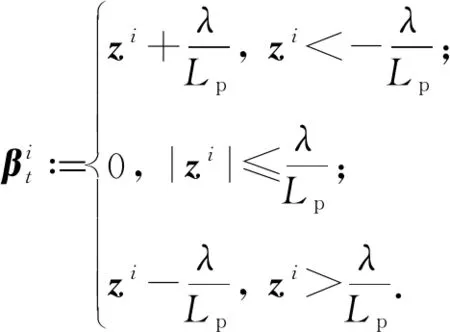
(21)

(22)

通过式(18)，β求解可以表示为

(23)

因此，式(23)需要求得Lipschitz常数Lp，根据式(22)求解过程表示为

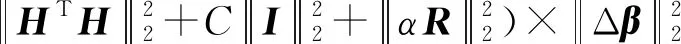
(24)

其中Δβ=β1-β2，Lipschitz常数Lp表示为

(25)

通过PGD求解出目标函数F(β)输出权值β，详细算法流程见算法1所示:

算法1.LSFFSL算法求解.

输出：预测标记Y*.

① 通过式(4)构造特征-标记矩阵Flabel；

② 根据式(13)构建特征标记的相关矩阵R；

③ 通过式(25)计算Lipschitz常数Lp；

④ 通过式(8)计算L个节点的特征映射H；

⑤ 通过式(16)计算

⑥ Repeat

⑦z

⑨ Until迭代停止；

⑩β*←βt+1；

3.3 算法时间复杂度

4 实验及结果分析

4.1 数据描述

为验证所提算法的有效性，本文选择Mulan Library(1)数据集下载地址为http:mulan.sourceforge.netdatasets-mlc.html.中11个公开基准多标记数据集，如表3所示.其中，Emotions数据集为某音乐学院男性的音乐剪辑，其包含593个示例，并由72个特征和6个标记所描述.Genbase数据集描述了662种蛋白质，每种蛋白质由1 186个特征描述，总共具有27种结构类别.Medical数据集为临床医学诊断文本，由1 449个特征描述978个示例，关联45个标记.Arts，Computers，Education，Science，Social，Society这6个网页文本数据集来自Yahoo网站，各数据均包含5 000个文本，特征为不同词汇在文本中的频率，标记为各文本的类别.Corel5k包含50个语义主题，各语义主题包含100张图片，共计5 000张图片.

Table 3 Multi-Label Data Sets

4.2 评价指标及实验设置

为比较本文算法LSFFSL的算法性能，实验采用MLkNN算法[14]、MLNB(multi-label naive Bayes)算法[15]、LIFT算法[26]、LLSF-DL算法[29]、MLFC算法[31]等作为对比算法，使用10折交叉验证进行实验.其中，MLkNN和MLNB算法为经典多标记学习算法，并且MLNB具有特征选择功能，而其余3个算法都是基于类属属性的先进多标记学习算法.在对比实验中，各对比算法参数均按照原论文参数范围设置，MLkNN近邻k=10，平滑系数s=1；MLNB的PCA(principal components analysis)比例r=0.3；LIFT聚类比率在[0.1∶0.1∶1]之间，最终比率r=0.2；LLSF-DL算法参数设置与原论文提及数据集的参数给与设定，对于原文未提及的数据集采用10折交叉验证取最好参数，其中参数α，β，γ∈{4-5,4-4,…,44,45}，ρ∈{0.1,1,10}；MLFC算法参数α，β，γ在全部数据集中均设置为1,0.1和0.1；本文算法隐藏节点L∈{400,600,800,1 000}，惩罚因子C∈{22,23,24}，参数α和λ∈{2-4,2-6,2-8,2-10}.

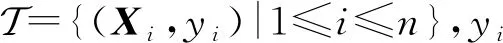
其中Δ为2个集合间的对称差.海明损失为对象标记错分次数情况，即将正确标记预测错误时的情况.当HLD(h)=0时为最好的情况，即HLD(h)越小，h(·)的性能越高.

1-错误率则是评估对象最高排位标记且错分正确标记的次数情况.当OED(f)=0为表示最好，即OED(f)值越小，f(·)的分类性能越高.

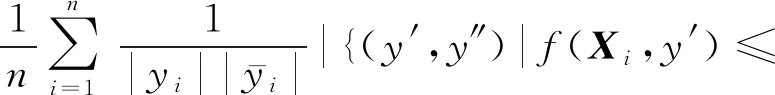
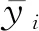
排序损失是评估对象非属的标记高于所属标记排位的次数情况.当RLD(f)=0时为最好情况，即RLD(f)越小，f(·)的性能越高.

平均精度为相关标记的排序分数高于特定标记y∈yi的情况评估. 其中，y′为yi的相关标记.当APD(f)=1时情况最好，即APD(f)值越大，f(·)的性能越高.

4.3 参数敏感性分析

本文所提算法存在4个参数：隐藏节点数L、惩罚因子C、标记相关性参数α和稀疏控制参数λ.本文选取数据集Medical，Yeast，Arts(数据分成训练集和测试集)，评价指标采用HL和AP进行参数敏感性实验分析.首先固定α=2-4和λ=2-4，对参数L和C进行敏感性分析，实验结果如图1所示：

Fig. 1 Parameter sensitivity analysis of L and C

通过图1(a)和图1(d)发现Medical数据集中惩罚因子C对结果影响较小，而隐藏节点数L=1 000时评价指标较好；分析图1(b)和图1(e)发现对于Yeast数据集，当隐藏节点数L=800，C=23时实验结果较好；对于Arts数据集，图1(c)和图1(f)表明隐藏节点数L=1 000，C=22时综合性能较好.

通过对参数L和C的敏感性实验，将参数L和C设置为各数据性能最优时的组合，再进行参数α和λ敏感性分析实验，实验结果如图2所示.

通过分析图2(a)、图2(b)和图2(c)可以发现当α=2-4时HL在3个数据集中普遍较小，在Medical和Yeast数据集中当λ=2-6达到最优，在Arts数据集中当λ=2-4达到最优；针对AP指标，分析图2(d)、图2(e)和图2(f)表明α=2-6，λ=2-10时在Medical数据集中最优，在Yeast数据集中α=2-4，λ=2-6达到最优，当α=2-4，λ=2-4时在Arts数据集中最优.

综合分析图1和图2得出，不同的数据集具有不同的最优参数组合，因此本文以下实验将在训练集中通过5折交叉验证寻找最优参数组合.

Fig. 2 Parameter sensitivity analysis of α and λ

4.4 结果分析

在11个多标记数据集中的对比实验结果如表4～7所示，分别对应HL，OE，RL，AP指标.评价指标中“↑”表示指标数值越高越好，“↓”表示指标数值越低越好，其中包括各指标的均值和标准差，各数据集中指标表现最优的用加粗字体表示.同时，为了更加明确各算法性能差异，本文使用显著性水平5%的成对t检验[42]进行算法对比，并在表格中使用●○表示本文算法LSFFSL优于差于对比算法，最后在各表格最后给出wintieloss，“win”表示LSFFSL优于该对比算法，“tie”表示无显著性差异，“loss”表示LSFFSL差于该对比算法.

表4给出了6种算法在海明损失的实验结果，可以看出LSFFSL算法仅在Art数据集中劣于LIFT算法；在Genbase数据集中与LIFT，LLSF-DL，MLFC算法无显著性差异；在Corel5k数据集中与MLkNN，LIFT，LLSF-DL，MLFC算法无显著性差异；在Emotion，Medical，Yeast，Computers，Education，Science，Social，Society这8个数据集中均占优.

表5是6种算法的1-错误率对比结果，除Genbase数据集中与LLSF-DL无显著性差异及Yeast数据集差于MLFC算法，所提LSFFSL算法均取得较好结果.

对比实验中排序损失结果如表6所示，LSFFSL算法仅在Education和Corel5k数据集上劣于MLKNN算法，在剩余9个数据集上结果均占优；与MLNB算法相比，本文算法LSFFSL在Genbase，Education，Corel5k这3个数据集上结果较差；在Arts数据集中相比于LIFT算法分类效果不显著，但在其他10个数据集均优于LIFT算法；同时，LSFFSL算法在11个数据集上均优于LLSF-DL算法；在Corel5k数据集上稍劣于MLFC算法之外，在其他的10个数据集较MLFC算法均占优.

6个对比算法的平均精度指标对比结果由表7所示，可以看出LSFFSL算法在除Medical数据集中不如MLFC算法，与其他5种对比算法在11个数据集中占有绝对优势.

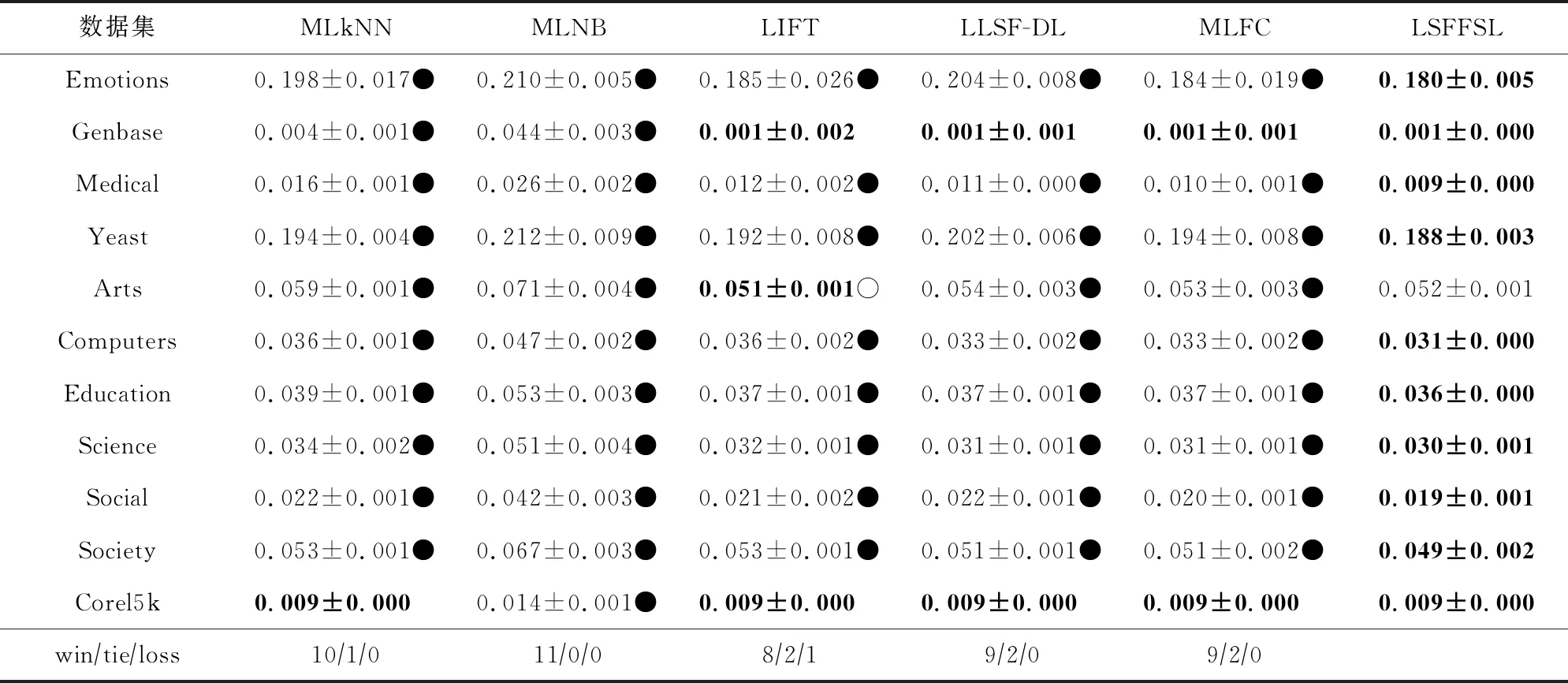
Table 4 Test Results of Six Algorithms in Terms of Hamming Loss(mean↓±std)

Table 5 Test Results of Six Algorithms in Terms of One-Error(mean↓± std)

Table 6 Test Results of Six Algorithms in Terms of Ranking Loss(mean↓±std)

Table 7 Test Results of Six Algorithms in Terms of Average Precision(mean↑± std)

为更加清晰展示所提算法在11个数据集上的综合性能，采用显著性水平5%的Nemenyi检验[26,43]进行统计假设检验.若2个对比算法的平均排序差值大于临界差(critical difference,CD)，则说明2个算法具有显著性差异，否则无显著性差异.图3展示了各对比算法在4个评价指标中的结果，其中CD=2.273 5.其中2种算法之间无显著性差异用加粗实线相连，图3的4个子图中，各算法性能从右到左依次降低.

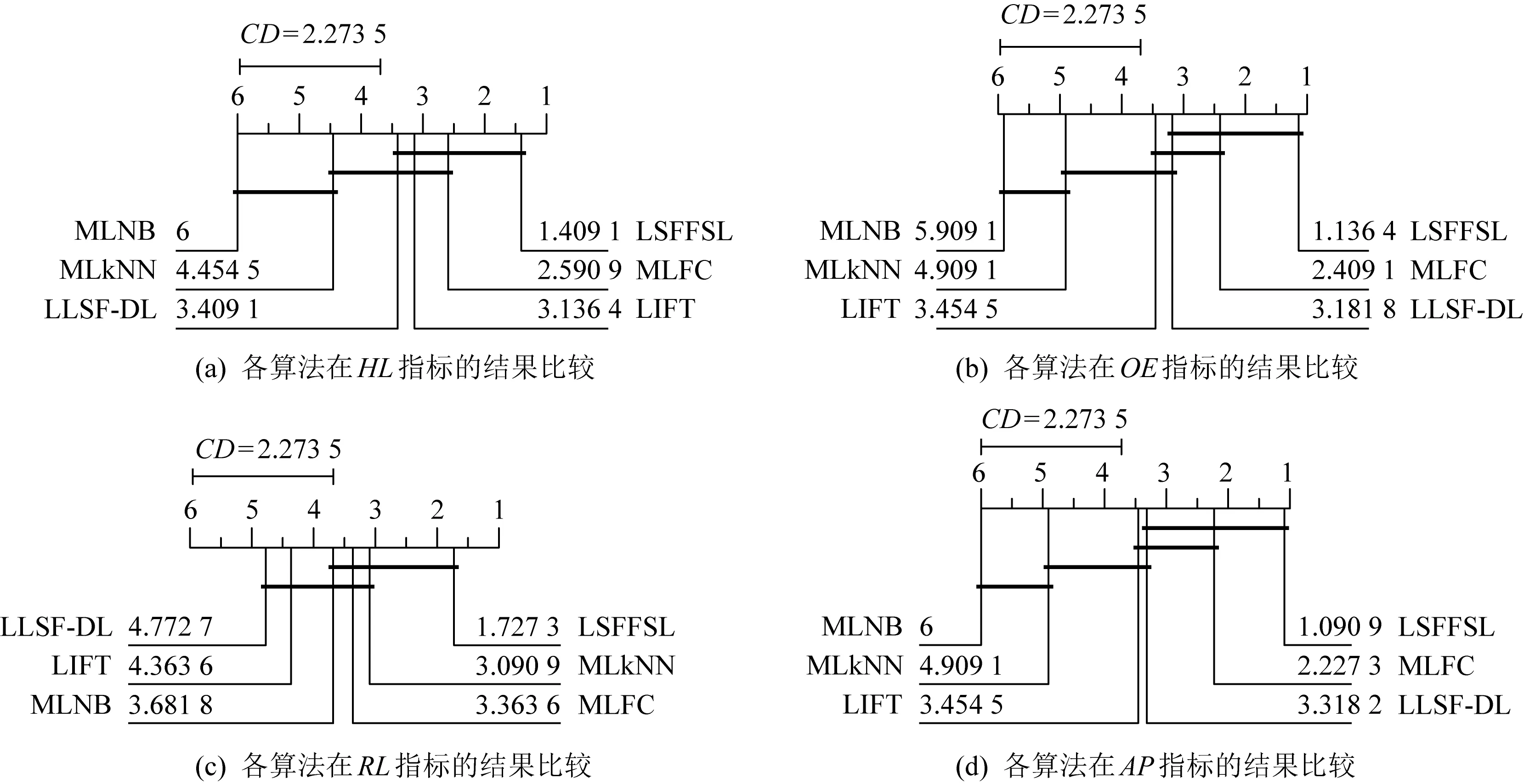
Fig. 3 The performance comparison of six algorithms

对每个对比算法，均有20个(5个对比算法，4个评价指标)结果进行比较，如图3所示.

1) 在LSFFSL算法中，如图3(a)在海明损失评价指标上，LSFFSL与MLFC，LIFT，LLSF-DL性能相比无显著性差异，与MLkNN，MLNB有显著性差异.如图3(b)在1-错误率评价指标上，LSFFSL与MLFC，LLSF-DL算法无显著性差异，与LIFT，MLkNN，MLNB有显著性差异.如图3(c)在排序损失指标上，LSFFSL与MLkNN，MLFC，MLNB算法无显著性差异，与LIFT，LLSF-DL有显著性差异.如图3(d)在平均精度指标上，LSFFSL与MLFC，LLSF-DL算法在统计上无显著性差异，与LIFT，MLkNN，MLNB有显著性差异.因此，LSFFSL在50%情况下与其他算法性能无显著性差异，在50%的水平下在统计上优于其他算法.

2) 针对MLFC算法，在统计上有25%优于其他算法，与其他算法在75%的情况下均无显著性差异.

3) 对LLSF-DL算法，有15%优于其他算法，在80%水平下和其他算法没有明显差异，有5%的情况差于其他算法.

4) 关于LIFT算法，在统计上优于其他算法占15%，与其他算法在70%的情况下无显著性差异，在15%的情况差于其他算法.

通过以上综合分析得出，LSFFSL算法具有最优性能，在50%的水平下优于其他算法.MLFC算法排名第二，在25%的水平下优于其他算法.第三是LLSF-DL算法，在15%的水平下比其他算法占优.综合以上实验结果分析，进一步体现了本文所提算法LSFFSL具有良好的性能.

5 结束语

与许多仅在标记空间处理标记相关性的算法不同，本文则从特征的角度考虑标记之间的相关性，提取特定特征的重要标记，将其与类属属性进行联合学习，提出了一种新型的类属属性学习算法.通过以极限学习机为初始算法构建模型，借助弹性网络和信息熵理论对模型进行优化.并通过在标准数据集中与目前先进的多标记算法对比，验证了算法的有效性和稳定性.但如何快速高效地选择分辨特征处理标记相关性问题则是未来进一步研究的重点.