基于SLPA优化的重叠社区发现算法
2021-01-15陈界全王占全汤敏伟
陈界全 王占全* 李 真 汤敏伟
1(华东理工大学信息科学与工程学院 上海 200237) 2(天翼电子商务有限公司风险管理部 上海 200080)
0 引 言
社区检测是一种在网络中探索集群或社区的行为。集群或者社区是一组紧密连接的实体,它们在组内的连接比与其他实体的连接更高[1]。对各种领域的真实网络进行社区的发现,对于理解复杂网络的结构和模式起着重要的作用。例如,在社交网络领域,可以根据不同的兴趣和背景将其划分为不同的社会群体进行准确的推荐;在生物学领域,传播网络由疾病和病毒两部分组成,通过对其进行研究和分析,找到易感染人群的关键社区或关键节点,预测传播路径,从而及时控制疾病。综上所述,社区检测在复杂网络的研究中有重要意义。
然而,目前的研究主要集中在检测非重叠的社区,然而真实社交网络中的社区通常是互相重叠的[2]。例如,一个研究者可能属于多个研究群组中,一个人在现实生活或者网络中会加入多个兴趣小组。所以,重叠社区的发现对于进一步分析和利用复杂网络结构具有重要的意义,重叠社区如图1所示。
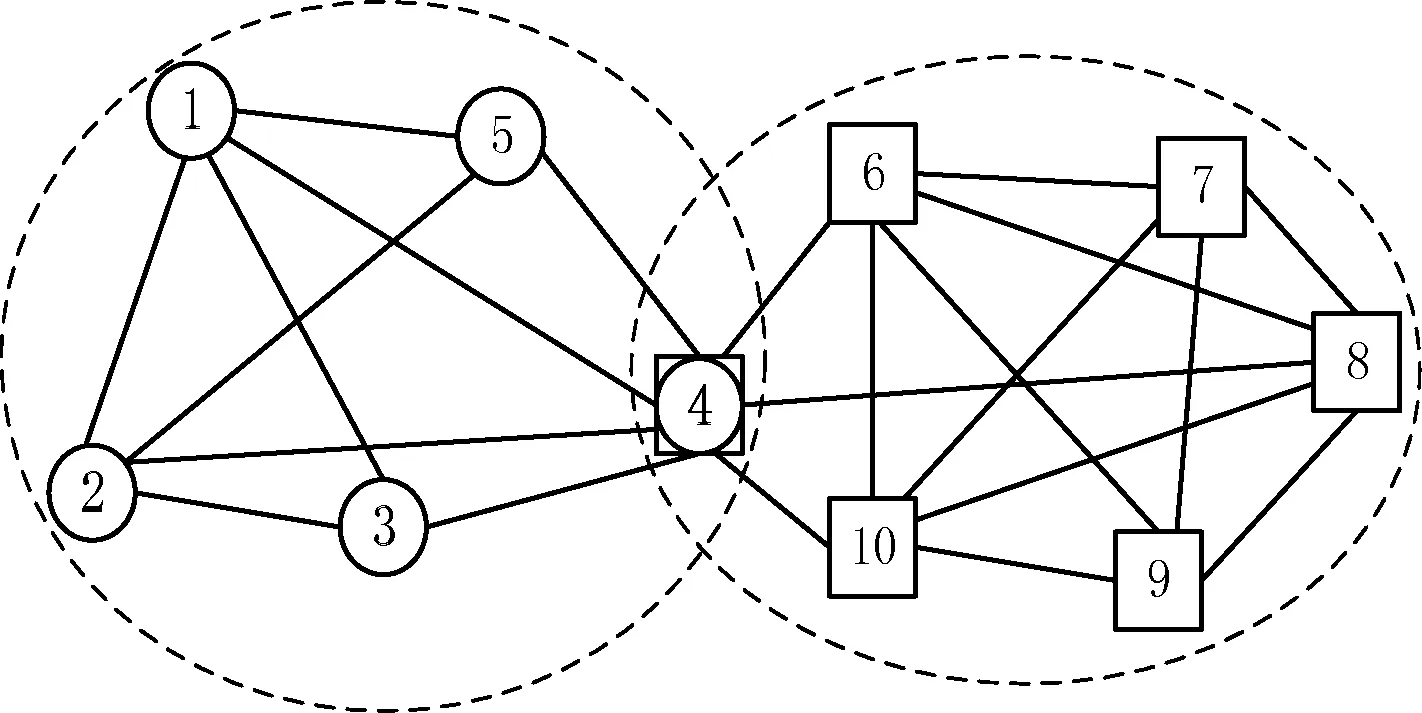
图1 重叠社区
本文提出一种改进的重叠社区发现算法(L-SLPA),其扩展了SLPA,在算法的初始阶段先对网络进行一次非重叠社区划分,然后给同一社区中的节点分配相同的标签,而不是像SLPA一样给所有的节点分配不同的标签。标签分配完成后,仅对边界节点执行Speaker-Listener标签传递的迭代过程,最后对各节点包含的所有标签进行过滤。
1 相关工作
1.1 重叠社区发现算法
重叠社区结构更加贴合现实网络的实际情况,这一理论和实践上的重要意义促使世界上很多研究人员对复杂网络的社区进行研究,很多有效的模型被不断提出。派系过滤算法(CPM)基于这样的假设:一个社区由重叠的完全连接的子图集组成,并通过搜索相邻的团来检测社区[3],它适用于密集连接的网络中,对于稀疏的网络算法效率将会变得很低。Raghavan等[4]提出了一种简单的标签传播算法(Label Propagation Algorithms),每个节点都用一个唯一的标签初始化,并且在每一步中,每个节点都采用它的大多数邻居当前拥有的标签。该算法时间复杂度低、简单、实用性强、效果好。Gregory等[5]基于LPA引入了社区从属系数,提出具备重叠社区发现能力的COPRA,但是该算法并没有解决标签传播所带来的随机性问题。Lancichinetti等[6]定义了一个可以衡量节点紧密连接程度的fitness函数,LFM算法随机选择一个没有被分配社区的节点作为种子,通过优化fitness函数以形成一个社区,但是LFM算法较高的时间复杂度使得其在大型网络中的效率并不理想。
1.2 Louvain算法
Blondel等[7]提出的基于启发式和模块度Q优化的Louvain算法,是一种近线性运行时间的贪婪算法。该算法对多层次的图进行操作,在每个层次上应用顶点移动程序(VM)来提高模块性,具有运行速度快、效果稳定等优点。
(1)
(2)
式中:Aij为节点i和节点j之间边的权值;ki为与顶点i相连的边的权值和;ci为顶点i所在的社区;m为图中所有边的数量的1/2;如果u=v则δ(u,v)为1,反之为0;∑in为社区c中所有边的权重和;∑tot为社区c中节点关联的所有边的权值和;ki,in为顶点与社区c中节点所有相连边的权重和。
1.3 SLPA
SLPA(Speaker-ListenerLabel Propagation Algorithms)是一种基于一般说话者和收听者的信息传播过程的算法。SLPA在LPA的基础上引入了Speaker(标签传播节点)和Listener(标签接受节点)两个概念[8],如图2所示。它根据成对的交互规则在节点之间传播标签。当一个节点忘记了在前一个迭代中获得的知识时,SLPA为每个节点提供一个大小为T的内存来存储接收到的信息(即标签)。节点内存中观察到标签的概率被解释为成员强度。SLPA不需要提前指定社区数量,时间复杂度为O(Tm),与边数m呈线性关系,其中T为预定义的最大迭代次数(如T≥20)。SLPA还可以通过一般化交互规则(SLPAw)来适应加权和定向网络。
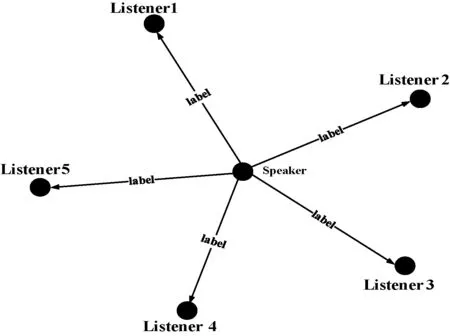
图2 SLPA中的Speaker和Listener
SLPA的大致步骤如下:
(1) 初始化每个节点,给每个节点一个唯一的标签。
(2) 随机挑选一个节点作为Listener,其邻居节点为Speaker。
(3) Speaker以各个标签在其内存所有标签中存在概率随机发送一个标签,Listener接收所有发送过来的标签中最多的那个标签。
(4) 统计每个节点各类标签数量,将个数超过要求的标签作为节点最终的社团标签。
但是由于SLPA在初始化过程中,为每个节点都分配了一个唯一的标签,对于复杂网络而言,标签的分配和传播会消耗大量的资源。而且标签的传播过程中的随机选择策略会造成SLPA的不稳定性和随机性。
2 基于SLPA优化的社区发现算法
在SLPA的初始阶段,每个节点都被分配了一个单独的标签,当网络规模较大时,这无疑消耗了巨大的资源。所以,可以先对复杂的网络进行一次初步的划分,然后给相似的一类节点分配一个相同的标签,这样能够大大减少标签分配的资源消耗。同时,重叠节点通常处于社区的边缘,因此,本文在改进的算法中引入了边界节点的概念(定义3)。在T次迭代中,只需要对边界节点进行Speaker-Listener的标签传递过程,而不是对所有的节点都进行标签传递,从而提高算法的效率。最后根据阈值r,过滤每个节点中的无效标签(定义4),保留下来的标签所对应的社区即为该节点归属的社区。
定义1一个复杂网络可以表示为G=(V,E),E为所有边的集合。
定义2假设网络G划分得到的社区集为C={c1,c2,…,cn},ci表示划分得到的第i个社区。
定义3对于G=(V,E)的社区划分C={c1,c2,…,cn},若vi∈ci,vj∈cj,i≠j,并且∀eij∈E(eij为两节点间的边),则称vi和vj为边界节点。
定义4当某类标签li出现的概率P(li)小于阈值r,则将该标签称为无效标签,具体条件表示为:
(3)
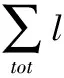
本文将改进后的算法称为L-SLPA,算法的具体步骤如算法1所示。其中步骤1-步骤3为非重叠社区划分阶段,步骤4-步骤5为标签分配和边界节点统计阶段,步骤6-步骤9为Speaker-Listener标签传递的迭代阶段。
算法1L-SLPA
输入:复杂网络G(V,E)。
输出:重叠社区{c1,c2,…,cn}。
步骤1初始化所有节点,每个节点为一个单独的社区。
步骤2每个节点分别加入邻居社区中,按式(2)计算模块度增益ΔQ。假如存在ΔQ大于零,则将该节点加入ΔQ最大的社区中。
步骤3将社区合并成超点,重复步骤1和步骤2,直到模块度Q不再变化。
步骤4为同社区中的节点分配一个相同的标签,不同社区中的节点分配到的标签不同。
步骤5统计边界节点。
步骤6在边界节点中随机挑选一个节点作为Listener,其邻居节点为Speaker。
步骤7Speaker以各个标签在其内存所有标签中存在概率随机发送一个标签,Listener接收所有发送过来的标签中最多的那个标签。
步骤8重复步骤6和步骤7,直到达到最大迭代次数T。
步骤9统计每个节点各类标签的数量,根据阈值r,过滤无效标签,将剩下的标签作为节点最终的社团标签。
假设有这样一个图,其中包含7个节点和11条边。先对其进行非重叠社区发现,节点1-节点3被划分为社区1,节点4-节点7被划分为社区2。给社区1中的所有节点分配一个标签1,给社区2中的所有节点分配一个标签2。同时,图中的节点1、节点3、节点4和节点7为边界节点,对这4个边界节点执行Speaker-Listener的标签传递过程。算法结束后,发现节点1同时包含着标签1和标签2,则可以认为,节点1同时归属于两个社区,是一个重叠节点,如图3所示。

图3 L-SLPA举例
当复杂网络的规模不断增大,时间复杂度是算法需要考虑的一个重要问题。在本文算法的第一阶段,非重叠社区发现的时间复杂度为O(m),其中m为复杂网络中边的数量。第二阶段中,统计边界节点的时间复杂度为O(m),SLPA的整个标签传递过程的时间复杂度为O(Tn),其中:T为算法的迭代次数;n为节点的数量。所以,L-SLPA整体的时间复杂度为O(m+Tn),基本与网络中边的数量呈线性关系。
3 实 验
本文将L-SLPA与几种具有代表性的重叠社区发现算法进行对比,分别为SLPA、Copra[5](另一种标签传播算法)、CPM算法[3](派系过滤算法)和LFM算法[6](一种基于适应度函数的社区扩展算法),以验证L-SLPA的性能。本文实验所有算法均采用Python实现,运行环境为PC,基本配置:CPU为3.1 GHz Intel Core i5,内存为8 GB。
3.1 实验数据集
本文选取了6个规模不同的真实网络数据集[9-17],对改进的L-SLPA及4种对比的重叠社区发现算法进行测试。真实网络数据集的具体参数如表1所示。
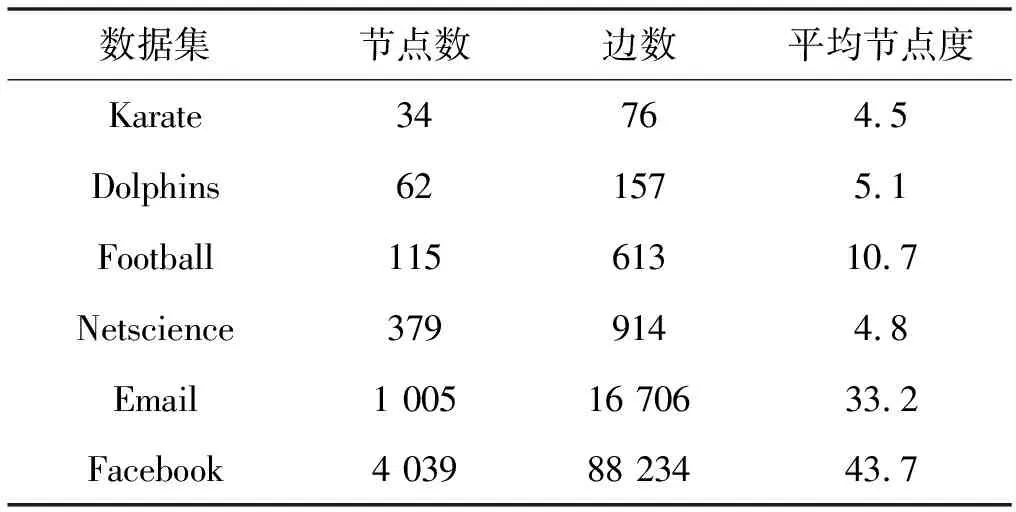
表1 真实网络数据集
Lancichinetti 等[18]提出的LFR基准网络被广泛应用于复杂网络分析中,通过调整参数生成规模不同的人工合成数据集。本文实验中的基准测试网络参数设置如表2所示,其中:节点的数量N分别被设为1 000和5 000;节点的平均度k被设为10;最大的节点度kmax为50;混合参数μ控制着网络中潜在的社区结构,μ越大社区结构越模糊,μ被设置为0.1和0.3;社区的规模设定为10~50之间;重叠节点数量on为总节点数的10%;每个节点归属的社区数om则为2~8。
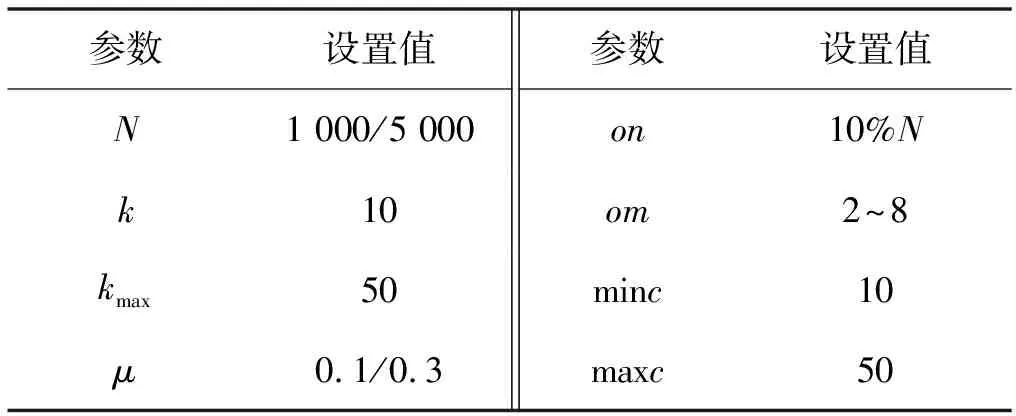
表2 LFR基准网络参数
3.2 评价指标
3.2.1重叠模块度QE
模块度Q是由Newman提出,用于评价社区划分结果的好坏,但是该函数仅适用于非重叠社区划分的结果。为了能够合理地评价重叠社区发现的结果,Chen等[19]在模块度函数的基础上提出了重叠社区的模块度指标QE,QE的值在0到1之间,值越高代表社区划分得越准确。
(4)
式中:m为图中边的总数;A为网络的邻接矩阵,若节点i和节点j之间存在一条边,则Aij=1,反之为0;ki、kj分别为节点i和节点j的度;oi、oj为节点i和j所属的社区数。
3.2.2标准互信息NMI
模块度能够对社团划分结果好坏进行评价。如果知道网络的真实社区划分情况,则可以通过得到的社区划分结果与真实的社区划分情况进行对比,这样就能测算出社区发现算法的准确性。NMI(标准化互信息)[6],评价一个社区划分和标准划分结果之间差异性的指标,通常被用来评价一个社区发现算法的准确性。NMI的值在0到1之间,值越高代表社区划分得越准确。
(5)
式中:X和Y分别代表真实的社区结构和社区发现算法得到的社区结构;H(X|Y)norm和H(Y|X)norm为社区分布的条件信息熵。
3.3 算法参数选取
L-SLPA最终的结果依赖于阈值r和T的选取。其中r的取值范围为0~1,如果阈值r取值过小,很多节点会被错误地划分为重叠节点,影响重叠划分结果的准确性,但是当阈值r的取值接近1时,又会使该算法退化成非重叠社区发现算法。本文在N=1 000的人工数据集上测试选取不同阈值r时算法结果的收敛情况,根据图4可以发现,当r大于0.04时,算法检测到的社区数量和真实社区数量之比趋于稳定。所以,本文在后续的实验中取r的值为0.05。
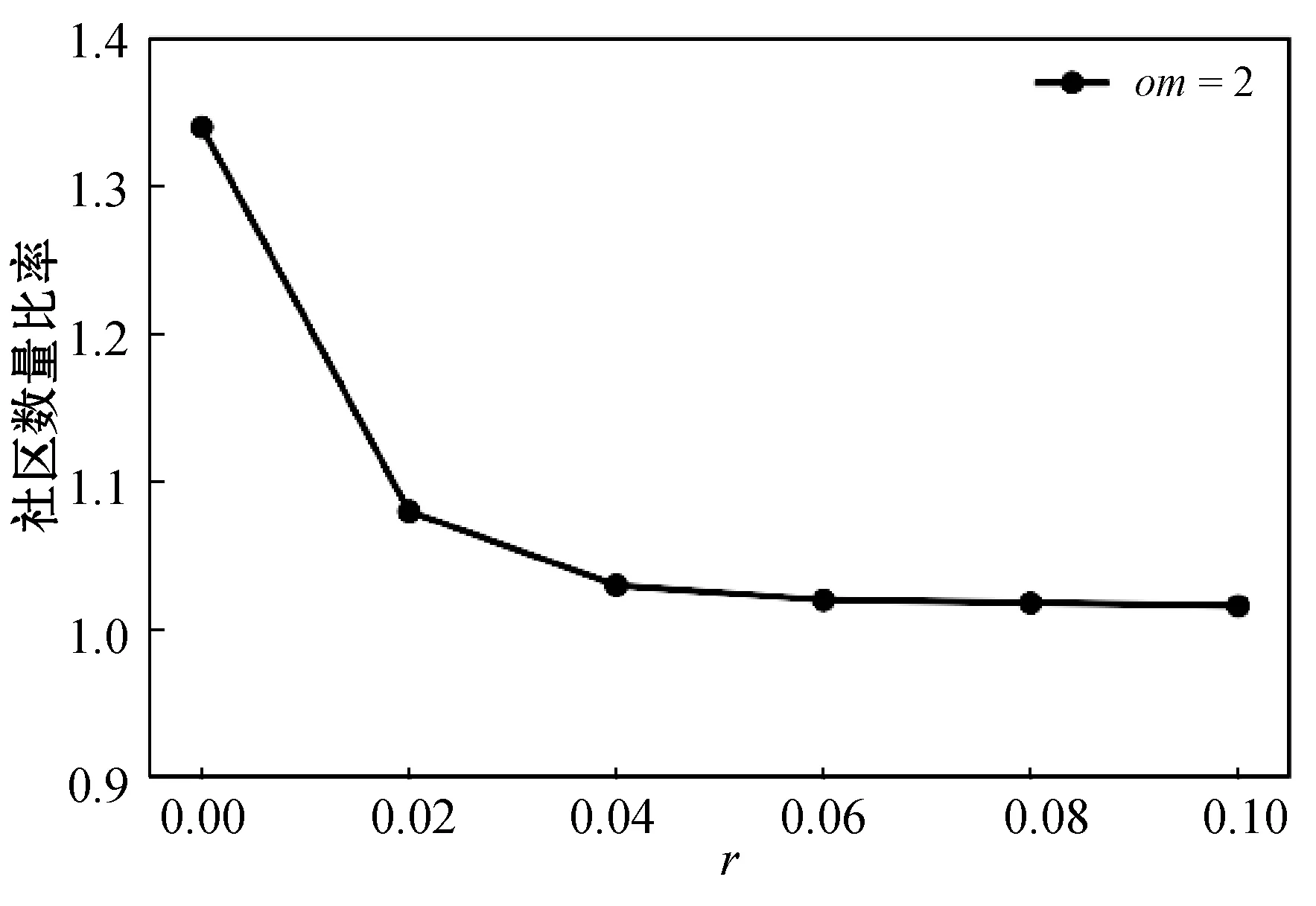
图4 阈值r的收敛表现
根据图5可以发现,随着算法的最大迭代次数T取值的增大,算法的准确性会有增长的趋势,但是过多的迭代次数会降低算法的运行速度。因为T大于20后,更多的迭代次数并没有给算法结果带来很大的提升,所以在本文中,选取T的值为20。

图5 迭代次数T的收敛表现
3.4 实验结果
本文首先在6个规模不同的真实网络数据集上对算法的性能和效果进行对比验证,这些对比算法的参数设置如下:对于Copra,v被设置为1到10不等,取值间隔为1;对于CPM算法,k被设置为2到8不等,取值间隔为1;对于LFM算法,设置α的值为1.0;对于SLPA和L-SLPA,将迭代次数T设置为20,过滤参数r被设置为0.05。实验结果选取各参数下得到的最大值进行对比。
本文实验将5种算法在规模不同的真实网络上各运行100次,对得到的运行时间取均值,最终的结果如图6所示。可以发现,当网络的节点数较少时,除SLPA外,其余4种算法的时间开销相当。但是随着网络规模的不断增大,4种对比算法的运行时间明显增加。L-SLPA的运行时间仍然呈现线性增长,并且远低于其他4种算法的运行时间,效率更高,可扩展性更好。
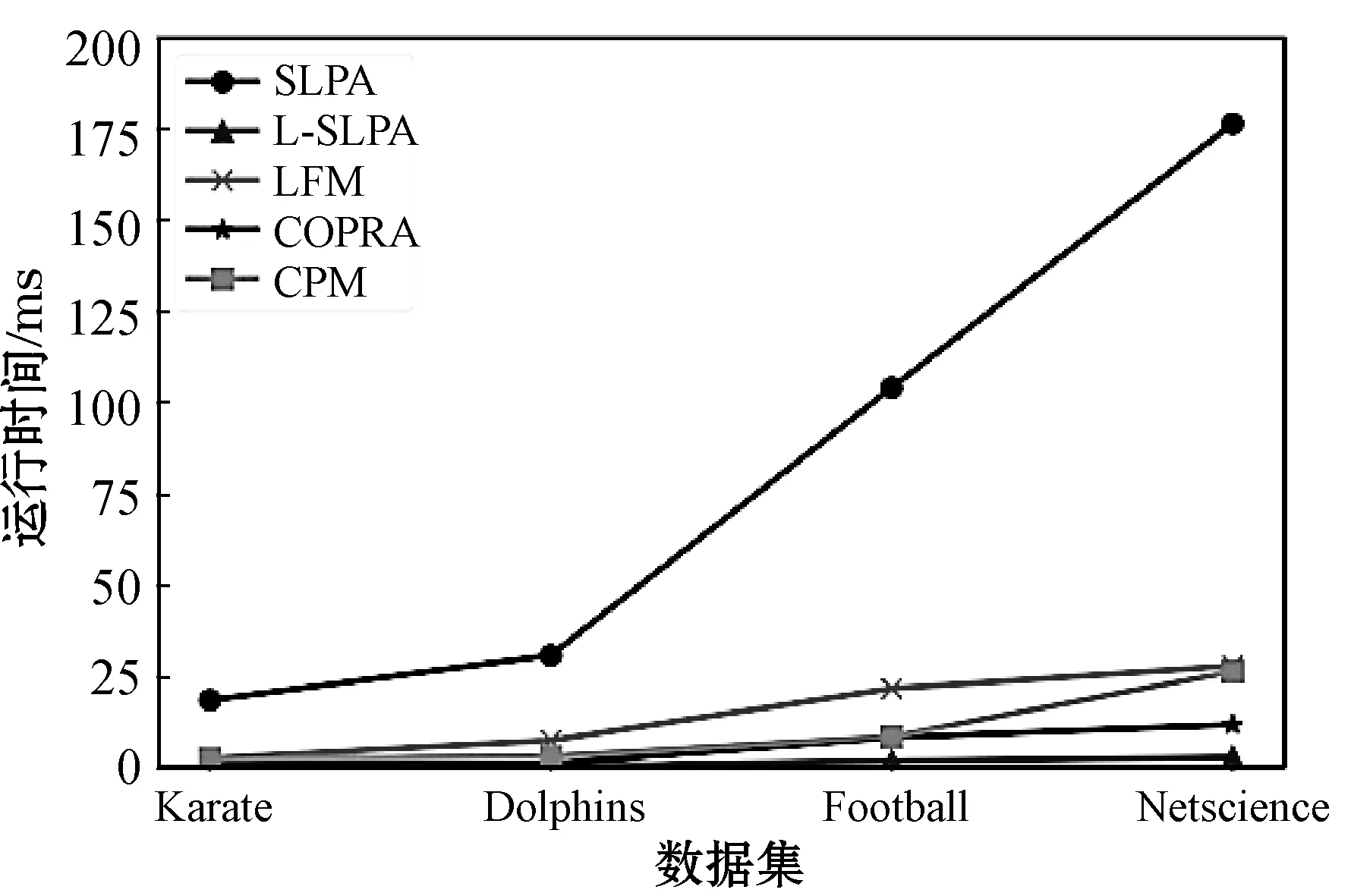
(a)
同样地,采用上述参数设置,将5种算法分别在每个数据集上运行10次,对得到的重叠模块度QE取平均值,最终的结果如图7所示。总体来看,当网络规模较小时,Copra的划分结果的重叠模块度最高,但是随着节点数量增加,划分结果明显有所下降。而L-SLPA在各网络上的划分结果都具有较高的重叠模块度QE,SLPA次之。结果表明,L-SLPA能够在不同规模的网络中发现较高质量的重叠社区。
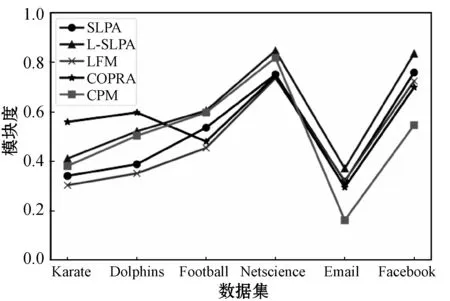
图7 真实网络划分结果的重叠模块度QE
为了测试L-SLPA是否能够有效地降低标签传递策略所引起的随机性问题,使用SLPA和L-SLPA分别在N=1 000和N=5 000的LFR基准测试网络上进行了100次社区发现,每次划分得到的社区数量如图8所示。可以发现,SLPA得到的社区数量随机性较大,结果并不稳定。在N=1 000的LFR基准测试网络上,得到的社区数量在65~95个之间波动;在N=5 000的LFR基准测试网络上,得到的社区数量在352~396个之间波动。相同情况下,L-SLPA得到的社区数量波动较小,结果比较稳定。

图8 LFR基准测试网络上划分的社区数量
最后,生成了4组不同参数的LFR基准测试数据集,结合式(5),对SLPA和L-SLPA进行了性能对比。将两种算法分别在每个数据集上运行10次,对得到的NMI值取平均值,最终结果如图9所示。

图9 LFR基准测试网络实验结果
总体上,随着每个节点归属的社区数om和混合参数μ的增加,两种算法的社区发现结果均有所下降。在N=1 000的LFR基准测试网络中,L-SLPA的划分结果和SLPA的划分结果大致相等。然而随着网络规模的变大,当N=5 000时,相较于SLPA,L-SLPA的性能下降比较多。这是由于L-SLPA的第一阶段执行了一次基于模块度Q优化的非重叠社区划分,而随着网络规模不断增大,基于模块度Q优化的方法的解析度问题便会逐渐凸显出来,算法得到的社区数量有可能远小于真实的社区数量,这会导致NMI值的下降。虽然此方法发现的社区数量小于实际情况,但是划分得到的社区结构稳定,与实际情况吻合度较高,所以并不会影响社区发现结果的模块度。
4 结 语
由于标签传递策略的随机性,SLPA的社区发现结果并不够稳定。同时,SLPA初始的标签分配需要消耗大量的资源。为了解决SLPA的这些缺点,本文基于SLPA提出一种更加高效的重叠社区发现算法,在算法的初始阶段,基于模块度Q优化对网络进行一次非重叠社区划分,对同社区的节点分配一个相同的标签后再对边界节点执行Speaker-Listener标签传播的迭代步骤。实验结果表明,相较于其他重叠社区发现算法,L-SLPA运行速度快,具有更好的可扩展性,在降低了标签传播算法结果的随机性的同时保证了结果的准确性。
