基于小波变换和改进的Retniex雾天图像增强
2021-01-15张振华陆金桂
张振华 陆金桂
(南京工业大学机械动力与工程学院 江苏 南京 211816)
0 引 言
计算机视觉科学技术在日常生活中的重要性与日俱增,而户外采集图像系统(例如摄像机、公共安全监控、道路监控等)极易受雾霾恶劣天气影响,导致采集的图像对比度低、可读性差,无法满足要求。近年来,由于尾气过量排放、森林砍伐、环境污染等原因,雾霾天等恶劣天气越来越频繁发生,户外采集系统所采集图像的视觉效果难以令人满意,因此对雾天图像增强的研究有着重要意义[1-2]。
图像增强最常用的方法有线性拉伸[3-4]、HE法[5]、同态滤波[6]和反锐化掩膜法[7]等。以上方法在增强图像时,都存在着过度增强噪声的缺点。小波分析因具有多分辨率分析能力[8-9],可以将噪声与信号进行初步分离,许多学者将其应用于雾天图像的增强。文献[10]提出了一种小波变换和CLAHE结合的雾天图像增强算法。文献[11]提出了一种结合小波变换和HE法的雾天图像增强算法。文献[12]提出了一种基于小波变换和非线性变换的雾天图像增强算法。文献[13]提出了一种结合小波变换和阈值函数的雾天图像增强方法。Kim等[14]提出了一种小波变换结合暗通道先验的雾天图像增强算法。Yang等[15]提出了一种小波变换结合软阈值去噪的图像增强方法。Kansal等[16]提出了一种小波变换结合阈值分割技术的雾天图像增强算法。He等[17]提出了一种基于小波变换和正则化优化的雾天图像增强算法。上述基于小波变换的雾天图像增强方法都难以在增强图像细节和抑制雾霾噪声之间取得平衡,会出现过度放大噪声或者损失图像细节的问题。
Retinex理论[18-19]是在20世纪70年代被提出的,其假设一幅图像可以用目标反射函数和环境亮度函数的乘积表示,改变两者在原图中的比重,就可以抑制噪声增强图像细节[20]。文献[21-22]将其应用于图像增强中。
本文提出了一种基于小波变换和改进的Retniex的雾天图像增强算法,可以有效地增强雾天图像并且消除雾霾噪声。首先,它利用小波变换良好的多分辨率分析能力,将原始图像分解为低频子带图和高频子带图;其次,使用双边滤波改进传统的单尺度Retinex算法,解决其局部细节丢失的缺点,使用改进的Retinex算法处理低频子带图,去除雾霾噪声;然后,使用模糊规则增强算法,结合高频子带图局部特性设计不同的增强系数对其进行增强;最后,进行小波逆变换,得到最终结果。
1 算法设计
1.1 小波变换
在天气良好条件下,空气中粒子成分主要是大气组成分子(氧气、氮气、二氧化碳等)和微粒(悬浮固体颗粒、小水滴等)。这种条件下,大气中分子和微粒反射、散射、吸收太阳光的能力较弱,户外图像采集系统可以获得充足光亮,捕捉到的像质清晰,视觉效果较好。而在雾霾恶劣天气下,空气中微粒半径较大,半径较大的微粒对太阳光的反射、散射吸收能力较强,户外图像采集系统无法获得充足光亮,最终导致图像细节模糊不清,成像较差。所以雾霾天气条件下,大气混浊,光线衰减程度大,导致视野混浊,远处景物模糊不清。
基于小波变换的雾天图像增强方法,使用小波变换的多分辨分析能力,将雾天图像分解为低频子带图和高频子带图,然后根据其特点对不同的部分设计不同的处理方法。低频部分包含了雾天图像的大部分噪声,高频部分对应图像的细节部分。
二维图像经小波分解可以分解为4个子图像:
Lif(x,y)=
(1)
(2)
(3)
(4)
图1是小波分解示意图,小波重构按相反过程进行。其中:LL1表示原图的低频子带图,保持了原图的主要信息,集中了原图像的绝大部分的噪声;HL1为水平方向边缘信息的子带图;LH1为垂直方向边缘信息的高频子带图;HH1为对角线方向综合信息的高频子带图。高频子带图反映了图像的细节信息,如何增强高频子带图是图像增强的关键问题。对LL1再次分解即可得到LL2、HL2、LH2、HH2四个子图像[23-24]。

图1 雾天图像的二层小波变换分解图
1.2 基于改进Retinex的低频子带图增强
在对雾天图像的处理中,Retinex算法可以将照射分量从原始图像中分离出来,然后将其去除,即可得到表示细节信息的反射分量。但Retinex算法是对图像整体处理,缺乏针对性,无法较好地去除图像中的雾霾噪声。
Retinex理论认为,一幅图像可以由照射分量和反射分量乘积表示,其数学表达式为:
I(x,y)=L(x,y)·R(x,y)
(5)
式中:I(x,y)为输入的图像;L(x,y)为照射分量;R(x,y)为反射分量。为了消除照射分量的影响,恢复真实场景,对式(5)的两边取对数得:
lgI(x,y)=lgL(x,y)+lgR(x,y)
(6)
为了估算出照射分量,使用高斯滤波和原图进行卷积运算,最终得到单尺度的Retinex算法公式:
R′(x,y)=lgI(x,y)-lg[F(x,y)*I(x,y)]
(7)
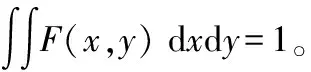
传统的单尺度Retinex算法中的高斯滤波器在滤波计算过程中仅考虑各像素点的距离信息,即认为在窗口邻域内,离中心点近的点其权重系数大,反之则权重系数小。
这种仅考虑距离的计算方法,在像素灰度值没有明显变化的平坦区域是可行的,但若在边缘区域,像素的灰度值存在跃变,中心点两侧的像素灰度值会有显著差异,该计算方法会损失图像边缘信息。
除了空间距离因素,各像素灰度值的差异也是双边滤波器在滤波过程中参考的重要因素,即灰度因子。在滤波计算的窗口内,和中心点灰度值差异越小的点权重越大,反之越小,这种计算方法更为合理,图像边缘信息得以保护。
实验证明:使用双边滤波的Retinex算法对图像进行增强,可以避免损失图像边缘细节信息,得到令人满意的增强效果。
双边滤波对输入图像照射分量的估计如下:
(8)
λ[(x,y),(x′,y′)]=λs[(x,y),(x′,y′)]·
λr[(x,y),(x′,y′)]
(9)
(10)
(11)

实验中发现,如果将图像中的照射分量完全去除,增强后的图像会显得不自然,因此在去除照射分量的计算过程中,引入权值α(0<α<1),其表达式如下:
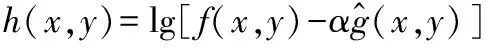
(12)

低频子带图增强过程如下:
1) 因单尺度Retinex算法的输入必须是灰度图,故将有正有负的低频子带图系数全部转换到0~255范围:
(13)
式中:Imin和Imax代表系数的最大值和最小值;I′(i,j)为映射后结果。
2) 将I′(i,j)作为输入,根据式(12)进行增强。
3) 将处理后的低频子带图系数映射回(Imin,Imax)范围内。
1.3 高频子带图增强
雾天图像经小波分解后的高频分量对应图像的细节信息,传统的全局增强算法如HE算法,线性对比度拉升,在对图像进行增强时,容易出现放大噪声、图像过度增强问题。因此本文根据模糊规则和高频子带图中像素点的局部特性计算其增强系数,针对图像中的局部信息的特点,进行不同程度的增强。具体步骤如下:
1) 计算高频子带图局部对比度,窗口大小为3×3,公式如下:
(14)
式中:D(i,j)表示子带图的局部对比度;Imax为窗口内最大灰度值;Imin为窗口内最小灰度值。
2) 计算隶属度ηt(t=1,2,3)(η1为低细节区域隶属度,η2为中细节区域隶属度,η3为高细节区域隶属度)。
局部对比度D(i,j)在图像的平坦区域和细节区域会有不同,比如在像素灰度值没有显著变化的平坦区域,D(i,j)的值比较小。在像素灰度值出现跃变的细节区域,D(i,j)的值比较大。低、中、高细节区域无法精确划分,所以根据每个像素的局部对比度的大小来计算其每一种隶属度的大小,具体计算公式如下:
ηt(i,j)=4sigm{as[D(i,j)-bs]}×
sigm{-as[D(i,j)-bs]}
s=1,2,3D(i,j)∈[0,1]
(15)
式中:sigm(x)=1/[1+exp(-x)]。式(15)中的参数可通过实验和经验确定:a1=a3=20,a2=30,b1=0,b2=0.8,b3=1。
3) 计算增强系数。实验结果表明,对中细节区域进行重点增强处理,图像视觉效果最佳。设低、中、高区域的增强因子分为λlow、λmid、λhigh。将第2步中计算得到的隶属度作为权值,计算各点的最终增强系数,公式如下:
(16)
实验发现:取λlow=λhigh=1.5、λmid=3时,可以对图像达到理想增强效果。
4) 对高频子带图进行增强:
f′(i,j)=λ[η(i,j)]×f(i,j)
(17)
式中:f′(i,j)表示增强后小波系数;f(i,j)表示原始小波系数。
1.4 算法流程
1) 使用sym4小波将雾天图像分解为低频和高频两部分;2) 使用改进的Retinex算法对低频子带图进行去噪增强;3) 根据高频子带图的局部特性,设计合适的增强系数进行增强;4) 将处理后的两部分进行小波逆变换,得到增强后的雾天图像。
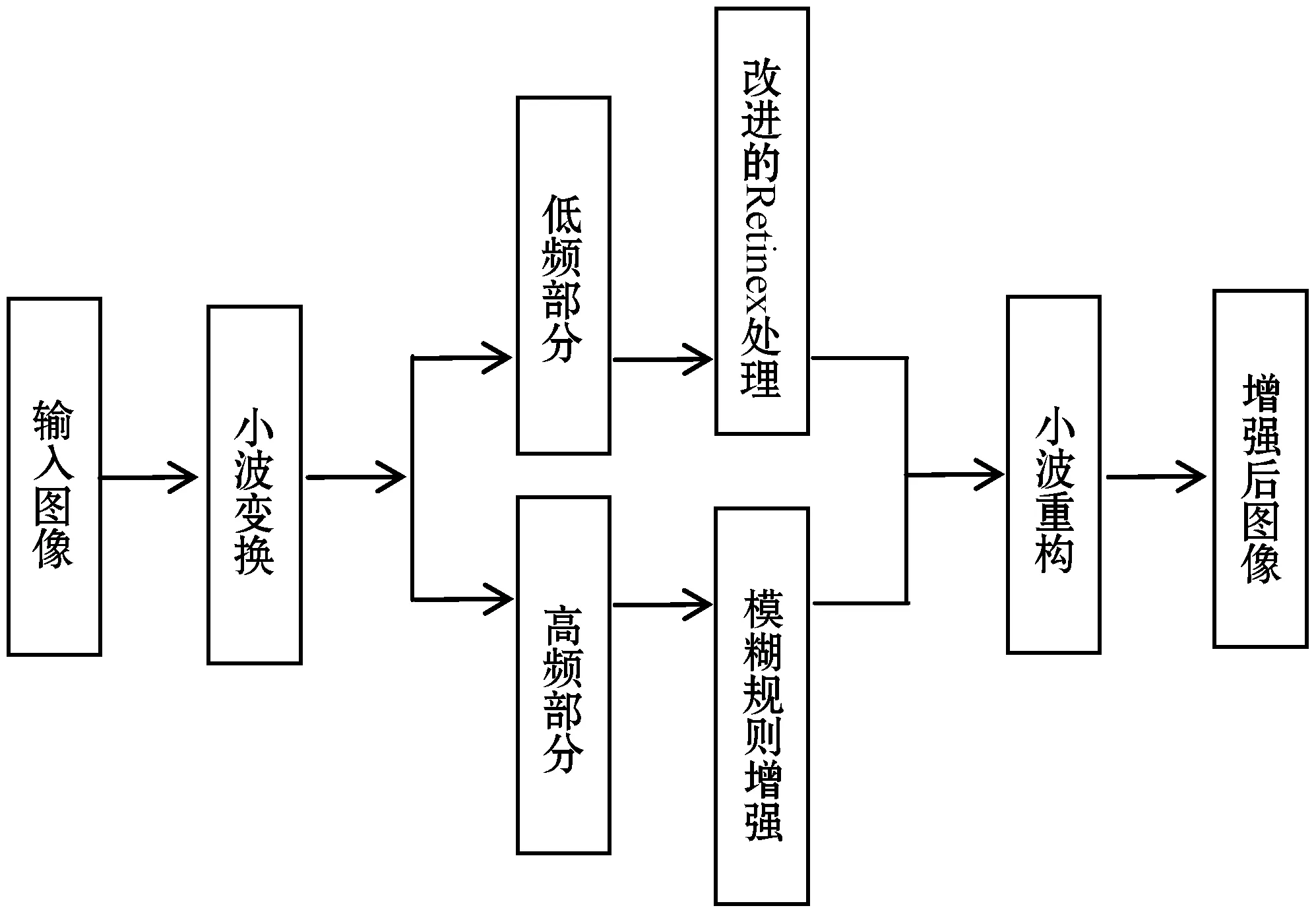
图2 算法流程图
2 实 验
本文的实验平台为英特尔奔腾@3.50 GHz处理器,内存8.00 GB,Windows 10操作系统,算法使用MATLAB 2016a编写。为验证本文算法,选取不同类型场景、不同景深、不同视野范围的200幅图片作为实验数据库。
所有雾天图像分别使用HE算法、小波结合HE算法、改进的Retinex算法和本文方法进行处理并比较分析。
本文算法实验参数:小波基选择sym4小波;改进的Retinex:卷积窗口大小5×5,σs=65,σr=15,α=0.5;模糊规则增强:a1=a3=20,a2=30,b1=0,b2=0.8,b3=1。λlow=λhigh=1.5,λmid=3。
为了便于直观理解,现从实验数据库中选择三组代表性的图片进行展示,如图3所示,(a)、(b)、(c)分别为场景复杂多目标物的某小区道路监控图像、景深开阔大视野的城市郊区图像、单一目标物小视野的某建筑物外观图。各算法对雾天图像的处理结果如图4-图7所示。

(a) (b) (c)图3 原始图像

(a) (b) (c)图4 HE算法对雾天图像处理结果

(a) (b) (c)图5 小波+HE算法对雾天图像处理结果

(a) (b) (c)图6 改进的Retinex算法对雾天图像处理结果

(a) (b) (c)图7 本文算法对雾天图像处理结果
从视觉效果看,HE算法处理的图像虽然抑制了一部分雾霾噪声(图4(b)),改善了图像的对比度,比如图中远处的道路、河流变得清晰,但是图像局部细节消失,近处的花草树木基本消失,淹没在阴影里,图像视觉效果较差。小波结合HE算法一定程度上去除了图像中的雾霾噪声(图5(b)),图中景物变得略微清晰均匀,但是图像细节没有得到有效增强,整体上看并不清晰,图像可读性不能令人满意。改进的Retinex方法在去除噪声方面取得了一定的效果(图6(b)),景物轮廓显现出来,但是图像整体偏白,图像对比度没有得到改善,整体视觉效果一般。采用本文提出的方法处理的图像雾霾噪声去除效果明显(图7(b)),图像细节显著增强,图中的道路、树木轮廓变得立体清晰,视觉效果良好。
为了客观评价算法性能,现选择信息熵作为客观指标。信息熵表示图像包含的平均信息量(见表1),对雾天图像的增强中,其值越大,表明图像内容丰富,对图像噪声的去除效果好,图像质量好。其表达式为:
(18)

表1 经不同算法增强之后的图片的信息熵
可以看出,4种算法对雾天图像的增强有不同程度的效果。与其他3种方法相比,图像经本文方法处理后,信息熵提升效果最佳,说明处理后的图像细节信息丰富,图像去噪效果好,图像细节得到了较大增强。由此可见,本文方法对雾天图像的增强效果较为理想。
3 结 语
针对现有基于小波变换的雾天图像增强算法在抑制噪声和增强图像细节两者之间无法取得令人满意的结果,本文提出了一种结合小波变换和改进的Retinex的雾天增强方法。
1) 使用sym4小波分解雾天图像,得到低频子带图和高频子带图,对高频子带图和低频子带图设计针对性算法分别处理,最后进行小波重构,得到增强图像。
2) 为了更好地处理低频子带图,本文对传统的Retinex算法进行改进,用具有边缘保护性的双边滤波替代高斯滤波估计低频子带图的照射分量,解决了传统的Retinex算法容易导致图像边缘细节模糊的缺点;用改进的Retinex的算法对低频部分进行处理。针对高频部分,传统的全局增强算法容易放大噪声、过增强问题,而本文根据图像局部特性,设计不同的增强系数以达到最优的增强效果。
实验表明,本文算法不仅有效增强了雾天图像细节信息,而且抑制了图像中的雾霾噪声,在去噪和增强细节之间取得了较好的平衡,综合效果优于对比算法。
