中长波双色碲镉汞红外探测器器件模拟与分析

吴亮亮,高 达,刘 铭,王 丛,王经纬,周立庆

(华北光电技术研究所,北京 100015)

1 引 言

碲镉汞(HgCdTe,MCT)材料因其组分可调、直接带隙和高量子效率等特点,可实现短波、中波和长波三个“大气透明窗口”红外波段的高性能探测,所以在夜视和引擎探测等军事领域及温度和热探测等民用领域具有重要应用价值[1-3]。

随着红外探测器的不断发展,红外隐身技术也在不断提高,通过使在特定波段上目标与环境背景具有相似的发射率,从而导致红外目标对比度的下降,难以识别。由于地球大气有短波(1～2.5 μm)、中波(3～5 μm)和长波(8～12 μm)三个红外辐射窗口,若一个热成像系统能在多波段对目标和环境的辐射特征进行同时探测,通过对比不同辐射波长下的辐射特征,就可以对复杂的背景进行抑制,实现红外探测不受环境的制约,准确地提取目标热力学真实温度,提高对目标的探测效果,在目标辨认、信号识别及抗干扰方面的性能由于单色探测器,在军事预警、搜索和跟踪系统中能明显的降低虚警率,以及在地球物理和卫星遥感等方面都具有重要应用价值。

早期双色探测器结构多为镶嵌式,随着探测器技术向更大规模焦平面阵列方向发展,也要求双色器件实现大阵列、焦平面结构以及数字化,而只有叠层式工艺才能实现这一目标,即单个像元能探测两个不同波段,当与先进的多色信息处理算法相结合时,双色红外探测器与单色探测器相比可以进一步提高探测灵敏度。其中,中/长波双色碲镉汞探测器能提供更宽的范围、更远的探测距离,成为双色碲镉汞探测器研究的热点。

双色器件在多层材料结构设计、器件工艺等相对于单色器件更加困难,器件模拟仿真可惊醒器件性能预测,指导材料外延生长,对器件制备具有重要参考意义。本文主要引入非抛物线型的吸收系数模型[4-7],通过模拟器件的光谱响应,分析两个波段(中波MW与长波LW)之间的光谱串音以及吸收层和短波阻挡层对器件响应率及串音的影响[8-10]。

本文采用的是加拿大Crosslight公司的APSYS软件进行模拟计算分析,该软件能够针对化合物及元素半导体的电、光和热特性作2D/3D有限元分析,涵盖热载流子流体动力学、深能级陷阱其陷阱动力学以及77K低温仿真等多种物理模型,同时它具有大量的材料程序库以及业界领先的数值收敛性,使得它便于模拟探测器及LED等半导体感光或发光器件。

2 双色器件结构与碲镉汞材料吸收系数模型

目前国际上有多种研究机构的多种器件结构,其中法国Sofradir公司的准平面结构的工艺路线是基于现有单色平面器件工艺技术的同时探测n-p-P-n-p准平面双色器件结构,其结构如图1所示,器件在77 K下工作,整个像元大小为30 μm,每个像元由两个标准的n-on-p光电二极管组成,两个吸收层由两个不同组分的HgCdTe层组成,两个吸收层之间被短波层隔开,阻止了两个n-on-p二极管间的载流子漂移,降低光谱串音。每个像元上两个二极管的独立电极可以实现同时读出。

图1 准平面双色器件结构Fig.1 Diagram of quasi-planar two-color device structure

从下往上整个器件的各层材料及器件参数(模拟过程中某些材料参数会作为变量)如下:

(1)中波Hg1-xCdxTe层,组分x为0.3,对应截止波长为5 μm,总厚度d为6 μm,空穴浓度p为1×1016cm-3；电极1接触区为n型注入区,注入区深度为1 μm,等效电子浓度n为1×1017cm-3,电极为欧姆接触。

(2)短波Hg1-xCdxTe阻挡层,组分x为0.35,对应截止波长为3.8 μm,厚度d为0.2 μm,空穴浓度p为1×1016cm-3。

(3)长波Hg1-xCdxTe层,组分x为0.225,对应截止波长约为10 μm,总厚度d为8 μm,空穴浓度p为1×1016cm-3；电极2接触区为n型注入区,注入区深度为1 μm,等效电子浓度n为1×1017cm-3,电极为欧姆接触。

(4)电极3为公用电极,接触区域中波Hg1-xCdxTe层厚度为3 μm,电极为欧姆接触。

对于有限元模拟软件而言,在器件模拟分析时首先要考虑的就是网格设定问题,计算你模拟是将整个器件分成很多的小格点,功过计算每个格点位置处的电荷、电势、光照等参数值,最后得出总的器件性能参数值,比如能带、I/V、响应等。如图2所示为模拟设定的网格分布图,设定分为垂直方向和水平方向网格。网格密度设定一般的原则为:在存在突变的界面附近网格点密度加大,其他相同性质的区域网格密度可以相对稀疏；网格间距最大不超过0.1 μm,否则由于网格间隔过大,可能在网格之间存在突变区域,导致运算结果无法收敛,网格间距一般不小于0.001 μm,否则由于网格密度过大,计算时间过长。

图2 器件模拟网格分布示意图Fig.2 Diagram of grid distribution for device simulation

吸收系数是作为探测器材料光电转换效率的一个重要参数。在材料禁带宽度所对应的能量或波长区域,吸收系数将随着光子能量的增加而快速增大,在红外吸收光谱中对应吸收边。一般而言在吸收边附近,吸收系数与光子能量的关系可分为两个部分:在低能区域(带尾效应),吸收系数随着光子能量的减小呈指数衰减；在高能区域(帯间跃迁吸收),吸收系数随着光子能量的增大呈抛物线型关系[3],两者的分界点定义为转变能ET,如图3所示。

图3 中波碲镉汞材料Hg0.7Cd0.3Te的 吸收系数与波长的关系示意图Fig.3 Relationship between absorption coefficient and wavelength of Hg0.7Cd0.3Te

但是对于碲镉汞材料而言,在高能吸收区域,近年来非抛物线型的吸收系数被广泛使用。Moazzami等人[4-5]通过对碲镉汞分子束外延材料吸收系数的测量与拟合,提出了碲镉汞材料的非抛物线型的吸收系数模型,其吸收系数的表达式为:

E=ET:αT

=(-0.020366T2-0.46742T+3878.9)x+

(3.9788T-566.4)

其中,Eg为红外透过谱拟合得出的禁带宽度；ET使得整个吸收系数连续:

Eg=(-0.00091675x+0.00049989)T+

(1.6624x-0.27547)

通过拟合数据,得出一组K和c的经验表达式:

K=57400Eg+67260 ；

c=0.56667Eg+0.0013333

如图3所示为利用上述非抛物线型的吸收系数模型得到的中波碲镉汞材料Hg0.7Cd0.3Te的吸收系数与波长的关系。本模拟将根据上述模型确定不同组分碲镉汞材料的吸收系数α随入射光波长的关系,以表格的形式代入运算中。其他仿真参数如下:

禁带宽度:Eg=-0.302+1.93x-0.81x2+0.832x3+5.35×10-4(1-2x)T

介电常数:εs=20-9.4x

电子有效质量:

电子亲和势:F=4.23-0.813(Eg-0.083)

空穴迁移率:μh=0.01μe

3 模拟计算结果与分析

零偏时和工作电压下中波器件能带图如图4,零偏时和工作电压下长波器件能带图如图5所示。从图4和图5可以看出,当n型碲镉汞材料的掺杂浓度达到3×1017cm-3时,材料进入简并状态,费米能级进入导带之上,这是因为碲镉汞材料的导带能太密度低、电子有效质量小(0.03m0),导致中等n型掺杂浓度就降使得材料进入简并状态。同时,发现对于长波碲镉汞材料,由于禁带很窄,使得耗尽区能带弯曲强烈,载流子隧穿的势垒宽度很窄,直接导致隧穿电流增加,器件暗电流增加。

(a)零偏时

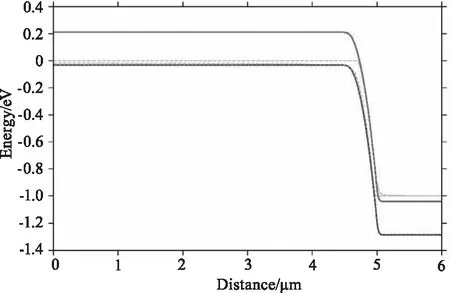
(b)工作电压时 图4 零偏时和工作电压时中波器件能带示意图Fig.4 Schematic diagram of the energy band of the medium- wave infrared device at zero bias and working voltage

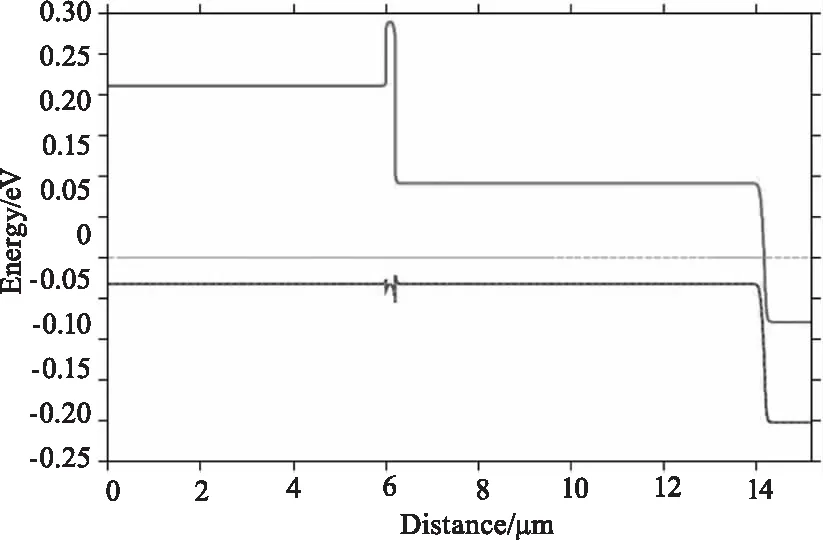
(a)零偏时

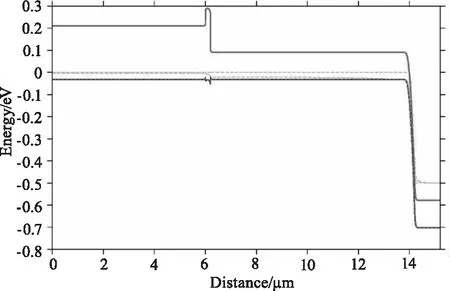
(b)工作电压时 图5 零偏时和工作电压时长波器件能带示意图Fig.5 Schematic diagram of the energy band of the long-wave infrared device at zero bias and working voltage

外置偏压为-1 V时,中波像元电流随波长的关系如图6所示。外置偏压为-0.5 V时,长波像元电流随波长的关系如图7所示。器件所加光装为0.02 W/m2,纵坐标单位为A/m,这是因为器件模拟为二维结构,在未设置几何尺寸的Z方向存在一个未知变量。

如图6所示,中波像元在波长小于5 μm时存在光响应,并且随着波长减小响应减小,这是因为波长越小其吸收系数越大,光的穿透深度越小,产生的光生载流子距离结区较远,很难被电极收集,所以量子效率低。

图6 中波像元电流随波长的关系Fig.6 Medium-wave infrared pixel current as a function of wavelength

如图7所示,长波像元在波长大于4.5 μm时存在光响应,并且随着波长减小响应减小。同时发现存在干涉震荡,这是因为多层材料结构形成干涉。同时发现器件对波长大于10 μm的光存在响应,这是由于吸收带尾效应引起的。

图7 长波像元电流随波长的关系Fig.7 Long-wave infrared pixel current as a function of wavelength

实际器件的光谱响应是光电流部分,如图6和图7所示电流为电极上总的电流,应该减去暗电流,同时单位应该考虑器件为30 μm中心距。如图8所示为归一化之后的光谱响应率曲线。

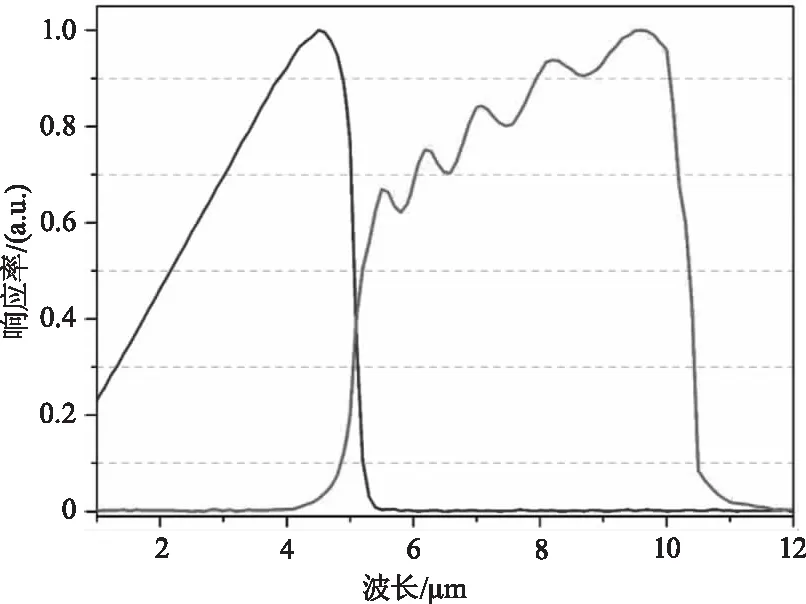
图8 归一化光谱响应曲线Fig.8 Normalized spectral response curve

3.1 中波吸收层厚度对光谱串音的影响

首先研究了器件的中波吸收层厚度对光谱串音的影响,器件结构如图1所示。光谱串音分为中波对长波的串音(MW-LW)和长波对中波的串音(LW-MW),中波对长波的串音为长波像元响应信号中的中波红外光响应占长波红外光响应的比例；长波对中波的串音为中波像元响应信号中的长波红外光响应占中波红外光响应的比例。中波红外与长波红外以5 μm为分界线。如图9所示中波(a)和长波(b)像元的量子效率随中波层厚度变化的关系,如图10所示光谱串音随中波层厚度变化的关系。随着中波层厚度从4 μm增加至8 μm,中波对长波的串音逐渐减小,这是因为中波层厚度增加将中波红外光的吸收,使得长波像元中的中波响应减小,从而使得中波对长波的串音减小。同时随着中波层厚度增加,长波对中波的串音线性增大,这是因为随着中波层厚度增加,其厚度超过波长较短的红外光的透射深度与少子扩散长度之后,导致光生载流子被电路收集的数量减小,所以最终串音增大。同时考虑中波对长波的串音、长波对中波的串音,最终器件选择中波层厚度为6 μm。

图9 中波和长波像元的量子效率随中波层厚度变化的关系Fig.9 The relationship between the quantum efficiency of medium-wave

图10 光谱串音随中波层厚度变化的关系Fig.10 The relationship between spectral crosstalk and the thickness of medium-wave layer

3.2 阻挡层组分对光谱串音的影响

其次研究了器件的阻挡层组分对光谱串音的影响,器件结构如图1所示。如图11所示中波(a)和长波(b)像元的量子效率随阻挡层组分变化的关系,阻挡层厚度为0.2μm。如图11所示阻挡层组分增加不影响中波像元的光谱响应,长波对中波的串音为2.08 %。

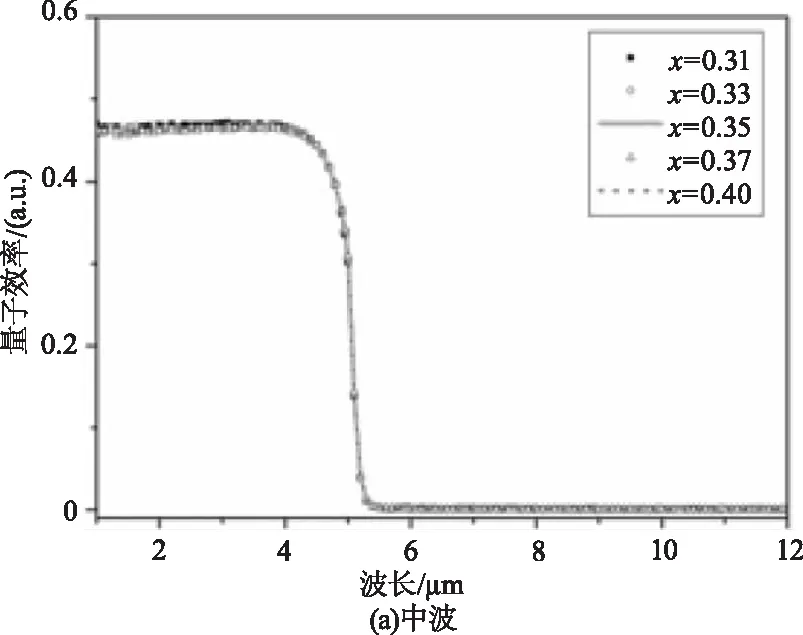
图11 中波和长波像元的量子效率 随阻挡层组分变化的关系Fig.11 The relationship between the quantum efficiency of medium-wave and long-wave infrared pixels with the composition of barrier layer

只有阻挡层组分为0.31时,长波像元对中波存在较大响应,这是因为此时阻挡层与中波层的导带带阶小,在中波层产生的光生载流子越过带阶势垒,进入长波层而被长波像元收集形成光响应。其他阻挡层组分下中波对长波的串音为2.21 %。

3.3 阻挡层厚度为0.1 μm时阻挡层组分对光谱串音的影响

接下来研究了器件的阻挡层厚度为0.1 μm时阻挡层组分对光谱串音的影响,器件结构如图1所示。如图12所示为阻挡层厚度为0.1 μm时中波(a)和长波(b)像元的量子效率随阻挡层组分变化的关系。如图12(a)所示,当阻挡层厚度为0.1 μm时,即使阻挡层组分达到0.45,也存在较大的长波对中波的串音。当阻挡层组分低于0.37时,长波对中波的串音约为15 %；阻挡层组分为0.4和0.45时,长波对中波的串音约为10 %。主要原因是阻挡层为0.1 μm时,量子隧穿效应强,存在长波层产生的光生载流子通过量子隧穿进入中波层,从而被中波像元收集形成响应。进一步提高阻挡层组分可以进一步抑制长波对中波的串音,但是生长难度将增加。可采用增加阻挡层厚度的方式抑制串音。如图13所示为阻挡层厚度为0.1 μm时中波对长波的串音随阻挡层组分变化的关系。随着阻挡层组分的增加,中波对长波的串音逐渐减小并趋于稳定,主要原因是组分增大,阻挡层与中波层的导带带阶大,中波层产生的光生载流子跃迁过带阶势垒的几率减少,使得中波对长波的串音减小。

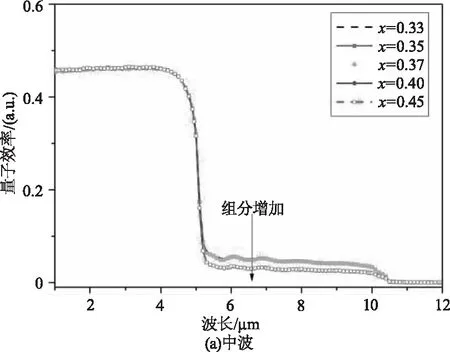
图12 阻挡层厚度为0.1 μm时中波和 长波像元的量子效率随阻挡层组分变化的关系Fig.12 The relationship between the quantum efficiency of medium-wave and long-wave infrared pixels with the composition of barrier layer when the thickness of the barrier layer is 0.1 μm

图13 阻挡层厚度为0.1 μm时中波对长波的 串音随阻挡层组分变化的关系Fig.13 The relationship between medium-wave to long-wave crosstalk with the composition of the barrier layer when the thickness of the barrier layer is 0.1μm

3.4 阻挡层厚度对光谱串音的影响

最后研究了器件的阻挡层厚度对光谱串音的影响,阻挡层组分分别选取0.33、0.35和0.37。如图14所示为阻挡层组分为0.37时中波和长波像元的量子效率随阻挡层厚度变化的关系,组分为0.33和0.35时量子效率谱类似,只是串音大小有差别。阻挡层厚度大于0.1 μm时三个阻挡层组分条件下长波对中波的串音随阻挡层厚度变化很小,串音约为2.1 %。

图14 阻挡层组分为0.37时中波和长波 像元的量子效率随阻挡层厚度变化的关系Fig.14 The relationship between the quantum efficiency of medium-wave and long-wave infrared pixels with the thickness of barrier layer when the barrier layer composition is 0.37

如图15所示为中波对长波的串音随阻挡层厚度变化的关系。随着阻挡层厚度增加,中波对长波的串音减小,因为阻挡层厚度增加,量子隧穿效应减弱,导致串音减小。当阻挡层组分由0.33增加至0.35以上是,中波对长波的串音大幅减小,而组分为0.35与0.37时串音已经减小至2 %左右,且厚度增加对串音的影响小,所以器件阻挡层组分选择0.35以上,厚度为0.3 μm以上,可保证中波对长波的串音以及长波对中波的串音都控制在2.5 %以下。

图15 中波对长波的串音随阻挡层厚度变化的关系Fig.15 Crosstalk of medium-wave to long-wave with the thickness of barrier layer

4 结 论

本文主要利用Crosslight公司的APSYS软件模拟准平面结构中长波双色碲镉汞探测器,包括准平面器件结构、碲镉汞吸收系数模型等初步建模。同时采用非抛物线型的吸收系数模型计算碲镉汞材料的吸收系数。研究表明中波层厚度增加将抑制中波对长波的串音,同时将小幅增大长波对中波的串音；阻挡层组分越大,阻挡层与中波层的导带带阶越大,光生载流子跃迁过带阶势垒的几率减少,使得串音减小；阻挡层厚度越大量子隧穿效应减弱,导致串音减小。最终通过模拟分析,中波层厚度为6 μm,阻挡层组分为0.35以上,阻挡层厚度为0.3 μm以上,结合生长难度和进一步抑制串音,可提高阻挡层组分和宽度,以使中波对长波的串音以及长波对中波的串音都控制在2.5 %以下。