共振直驱式浮力摆波能发电装置动力学研究

姚 涛，王志华，张旭东，王玉龙

（1.河北工业大学 机械工程学院，天津 300130； 2. 河北工业大学 国家技术创新方法与实施工具工程技术研究中心，天津 300401；3. 河北工业大学 电气工程学院，天津 300130；4. 潍坊科技学院，山东 寿光 262700）

浮力摆式波能转换装置结构简单，能够较好地适应波浪运动的大推力和低频特性。传统的浮力摆波能转换装置大多基于液压传动系统实现能量转换，如日本室兰大学最早提出的摆式波浪能发电技术，利用波浪往复运动作用在浮力摆上的力推动液压回路活塞，从而带动液压马达发电机发电[1]。英国爱丁堡大学的Henderson R 教授提出了新型液压系统波浪能发电装置[2]。液压转换具有传动平缓、输出稳定等优点，但是存在能量转换中间环节较多、损失效率高等不足。直驱式波能转换装置可用来直接发电，转换过程无需增加变速器，也不存在液压转换中的能量损失。1993年，Archimedes Wave Swing（AWS）项目组开始对永磁直线电机波浪发电进行研究，实现了全浸式浮体与发电机同体驱动发电[3]。1998 年，美国俄亥俄州立大学同Columbia Power Inc 公司合作研究了永磁直线波浪能发电机理，并于2010 年研发了1 kW 的SeaBeav，采用圆筒型永磁直线发电机进行电能转换[4]。

波能利用效率是波能技术研究的主要问题，共振状态下波能系统具备效率高、聚集能力强的特点[5]，因而利用共振技术是实现波能系统效率提升的有效方法。目前的研究中，波能转换装置的共振可通过变化俘能机构的刚度或质量、控制振动相位的方式来实现。如蔡元奇[6]通过重力平衡器消除由重力引起的强几何非线性，由变刚度装置调节波能装置的刚度实现波能系统的共振。由于波能系统中存在复杂的流固耦合及非线性行为，波浪能发电装置动力学性能的准确评估是计算波能转换效率的关键，也是共振装置优化设计的前提[7]。悉尼大学Caska A J 等[8]根据绕射理论计算激振力和辐射力，采用Morsion 公式中的拖曳力项，考虑粘性影响，分析了圆柱形浮力摆装置的水动力性能。天津大学田育丰等[9]采用k-ε 湍流模型对无PTO 阻尼悬挂摆水动力学性能进行了数值模拟，主要分析了摆板摆角以及摆板附近的波态。李威等[10]应用ADAMS/MATLAB 耦合仿真技术，分析浮力摆安装海域海况参数和浮力摆运行参数变化对浮力摆运动规律的影响。李雪临等[11-12]基于SPH-ALE 方法进行了浮力摆水动力数值模拟，并以浮力摆式波浪能发电装置为研究对象，以摆板的时均输出功率为优化目标，对摆板的迎浪宽度、质量分布、摆板结构形式等进行水动力性能优化分析。刘成果[13]对波浪条件和质量分布对底部铰接的浮力摆式波能转换装置的水动力性能的影响进行了实验研究。

本文提出一种共振直驱式浮力摆波能转换装置，发电模块通过弹簧实现振动控制，并通过摇杆—滑块机构方式固定于平台上，结构不仅利于维护，而且避免了发电模块所受到的海水腐蚀。计算波浪激励下浮力摆驱动直线发电装置的动力响应，对比分析不同弹簧—质量直线发电模块的动力学响应，从而揭示其共振机制。

1 理论分析

1.1 系统发电模型及运动控制方程

为有效提升波能转换效率，基于摇杆—滑块模型设计了一种直驱式浮力摆波能发电装置，其机构简图如图1 所示。在周期性波浪力作用下，浮力摆驱动固定于波面上某一位置处直线发电模块的动子做往复直线运动。动子上安装有永磁体，运动时与位于定子处的线圈形成电磁感应，从而实现发电功能。依据感应电动势公式：E=ΔΦ/Δt=BLv，增大动子与定子的相对运动速度可实现感应电动势的增加，而动子速度的提升可通过调节发电模块处的连接弹簧系数与波浪激励形成共振的方式实现。

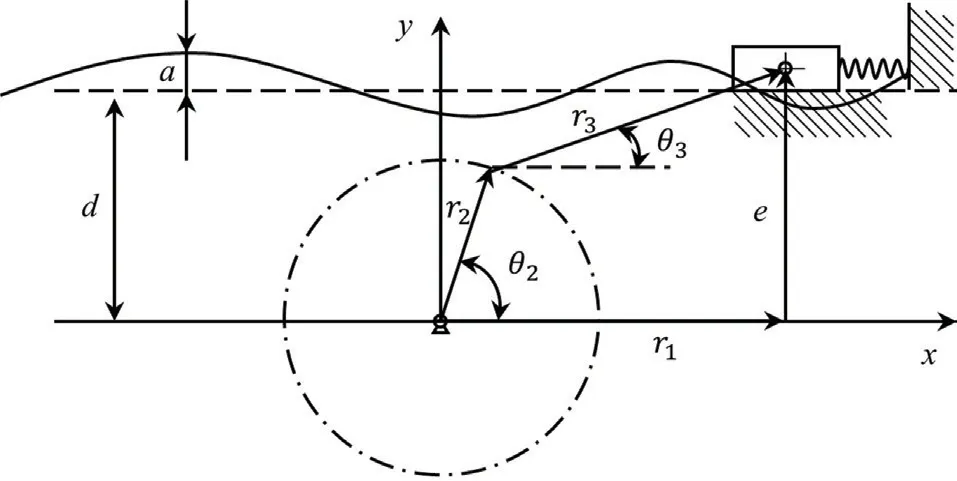
图1 浮力摆驱动直线发电系统

以铰接于水底的摆板支点O 作为坐标原点，海床平面为x 轴，水深方向为y 轴，建立坐标系，且静止状态下摆板中心线处于竖直状态，系统可看作是基于广义坐标下(r1, θ2)的二自由度运动，θ2为浮力摆的角位移，r1为发电滑块模块的位移；r2为浮力摆的长度，r3为连杆的长度，θ3为连杆与直线发电模块的夹角。

基于摇杆-滑块运动学关系原理，存在：

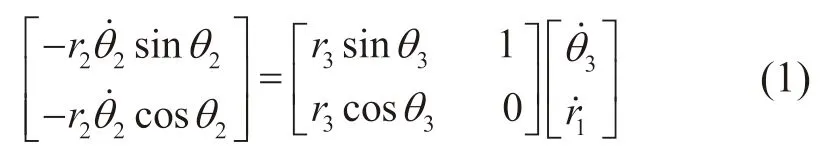
建立动力学控制方程为：

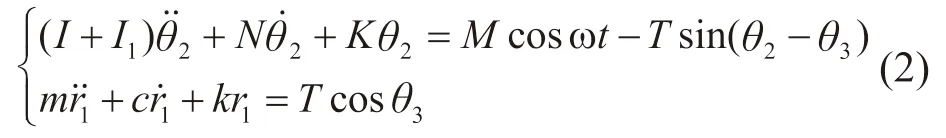
式中：I 为浮力摆的转动惯量；I1为附加惯性矩；K 为恢复力系数；δ 为浮力摆厚度，令ζ=δ/2；ρ 为海水密度；ρ0为摆板密度。对于矩形截面（长度r2，宽度B）摆板：

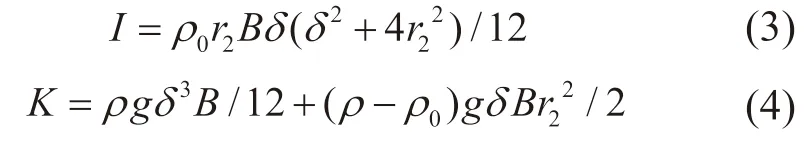
式中：N 为摆板在水中摆动的阻尼系数；θ2为浮力摆摆角；M 为波浪产生的激振力矩振幅；T为中间连接杆拉力；ω 为波浪的圆频率；t 为时间变量。

波幅为α，波数为k，激振力矩M 可通过对动水压强的积分求得，表示为：

联立上述式（1）和式（2）可获得摆板与直线发电模块的运动规律。

1.2 基于势流理论的动水压力计算

由自由表面运动学边界条件，理想流体非定常无旋运动拉格朗日积分式为：

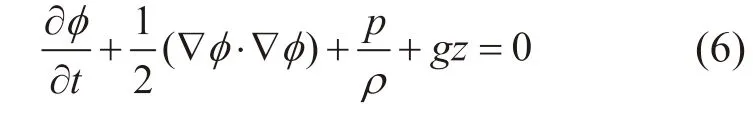
计算中如不考虑摆的圆弧过渡面，设计的浮力摆迎波面可近似为L×B的矩形，研究区域为中等水波区，波速与波长存在以下关系：

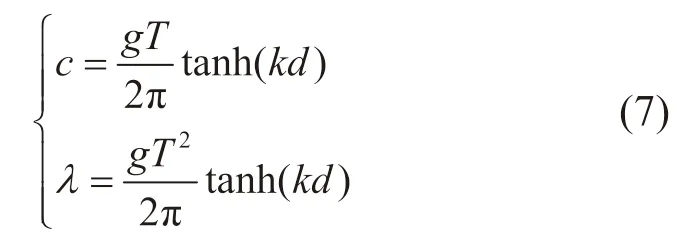
式 中：T=4s为 周 期，λ为 波 长，k为 波数（k=2π/λ），水深d=5 m。利用迭代求解的方法可得波长λ=22.18 m，则，符合有限水深条件。

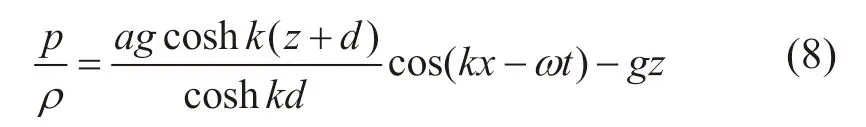
波面方程为：acos(kx-ωt)=η，其中a为振幅。

可得有限水深线性波作用下水域压力场分布：

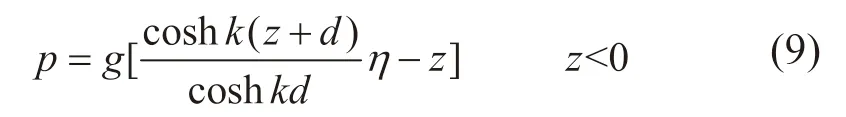
上式中右边第一项表示压力场的动水压强，第二项表示压力场的静水压强。当浮力摆处于竖直位置时，存在x=0，由式（8）可知，压力场分布为：

其中动水压力表示为：

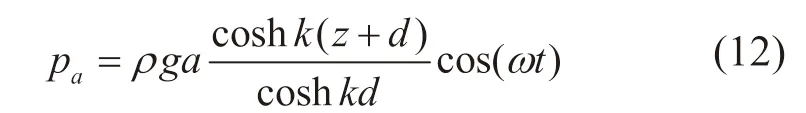
当浮力摆处于垂直水平面时，所受的波浪力最大，其值由压力场在浮力摆平面上的积分求得。

浮力摆所受波浪作用的波浪力为：

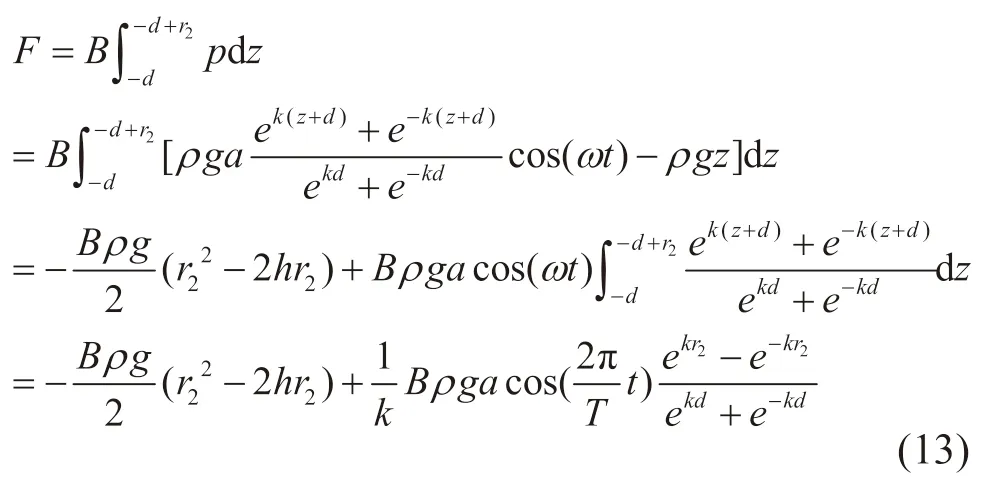
忽略静水压产生的作用力，浮力摆处于中间位置时，长方形浮力摆所受微幅波作用下的波浪力可简化为：

所设计浮力摆几何参数为：摆高r2=3.5 m，摆宽B=2.0 m，摆厚δ=0.1 m，摆选取密度ρ=1 023 kg/m3的轻质材料。波浪域选浙江省舟山群岛附近海域，波幅a=0.3 m，周期T=4 s，波长λ=22.18 m，波数k=2π/λ=0.2833 。根据上述所给的浮力摆参数和波浪参数，浮力摆所受微幅波作用下的波浪力：

2 流固耦合数值计算

2.1 仿真模型建立

流体域设定为规则的长方体，海岸底部为平面。考虑流体粘性作用，建立N-S控制方程式：

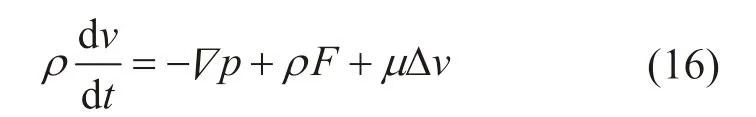
式中：Δ是拉普拉斯算子。水槽长度设定为30 m，流域高度即水深设置为5 m。为使反射波有足够长的距离消波，减小反射的影响，浮力摆距离造波源10 m 处。直线发电模块质量设为20 kg。

流体与浮力摆接触面设置为流固耦合边界。流体域的两个侧壁和底面均设置为固壁边界条件，由于侧壁对应为假想水体截面，故设为可滑移表面。底面为岸底不可滑表面。底面为岸底不可滑表面。流体域上表面设置为自由表面边界条件。右端面设置为具有对称边界的出流面，有效减小反射波，保证比较理想的消波效果。图2 所示为流体域边界条件设置图，同时显示了在9.8 s 时刻所施加的入口流速。

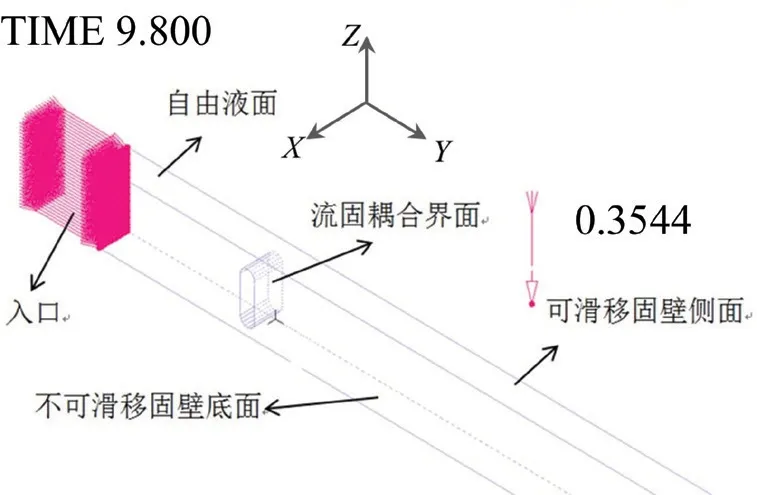
图2 流体域边界条件示意图

2.2 浮力摆流固耦合水动力学分析

图3 为波浪流域左端施加速度v=0.5sin(0.5πt)的边界条件时，在4 s, 6 s, 10 s, 14 s 时刻流体质点的位移。由图可知，距离左端造波边界越近，其波面质点Z向位移峰值越高，最高峰值达到0.5 m，随着波浪的向前传播，波面峰值呈下降趋势。大约在第4 s 时刻，迎波波浪传递至浮力摆位置处，浮力摆开始摆动，浮力摆上方波浪质点位移峰值保持在0.36 m 附近。图4 为4 s 和14 s 时刻流域内流体质点Y向位移图，仅浮力摆周边流域内质点存在明显Y向位移，最大Y向位移为0.49 m，表明浮力摆与周边流域的流固耦合相互作用明显。图5 为4 s 和14 s 时刻流域流体质点沿Y向速度云图，第14 s 时刻流体质点沿Y向传递的速度云图，波浪质点沿Y轴方向速度最大为2.202 m/s，最大速度位于波面上，最小速度为-0.546 m/s，位于流域底面上。结合图4 的位移云图，反映了波浪质点椭圆运动轨迹的特性，靠近波面处流体质点轨迹椭圆运动范围较靠近底部运动范围大。

图3 不同时刻Z 向波面位移图

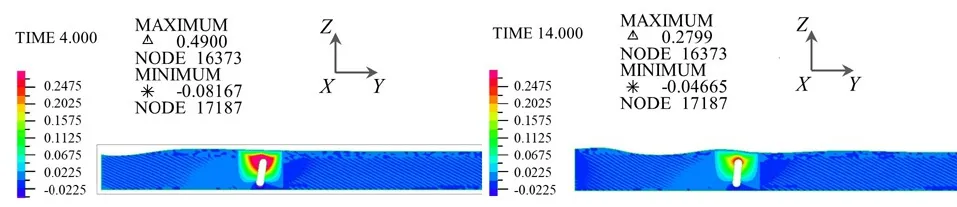
图4 不同时刻流域内流体质点Y 向位移图

图5 不同时刻流域内流体质点Y 向速度图

图6 为14 s 时刻流体质点速度矢量图，表明了流体质点相关时刻的速度大小与方向，反映了摆板在波浪中的运动状况及引起的流场变化。图7 为6 s 时刻节点水压力云图，表明位于流体域底部的水压力最大，最大流体节点压力为53 289 Pa，位于流域表面的水压最小，最小流体压力为-72.48 Pa。流体压力值为静水压与动水压之代数和，最小流体压力值为负值，产生于浮力摆顶部摆动方向的背向处，表明浮力摆沿Y向摆动时，浮力摆周边流域流速增大，从而导致背向流域流速降低，形成负压。

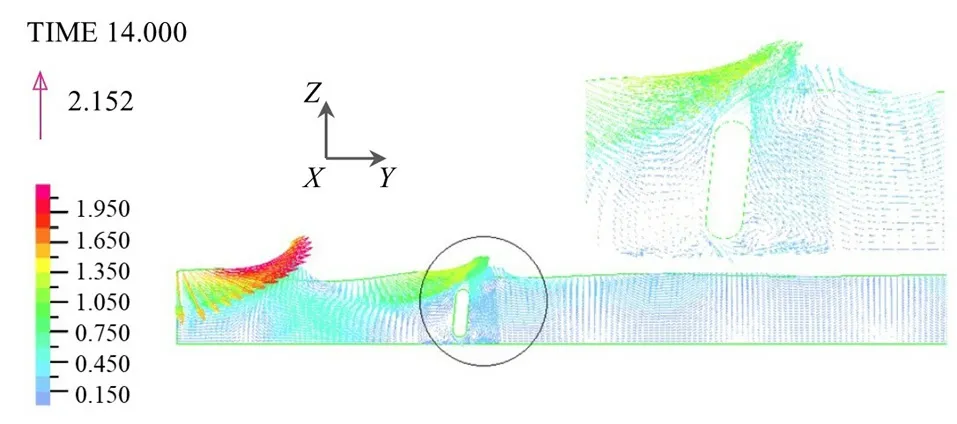
图6 14 s 时刻流体质点速度矢量

图7 6 s 时刻节点水压力云图

图8 为浮力摆在6 s, 12 s 时刻的流固耦合界面接触力分布云图。由左图6 s 时刻的云图中可以看出，流固耦合界面接触力随水深逐渐增大，其值介于66.7 ～466.7 N 之间，最大压力峰值出现在浮力摆下方，压力值为491 N。最小压力位于浮力摆上方圆角过渡处，压力为28.54 N。

图8 浮力摆在不同时刻处的流固耦合接触力分布

图9 所示为浮力摆在不同时刻的摆角，由图可以看出，在波浪力作用下，直线发电模块端不连接弹簧时，摆动最大幅度达到15 °，但是不能形成持续摆动趋势；而直线发电模块处弹簧刚度为800 N/m 时，可以形成摆动，但是摆动周期较长；当弹簧刚度系数为100 N/m 时，浮力摆摆动频率较高，并且能形成持续的摆动。

3 弹簧系数对发电模块运动学影响

图10 和图11 表示直线发电模块有无弹簧及不同弹簧系数时的运动速度及运动加速度。由图可以看出，当弹簧刚度系数为100 N/m 时，发电模块的速度和加速度呈现周期性变化，变化周期约为1 s，最大速度峰值为2 m/s，最大加速度峰值为18 m/s2。直线发电模块的质量为20 kg，当弹簧系数为100 N/m，可知模块的固有频率，当波浪周期为4 s 时，可知波浪圆频率。接近于模块固有频率ω=2πf=1.57，因此其运动响应较大。

图9 浮力摆在不同时刻的摆角图

图10 不同弹簧系数对发电模块速度的影响

图12 为3 种不同弹簧直线发电模块的加速度频率响应，从图中可以看出，弹簧系数为100 N/m的直线发电模块分别在0.75 Hz, 1.0 Hz, 1.75 Hz 频率处出现响应峰值，表明此频率处出现共振频率。无弹簧和弹簧刚度系数为800 N/m，加速度响应值较小。

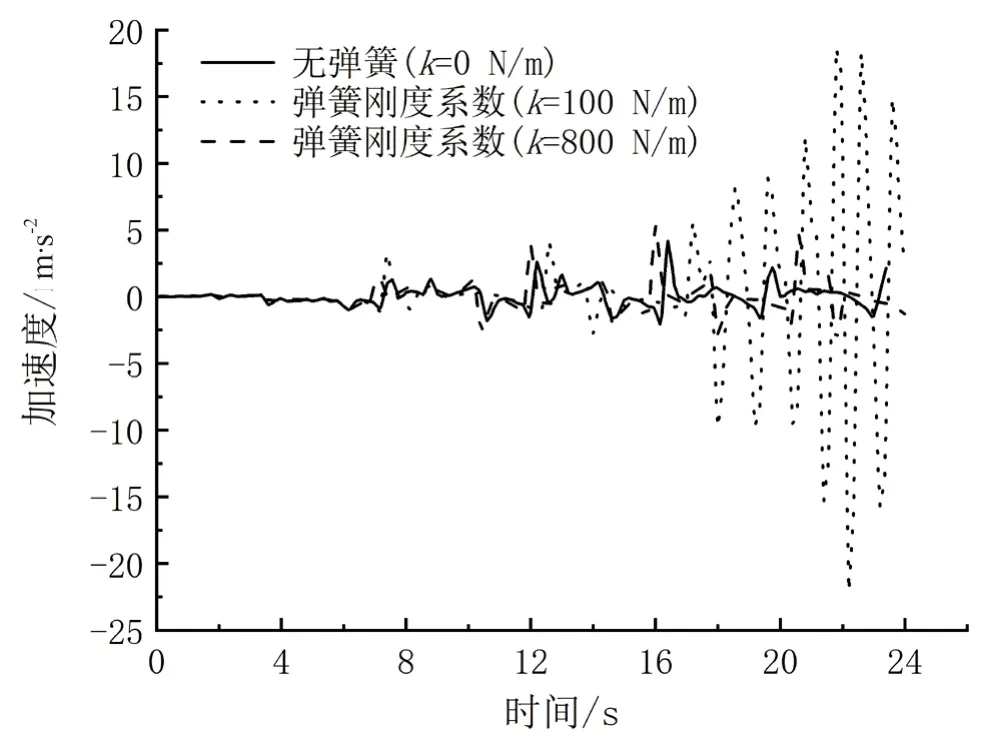
图11 不同弹簧系数对发电模块加速度的影响

图12 不同弹簧系数直线发电模块加速度响应频域对比

4 结 论

本文建立了浮力摆驱动直线发电模块模型，基于频域势流理论，推导了小幅线性波作用下摆板纵摇运动的激振力矩和水动力系数。基于ADINA 流固耦合仿真分析获得了浮力摆以及直线发电模块的运动响应。通过改变直线发电模块的弹簧刚度参数，得到以下结论：当直线发电模块固有频率接近于波浪频率时，可获得较高的发电效率，从而实现波浪转换效率的较大提升。另外，相比于浮力摆驱动液压缸，该装置省去了二级波能转换装置，避免了波能损失。