海底观测网海缆低阻抗故障识别及定位方法
2021-01-14冯迎宾刘文竹
冯迎宾,刘文竹,杨 昆,于 洋
(沈阳理工大学 自动化与电气工程学院,辽宁 沈阳 110059)
海洋约占地球表面积的70%,它对气候变化、生态循环、地质变迁以及人类活动具有重要作用。为探测和理解海洋的物理、化学、生物和地质等变化过程,海洋科学界提出了继地面/洋面和空间之后的第三个观测平台——海底观测网[1-2]。与传统的海洋观测技术相比,海底观测网的优点是观测平台位于海底以及能源供应和信息传输的网络化,实现了对海洋的长期、连续、实时的观测。因此,电能稳定、可靠的供给是海底观测网运行的基础[3-4]。
海底观测网采用海底光电复合缆(“海缆”)作为水下电能输送的载体[5]。海缆布设于海底,船舶抛锚、地壳变动、海洋微生物的腐蚀等都可能造成海缆绝缘层的破坏。海缆故障按照故障性质分为开路故障、高阻抗故障和低阻抗故障3 类。冯迎宾等[6]提出了利用残压识别海底观测网开路故障的方法,但未给出开路故障定位方法。曾祥君等[7]提出了一种基于多端故障行波时差的海底观测网故障定位方法,通过故障行波矩阵确定故障点位置,但未分析分支单元对行波传播的影响。海缆低阻抗故障是指海缆断裂,海缆中的供电导体与海水直接接触,供电导体会迅速被海水腐蚀,供电时间仅能维持十几分钟。为了提高观测网抗海缆故障的能力,周学军等和王希晨等[8-9]研究了海底观测网恒流供电系统方案,但恒流供电系统负载能力较差。Chan Ting 等[10]在假设低阻抗故障发生在某段海缆的条件下,对故障定位方法进行了分析,但未讨论故障点的识别算法,因此不具有实用性。李永倩等[11]针对海缆故障检测困难的问题,采用布里渊光时域反射技术建立了海底电缆实时在线检测系统。
针对海缆故障识别困难的问题,本文分析了海底观测网的供电模型、分支单元模型及海缆故障模型,利用稳压二极管的伏安特性,列出了岸基站与故障点之间的回路方程,求解故障点与岸基站之间的分支单元个数,从而识别发生故障的海缆。在故障识别的基础上,列出故障点与岸基站之间的回路方程,求解出故障点与分支单元之间的距离,实现故障点的定位。
1 海底观测网供电网络
海底观测网供电系统主要包括岸基站供电设备、海缆、分支单元、接驳盒等。岸基站供电设备向整个观测网提供电能;海缆是水下电能输送到接驳盒的载体,本文不考虑连接分支单元与接驳盒之间的海缆;分支单元是主电缆与分支电缆的交叉点,具有电缆故障隔离功能;接驳盒将传输的高压转换成低压为科学仪器提供电能并具有故障检测隔离的功能[12]。
海底观测网输电系统的拓扑结构主要类型:树型拓扑、环状拓扑、网状拓扑。由于网状拓扑结构具有抗故障能力强和负载能力强的优点,本文提出了一种网状海底观测网输电系统拓扑结构。输电系统拓扑结构如图1 所示,该结构包括2 个岸基站、11 个分支单元、9 个接驳盒。
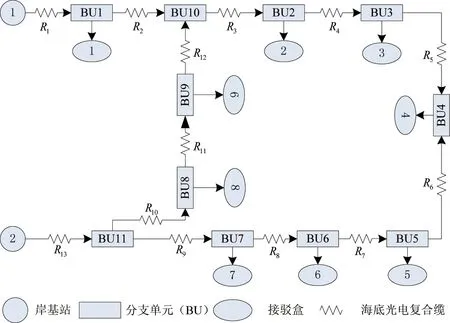
图1 海底观测网供电拓扑结构
1. 1 分支单元
潘立雪等[13]阐述了分支单元的工作原理和结构,其结构如图2所示。海缆存在低阻抗故障后,供电系统进入故障识别与定位模式,岸基站输出的电压低于接驳盒直流电压变换器的启动电压,海底观测网中只有主干电缆和低阻抗故障处有电流流过。由分支单元结构可知,分支单元内部含有2 对稳压二极管。当电流流过稳压二极管时,稳压二极管产生电压降,分支单元内部稳压二极管产生的电压降,可用公式(1)表示。
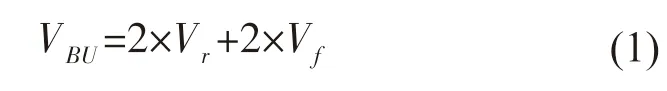
式中:VBU为分支单元两端电压降,Vr为稳压二极管反向导通电压,Vf为稳压二极管正向导通电压。假设分支单元选用的稳压二极管反向导通电压为6.2 V,正向导通电压为0.7 V,则分支单元两端的电压降13.8 V。
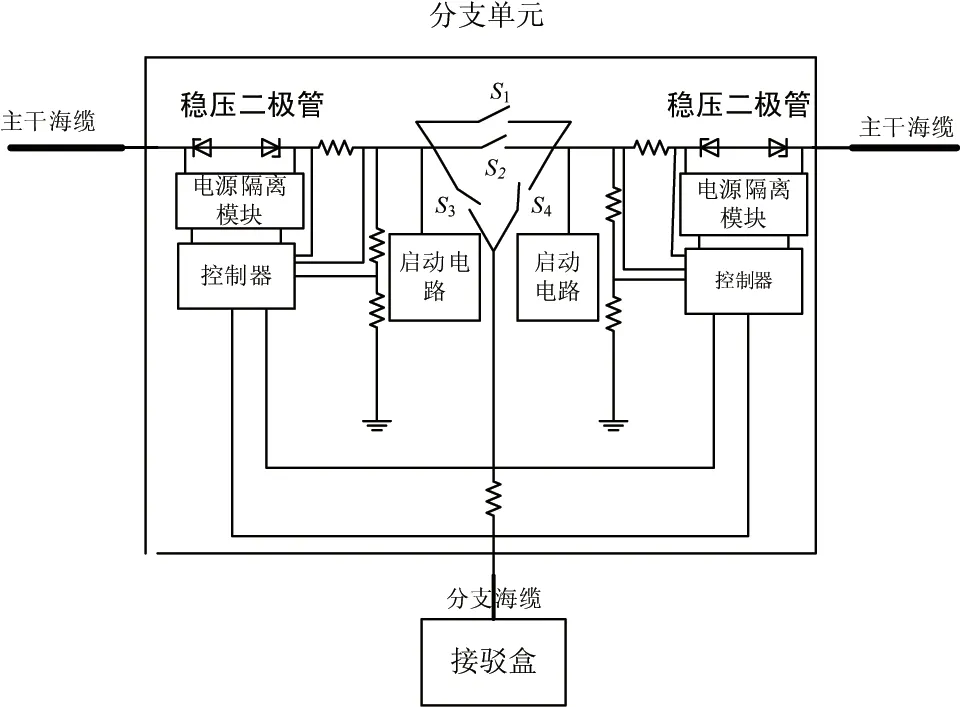
图2 分支单元结构
1. 2 海缆故障点
大部分海缆故障是由海缆绝缘皮损坏造成海缆导体与海水直接接触,导致供电回路短路。由于海水具有良好的导电性能,海缆导体与海水之间的电阻一般较小,因此称为低阻抗故障。海缆故障模型如图3 所示,假设位于分支单元a, b之间的海缆出现低阻抗故障,分支单元之间的距离用阻抗Rab表示,故障点f与分支单元a,b之间的距离可用N·Rab,M·Rab表示,其中M和N为比例系数,且M+N=1,故障点的阻抗可用Rf表示。

图3 海缆故障点
2 海缆故障识别方法
2. 1 海缆区域划分
由于海底观测网供电系统采用直流输电方式,因此可忽略容抗和感抗对供电系统的影响,只考虑海缆电阻对供电系统的影响。海缆的电阻与海缆的长度成正比,比例系数k=1 Ω/km,海缆可用海缆的阻抗R1, R2, R3…R13表示。海底观测网供电模型如图1,根据海缆的位置不同将海缆分成两个区域:位于环形网络的区域,包括海缆R3, R4,R5…R12;连接岸基站与环形网络的支路区域,包括海缆R1, R2, R13。
2. 2 稳压二极管特性分析
稳压二极管伏安特性曲线如图4 所示[14],可见其正向特性与普通二极管一样,在反向击穿区域内,反向电流在很大范围内变化时,其反向电压变化很小,基本上稳定在击穿电压附近。由式(1)可知,分支单元的电压降由所选取的稳压二极管决定,因此分支单元的电压降在适当的电流变化范围内电压降不变。在故障识别与定位模式下,可调节岸基站输出的电压,使分支单元的电压降保持不变,此时,岸基站输出的电流只受海缆电阻的影响。
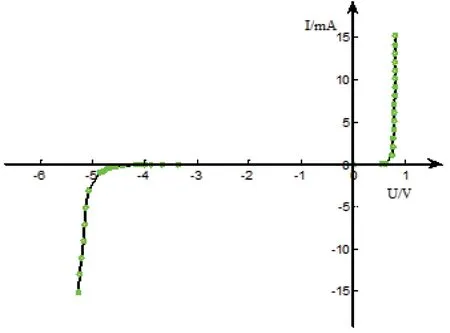
图4 稳压二极管伏安特性曲线
2. 3 故障海缆识别算法
假设如图1 的海底观测网出现低阻抗故障,供电系统进入故障识别与定位模式,仅利用岸基站1 就可实现故障海缆的识别。假设岸基站1 与故障点f 之间的阻抗为R,岸基站1 到故障点f 之间有n 个分支单元,因此,根据岸基站输出的电压U、电流值I 可写出如下方程:

式中:两个未知数n, R,可以调整岸基站输出电压,测得不同电压下的电流值,列出二元一次方程组求解两个未知数,方程组如式(3)。
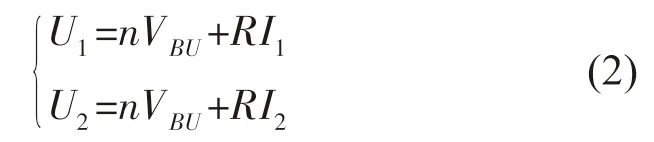
式中:U1, U2为岸基站1 输出电压;I1, I2为岸基站1 输出电流。解方程组可得:

根据海底观测网供电模型,当n=0 时,故障海缆为R1;当n=1 时,故障海缆为R2;当n>2 时,故障海缆位于环网,不能识别出发生故障的海缆。
如果故障海缆位于环网,节点分支单元10 的节点电压UBU10可表示为,
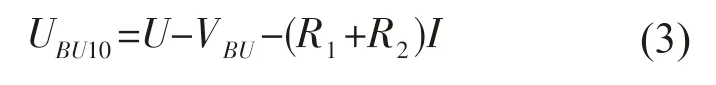
假设位于环网的海缆R5出现故障,根据拓扑结构,岸基站1 的输出电流可以通过两条路径到达故障点。假设两路径的阻抗为Rl1, Rl2,两路径所经过的分支单元个数分别为i, j。对节点分支单元10 可写出基尔霍夫电流方程:

式中:I 为岸基站的输出电流。对式(5)进行简化处理可得:
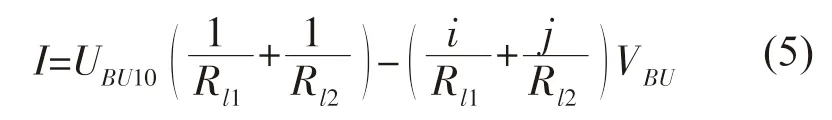
假设:
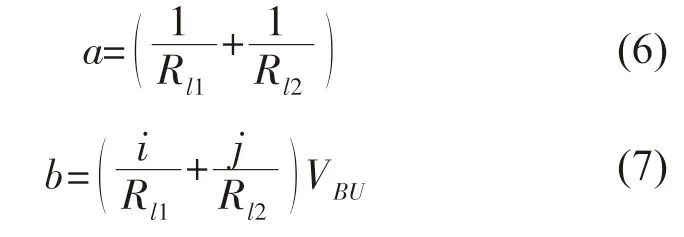
式(6)可简化成如下形式:

式中:UBU10可通过式(4)求得,I 为岸基站输出电流,可直接测量获得;a, b 为未知量。为提高计算精度,调节岸基站输出电压,获取多组数据求出变量a, b。假设调节岸基站输出电压4 次,岸基站输出电流矩阵,分支单元10 的电压矩阵:
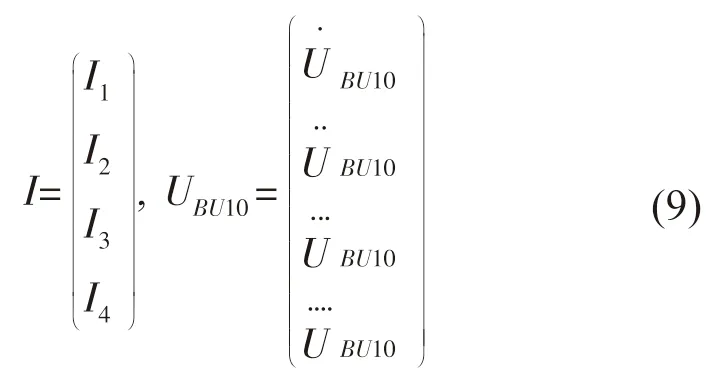
将式(9)写成矩阵的形式:
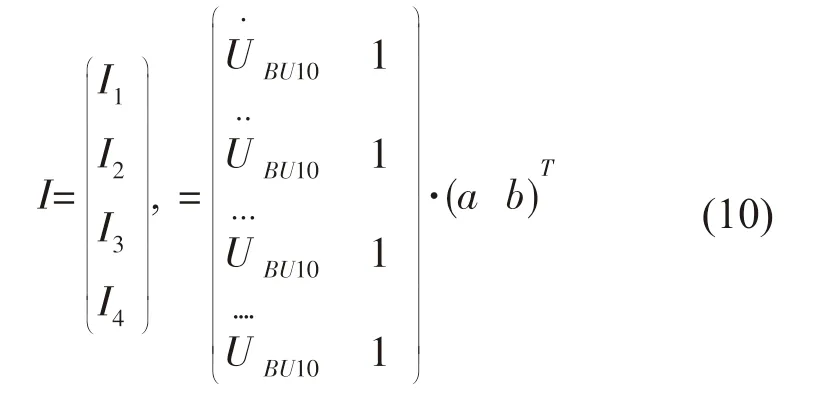
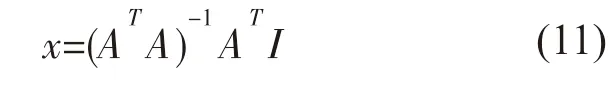
由于海底观测网的拓扑结构和每段海缆的长度和阻抗已知,因此可得如下方程:
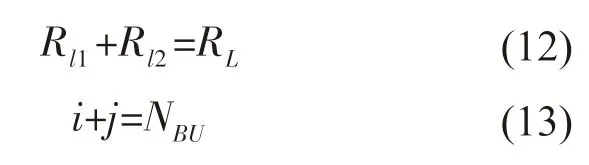
式中:RL为环网海缆的总阻抗;NBU为环网的分支单元总个数。
式(7 ~8)及式(12 ~13)构成方程组,可求出变量Rl1, Rl2, i, j。根据i, j 的值可得到存在故障的海缆。
3 故障定位算法
海缆位于海底,修复费用昂贵,维修周期长。海缆出现故障后,准确给出故障位置是提高海缆维修效率的关键。假设海缆R5存在低阻抗故障,利用本文2.3 节的中识别方法已经识别出发生故障的海缆。在故障定位模式下,由于供电系统输出的电压小于接驳盒电源转换系统的启动电压,接驳盒的负载没有启动。因此,观测网供电系统中只有故障点f 有漏电流,故障点漏电流If可表示为:

式中:IV1, IV2为岸基站1, 2 电源输出电流。
根据供电系统的拓扑结构可知,岸基站1, 2与故障点f 构成供电回路。采用支路电流法,可写出3 个独立方程。

式中:UV1、UV2为岸基站电源输出电压;Ii(i=1,2, 3…12)为各段海缆的电流;VBUi(i=1, 2, 3…11)为分支单元电压降,分支单元电压降相等。
根据海底观测网拓扑结构和基尔霍夫电流定律可知,
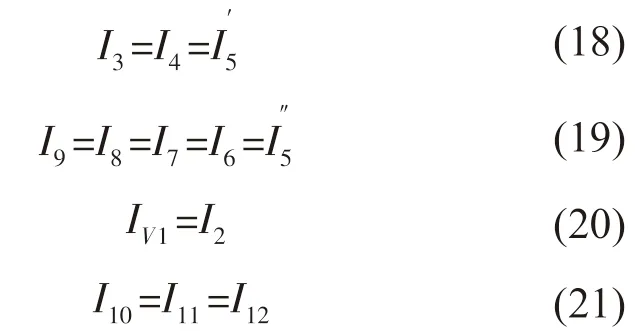
将式(18 ~21)代入式(15 ~17)可得:

节点BU11 可写出基尔霍夫电流方程:

由海缆故障模型可知:

式(14)及式(22 ~26)构成方程组,可求出未知量N, M, Rf, I3, I9, I10,从而实现对海缆故障点f 的定位。故障点f 与分支单元3 的距离L=NR5/k。
4 仿真实验
为验证算法的有效性,利用Simulink 电力系统工具箱SPS 模块建立了拓扑结构图1 的供电模型,仿真参数设置如下:岸基站电源电压1 和2 输出电压可调,输出电流可测,每段海缆的长度90 ~200 km 不等。假设电压、电流传感器测量误差服从均值为0、方差为0.1%的正态分布。
假设海缆R1,R2,R4,R5,R12分别出现低阻抗故障,根据式(3)计算n的值如表1。从表1 可以看出,根据n的值可以识别出低阻抗故障电缆R1,R2,故障海缆R4,R5, R12位于环网中,但不能直接识别出故障电缆。为了具体识别出环网中的哪支电缆出现故障,需做进一步的仿真分析,利用式(7 ~8)及式(12 ~13)计算出i,j的值,如表2 所示,可以根据i,j的值识别出现故障的海缆。

表1 不同区间的海缆故障求出的n 值

表2 不同区间的海缆故障求出的i,j 值
为验证故障识别算法不受故障点位置的影响,假设海缆R2出现低阻抗故障,故障点f与节点BU1 之间的距离在0 ~100 km 之间变化,每隔10 km 做一次仿真实验,故障点的阻抗为5 Ω,根据式(3)计算n,计算结果如图5 所示。从图中可以看出,可以通过n值识别出故障海缆R2,并且所求得n值与海缆故障点的位置无关。

图5 不同故障位置情况下的n 值
为验证故障识别算法不受故障点阻抗的影响,假设海缆R2故障点f与节点BU1 之间的距离为50 km,故障点f与海水之间的阻抗在0 ~10 Ω 之间变化,每隔1 Ω 做一次仿真实验,根据式(3)计算n的值,计算结果如图6 所示。从图中可以看出,可利用n识别出故障海缆,不受故障点与海水之间阻抗的影响。
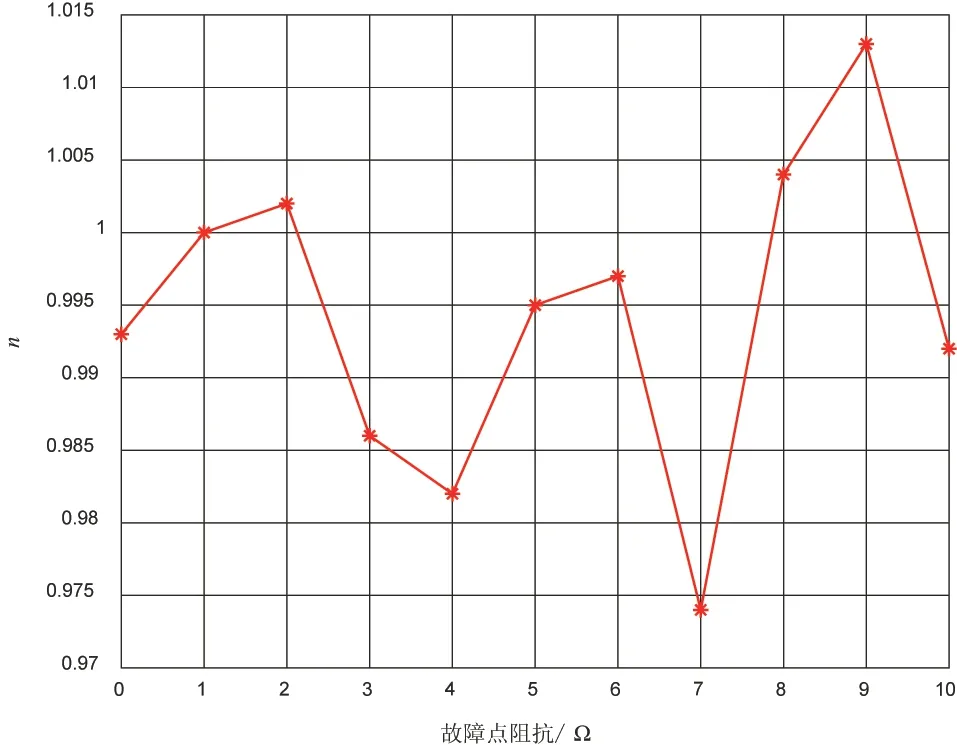
图6 不同故障点阻抗下的n
为验证故障定位算法,假设发生故障的海缆为R2,R4,R5,R6,R11。在故障海缆识别的基础上,利用式(14)及式(22 ~26)可计算出故障点位置及故障点阻抗,仿真结果见表3。从表3 可以看出,本文提出的海缆故障点定位方法在不同故障海缆的情况下实现了对故障点的定位,并且故障定位误差均在1 km 以内,同时给出了故障点阻抗。
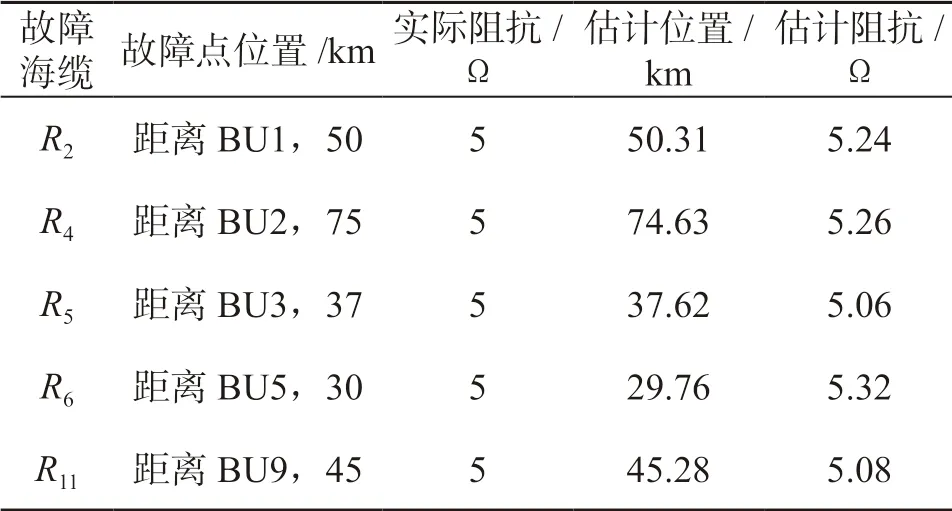
表3 故障海缆定位结果
为验证故障定位误差是否受故障点阻抗的影响,假设发生故障的海缆为R5,故障点与节点BU3 之间的距离为130 km,故障点f与海水之间的阻抗为0 ~10 Ω 不等,每隔1 Ω 做一次仿真实验。根据故障定位算法求出故障点位置,计算结果如图7 所示。从图中可以看出,本文所提出的故障定位方法不受故障点与海水之间阻抗的影响,故障定位误差均在1 km 以内。
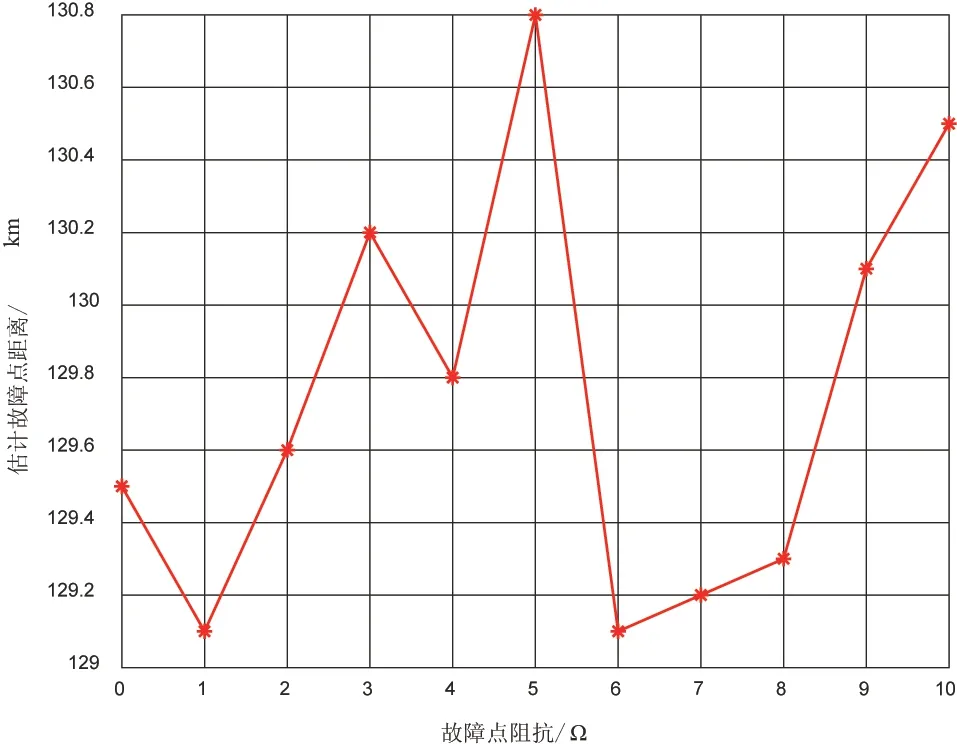
图7 不同故障点阻抗情况下的故障定位结果
5 结 论
本文在分析海底观测网络系统的供电模型、分支单元模型和故障电缆模型的基础上,提出了低阻抗海缆故障识别算法与定位算法。搭建了供电系统仿真模型,开展了仿真试验。试验结果表明:故障识别算法可精确识别发生故障的海缆,并且不受故障点阻抗和位置的影响;故障定位算法可计算出故障点位置,定位误差在1 km 以内,并且不受故障点阻抗的影响。在仿真试验的基础上,下一步搭建半物理仿真平台,验证本文算法在半物理平台的有效性。
