拖曳声源深度起伏对深海会聚区声传播损失测量的影响

李国富，张 爽，齐占峰，魏永星，周 莹，于金花，常 哲，秦玉峰

（国家海洋技术中心，天津 300112）

在水声调查实验中，声传播损失测量是一项非常重要的作业内容。目前，用于海洋声传播损失测量的声源主要有爆炸声源[1-2]和拖曳声源等[3-4]。拖曳声源具有支持人工设定发射信号、可重复使用、操作简便等优点，并且最小发声距离间隔可达几十米量级，可获得高空间采样率的声传播损失精细测量，因此成为当前海洋声学调查中的一类非常重要的发射声源[4-6]。在测量过程中，将拖曳声源布放在预定深度，按照一定时间间隔控制拖曳声源发声，并利用事先布放的水听器阵列接收经过海洋声信道的声传播信号，最终通过回放分析接收数据，得到声传播损失。

在深海中，会聚区现象是特有的声传播特征，更是深海水声调查的重要研究内容。会聚区传播的重要性在于它能够高强度、低失真地远距离传播声信号。利用会聚区效应，可实现对水中目标的远程探测以及水下装备的远距离通信等。会聚区声传播损失的准确测量在水声设备研制和水下对抗等方面具有重大意义[7]。然而，拖曳声源的拖缆长达数百米至数千米，在海流和航速变化的影响下，拖曳声源的深度必然发生起伏，由此导致会聚区声传播损失测量出现偏差。拖曳声源深度起伏对深海会聚区声传播损失测量的影响程度受到海洋声学调查研究人员的普遍关注，但目前对这一问题的系统分析研究还未见报道。

本文基于Argo 资料[8]和海洋声学RAM 声传播计算程序，对不同拖曳声源深度起伏幅度下的深海会聚区声传播损失进行了计算，通过对比分析获得了拖曳声源深度起伏对深海会聚区声传播损失测量的具体影响规律。

1 声传播损失计算方法

声传播损失的数值计算采用抛物近似声场计算程序RAM[9]，柱对称坐标系下的Helmholtz 公式为：

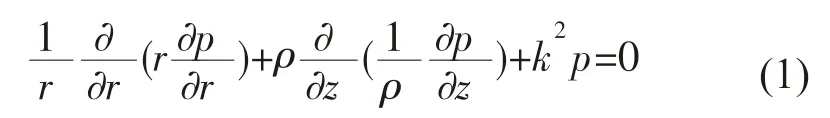
式中：波数k=ω/c(r,z)；c(r,z)为介质声速；ρ为介质密度。假设声压解的形式为：

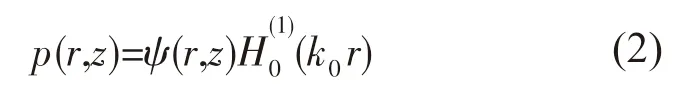
式中：k0为参考波数；H0(1)(k0r)为第一类零阶Hankel 函数。将式（2）代入式（1）中，经过推导可得到式（2）的发散波解：

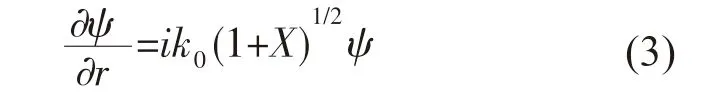
深度算子X 满足

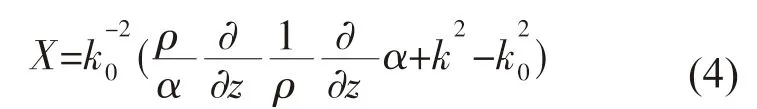
其中α=(ρ/k)1/2。

公式（3）的分裂步进Pade 近似解为：

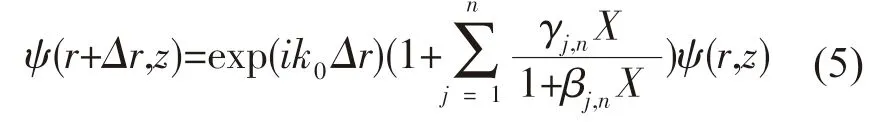
式中：γj,n和βj,n为复数系数。

应用Galerkin 法对深度算子X 进行离散化，将求解公式（5）转化为求解三对角线性公式组问题。对于点声源，RAM 计算程序采用如下自初始场：

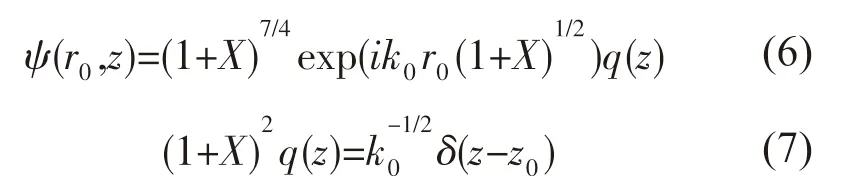
由式（5）～式（7）可计算出ψ(r,z)，然后代入式（2）得到声压p(r,z)，进一步计算可得不同深度和距离处的声传播损失：

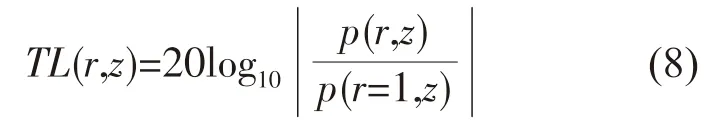
2 环境数据来源及声场计算参数

本研究采用的Argo 资料是由中国Argo 实时资料中心提供的全球海洋Argo 网格数据集，时间范围2004 年1 月—2017 年12 月，采样数据主要包括水温、盐度和压力，空间分辨率为1°×1°，剖面测量范围0 ～2 000 m，垂直层数58 层。该网格数据集是中国Argo 实时资料中心在各国Argo资料中心的实时和部分延时质量控制的基础上，利用逐步订正法，并结合混合层模型构建完成的全球海洋三维网格温、盐度资料集。

本文选取西太平洋某海域，该海域水深5 950 m（根据ETOPO1 数据），有较大深度余量，利于产生声场会聚现象。考虑到Argo 剖面数据的最大取样深度为2 000 m，无法提供声速剖面的深海部分，因而不能直接用于深海声传播计算。针对这个问题，2 000 m 以深部分，假设温度、盐度不变，只是压力增加，补齐温盐剖面，最后通过Chen&Millero 海水声速经验公式获得全海深的声速剖面[10-11]。

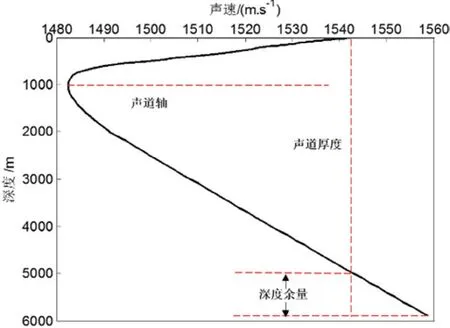
图1 西太平洋某海域5 月份平均声速剖面

图1 是利用上述方法计算得到的西太平洋某海域5 月份平均声速剖面，可以看出该海域的声速剖面呈现出典型深海Munk 剖面结构特征[12]。将声速剖面输入抛物公式RAM声场计算程序中，对该区域的声传播损失进行计算。声场计算过程中的主要参数设置如下：声源频率f=200 Hz、800 Hz，声源初始布放深度Z0=50 m, 100 m,300 m，接收深度200 m，海底深度5 950 m，海底声速cb=1 600 m/s，海底密度ρb=1.5 g/cm3，海底衰减系数αb=0.5 dB/λ。

在实际海上调查中，当拖曳声源沿着声传播测线发声作业时，由于海流速度和航速变化导致拖曳声源的垂直位置在初始布放深度附近上下起伏。假设拖曳声源的垂直位置Z 服从均值为Z0、起伏幅度为ΔZ 的均匀随机分布，即

在对拖曳声源深度起伏下的声传播损失进行仿真过程中，不同水平距离处的拖曳声源的垂直位置即声源深度按照式（9）计算，其他参数保持不变。在给定的声源深度起伏幅度下，声传播损失取20 次随机实现的平均结果。

3 结果与分析

3. 1 声源初始布放深度50 m 时的声传播损失

图2-a 和图2-b 分别给出了声源在50 m 深度，声源频率分别为200 Hz和800 Hz时的全海深声场。从图中可以看到，声场具有明显的会聚区特征，第一会聚区的中心距离在62.5 km 左右。另外在会聚区左侧可见较强的海底反射能量；在会聚区右侧，随着距离增加，海底反射损失不断增大，使得海底反射能量变弱。

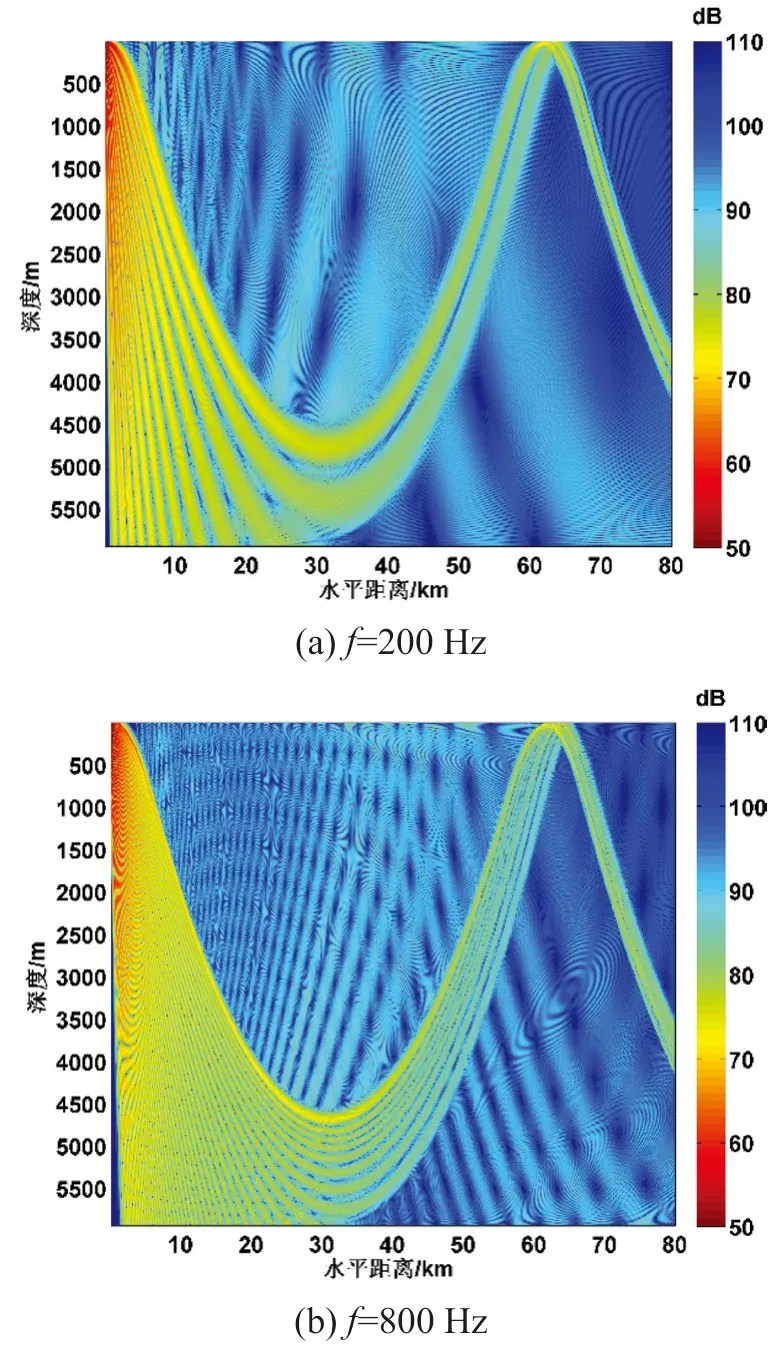
图2 声源位于50 m 深度的声场

为比较拖曳声源深度起伏对声传播损失测量的具体影响，图3 给出了拖曳声源初始布放深度Z0=50 m，不同深度起伏幅度下的声传播损失，并与声源深度稳定处于初始布放深度Z0时的声传播损失进行了对照。从图3-a 中可以看到，当声源频率f=200 Hz，声源深度起伏幅度为2 m 时，即声源深度在48 ～52 m 之间均匀随机变化时，水平距离30 km 以内的声传播损失出现误差（与图中蓝实线代表的Z0=50 m，且无深度起伏时的声传播损失相比），其他大部分水平距离的声传播损失基本无误差。在声源深度起伏不超过10 m 时会聚区的声传播损失误差几乎为零，在声源深度起伏为20 m 时会聚区声传播损失出现较小的误差；而会聚区左右两侧的海底反射区和声影区的声传播损失误差随着声源深度起伏幅度的增大而明显增大。图3-b 中，当声源频率f=800 Hz，在声源深度起伏幅度为2 m 时，会聚区声传播损失便开始出现一定误差，在80 km 以内的非会聚区声传播损失均出现较大误差。随着声源深度起伏幅度的增大，会聚区声传播损失误差有明显增加，但会聚区中心位置和宽度基本一致；非会聚区的声传播损失误差则变化不大。

图3 不同声源深度起伏幅度下的声传播损失（Z0=50 m）

3. 2 声源初始布放深度100 m 时的声传播损失

图4 为声源深度在100 m，声源频率分别为200 Hz 和800 Hz 时的全海深声场。与声源深度50 m时的声场结构相似，也呈现出明显的深海会聚区特征，第一会聚区的中心距离在62 km 左右。而与图2 所示声场的不同之处在于海底反射路径增多，海底反射能量的空间分布更加均匀。

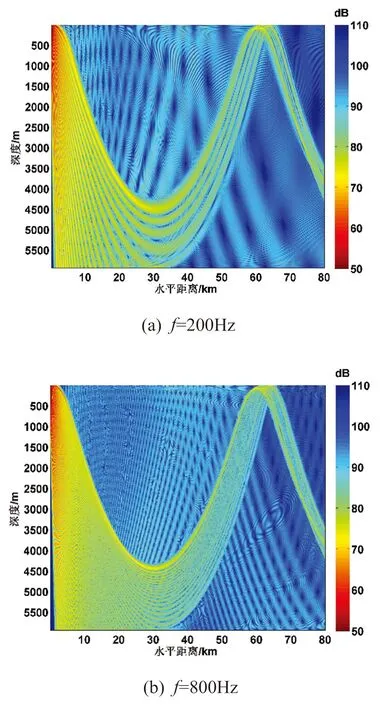
图4 声源位于100 m 深度的声场

图5 给出了声源初始布放深度Z0=100 m，不同深度起伏幅度下的声传播损失。从图5-a 中可以看到，当声源频率f=200 Hz 时，不同声源深度起伏幅度下的声传播损失误差变化与图3-a 声源初始布放深度Z0=50 m 时的情况基本一致，水平距离30 km 以内的声传播损失在声源深度起伏幅度为2 m 时即出现误差，声源深度起伏对会聚区声传播损失测量的影响远小于非会聚区。不同之处在于，会聚区声传播损失开始出现误差的声源深度起伏幅度变小，为10 m。图5-b 中，当声源频率f=800 Hz 时，声源深度起伏对声传播损失测量的影响比声源频率f=200 Hz 时更显著，这与声源初始布放深度Z0=50 m 时的情况类似。

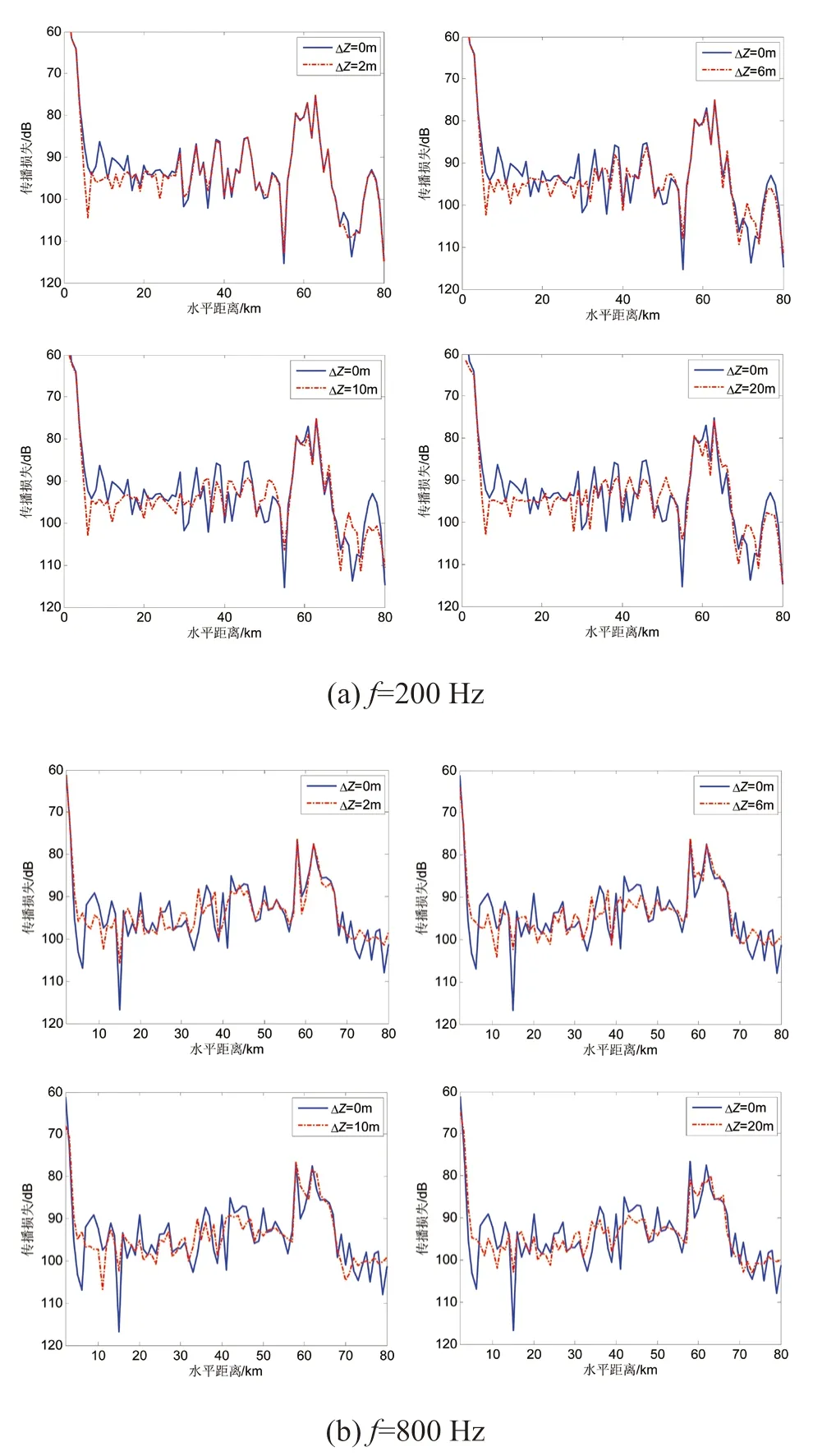
图5 不同声源深度起伏幅度下的声传播损失（Z0=100 m）

3. 3 声传播损失绝对误差

为定量分析拖曳声源深度起伏对深海声传播损失测量的影响，对3 个声源初始布放深度（Z0=50 m, 100 m, 300 m）下，不同声源深度起伏幅度(1 m ≤ΔZ ≤40 m)的声传播损失与声源深度稳定不变（ΔZ=0 m）时的声传播损失之间的绝对误差进行了计算。考虑到非会聚区和会聚区的绝对误差有较大差异，在下文分析中分别考虑非会聚区和会聚区的声传播损失绝对误差随声源深度起伏幅度的变化，如图6 所示。

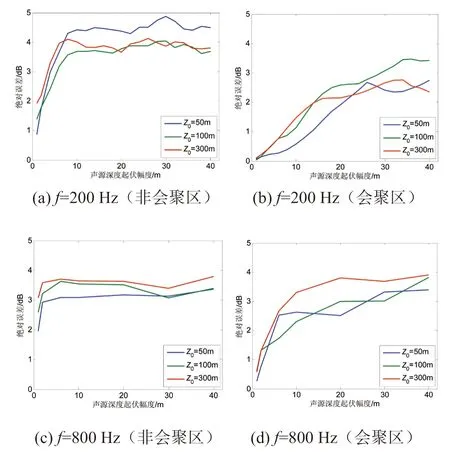
图6 不同声源深度起伏幅度下的声传播损失绝对误差

从图6 中可以看出，不同声源初始布放深度下的声传播损失变化具有相似的规律：声传播损失绝对误差随声源深度起伏幅度的增大而增大，当声源深度起伏幅度增大到一定数值后，误差则不再明显变化。具体而言，图6-a 显示非会聚区声传播损失绝对误差在声源深度起伏幅度ΔZ=1 m 时处于1 ～2 dB 之间，在声源深度起伏幅度增大到10 m 以后则基本稳定在5 dB 以下；图6-b 中，会聚区声传播损失绝对误差明显较小，在ΔZ=1 m 时仅有0.1 dB，当声源深度起伏幅度增大到40 m 时仍不足4 dB。对于声源初始布放深度Z0=50 m 的情况，声源深度起伏幅度ΔZ ≤10 m 时，会聚区声传播损失绝对误差不足0.5 dB；ΔZ=20 m 时，会聚区声传播损失绝对误差不足2 dB。这与图3-a的定性分析结果一致。另外，图6-c 和图6-d 显示，声源频率为800 Hz 时的声传播损失绝对误差与200 Hz 时的变化规律类似，明显不同之处在于声源深度起伏幅度ΔZ 较小时即有较大的声传播损失误差。

4 结 论

本文基于2004—2017 年的Argo 浮标资料，选取西太平洋某海域典型深海声速剖面，利用RAM 声场计算程序对不同声源深度和频率下的声场进行了计算，并对不同拖曳声源深度起伏幅度下获得的深海声传播损失进行了对比分析，得到如下结论：

（1）不同声源初始布放深度（Z0=50 m, 100 m,300 m）下，当声源深度起伏幅度在一定范围内(1 m ≤ΔZ ≤40 m)时，拖曳声源深度起伏对深海声传播损失测量具有相似的影响规律：声传播损失测量误差随声源深度起伏幅度的增大而增大，当声源深度起伏幅度增大到一定数值后，误差则不再明显变化。

（2）不同初始布放深度深度和声源频率下，拖曳声源深度起伏对会聚区范围内的声传播损失测量影响较小，对非会聚区范围内的声传播损失测量影响较大；

（3）水平距离30 km 以内的声传播损失受拖曳声源深度起伏的影响较大，即使在较低频率（f=200 Hz）、较小声源深度起伏幅度（ΔZ=2 m）时也会出现较大误差。

综上所述，拖曳声源深度起伏对深海声传播损失测量具有重要影响，较小的声源深度起伏对于高质量深海声传播数据的获取至关重要。在实际海上调查实验时，影响拖曳声源深度起伏的外部因素主要是实验船航速以及海流、海况变化，内部因素主要是拖曳声源的深度保持能力。由海流、海况变化引起的声源深度起伏问题可通过调整实验船航速令拖曳声源对水速度保持在一定范围内而获得一定程度地解决。相较而言，在拖曳声源设计、升级过程中，选择适当小的缆深比，减小拖缆阻力，降低拖缆拉力变化引起的深度起伏量，或者采用机动可变的翼板水阻设计，提高拖曳声源自身的深度保持能力是更重要的解决方案。