动态TailCoR模型的建模及其在金融市场中的实证研究*

叶五一，王天雄，缪柏其

(中国科学技术大学管理学院， 合肥 230026)

经过2007—2010年的金融危机和2009—2012年的欧债危机，越来越多的学者开始重视极端事件和尾部相关的研究。尾部相关的增加可能是由于线性相关性(当皮尔逊相关系数不等于0时)，也可能是由于一些非线性相关性引起的。关于尾部相关性的度量，学术研究涉及较多，但是对于其中的线性相关性和非线性相关性分解的研究并不多见。Poon等[1]提出，相比于线性不相关的投资组合，非线性相关的证券投资组合有着更厚的尾部分布。因此投资决策不仅取决于投资者的风险偏好，也取决于投资者对线性和非线性风险的偏好。

经典统计学通过线性相关系数刻画相关性，然而非线性相关在金融研究中十分常见，并且往往在危机时快速上升，引发严重后果。一般情况可以通过Granger因果检验对非线性相关关系进行研究，但由于无法对相关性的强弱给出准确的度量，不能适用于一些定量的风控模型。

近些年的研究中，学者更加关注相关系数的动态变化，DCC-GARCH是一种常用的研究动态线性相关系数的模型。DCC-GARCH模型从ARCH模型等一步步发展过来，Engle[2]提出ARCH模型，对时间序列的条件方差进行建模，历史的随机扰动项和当前的条件方差符合函数关系，这一模型对普遍存在异方差的金融时间序列建模效果较好。Bollerslev[3]在此基础上提出更一般的GARCH模型，GARCH模型中的条件方差是过去条件方差和随机扰动项的函数。随后Engle[4]提出DCC-GARCH模型，简化随时间变动的条件协方差矩阵的计算方法，并且得到不同变量之间动态时变的相关系数。

在尾部相关性的研究中，一个经常使用的方法是使用Copula模型和极值理论。该方法主要分为两步，第1步是假设分布的尾部渐近收敛速度为指数形式(边缘分布和联合分布都要满足)，第2步是使用极值Copula模型。Copula函数不限定边缘分布的形式，可以将用于反映相依关系的Copula函数和边缘分布分开研究，并可以研究变量之间的非线性、非对称的相关关系。Embrechts等[5]将Copula模型引入金融领域，迅速得到应用。Patton[6]构建动态Copula模型，基于ARMA模型的思想，假定Copula模型中的参数满足类似ARMA模型的演化形式。Rodríguez等[7]使用Copula模型，对各国股票市场指数之间的相关性进行研究。Copula模型虽然有以上诸多优点，但依然需要认识到它的局限性，Straetmans等[8]指出Copula在构建模型的时候需要假定变量服从于某种未知的分布，并且在估计时依赖对这个分布的参数估计，这不可避免地需要进行复杂的最优化，并且有些情形难以计算，造成一定的局限性。国内也有很多学者对尾部相关性的理论和应用进行研究。史道济和关静[9]利用Logistic条件模型和GEV条件模型分析1992—1999年沪深股市日内收盘价的对数利润数据。韦艳华和张世英[10]建立Copula-GARCH模型，对上海证券交易所各种指数收益率进行条件相关性研究。张明恒[11]利用Copula联结函数、混合分布和Jacob矩阵，构造多金融资产风险价值的Copula计量方法。

Ricci和Veredas[12]提出TailCoR模型，提供了研究尾部相关关系的一个新思路。TailCoR模型解决了Copula模型的一些局限性，比如不依赖于特定的分布，不需要最优化，在小样本下的性质表现良好。除刻画尾部相关性外，TailCoR模型在椭圆分布的假定下，可以直接将模型中的尾部相关系数分解成线性和非线性两部分(线性部分和非线性部分两个因式的乘积组成完整的尾部相关系数)，这有利于分析尾部相关性变化的原因，比如分析尾部相关性增加是由线性还是非线性相关性的上升引起的。文献[12]基于TailCoR模型分析美国和欧洲的大型商业银行股价收益率的尾部相关性，发现尾部相关性在2008年金融危机和欧债危机期间上升，更具体地，在2008年金融危机期间，线性和非线性相关性都有所上升，而在欧债危机期间，主要是非线性相关性的上升导致整体尾部相关性的上升。Geraci等[13]则基于TailCoR模型，研究卖空与股价变动的相关性。

TailCoR模型假定尾部相关系数是静态的，不随时间变化。要想观察TailCoR的动态变化，可以基于滑窗(比如一个季度)的方法进行刻画，在每个窗宽内得到一个TailCoR值，观察其随时间的变化趋势。由于TailCoR计算过程中，需要计算样本分位数，这就导致窗宽不能取得过短，因此基于滑窗的TailCoR模型对尾部相关性的刻画就不是很准确，而动态TailCoR模型可以解决这个问题。目前还没有学者基于TailCoR模型研究国内金融资产的尾部相关性。本文以TailCoR模型为基础，构建动态TailCoR模型，并进一步将尾部相关性分解成动态线性和非线性成分。在实证研究中，分别使用静态TailCoR模型和改进后的动态TailCoR模型，研究国内4家银行股价收益率之间的相关性，并分析尾部相关性随时间的变化趋势。

1 动态TailCoR模型的构建与尾部相关性的度量

1.1 TailCoR模型

在介绍TailCoR具体的计算公式之前，首先对TailCoR进行直观的解释。假设随机变量Xj和Xk在标准化后皮尔逊相关系数为正，那么点(Xj,Xk)出现在第1和第3象限的概率更高。存在一条穿过原点的直线θ=π/4，将所有的样本点投影到这条直线上，产生一个新的随机变量Zjk。直观理解，当两个随机变量正相关性很强，投影点会分散在整条直线上。而如果两个随机变量相关性不强，则投影点会集中在0附近。因此，可以用Zjk的上分位数和下分位数的差刻画两个随机变量的相关性强弱。

另外Zjk的上下分位数的差与尾部相关性也有关系。因为原点附近的数据对于分位数差没有影响，而尾部的数据对于分位数的差却有重要影响。图1将上述过程展现在坐标系中，下面给出TailCoR模型的具体构建过程。

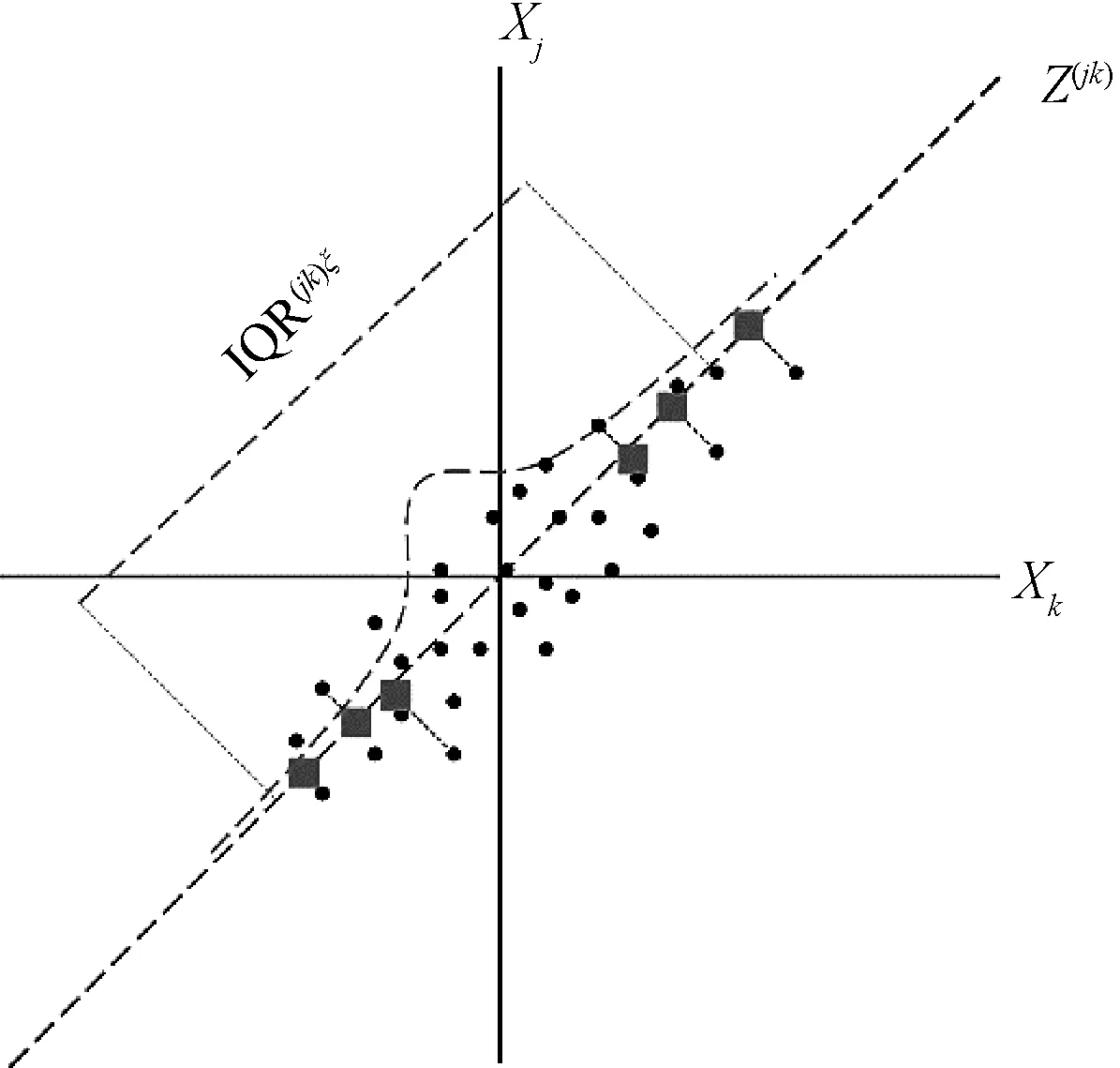
图1 TailCoR模型图示Fig.1 Diagrammatic representation of TailCoR

假设Xt,t=1,2,…,T是随机向量，维度是N，Xjt和Xkt是其中两个分量，下面给出Xjt和Xkt的尾部相关的度量过程。首先将Xjt进行处理，得到

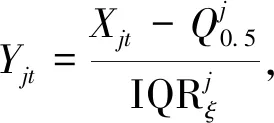
(1)

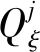
将(Yjt,Ykt)在直线θ=φ上投影，得到一个新的随机变量

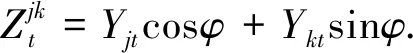
(2)

(3)

于是TailCoR定义如下

(4)

关于TailCoR模型，有如下几个性质:

2)类似于皮尔逊相关系数，输入两个离散时间序列样本，可以得到一个TailCoR数值，表示尾部相关性。值得注意的是，TailCoR并不在[-1,1]之间，当然也不以0为中心。实际上，由式(4)计算出的TailCoR大于1，且呈倒钟型分布。文献[12]基于蒙特卡洛模拟给出了TailCoR在不同分布下的形状。

3)如果Xjt和Xkt服从椭圆分布(概率等值线是椭圆形状，椭圆分布十分广泛，多元正态分布、多元学生t分布、多元指数分布等都是椭圆分布)，那么TailCoR有一些性质，文献[12]进行了严格的证明，下面仅给出结论。

首先，在椭圆分布的假定下，可以证明Xjt和Xkt正相关时，最佳投影线是第1象限角平分线θ=π/4，负相关时为θ=3π/4。

其次，TailCoR可以分解成线性和非线性两部分，如下：

(5)

具体证明过程见文献[12]。

容易看出TailCoR模型有以下几个优点。第一，TailCoR计算过程简单，不涉及复杂的方程求解和最优化；第二，在椭圆分布的假定下，TailCoR可以分解为线性和非线性两部分，便于分析TailCoR变化是线性相关性上升导致的还是非线性相关性导致的；第三，模型并没有假定原数据的分布情况，适用面更广。

1.2 非参数分位点回归模型

为了对TailCoR进行动态建模，需要基于非参数分位点回归模型对分位点进行动态估计。假定解释变量是一维，被解释变量和解释变量之间满足下面的方程

Yi=g(Xi)+uξi，

(6)

其中g(·)是待估函数，同时Qξ(uξi|X)=0，即uξi的条件分位点是0。于是Y的分位点和解释变量之间满足如下关系

Qξ(Y|X=x)=g(x).

(7)

通过局部常数分位点回归模型，可以得到分位点的估计。给定X=x，最小化下式可以得到参数a的估计：

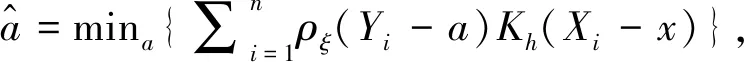
(8)

其中ρξ(u)=u·(ξ-I(u<0))。

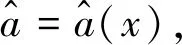
1.3 动态TailCoR模型

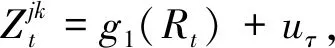
(9)

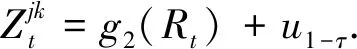
(10)

其中：Qτ(uτ|Rt)=0，Q1-τ(u1-τ|Rt)=0，即对应的条件分位数是0。

基于非参数分位数回归模型可以得到分位数的非参数估计

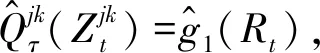
(11)

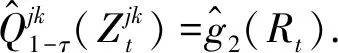
(12)

以上述分位数的估计替代式(3)，便可以得到动态TailCoR模型的估计

(13)

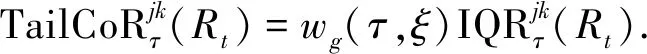
(14)

1.4 动态TailCoR模型的分解

在文献[12]提出的TailCoR模型中，基于椭圆分布的假设，将TailCoR分解成线性和非线性两部分，并在实证研究中发现TailCoR每次增加的原因是不同的，既可能是由于线性相关性增加而导致，也可能是非线性相关性增加而导致。为了使得动态TailCoR模型也能够进行类似分析，需要对动态TailCoR进行分解。

动态TailCoR模型可以依照式(5)进行分解，需要计算出线性和非线性相关性其中一个。Engle等[4]提出DCC-GARCH模型，简化了随时间变动的条件协方差矩阵的估计方法，并且得到了不同变量之间动态时变相关系数。基于DCC-GARCH模型可以得到动态线性相关系数的估计，进而得到动态非线性相关系数，下面给出具体的过程。

假定有k个资产，信息假定为独立同分布的白噪声过程，服从均值为0、协方差矩阵为Ht的多元正态分布，模型设定如下：

rt=μt+et，

(15)

et|Ωt～N(0,Ht)，

(16)

Ht=DtRtD′t.

(17)

其中：rt为资产收益率；Ωt为到t-1时刻的信息集；Dt从单变量GARCH模型中得到，得到条件标准差后取对角元素形成的对角矩阵就是Dt；Rt为动态条件相关系数矩阵，其结构为

(18)

(19)

(20)

以上对动态TailCoR模型进行介绍，同时给出分解后的动态线性相关系数和动态非线性相关系数，下面将该模型用于实证研究。

2 实证研究

2.1 数据和描述性分析

银行业务同质性较强，危机期间走势更加趋同，本文对银行股价收益率的相关性进行研究。样本方面，选择工商银行、中国银行、建设银行和招商银行，样本时间段为2008年1月2日到2018年6月29日(共2 553 d)。

本文希望观察尾部相关性在极端行情下的变化，所以希望样本覆盖较长区间，农业银行上市时间较晚，并不符合这一条件。选择招商银行的原因，除上市时间较长以外，股份制银行和4大行在业务模式、投资者类型等方面存在区别，有必要研究在极端市场环境下，股份制银行与4大行股价之间相关性如何变化。

在研究动态TailCoR模型时，本文引入上证综合指数的月度历史波动率作为解释变量，具体计算方法将在动态TailCoR的计算中进行介绍。

按照以下步骤进行实证研究：首先，进行描述性统计；其次，计算整个样本范围内的静态TailCoR以及相应的线性和非线性部分；再次，计算分段TailCoR，窗口宽度设定为半年，计算每个时间段的TailCoR及其线性和非线性部分，观察尾部相关性随时间的变化；最后，使用实际波动率作为外生变量计算出动态TailCoR，基于椭圆分布下的分解，先使用DCC-GARCH模型获得动态线性相关性系数，后获得动态非线性尾部相关性系数。

首先，对4家银行收益率进行描述性统计，并判断是否服从正态分布，结果见表1。

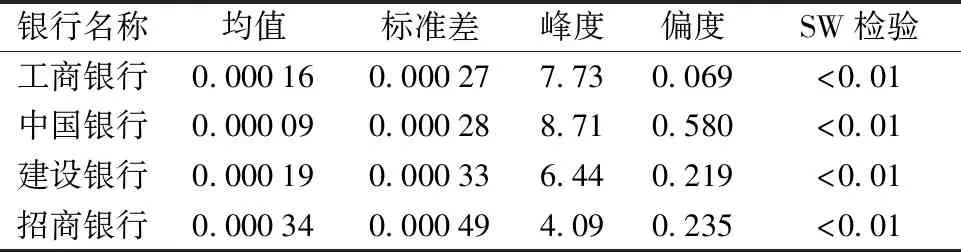
表1 4家银行收益率的描述性统计量和SW检验Table 1 Descriptive statistics and SW test of the yields of the four banks

从表1可以看出，招商银行收益率的标准差高于另外3家大型国有商业银行，股价波动性更高。且4家银行的收益率序列的峰度大于3，偏度大于0，显示出尖峰和右偏的特点。在SW检验的结果中，4个银行的p值均小于0.01，因此4个银行的收益率并不服从正态分布。后面将基于TailCoR模型测量和分析4个银行的尾部相关性。

2.2 4家银行间的静态TailCoR

根据上文中TailCoR的定义，容易得到静态TailCoR的计算步骤。在相关系数的估计方面，我们有所调整。Lindskog等[14]利用椭圆分布的几何性质，得出Kendall相关系数在椭圆分布族下不变。因此用样本Kendall相关系数来估计，结果稳健，公式如下

(21)

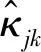
下面给出静态TailCoR的计算步骤，以及线性和非线性部分的分解，计算过程如下：

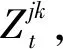
第2步，选择适当的系数wg(τ,ξ)，计算出

(22)

第3步，给出非线性相关系数的估计

(23)

通过椭圆分布的性质，可以得到TailCoR模型中的最佳投影线是θ=π/4。参数选择上，取ξ=0.75，τ=0.95，那么对应的wg(τ,ξ)=0.410(文献[12]的附录中有给出)。由此，可以计算出4家银行之间的TailCoR，如表2所示。

表2 4家银行收益率之间的TailCoRTable 2 TailCoR between the yields of the four banks

由表2可以看出，4家银行之间的10个TailCoR都接近2，说明它们之间的相关关系很类似。在表3和表4中，将TailCoR进行分解，观察线性部分ρ和非线性部分w(0.95,0.75,α)的情况。

表3 4家银行收益率的线性相关系数Table 3 Linear correlation coefficients of the four banks’ yields

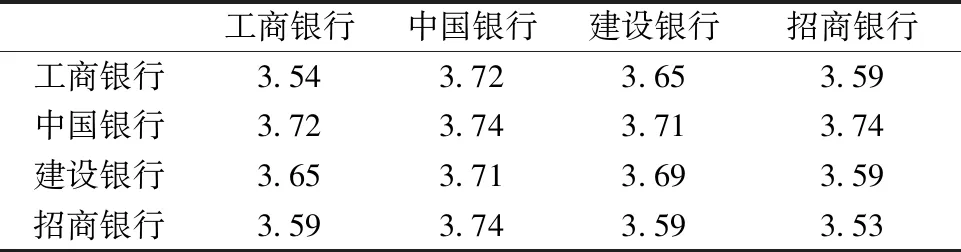
表4 4家银行收益率之间的尾部非线性相关系数Table 4 Tail nonlinear correlation coefficients between the yields of the four banks

Kendall相关系数矩阵与皮尔逊相关系数矩阵十分接近。对于线性相关性，大型商业银行之间相关性更强，招商银行与之偏弱。对于非线性相关性，各家银行相关性比较接近，招商银行和中国银行的非线性相关性更高。

接下来，观察尾部相关性随时间的变化，可以采用分段TailCoR模型来处理。将窗宽设定为半年，样本时间分为21个时间段，分别计算各个时间段的TailCoR，以观察尾部相关性如何随时间变化。

首先将4家银行的分段TailCoR显示在一个轴上，然后分别画出3家大型国有商业银行相互的TailCoR以及招商银行与大型国有商业银行之间的TailCoR，具体如图2所示。

图2 分段TailCoRFig.2 Segmented TailCoR

在2014年下半年牛市启动和2015年下半年牛市破灭的时候，3家大型国有商业银行的尾部相关性出现快速上升。而招商银行与其他3家大型银行之间的尾部相关性在牛市启动时快速上升，但是2015年泡沫破灭时相关性上升并不明显。下面比较4家银行TailCoR的线性和非线性成分的变化图，如图3所示。

图3 分段TailCoR分解Fig.3 Segmented TailCoR decomposition

从图3可以看出，动态线性相关系数在整个样本区间上变化幅度较小，尾部相关性的快速上行主要由非线性部分贡献。具体来看，非线性相关系数在正常状况下为3附近，极端情况下快速上行至5～6，推动尾部相关性出现明显抬升。

由分段TailCoR可以得到以下几条结论：第一，TailCoR总体上是稳定的，在2014年下半年和2015年下半年迅速增长；第二，大型商业银行的TailCoR值波动更大，招商银行与其他3家大型国有商业银行之间的TailCoR相对稳定，在2014年下半年牛市启动的时候招商银行和大型银行的尾部相关性较强，但是在2015年股灾的时候相关性上升并不明显；第三，TailCoR中的线性部分波动小且趋势较弱，TailCoR的快速上升主要由非线性相关性上升导致。

2.3 4家银行间的动态TailCoR

Ramchand和Susmel[15]通过SWARCH模型，得出当美国股票市场波动剧烈时，它与其他市场间的相关性会显著上升。市场波动率会对尾部相关性产生影响，因此本文选用市场历史波动率作为外生变量。

对于上证综合指数历史波动率计算如下：

rt=lnPt-lnPt-1，

(24)

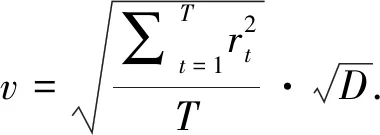
(25)

其中：Pt是上证综合指数日收盘价，D是该年的交易天数，T是该月的交易天数。

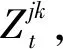
在非参数分位数回归模型中，选用正态核。对于窗宽，计算公式如下

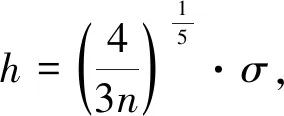
(26)

其中:σ是解释变量的标准差，n是解释变量的样本数。

图4 工行和中行间的和上证综指历史波动率的分位数回归结果Fig.4 Quantile regression results of the historical volatility of and Shanghai composite index between ICBC and BOC

将工商银行与工商银行、中国银行、建设银行和招商银行之间的TailCoR取均值，得到工商银行TailCoR的曲线，其余类推。图5 4家银行之间的动态TailCoRFig.5 Dynamic TailCoR between the four banks

由图5可以看出，在2008—2009年，4家银行的TailCoR均处于最高位置，这一阶段对应2008年股市泡沫破灭的过程。而静态TailCoR这一时间段，只有小幅度上升。在2014年下至2015年下，动态TailCoR出现了一个波峰，而静态TailCoR在2014年下、2015年下出现双峰。

下面基于DCC-GARCH模型，计算动态线性相关系数。首先，需要使用GARCH模型对边缘分布进行估计，这里使用GARCH(1,1)模型来拟合。模型如下：

ri,t=μ+σtεt，

(27)

(28)

其中εt独立同分布于标准正态。

将原数据标准化(减去均值再除以标准差)后，基于极大似然方法进行参数估计，表5给出GARCH(1,1)模型的估计结果，并给出了一些参数在不同置信度下的显著性检验结果。将GARCH(1,1)中的参数估计结果代入DCC-GARCH模型中，可以得到DCC-GARCH模型的参数估计结果，具体见表6。

表5 4家银行股票收益率GARCH(1,1)模型参数估计结果Table 5 Estimation results of the GARCH(1,1) model parameters of the four banks’ stock returns

表6 4家银行股票收益率DCC-GARCH模型参数估计结果Table 6 Estimation results of the DCC-GARCH model parameters of stock returns of the four banks

根据上述估计结果，代入DCC-GARCH模型中，可以得到动态线性相关系数，如图6所示。

图6 工商银行和中国银行间动态线性相关系数Fig.6 Dynamic linear correlation coefficient between ICBC and BOC

4家银行的动态线性相关系数走势相对平稳。到目前为止，通过引入非参数分位点回归模型，得到4家银行间的动态TailCoR，之后通过DCC-GARCH模型估计出动态线性相关系数。通过动态TailCoR和动态线性相关系数可以得到动态非线性相关部分，如图7所示。

图7 4家银行间动态非线性相关系数Fig.7 Dynamic nonlinear correlation coefficients between the four banks

可以看到动态非线性相关系数和动态TailCoR走势十分类似，可以认为4家银行间的TailCoR主要由非线性部分贡献。总体来看大型国有商业银行之间的TailCoR趋势性十分一致，在极端行情下尾部非线性相关系数更高，而极端情况下招商银行和其他3家大型国有商业银行的尾部相关性偏低，尾部相关性较小。

通过对动态TailCoR模型的分析，可以得到如下的结论：

第一，尾部相关性变化的原因主要是非线性相关部分，分段TailCoR模型和动态TailCoR模型都支持这一结论。在2008年和2014—2016年股票市场波动率加大时，尾部相关性上升主要是非线性部分上升导致。

第二，TailCoR在牛市启动和市场开始崩溃时会快速上升，其余时间保持稳定。

第三，中国工商银行，中国银行和中国建设银行的尾部相关性变化一致， 在极端的市场条件下，尾部相关系数会显著增加。但是，招商银行与3大国有商业银行之间的尾巴相关性相对稳定。

3 结论

在模型构建时，本文借鉴文献[12]提出的TailCoR模型，通过非参数分位点回归模型对模型中的分位点进行建模，得到时变的TailCoR，定义为动态TailCoR模型。

在样本服从椭圆分布的假定下，TailCoR可以进行分解，其中一部分包含皮尔逊相关系数，定义为线性相关部分，余下部分定义为非线性相关部分。本文通过DCC-GARCH模型得出动态线性相关系数，之后通过动态TailCoR和动态线性相关系数得到动态非线性相关系数。

在实证研究中，选取工商银行、中国银行、建设银行和招商银行在2008年1月至2018年6月29日的股价日收盘价收益率数据，通过原TailCoR模型、分段TailCoR模型和动态TailCoR模型，描绘4家银行股价的尾部相关性及其随时间的变化，得到以下结论：第一，尾部相关性主要是非线性部分贡献；第二，TailCoR代表的尾部相关性，在市场剧烈变动时上升，其余时间保持稳定；第三，工商银行、中国银行和建设银行的尾部相关性十分一致，并且上升十分迅速，而招商银行和3家大型国有商业银行的尾部相关性相对较低。