《认识二元一次方程组》起始课的分析与思考
2021-01-13江门市江海区礼乐中学
文/江门市江海区礼乐中学 钟 喜
本文以《认识二元一次方程组》为例介绍章节起始课的一种设计思路,实践表明,该设计可以较好地帮助学生初步建立起章节的内容框架,体会本章节的核心数学思想和通性通法,培养良好的数学思维方式与品质。
一、感悟核心背景,探索素养教学
数学要发展学生的数据分析、数学抽象、逻辑推理、数学建模 、数学运算等核心素养,学会用数学眼光观察世界,用数学思维分析世界,用数学语言表达世界。基于核心素养下的章节起始课要求教师要提纲挈领地呈现出本章的结构性知识链,抓住知识的本质,创设合适的教学情境,引发学生的深入思考,将抽象的知识通俗地讲解出来并帮助学生提炼出学习本章后续几节内容的规律和常用方法。
二、初探课例教学,融入数学素养
笔者在2019年广东省乡村骨干教师能力提升高端研修班(初中数学)跟岗学习期间,上了一节《认识二元一次方程组》的示范课,得到广东省名师吴有昌教授的点评和指导,我深刻地意识到章节起始课教学中数学知识的整体性与通性通法的重要性。现以课例为起点对《基于数学核心素养下起始课的教学》做一个深入探讨。
(一)类比建模,挖掘知识关联性,培养数学建模素养
数学知识往往是以结果的形式呈现出来的,然而数学教学更重要的是要向学生展示“结果”背后的过程。
1.情境引入
题目:昨天,我们8个人去红山公园玩,买门票花了34元,每张成人票5元,每张儿童票3元,他们到底去了几个成人,几个儿童呢?
分析:如果设去了x名成人,则去了(8-x)名儿童。
根据题意用已学的知识列出方程?
5x+3(8-x)=34
师:请问这是一个什么方程?具有什么特征?
生:一元一方程,只含有一个未知数,并且未知数的次数为1。
师:题中含有两个未知量且题中存在两个等量关系,能否大胆尝试设出两个未知数?
生:设去了x名成人,去了y名儿童。
师:根据等量关系列出方程。
设计意图:这节课是由一元一次方程进入二元一次方程的起始课,学生对一元一次方程的概念、解法以及应用都非常熟悉,所以利用类比一元一次方程的学习方法引入二元一次方程,并设计一题多解的方法,向学生呈现二元一次方程较一元一次方程的优越性,从而激发学生学习二元一次方程的欲望,使学生体会到知识的相连性,进一步培养和发展学生的方程思想,提升数学建模能力。
2.探究新知
师:这两个方程x+y=8、5x+3y=34具有什么特征?
生:具有两个未知数、并且未知数次数为1。
师:独立思考,小组讨论1分钟,类比一元一次方程概念,说说二元一次方程的概念。
设计意图:通过让学生观察、探索、类比得出二元一次方程的概念,把课堂交还给学生,充分体现学生自主学习的能动性。
(二)迁移应用,创新学习模式,培养数学运算与逻辑推理素养
弗莱登塔尔强调,学生将所学知识“数学化”,即对知识的“再创造”,在这个过程学生可以自己发现、创造,进而得出结论,并且学生有着较大的自主性,可以发展各种不同的数学思维和数学方法。
1.请每位同学写一个关于x、y的二元一次方程;
2.同桌两人把所写的二元一次方程联立起来;
设计意图:设计课堂活动让学生编题,把编写的二元一次方程联合起来“创造”出二元一次方程组,并且所编的题目将贯彻整一节课的教学,大大地提升了课堂设计的严谨性。
3.师:回忆一元一次方程的解?
生:使得一元一次方程左右两边相等的未知数的值。
师:类似地,你知道二元一次方程的解吗?
练习:试试寻找二元一次方程x+y=8的解
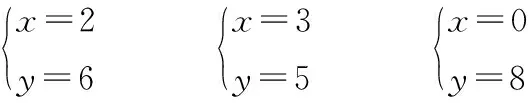

设计意图:此处设计由一元一次方程的解迁移到二元一次方程的解,目的在于让学生体会到可以类比一元一次方程的学习方法开展对二元一次方程的学习,渗透类比的数学思想。练习的设计目的在于说明二元一次方程的解由两个量(x,y)组成,并且通过取正数、负数、零、整数、分数等解顺应学生的心理特征,从而引导学生体会二元一次方程有无数组解。
4.请每位同学写出手上二元一次方程的几组解,并尝试找找一组x、y同时适合同桌两个方程(安排5分钟让学生同桌两人合作寻找公共解)。
设计意图:以学生的“学”为出发点,将“自主探究、合作交流”的学习方式贯穿于始终,从注重课堂整体性的高度,让学生作为课堂的主人充分体会合作学习的魅力,学会数学学习的方法,培养良好的情感态度价值观。
(三)整章预览,感悟数学思想,培养数学抽象素养
数学核心素养强调,只有用思维方法的分析带动具体知识内容的教学,才能真正帮助学生学好相关的数学知识。数学章起始课中的思想内涵是极为丰富的,我们不仅要重视知识和技能的传授,还要引导学生深度理解内容深层隐藏的数学思想方法和思维方法,渗透数学文化等隐性知识,为后续内容的学习打好基础、做好铺垫。
1.课堂小结
以表格的形式列出一元一次方程与二元一次方程的异同。你学到了哪些新知识?哪些数学思想方法?
设计意图:在课堂小结的环节意在在总结反思中,提高学生的学习效率,促进良好的数学学习习惯和方法的养成。首先,由学生自己对本节课所学知识进行归纳总结,在课堂展示后在通过师生共同评价修正,从而帮助学生建立整体性的认知框架,完善认知结构。其次,对课堂中出现的数学思想方法及时的进行总结提炼,使学生认识到数学思想方法在数学学习的中重要价值和作用,使得学生的数学认识上升到一个新的高度。
2.课后思考与作业
课后思考:根据课本103页老牛和小马的对话——
a.分别列出一元一次方程与二元一次方程组,再次体会两种方法妙处;
b.求出一元一次方程的解,观察是否适合二元一次方程组,并思考如何求方程组的解。
课后作业(其中①②题为必做题,③④题为选做题):
①在下列中,哪些是二元一次方程x-3y=1的解?

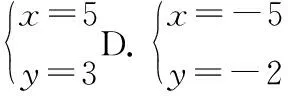
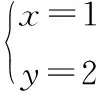
③若方程 2xm-1-3y2m+n=1 是二元一次方程,那么m=____,n=____.
④明从邮局买了面值50分和80分的邮票共9枚,花费6.3元,则小明买了两种邮票各几枚?
教学设计意图:针对学生的实际学情对教材做了大胆处理,把课前的情境引入放在课后思考让学生分别从一元一次方程和二元一次方程组的角度体会两种方式的妙处,并尝试把一元一次方程方程的解代入二元一次方程组,寻找两者之间的联系,同时为下一节课消元法解二元一次方程方程组埋下伏笔。
三、反思教学设计,深究课堂模式
本课例从方程的角度,二元一次方程是一元一次方程方程的深化和延伸,二元一次方程在一定程度上都可以转变成一元一次方程来解决。从函数的角度,二元一次方程可以看做是一种特殊的一次函数,二元一次方程的图形表示的是点的运动轨迹。而一次函数图像表示的是x,y通过图像的依赖关系。当两直线相交时对应二元一次方程组有唯一的解,当两直线平行时对应方程组无解,当两直线重合时对应方程组有无数组解。在教学过程中,应重视数学知识之间的关联性,通过知识间的关联性来培养学生举一反三的能力,逐步培养学生良好的数学思维能力,学会用数学思维分析问题和解决问题。
数学核心素养提倡高效的智慧课堂以学生的自主性、探究性、合作性学习为主体,师生共同合作实现教学目标。教学过程由“教”变为“导”,教师要放手教学,让学生大胆去编题、组题参与课堂学习。
总之,在教学中,教师要善于营造良好的学习氛围,激发学生的求知欲望,创造条件让学生充分参与学习活动,发挥学生自主能动性,要注意学生的学法指导,培养学生自主获取知识的能力,使学生学会知识、学会方法、提升能力以及培养良好情感价值观,只有这样,学生的自身数学素养才能得到更好的提高,才能让学生获取更主动的发展空间。
