基于最优边界划分的多层次复杂系统参数辨识方法 ①

孙玉涛， 司凤山， 崔 迪

(安徽财经大学 管理科学与工程学院，安徽 蚌埠 233000)

0 引 言

多层次复杂系统作为一种多元模糊控制系统，在进行多维度的参数控制中发挥重要作用，多层次复杂系统设计在航空航天以及机械二自由度控制等领域中具有重要应用价值。在进行多层次复杂系统设计中，对多层次复杂系统的参数辨识和优化估计是关键[1]，构建多层次复杂系统的参数辨识模型，采用空间物理参数寻优和收敛性设计方法，进行多层次复杂系统的优化控制设计，提高多层次复杂系统的控制性能，相关的多层次复杂系统控制方法研究受到人们的极大关注[2]。本文提出基于最优边界划分的多层次复杂系统参数辨识模型。构建多层次复杂系统参数辨识的约束参量模型，建立模糊控制函数进行多层次复杂系统参数的多层次复杂系统参数特征分解，结合小波函数多尺度分解方法进行多层次复杂系统参数特征量的多维分解，构建多层次复杂系统参数分量的特征重组模型，实现基于最优边界划分的多层次复杂系统参数辨识优化设计，最后进行仿真测试分析，得出有效性结论。

1 多层次复杂系统控制的约束参数和数学建模

1.1 多层次复杂系统控制的约束参数

为了实现多层次复杂系统参数辨识优化设计，提高多层次复杂系统的稳定性，需要进行多层次复杂系统，首先分析多层次复杂系统控制的约束参数模型[3]，采用模糊空间规划方法，进行多层次复杂系统的融合处理，进行多层次复杂系统控制参数寻优，采用二元微分方程建立多层次复杂系统参数辨识模型，结合二元多波束求解方法，分析多层次复杂系统参数映射f在I×R×R→R上的联系泛函，建立多层次复杂系统参数的空间规划模型，采用奇异值特征分解的方法，进行多层次复杂系统的模糊控制，构建多层次复杂系统参数分布特征量，得到二元微分方程为：

(1)

其中u:I×IRd→IR是多层次复杂系统参数分布的实值函数，d≥4。采用模糊逻辑分析方法进行多层次复杂系统参数辨识的专家系统模型设计[4]，得到多层次复杂系统参数分布的二元组合函数为：

Ψ(h1,h2)=Ψ+h1K(Z1+Z2+Z3)-1KT+

h2M(Z2+Z3)-1MT<0

(2)

结合二乘拟合，得到多层次复杂系统参数辨识的特征方程：

Ψ(h1,0)=Ψ+h1K(Z1+Z2+Z3)-1KT+

h2L(Z2+Z3)-1LT<0

(3)

结合分组线性映射，得到多层次复杂系统参数特征分解值满足：

f(x1,x2,i)-g(y1,y2,i)+

x(|x-y|2+x|x-y|2)

(4)

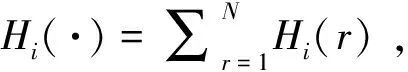
Co(x*)<0

(5)

采用多目标优化方法，求得多层次复杂系统参数辨识的半正定周期稳定解为：

(6)

如果Co(x*)=0，则多层次复杂系统参数分布特征量：

Y(P,Q,β)=Y[red(P,Q,β),Q,β]

(7)

多层次复杂系统参数的广义中心统计特征量分布矩阵满足：

Ψ1(d1(t))=Ψ+d1(t)K(Z1+Z2+Z3)-1KT+

(8)

由此构建多层次复杂系统控制的约束参数模型，采用模糊正交规划函数寻优方法，进行多层次复杂系统控制参数辨识和自适应寻优[5]。

1.2 多层次复杂系统控制数学模型

采用模糊二自由度微分方程进行多层次复杂系统参数辨识和多元规划模型设计，建立多层次复杂系统参数分析的模糊正交规划函数，基于Jacobi矩阵进行多层次复杂系统参数特征分析[6]，建立多层次复杂系统参数辨识模型表示为：

Ψ1(d1(t))=Ψ+d1(t)K(Z1+Z2+Z3)-1KT+

(9)

求解多层次复杂系统参数的稳定核，采用多复变微分方程进行多层次复杂系统参数稳定特征解为：

(10)

在无约束条件下，得到多层次复杂系统参数辨识的Jacobi控制函数，得到：

x(t)=φ(t)t∈[-h,0]

(11)

令xn+1=μxn(1-xn)是多层次复杂系统参数辨识的非线性特征方程，建立多层次复杂系统参数分析的模糊正交规划函数，结合模糊交叉控制方法进行多层次复杂系统参数的分布式拟合控制[7]，建立模糊控制函数进行多层次复杂系统参数的多层次复杂系统参数特征分解，对于适当维数的系统矩阵x=(x1,…,xm)T∈GF(2n)m，多层次复杂系统参数辨识的稀疏矩阵β=(β1,…,βm)T∈GF(2n)m，其中，n=1,2,3,…，x∈[0,1]，μ∈[0,4]，多层次复杂系统参数分布特征集A=(aij)m×m，aij∈GF(2n)，采用融合性分析方法，得到多层次复杂系统参数的统计分布集：

(12)

式中AT表示矩阵A的转置，结合模糊度控制方法，进行多层次复杂系统参数识别和二元规划设计，提高多层次复杂系统的输出稳定性。

2 多层次复杂系统参数辨识

2.1 多层次复杂系统参数特征分析

结合小波函数多尺度分解方法进行多层次复杂系统参数特征量的多维分解，构建多层次复杂系统参数分量的特征重组模型，记多层次复杂系统参数的约束参数为：

(13)

(14)

(15)

d=max{2A1,4A2}

(16)

采用边界性约束条件，用边界性约束条件，进行多层次复杂系统参数分析[8]，得到多层次复杂系统参数辨识的惯性特征量：

(17)

其中：

(18)

(19)

k1为多层次复杂系统参数的最大共轭梯度；k2为多层次复杂系统参数分布的连续泛函。

2.2 多层次复杂系统参数辨识输出

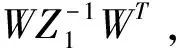
Ψ1(d1(t))=Ψ+d1(t)K(Z1+Z2+Z3)-1KT+

(20)

Ψ2(d2(t))=Ψ+(h2-d2(t))L(Z2+Z3)-1LT+

d2(t)MT(Z2+Z3)-1MT

(21)

在临界点(-1,0)处，得到多层次复杂系统参数辨识的空间分布如图1所示。

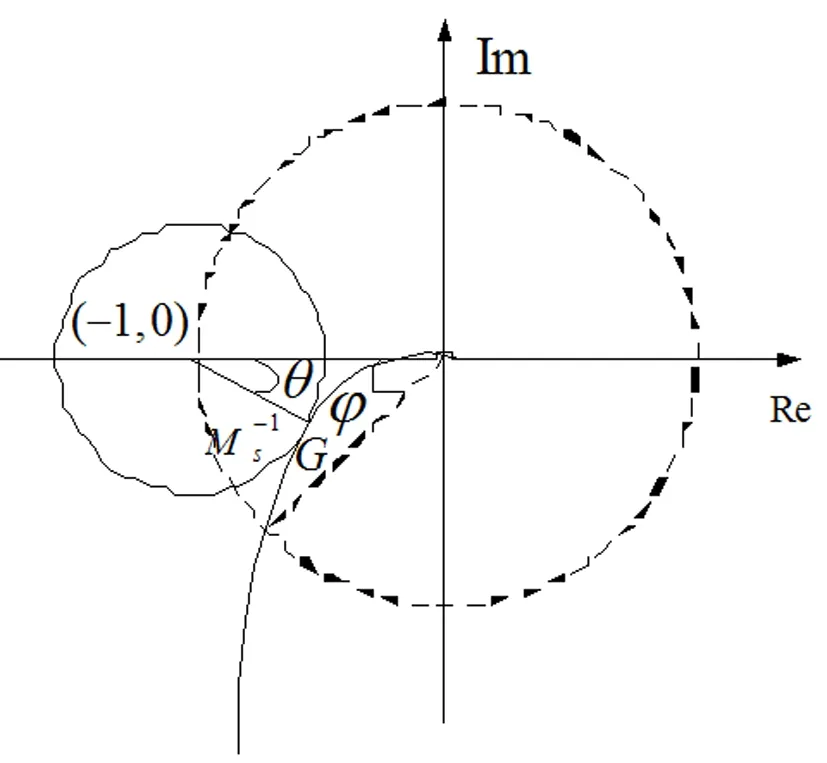
图1 多层次复杂系统参数辨识的空间分布

根据图1的参数空间分布，得到多层次复杂系统参数辨识的解析方程为：

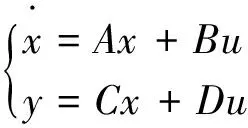
(22)

上述模型中：

(23)

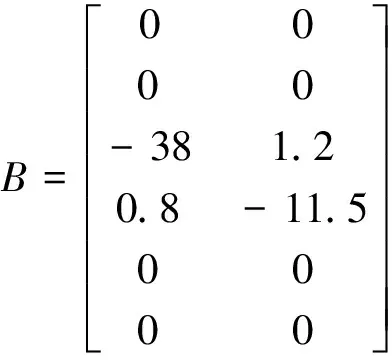
(24)

多层次复杂系统参数特征解x=[φ,ψ,P,r,v,ye]T，输出量u=[δa,δr]，综上分析，实现对多层次复杂系统参数辨识的优化设计，得到空间平衡点为：

(25)

采用二元回归分析方法，进行多层次复杂系统参数特征融合，建立多层次复杂系统参数统计分析模型[10]，得到统计特征量为：

(26)

p=-(fx1+gx2)|Pi,i=1,2,3,4

(27)

q=detA|Pi,i=1,2,3,4

(28)

综上分析，结合模糊正交规划函数的自动寻优方法进行多层次复杂系统参数的自适应求解，提高多层次复杂系统参数辨识的精度，实现多层次复杂系统参数辨识模型设计。

3 仿真实验分析

为了验证本文模型在实现多层次复杂系统参数辨识中的应用性能，进行实验测试分析，多层次复杂系统参数采集的节点数为12，边数为45，自适应学习的加权系数为0.35，收敛步长为50，根据上述仿真参数设定，进行控制参数辨识，得到参数辨识输出如图2所示。

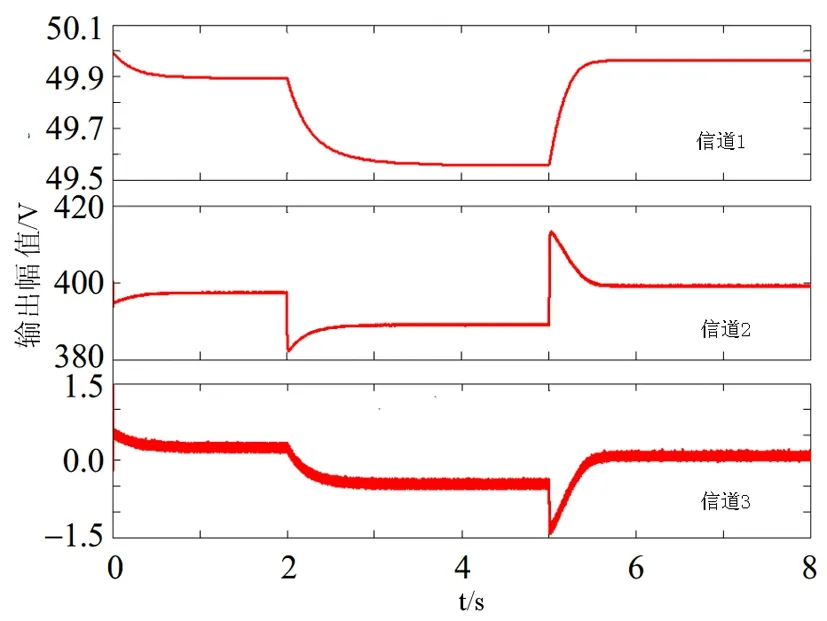
图2 参数辨识输出

分析图2得知，本文方法能有效实现多层次复杂系统参数辨识，测试收敛性，得到结果如图3所示，分析图3得知，本文方法进行多层次复杂系统参数辨识的收敛性较好。

图3 收敛性测试

测试参数辨识的控制精度，得到对比结果见表1，分析表1得知，本文方法进行多层次复杂系统参数辨识的辨识精度较高。

表1 不同算法辨识结果

4 结 语

本文提出基于最优边界划分的多层次复杂系统参数辨识模型。采用模糊逻辑分析方法进行多层次复杂系统参数辨识的专家系统模型设计，构建多层次复杂系统控制的约束参数模型，采用模糊正交规划函数寻优方法，进行多层次复杂系统控制参数辨识和自适应寻优。建立模糊控制函数进行多层次复杂系统参数的多层次复杂系统参数特征分解，结合模糊正交规划函数的自动寻优方法进行多层次复杂系统参数的自适应求解，提高多层次复杂系统参数辨识的精度，实现多层次复杂系统参数辨识模型设计。分析得知，采用本文方法进行多层次复杂系统参数辨识的收敛性较好，多层次复杂系统参数辨识的精度较高。