板厚对闸门结构自振频率的影响

李云中 吝江峰 李 涛

(1.昆山市水利设计院有限公司，江苏 昆山 215300；2.江苏省水利勘测设计研究院有限公司，江苏 南京 225009)

1 概 述

现有闸门规范中闸门结构按照平面体系考虑，实际工程闸门应该是一个完整的空间体系，作用外力和荷载将由全部的组件共同传递分担，因此，按平面体系计算闸门结构自振频率时，无论作多么精细的假定，总是不能完善地反映出闸门真实的工作情况。工程中常见门型，尤其是平面焊接闸门，其空间薄壁结构特征非常明显，在计算机软硬件很发达的当下，采用有限元分析作为平面体系计算的一个补充和印证，是值得推荐的一种设计工作方式[1-2]。

由于闸门系统各阶振动的广义质量、广义刚度、模态阻尼比和广义荷载都是不一样的，系统总响应中，来自各阶模态的“贡献量”也是不一样的。对于高阶模态，当来自它们的贡献已足够小时就可以忽略。所以一般有限元计算仅取前几阶频率来考察结构的振动特性。本文对平面闸门前三阶自振频率列出数据进行比较，并根据一阶自振数据绘制板厚—自振频率图形，以便直观反映板厚与自振频率的关系。

2 板厚对闸门结构自振频率影响理论推导

众所周知，自振频率是指弹性体或弹性系统自身固有的振动频率，又称“固有频率”。是弹性体或弹性系统的固有属性，其数值与初始条件和所受外力的大小无关。对于多质点体系，忽略阻尼影响吋，自振频率与自身质量及其分布(刚度)、边界支承条件以及振动型式(称为“振型”)有关。振型是对应于频率而言的，一个固有频率对应于一个振型。按照频率从低到高的排列，依次称为第一阶振型、第二阶振型等等，指的是在该固有频率下结构的振动形态，频率越高则振动周期越小。实际结构的振动形态并不是一个规则的形状，而是各阶振型相叠加的结果[3-4]。

闸门是一个多自由度系统，用刚度法来求解结构的自由振动频率和振型，首先要确立结构的动力微分方程。根据达朗贝尔原理，多自由度弹性结构的动力微分方程为

(1)

式中K、M、C——系统的刚度矩阵、质量矩阵和阻尼矩阵；

F——荷载向量。

一般结构系统的阻尼对自振频率和振型的影响很小，因此，一般在分析确定系统的自振频率和振型时不考虑式(1)的阻尼项，无阻尼系统的自由振动方程为

(2)

假定各质体做简谐振动，设其中一组特解为

y=Φsin(ωt+v)

(3)

Φ=[ψ1ψ2…ψn]

(4)

将式(1)及其二次微分代入式(2)并消去公因子sin(ωt+v)，得

(Kω2M)Φ=0

(5)

式(5)中Φ行列式为零时意味着各质点振幅为零，说系统各质点没有振动，此式没有意义。故得出

|Kω2M|=0

(6)

展开式(6)这个行列式，将得到以ω2为未知数的代数方程，求解这个一元n次方程，从而求出n个频率ω1，ω2…ωn。这些频率由小到大的次序排列即构成频率谱。其中最小的称为最低自振频率，也称为基本频率。其余为高阶频率。

由式(6)不难看出，质体矩阵是结构的物理特性，对于一个确定结构其质体矩阵是确定的。那么ω2与K(刚度矩阵)成正比，即结构的刚度大则其自振频率高。

3 结构模型

根据工程基础资料，建立闸门三维参数化模型(见图1)。

图1 闸门参数化模型

4 边界条件

水工闸门出现振动现象的诱发因素很多[5]，主要两个方面，即外部因素和内部因素。外部因素包括水流的波动、水流的扰动、启闭及牵引设备作用力的脉动等；内部因素包括闸门的自振频率、闸门的支撑型式、止水的布置形式等。而对于闸门的自振频率而言，除了自身的结构型式、质量分布、构件连接型式影响自振频率外，边界条件是影响自振频率和振型的重要因素。本文算例闸门基于两个假设，第一，构件的焊接连接为全焊透，即假设闸门为薄壁空间结构，二，假设闸门搁置在底坎上且闸门的滚轮支撑装配不参与自振频率的计算，即闸门自振频率计算时边界约束条件简化为门叶边梁主轴孔铰轴约束，门叶底缘为垂直方向的单向约束。

闸门有限元模型见图2。

图2 闸门有限元网格化模型

5 动力分析

一般情况下平板闸门的面板质量在结构自重中的权重比较大，故分两种情况对板厚与自振频率的影响进行有限元分析。

a.面板厚度等差变化，其他构件板厚不变。结果见表1、图3。

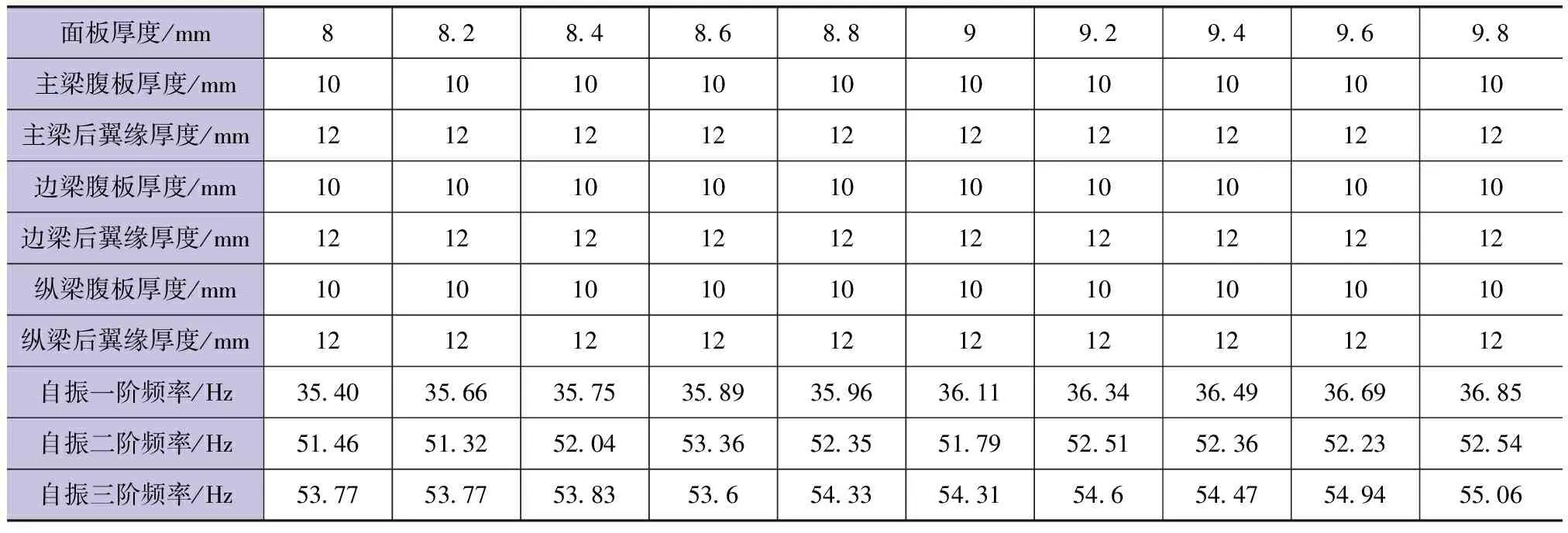
表1 有限元分析(一)

图3 自振频率—面板厚度曲线

b.各构件板厚等差变化。结果见表2、图4。

表2 有限元分析(二)

续表

图4 自振频率—各构件厚度曲线

6 结 论

根据理论推导，闸门各构件板厚的变化影响闸门刚度变化，闸门自振频率的平方与刚度成正比。

通过改变各构件板厚，进行多次闸门结构自振频率有限元分析后得出以下结论：随着构件板厚增加，相同约束条件下自振频率会增加。与理论推导结果一致，即刚度增加，结构的自振频率随之增加；闸门结构的板厚增加，闸门结构的刚度随之增加。但对于闸门这样的薄壁空间结构，板厚等差线性增加，各构件板厚对刚度增加的贡献是非线性的，故自振频率与板厚线性关系不明确，但两者函数关系的单调性明显；由于闸门防腐或因腐蚀等因素引起的板厚变化对闸门结构的自振频率是有影响的。面板厚度的变化对结构整体的自振频率影响明显，闸门各构件钢板厚度等差增加，频率升高显著。

鉴于以上结论，闸门在进行自振频率分析时应以结构的实测板厚作为计算依据，否则，其自振频率的分析结果跟实际情况会存在很大偏差。