基于Mann-Kendall法和重标极差法对大渡河毛头码站降雨趋势的分析
2021-01-13李燐楷,李文锦,陈志峰,陈坚,顾晓
李 燐 楷, 李 文 锦, 陈 志 峰, 陈 坚, 顾 晓
(中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081)
0 引 言
Mann-Kendall 法是一种基于秩次非参数统计检验方法,由于该法对统计样本所服从的分布无特别要求,且对少数异常值不敏感,在判断降水、径流、气温等时间序列中长期变化趋势方面应用广泛,是世界气象组织推荐并已广泛使用的非参数检验方法[1]。重标极差法是分形理论中的一种重要研究方法,在研究自然界某些随机且具有相似性的现象(如降雨、径流、洪水等)中有着广泛的应用,同时在社会科学和工程领域(如股票及汇率的波动等)有巨大的应用潜力[2]。英国水文学家赫斯特(H.E.Hurst)于1965年首次尝试将径流时间序列作为时间分形结构,采用重标极差法分析其时间尺度上的相似性。重标极差法已在暴雨时空分布、径流序列趋势等方面广泛应用[3]。
毛头码水文站位于大渡河下游干流,距支流尼日河汇聚口2.7 km,控制流域面积7.27万km2,自1964年开始进行降雨观测以来,流域气候条件变化相对稳定,但受全球气候变暖和大气环流等大尺度影响因子变化的影响,流域降雨量趋势呈现相应的变化。本文采用Mann-Kendall法重标极差法和重标极差法对大渡河毛头码站降雨序列进行趋势分析,用Mann-Kendall法分析降雨系列的总体趋势,以重标极差法分析降水系列在时间尺度上的分形特征,判断降雨序列的未来趋势。
1 重标极差法和Mann-Kendall法综合分析
1.1 重标极差法
一般地,对于降雨时间序列pt(t=1,2,…,n),重标极差法分析步骤如下[4]:
(1)将降雨序列Pt(t=1,2,…,n)等分成长度为τ的m个连续子序列,其中τ为整数,取值范围2≤τ≤n/2且Mτ≤n。各子序列记为Dm(m=1,2…M),序列Dm包含τ个元素,记为pk,m(k=1,2,…τ)。
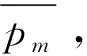
(1)
(3)由子序列Dm的累计离差最大值减去最小值记为Dm的极差记为Rm,其标准差为Sm:
Rm=maxPτ,m-minPτ,m
(2)
(3)
(4)分段长度为m时,M个子序列Dm的(Rm/Sm)均值,即为
(4)
(5)对于序列重构后,子序列长度τ与Hurst系数及重标极差的关系为:(R/S)τ=(cτ)H,两边取对数可得:lg(R/S)τ=Hlgc+Hlgτ,常采用最小二乘法估算在不同序列长度τ下Hurst系数的取值。
年降雨序列在大时间尺度下会表现周期性和趋势性的特点,但由于受大气环境和地形地貌等多种因素影响,其周期性和趋势性并不显著,利用重标极差法可有效剔除噪声对时间序列周期性和趋势性的影响。一般的,赫斯特系数H取值不同表示序列趋势的持续性不同:当H=0.5时,表示时间序列前后完全独立,具有随机游走的特性;当H>0.5时,表示序列具有长程相关性,未来变化趋势与过去一致,H值越接近1表示持续性越强; 当H<0.5时,表示序列具有反持续性,未来变化趋势与过去相反,H值越小反持续性就越强,在这种情况下,过去的增加趋势预示着未来的减少趋势,而过去的减少趋势则使未来可能出现增加趋势[5]。
赫斯特系数显著性检验利用R/S的期望公式估算序列的经验值,并用最小二乘原理估算系列的斜率E(H),E(H)服从正态分布,且方差为Var(E(H)τ)=1/N,采用U检验对实际Hurst系数进行显著性检验,在置信区间取95%时,U0.05临界值为1.96。R/S期望值经验公式如下[6]。
E(R/S)τ=((τ-0.5)/τ)·(τπ/2)-0.5·
(5)
1.2 Mann-Kendall秩次非参数检验
对降雨序列降雨时间序列pt(t=1,2,…,n),n为系列长度,其统计值Z的计算公式为:
(6)
其中M为对偶系列的个数,计算公式为:
(7)
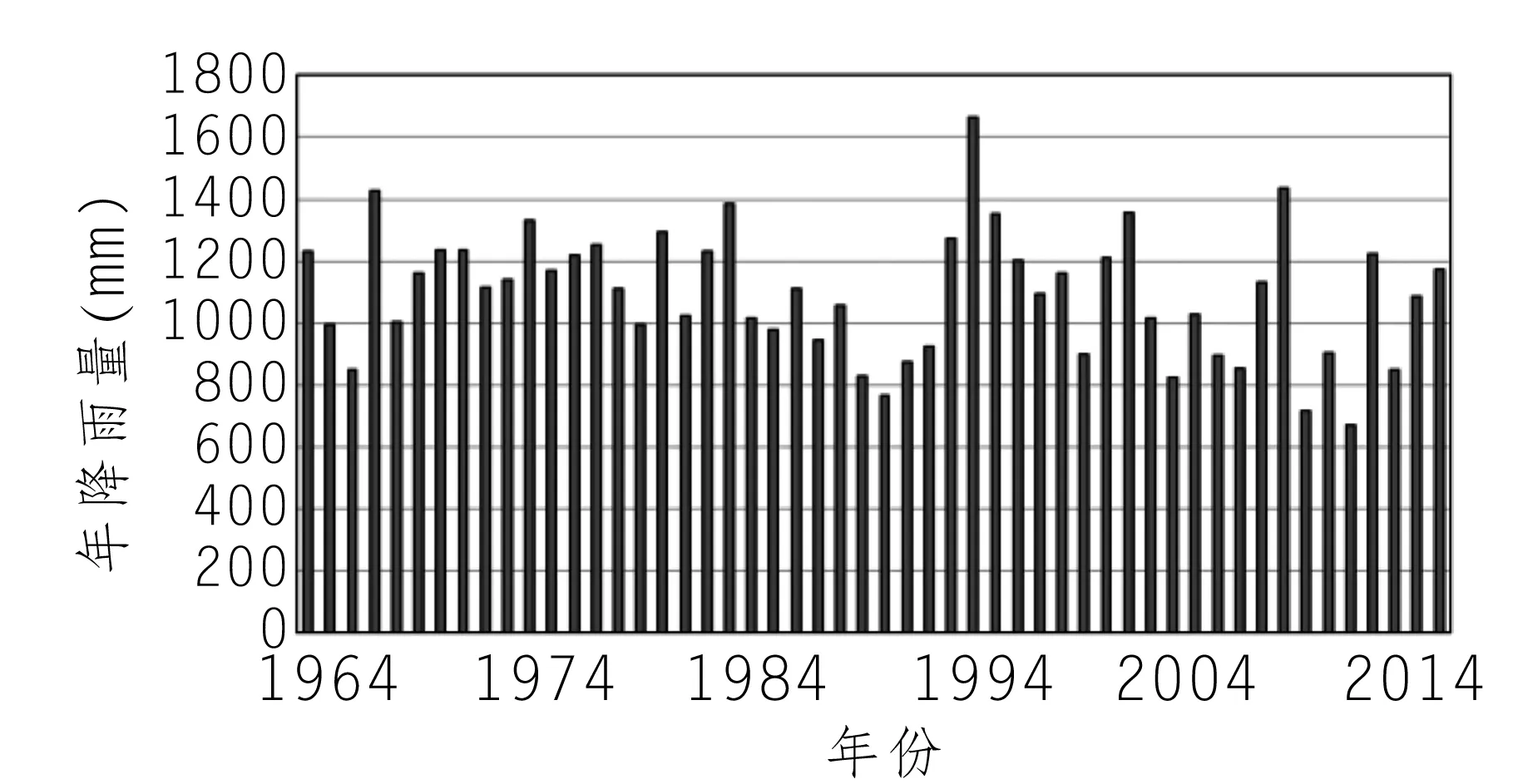
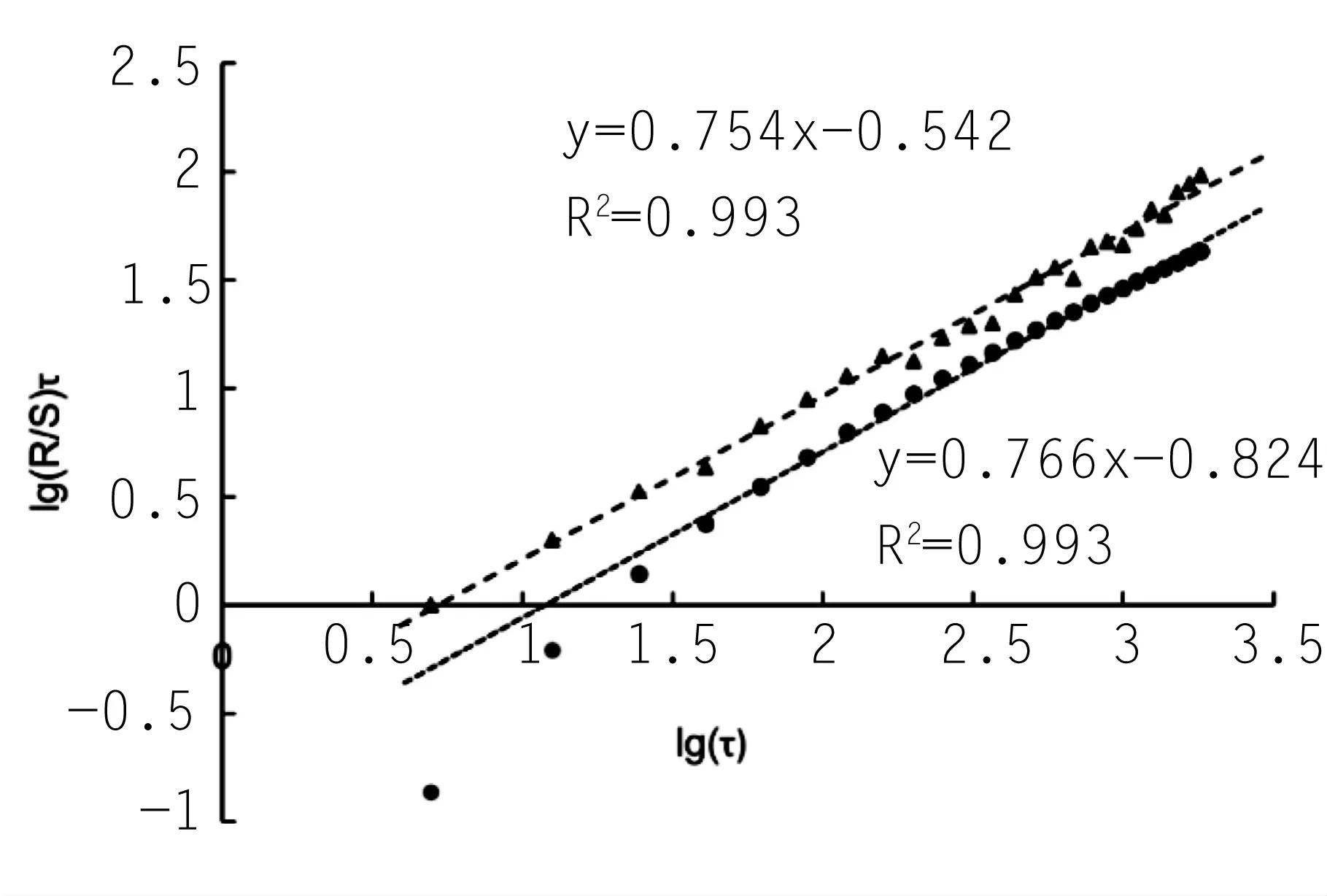
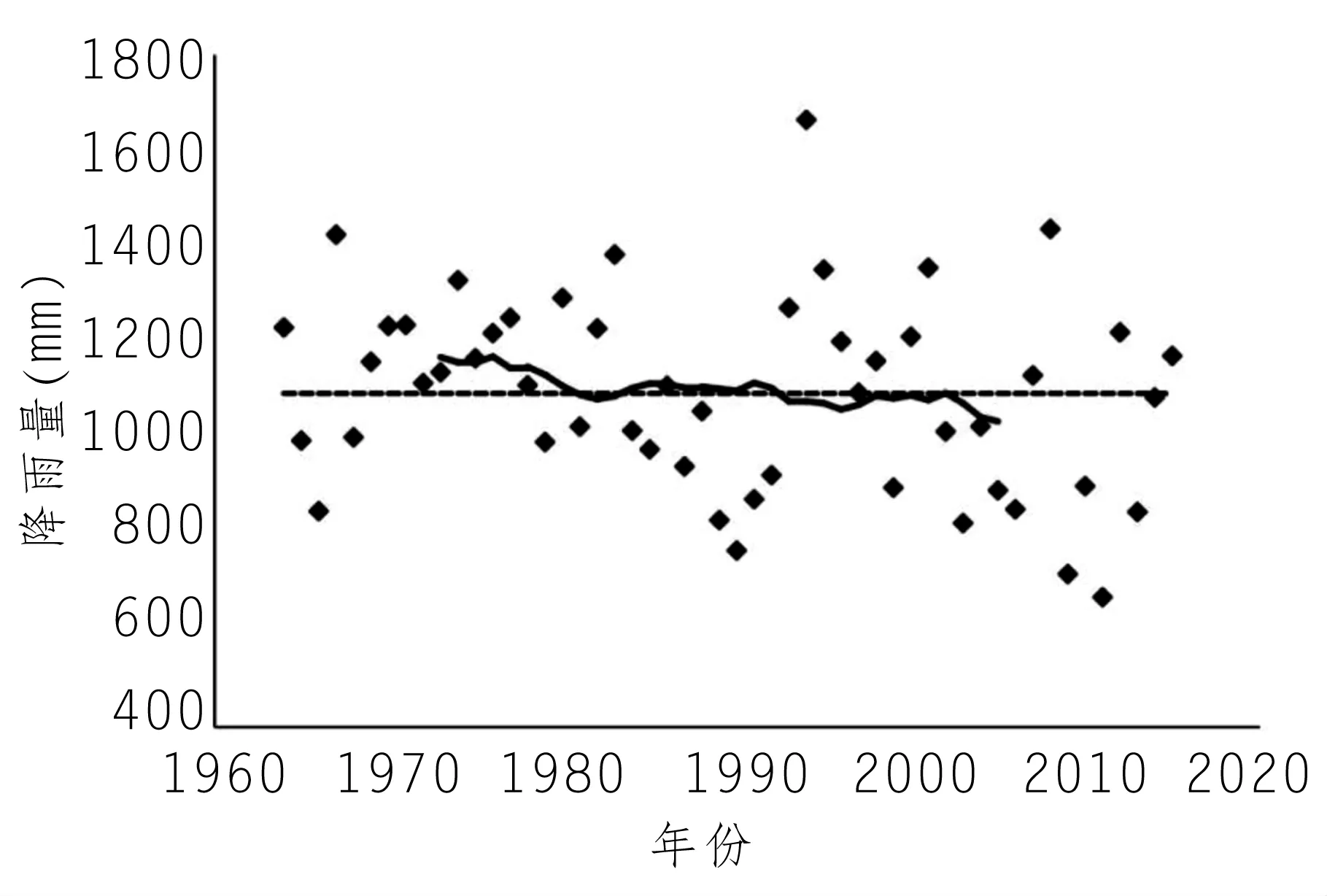
Var(s)为标准差,估算公式为Var(s)=n·(n-1)·(2n+5)/18,若统计量Z>0,表示序列具有上升的趋势,若Z<0,表示序列具有下降的趋势,给定置信水平a,若|Z|≥Z1-α/2,表示趋势显著,若|Z| 1.96、2.58[7]。 将Mann-Kendall法与重标极差法相结合,先通过Mann-Kendall法判断序列的上升或下降的趋势,并检验其趋势的显著性,而后采用重标极差法计算序列的Hurst系数,判断序列的趋势在未来的持续性[8],判断方式见表1。 表1. Hurst系数与Mann-Kendall法对序列趋势综合判断表 大渡河毛头码水文站是国家一级水文监测站,是大渡河流域水文观测的重要控制站,其降雨序列也是本地区及下游水利水电工程的重要参考[9],本文收集毛头码水文站1964-2015年共52年降雨序列,采用重标极差法分析降雨序列的Hurst系数,判断系列变异点和序列趋势的持续性,采用Mann-Kendall法检验系列的趋势及显著性,并结合上述两种方法的成果,判断大渡河毛头码站未来降雨的趋势。图1为大渡河毛头码站1964~2015年降雨序列。 图1 大渡河毛头码站年降雨量序列 采用重标极差法对毛头码站52年降雨数据进行分析,分段时长τ取值为2,3……26,按重标极差分析步骤依此计算不同分段时长τ时的R/S均值(R/S)τ,并对(R/S)τ和τ取对数,得lg(τ)和lg(R/S)τ序列,采用Hurst系数期望公式计算R/S的期望值对数lg(E(R/S)τ)和Vτ,分别用于求赫斯特系数的期望值E(H)和检验序列的平均周期。作lg (R/S)τ与lg(τ),和lg(E(R/S)τ)与lg(τ)的关系图(见图2)。 图2 实际与理论lg(R/S)τ-lg(τ)关系图 由图2可知,大渡河毛头码站1964-2015年降雨序列在分段长度为2≤τ≤26时,lg (R/S)τ与lg(τ)拟合直线较好,无明显拐点,此时拟合直线斜率即Hurst系数为0.754,lg(E(R/S)τ)与lg(τ)点系列拟合直线斜率为0.766,采用U检验对降雨系列的Hurst系数和由lg(E(R/S)τ)-lg(τ)点拟合的期望值E(H)进行显著性检验(表2),由表可知无显著差异。降雨序列Hurst系数大于0.5,且无明显变异点,表明大渡河毛头码站降雨序列具有长期相关性,未来趋势将保持一致。 表2 毛头码水文站降雨序列赫斯特系数及检验结果 利用Mann-kendall法对该降雨序列进行趋势分析,可知其统计参数Z=-1.95小于零,且|Z|≥Z1-α/2,其中置信水平为90%,Z1-α/2=1.65,表明降雨序列在90%的置信水平下,具有显著下降趋势。采用滑动平均法对趋势检验成果进行验证,滑动平均法的基本公式为:Pt= 表3 Hurst系数与Mann-Kendall法对序列趋势综合判断表 图3 毛头码站降雨量均值及20年滑动平均值对比图 由表3可知,采用重标极差法计算大渡河毛头码站降雨序列Hurst系数,H为0.754,H>0.5且与E(H)无显著差异,表明序列具有长期持续性;采用Mann-Kendall法,大渡河毛头码站降雨系列统计参数Z为-1.95,|Z|>Z0.10,表明毛头码站降雨呈显著的下降趋势,与滑动平均值结论一致;综合重标极差法与Mann-Kendall法分析结果可知,大渡河毛头码水文站1964-2015年降雨序列呈下降趋势,且这种下降的趋势在未来具有持续性,即未来降雨量还会继续表现为下降。 本文采用重标极差法和Mann-Kendall法对大渡河毛头码站1964-2015年降雨序列进行分析,重标极差分析结果表明:该序列lg(R/S)τ-lg(τ)序列点相关性较好,无明显突变点,且Hurst系数与其期望值较为接近,无显著差异,表明序列的趋势具有较强的持续性;Mann-Kendall法分析结果表明,降雨序列在90%的置信水平下,具有显著的下降趋势,且与滑动平均法结果一致。 综合重标极差法和Mann-Kendall法分析结果可知,大渡河毛头码水文站降雨量的下降趋势具有较强的持续性,从1964-2015年共52年的观测期来看,该站年降雨量具有下降趋势。大渡河毛头码水文站降雨序列未来持续减少的趋势,可能跟全球气候变暖及内陆水汽持续减弱有关,其具体原因需进一步研究,但本综合法为降雨或径流等随机性较强的时间序列趋势预测提供了一种分析工具,具有重要的实用价值。1.3 综合分析

2 应用实例

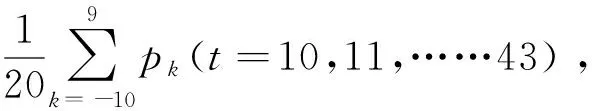

3 结 语
